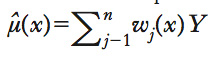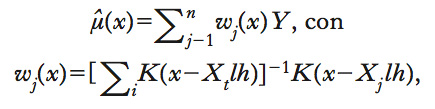regressione non parametrica, modelli di

regressione non parametrica, modelli di

Modelli di regressione (➔ regressione, modelli e stimatori di) che hanno come oggetto di interesse una caratteristica della distribuzione condizionata di una variabile dipendente Y (➔ dipendente, variabile) dato un insieme di regressori X, per es. la media condizionata μ(x)=E(Y∣X=x) (➔ media). Tali modelli sono utilizzati quando si vogliono limitare al massimo le assunzioni circa la distribuzione condizionata di Y dato X (➔ distribuzione di probabilità). Per la natura stessa dell’analisi di r. n. p, che non impone restrizioni sulla forma funzionale di μ(x), si può dire che è il metodo di stima che induce il modello n. p., e non viceversa. Tra i principali stimatori n. p., si limiterà l’analisi al caso di un modello per la media condizionata. Si assuma perciò di disporre di un campione casuale {(Y₁,X₁),...,(Y_n,X_n)} (➔ campione statistico) e di essere interessati alla stima della funzione μ(x)=E(Y∣X=x) che descrive il comportamento della media condizionata di Y, dove X può indicare un unico regressore o un insieme di K regressori. Gran parte degli stimatori più comunemente usati possono essere scritti come funzioni lineari dei valori osservati di Y, (Y₁,...,Y_n), cioè come

dove i pesi w_i(x) dipendono soltanto dalle X_i e da x. Il vantaggio principale della linearità è la semplicità, che rende possibile calcolare le proprietà statistiche degli stimatori stessi (➔ stimatore). Inoltre, la comune struttura lineare rende possibile il confronto tra le proprietà di stimatori anche molto diversi tra loro attraverso il confronto dei diversi sistemi di pesi. Stimatori di questo tipo sono anche chiamati lisciatori lineari di r. (linear regression smoothers), dove per lisciatore di r. si intende una qualsiasi funzione dei dati tramite la quale si possono ottenere valori predetti μ ̂(X_i) che sono più ‘regolari’ dei valori Y_i osservati.

Principali lisciatori lineari di regressione

Uno spline di regressione approssima la funzione attraverso una funzione polinomiale (tipicamente lineare, quadratica o cubica) a tratti. Il tipo più semplice è lo spline lineare: una volta suddiviso l’insieme dei valori di Y in intervalli adiacenti, si calcola in ciascun intervallo la retta che approssima meglio la funzione μ(x) sotto il vincolo che quella risultante sia continua. Uno dei punti critici di tale procedura consiste nella scelta del numero di intervalli e della loro posizione. ● La stima kernel di regressione è un metodo basato sul calcolo della media condizionata attraverso l’uso di una stima di tipo kernel della densità condizionata f(y∣x) (➔ kernel density). Un caso particolare è lo stimatore di Nadaraya-Watson, che può essere scritto nella forma

dove K è una funzione kernel e h è l’ampiezza di banda (bandwidth). ● Il metodo del vicino più prossimo (nearest neighbor). Per ogni valore x, si ricavano i valori X_i più vicini a x e si stima μ(x) come media dei corrispondenti valori di Y. Nel caso in cui si prendano i K valori più vicini a x, si ha lo stimatore μ ̂(x)=Σ_jw_j(x)Y_j, dove w_j(x)=1/K se X_j è tra le K osservazioni più vicine a x, e, altrimenti, w_j(x)=0. In altre parole, si tratta di una media mobile di valori di Y (➔ destagionalizzazione). ● Una versione più sofisticata di approssimare localmente μ(x) con una media mobile usa un’approssimazione localmente lineare, cioè, per ogni x, si assume

dove i coefficienti α(x) e β(x) sono stimati usando le osservazioni corrispondenti ai valori X_i più vicini a x. Tutti gli stimatori sopra citati possono essere ricavati minimizzando la somma ponderata dei quadrati Σ_jw_j(x,X₁,...,X_n)(Y_j−c_j)² rispetto a c=(c₁,...c_n), dove c dipende soltanto da (X₁,...,X_n) ma non da Y. Ciò che cambia tra i diversi metodi sono i pesi w. Si noti che lo stimatore dei MQO, minimi quadrati ordinari (➔ minimi quadrati, metodo dei), pur essendo uno stimatore parametrico, può essere visto come un caso particolare, corrispondente al caso w_i=1/n e c_i=α+βX_i. ● Il problema principale degli stimatori n. p. è noto con il nome di ‘maledizione della dimensionalità’ (curse of dimensionality): le proprietà asintotiche (➔ asintotica, distribuzione) di tali stimatori peggiorano all’aumentare del numero K di regressori, e il peggioramento è più che proporzionale all’aumento di K.

Metodi semiparametrici

Un’alternativa è costituita dai metodi semiparametrici, che costituiscono un compromesso tra la flessibilità di un modello n. p. e la semplicità e l’efficienza nella stima di un modello parametrico. Tali modelli si basano su una parte puramente n. p., e una parte parametrica, che generalmente è inserita al fine di ridurre la dimensione K delle variabili in μ(X_i,...X_k), eliminando così il problema della maledizione della dimensionalità. Un esempio di stimatore semiparametrico è lo stimatore single-index, in cui la funzione μ prende la forma di una funzione a un solo argomento μ(X₁,...,X_k)=g(β₁X₁+...+ β_kX_k), dove β₁,...,β_k sono parametri ignoti e g è una funzione ignota.