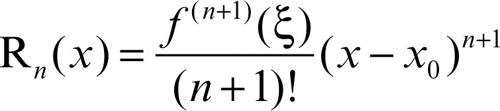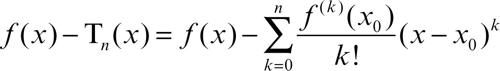Lagrange, resto di

Lagrange, resto di

Lagrange, resto di espressione del resto della formula di → Taylor della forma

con ξ opportuno valore dell’intervallo (x₀, x). Il resto R_n(x) è la differenza

tra la funzione e il suo polinomio di Taylor di grado n. La validità della formula è assicurata se ƒ è dotata di derivate continue fino all’ordine n nell’intervallo chiuso [x₀, x] ed esiste la derivata di ordine n + 1 nell’intervallo aperto (x₀, x). Questa espressione del resto è importante perché consente una stima dell’errore commesso sostituendo a ƒ(x) il polinomio di Taylor: infatti se in (x₀, x) risulta |ƒ ⁽ⁿ⁺¹⁾(ξ)| ≤ M, sarà anche |R_n(x)| ≤ M|x − x₀|ⁿ⁺¹/(n + 1)!. Una tale maggiorazione, tuttavia, è di solito possibile (per il teorema di Weierstrass) se ƒ ⁽ⁿ⁺¹⁾ è continua in [x, x₀]. Un’altra applicazione del resto di Lagrange si ha quando il segno di ƒ ⁽ⁿ⁺¹⁾ è noto in un intorno di x₀: è allora possibile determinare il segno del resto a sinistra e a destra di x₀, stabilendo così se il grafico della funzione attraversa o meno quello del suo polinomio di Taylor. Per esempio, la funzione ƒ(x) = sin(x ^5/3) non è dotata di derivata seconda nell’origine, dove ammette un flesso, perché la derivata seconda ƒ″ (x) = (10/9x^−1/3)cos(x ^5/3) − (25/9x ^4/3)sin(x ^5/3) cambia segno (il fattore x^−1/3, infinito, moltiplicato per una funzione positiva in un intorno dell’origine, prevale sull’altro).