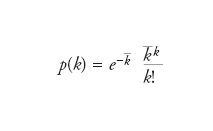rete neurale ricorrente
rete neurale ricorrente
Tipo peculiare di rete neurale artificiale che, oltre alle vie di connessione ascendenti, possegga anche quelle discendenti o ricorrenti, ossia, che connetta le unità di output con quelle intermedie e con quelle di input. Queste connessioni addizionali producono una rete la cui risposta vettoriale (nello strato intermedio) all’input dello strato sensoriale è in parte una funzione del concomitante stato di attivazione (o cognitivo) del terzo strato il quale, a sua volta, è la risultante di input ed elaborazione precedenti. Una risposta ricorrente della rete a un determinato stimolo, quindi, non viene fissata soltanto dai caratteri strutturali della rete stessa, come si verifica nella rete feedforward. La risposta varia come funzione del precedente contesto dinamico o cognitivo in cui si è manifestato lo stimolo. Per un sistema ricorrente di questo tipo, la risposta dello strato intermedio si manifesta come una sequenza di vettori di attivazione. Ogni rete ricorrente rappresenta una forma di memoria a breve termine: le informazioni raccolte nel vettore di attivazione dello strato intermedio vengono elaborate nello strato successivo e, quindi, rinviate alla propria origine, forse in forma modificata. Tali informazioni possono muoversi più volte lungo questo anello ricorrente, attenuandosi gradualmente. Se alcune informazioni sono importanti, la rete può anche avere una configurazione capace di conservarle senza attenuazione attraverso molti cicli, fino a che il contesto cognitivo non la ritenga più utile. Questo sistema fornisce automaticamente una forma di memoria a breve termine, sensibile al contenuto, con un tempo variabile di decadimento. Una rete ricorrente è altresì in grado di impegnarsi in un’attività cognitiva anche in assenza di una stimolazione in arrivo allo strato di input, perché gli impulsi che viaggiano sulle vie ricorrenti possono essere sufficienti a mantenere il sistema in attività. Essa può modulare inoltre, per mezzo di quelle stesse vie, la modalità di reazione agli stimoli dello strato sensoriale, e la salienza di taluni aspetti di quell’input. (*) → Neurofilosofia
reti di Erdos-Renyi [MAT] Un grafo è caratterizzato da una serie di punti, chiamati vertici, connessi da linee. Essi costituiscono entità astratte che possono però rappresentare diversi aspetti della nostra realtà. I vertici potrebbero essere, per es., delle città mentre le linee le strade che le congiungono, oppure potrebbero essere personaggi che esercitano una particolare attività professionale e le linee un legame corrispondente ai rapporti di lavoro svolti in collaborazione. Nelle cellule sono presenti geni e proteine reciprocamente interconnessi in modo tale da far emergere una rete di unità il cui studio potrebbe essere affrontato, in linea di principio, con i metodi che sono familiari a chi si occupa di cinetica chimica. In questo caso le indagini sul comportamento di una rete forniscono sia il controllo dei flussi energetici sia quello della produzione dei componenti cellulari che entrano nel metabolismo. L’applicazione delle reti ha acquistato rilevanza anche nello studio delle comunicazioni (Internet), della linguistica, dell’ecologia, della diffusione delle epidemie. Purtroppo la loro complessità rende difficile il loro studio per cui è opportuno elaborare un’adeguata strategia valida per trattare architetture costituite da insiemi di nodi, ciascuno connesso attraverso k legami con gli altri. Il problema che si deve affrontare riguarda la distribuzione delle connessioni presenti espresse dalla probabilità p(k) che un nodo scelto a caso abbia k interconnessioni. La prima trattazione matematica di tale problema è stata formulata da Paul Erdös e Alfréd Rényi i quali hanno assunto che la distribuzione dei vertici sia del tutto casuale con tutti i nodi accessibili e che il loro numero rimanga inalterato durante l’intera vita della rete. Inoltre si assume che i vertici siano equivalenti e si uniscono con uguale probabilità agli altri. Si dimostra allora che per queste reti casuali vale la legge di distribuzione di Poisson, in base alla quale:
dove k è il numero di interconnessioni che escono da un nodo e k_ il numero medio di legami (scala della rete). Per valori elevati di k_ tale relazione tende ad assumere un andamento gaussiano.