reti neurali

reti neurali

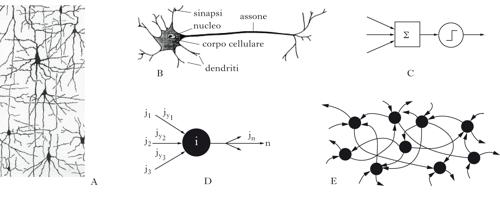
Le reti neurali sono modelli matematici definiti da molte semplici unità di elaborazione (neuroni), connesse tra loro (sinapsi); le modificazioni delle sinapsi determinano la capacità della rete di svolgere una computazione specifica (apprendimento). Identificando sottoinsiemi di neuroni come input (direttamente influenzati dall’ambiente esterno) e come output della rete, questa può realizzare specifici insiemi di corrispondenze input-output (regole) attraverso una procedura di apprendimento. I termini usati suggeriscono che in questo tipo di reti le proprietà dei nodi (neuroni) e dei link (sinapsi) sono definite in analogia alle loro controparti biologiche. Di fatto le reti neurali si sono evolute nel tempo in modo sempre più indipendente dalla metafora biologica, e sono diventate strumenti standard usati in problemi di statistica multivariata, di riconoscimento di pattern e di machine learning in generale. [➔ cervello, modelli per l’attività su larga scala; informazione neurale; intelligenza; intelligenza artificiale; neuroni e sinapsi, modelli teorici di] Le r. n. traggono originariamente il loro nome dall’idea che ci si possa ispirare alle strategie di elaborazione dell’informazione nel cervello e alle sue capacità di apprendimento per progettare dispositivi intelligenti (➔ intelligenza). Fra tali elementi di ispirazione, sono particolarmente rilevanti la natura stereotipata e universale dell’impulso nervoso e la plasticità sinaptica, che si ritiene sottesa alle capacità di memoria e di apprendimento del cervello. La possibilità di dotare una generica rete neurale di proprietà computazionali specifiche dipende dalla disponibilità di opportune strategie di apprendimento; verranno qui considerate solo modalità di apprendimento supervisionato, in cui le modificazioni sinaptiche dipendono dal feedback che la rete riceve dall’esterno, nella forma di un segnale di errore. L’apprendimento procede iterativamente sulla base di esempi di addestramento; la sua efficacia dipende dalla capacità della rete di generalizzare la regola appresa a nuovi esempi.

Il perceptron: imparare una regola da esempi

La natura ‘tutto o nulla’ del potenziale d’azione neuronale e il processo a soglia che ne governa la generazione (➔ neuroni e sinapsi, modelli teorici), suggerì molto presto una descrizione formale in cui il neurone è un dispositivo binario a soglia; nella rete, esso assume uno dei due stati permessi a seconda che la somma dei suoi input (da altri neuroni della rete), pesati dai ‘pesi sinaptici’, superi o meno una soglia assegnata. Una pietra miliare nella comprensione delle capacità computazionali di una tale rete binaria fu l’articolo A logical calculus of ideas immanent in nervous activity di Warren S. McCulloch e Walter Pitts (1943), in cui se ne dimostrava l’equivalenza con un automa universale (questo lavoro precedeva di diversi anni la comprensione del meccanismo di generazione del potenziale d’azione). Oltre alla valenza concettuale dei risultati generali ricavati nel lavoro citato e nei suoi sviluppi, l’interesse e il fascino di questo tipo di modelli erano naturalmente legati alla possibilità di definire procedure di ‘apprendimento’ in grado di dotare la rete delle proprietà computazionali desiderate. Fondamentale, per il ruolo storico e per la rilevanza concettuale, fu la formulazione del perceptron di Frank Rosenblatt, negli anni Cinquanta del 20° sec.: un insieme di input (binari o meno), collegati tutti a un neurone di output binario (del tipo del neurone di McCulloch-Pitts), ognuno mediante un peso sinaptico; il neurone di output effettua una somma degli input, pesata dai corrispondenti pesi sinaptici, la confronta con una soglia e fornisce a sua volta una risposta binaria. L’apprendimento consiste in una procedura iterativa che agisce sui pesi sinaptici: per ogni ‘esempio’ della regola, cioè una coppia insieme di valori di input/stato binario di output, se l’output fornito dal perceptron è corretto non si effettua nessun cambiamento sinaptico, altrimenti si cambia ogni peso sinaptico che connette un input attivo per quell’esempio, diminuendo o incrementando il suo valore a seconda che l’output sia erroneamente attivo o inattivo, rispettivamente. La regola di apprendimento risultò attraente per la sua semplicità, e anche perché fu possibile dimostrare un teorema di convergenza, dimostrare cioè che se una regola può essere imparata da un perceptron, la procedura iterativa descritta porta certamente a una configurazione dei pesi sinaptici che realizza la corrispondenza input-output prescritta dalla regola. Si noti l’originalità e il potere evocativo di una tale forma di apprendimento, che si realizza attraverso una serie di esempi di una regola. Sicuramente essa richiama alla mente molte forme di apprendimento che fanno parte dell’esperienza umana: un bambino impara la lingua madre per imitazione (quindi attraverso esempi) e non certo attraverso la definizione procedurale delle strutture linguistiche. Questo apre subito una questione a cui sarà data risposta più avanti: se la procedura di apprendimento ha prodotto una rete che fornisce la risposta giusta sugli esempi utilizzati, e ne ‘congeliamo’ la struttura, sarà in grado la rete di operare correttamente su nuovi esempi della stessa regola? In altre parole, sarà in grado di generalizzare? Un altro elemento che emerge è che la procedura di apprendimento richiede un supervisore: un agente esterno che valuta, per ogni esempio, la correttezza della risposta della rete e modifica i pesi sinaptici in modo da ridurre l’errore compiuto sugli esempi della regola. In qualche misura anche la natura supervisionata dell’apprendimento evoca analogie con elementi di esperienza comune, dato che l’interazione con l’ambiente contribuisce ad assegnare un valore alle nostre risposte, e a guidare il nostro apprendimento: il bambino di cui sopra è spinto a correggere il proprio uso della lingua a seconda che i suoni articolati riproducano o meno quelli ascoltati, e che essi siano o non siano correttamente compresi. L’analogia ha dei limiti: l’ambiente esterno non ha accesso alle nostre sinapsi: se anche nella r. n. biologica, come in effetti si pensa, le modificazioni sinaptiche sono il substrato dell’apprendimento, il feedback ricevuto dall’esterno deve poter influenzare indirettamente, attraverso l’attività neuronale indotta o meccanismi di neuromodulazione (➔), i cambiamenti sinaptici.

Biforcazione tra reti neurali e neuroscienze computazionali

Contemporaneamente allo sviluppo di questi modelli formali, andavano definendosi modelli matematici dettagliati del funzionamento dei neuroni: modelli teorici della generazione e della propagazione dell’impulso nervoso, della propagazione dell’informazione in input al neurone nelle strutture dendritiche. La capacità di tali modelli di dar conto di molte proprietà della dinamica neuronale, che nel frattempo divenivano sperimentalmente accessibili, diede il primo impulso alle neuroscienze computazionali, ossia a un approccio teorico al funzionamento del cervello, in cui le capacità di elaborazione di questo vengono descritte, in un approccio bottom-up, come proprietà emergenti di reti complesse di neuroni e sinapsi (➔ cervello, modelli per l’attività su larga scala del). È importante osservare che, a partire già dagli ultimi anni del secolo scorso, lo sviluppo delle r. n. e quello dei modelli di neuroscienza computazionale si sono sempre più differenziati; i secondi stanno diventando parte integrante dello sforzo teorico necessario a inquadrare l’enorme quantità di dati in neuroscienze in schemi interpretativi e predittivi, i primi, sempre più spogliati delle suggestioni biologiche legate alla terminologia adottata, stanno diventando parte legittima e importante dell’ambito più vasto della statistica multivariata e dell’apprendimento automatico (machine learning).

Imparare da esempi e generalizzare

Formalmente il perceptron realizza una partizione di uno spazio che ha dimensionalità pari al numero di unità di input (che chiameremo N): ogni insieme di valori di input si può pensare come un punto in questo spazio (per esempio, per N=2 sarà un piano), e il vettore di pesi sinaptici che realizza la corretta corrispondenza input-output definisce un iperpiano (N‒1)-dimensionale (una retta per N=2, un piano per N=3, ecc.) a esso perpendicolare che costituisce la frontiera di separazione tra le due classi. I punti (input) che si trovano da una parte del piano corrispondono alla risposta 0 del perceptron, quelli dall’altro lato alla risposta 1. Durante la procedura iterativa di apprendimento, mano a mano che si susseguono gli esempi e che i pesi vengono modificati come abbiamo spiegato sopra, l’iperpiano si muoverà finché si posizionerà in modo da separare in due classi i punti (esempi), che risultano etichettati 1 o 0 secondo la prescrizione desiderata. Ora è chiaro che questo non sarà possibile per una distribuzione arbitraria di punti e di etichette prescritte; i casi in cui esiste effettivamente un iperpiano in grado di separare i punti con etichette diverse si dicono linearmente separabili. Una domanda istruttiva, a cui ha risposto Thomas M. Cover nel 1965, è la seguente: se si scelgono a caso le etichette binarie di M input di esempio nello spazio N-dimensionale, quante delle 2M possibili etichettature (regole) sono linearmente separabili? La risposta è: se M/N<1, tutte; se 1<M/N<2, quasi tutte (la frazione di regole non imparabili tende a 0 se N tende all’infinito, per M/N costante); se M/N>2, quasi nessuna (la frazione di regole imparabili tende a 0 se N tende all’infinito, per M/N costante). Si noti che la frazione di regole imparabili passa da ‘quasi tutte’ a ‘quasi nessuna’ per un certo valore di M/N, e che questo passaggio è tanto più brusco quanto più grande è N; il valore di passaggio tra questi due regimi determina la capacità della rete.

Memorizzazione vs. generalizzazione

Possiamo ora riprendere in modo più circostanziato la domanda sulla capacità di generalizzazione di una r. n.: ammesso che la procedura di apprendimento degli M esempi abbia avuto successo, qual è la probabilità che, dopo aver congelato i pesi sinaptici, l’errore compiuto dalla rete sia piccolo o nullo su un nuovo esempio, non utilizzato nell’addestramento? Il legame tra la capacità della rete e la sua capacità di generalizzazione viene stabilito formalmente dalla cosiddetta dimensione di Vapnik-Chervonenkis, dVC, definita in modo che per M<dVC tutte le 2M etichettature siano imparabili, per almeno una scelta degli M esempi. Ora, immaginiamo che la rete (con N fissato) abbia appreso perfettamente M esempi, e che venga a essa sottoposto un ulteriore esempio; al di sotto della capacità, poiché la maggior parte delle regole è imparabile dalla rete, lo saranno anche, probabilmente, le due regole che includono le due possibili etichette associate all’esempio M+1 di test, a parità di etichette associate agli M esempi appresi, il che implica una indeterminazione della etichetta dell’esempio di test. Se invece ci troviamo al di sopra della capacità, la rete potrà imparare una piccola frazione delle possibili regole; tuttavia se ne ha appreso una a partire dagli M esempi, questa determinerà quasi univocamente l’insieme di pesi corrispondente, e quindi l’etichetta dell’esempio di test, il che equivale a dire che la rete ha una buona proprietà di generalizzazione. La teoria di Vapnik-Chervonenkis è molto generale, e trascende il caso specifico delle r. n. tipo perceptron. Il messaggio fondamentale di questi sviluppi formali è però abbastanza intuitivo: una rete con capacità molto grande può imparare moltissime regole ma, proprio per questo, avere cattive proprietà di generalizzazione (la rete memorizza gli esempi di addestramento); d’altra parte una rete con capacità bassa esprime facilmente una buona generalizzazione. In altre parole, la generalizzazione appare quando si esaurisce la memorizzazione. In effetti si può dimostrare che, in reti generiche (in cui si possono anche avere, come descriveremo in seguito, strati di neuroni ‘nascosti’ tra input e output), l’errore compiuto sugli esempi di addestramento diminuisce all’aumentare della complessità della rete (numero di pesi sinaptici disponibili), mentre la differenza tra questo errore di addestramento e l’errore di generalizzazione (su esempi di test) aumenta; la somma di queste due quantità, in funzione della complessità della rete, ha quindi un minimo, che corrisponde in qualche modo alla rete ottimale. Si consideri che le stime di cui sopra sono spesso definite del caso peggiore, nel senso che, nel formalismo matematico che serve a ricavarle, si assume che gli esempi siano tratti da una arbitraria distribuzione di probabilità; tali stime si rivelano quindi spesso troppo pessimistiche, visto che le distribuzioni di reale interesse applicativo hanno notevoli proprietà di regolarità. Esiste un approccio complementare agli stessi problemi, che usa gli strumenti della meccanica statistica, e che fornisce stime di caso tipico.

Problemi di classificazione più complicati

Nel caso del perceptron, imparare la regola consiste nel trovare i pesi che definiscono l’iperpiano di separazione tra le classi. In realtà molti problemi di classificazione richiedono frontiere di separazione tra le classi molto più complicate. L’estensione a questi casi più complicati è stata affrontata essenzialmente secondo due approcci. Il primo consiste nell’arricchire l’architettura della rete, e nel formulare procedure iterative di apprendimento che siano adatte a tali architetture (perceptron multistrato). Il secondo approccio realizza manipolazioni dell’insieme originario di esempi, in modo che sia possibile proiettare il problema in uno spazio di dimensionalità più elevata, nel quale la classificazione si possa di nuovo ottenere mediante un iperpiano (support vector machines). Perceptron multistrato. Il passo fondamentale nello sviluppo del primo approccio è consistito nel considerare reti in cui l’informazione si propaga, come nel perceptron, dall’input all’output, senza rami di feedback, ma passando attraverso uno o più strati di neuroni nascosti. Notiamo come tutte queste reti feedforward siano prive di dinamica, e costituiscano essenzialmente filtri statici (esistono estensioni a reti con linee di feedback, qui non considerate). La relazione input-output per i neuroni di queste reti è tipicamente di tipo sigmoide: l’output è una funzione crescente dell’input, con una saturazione per input elevati. È intuitivo che tali architetture hanno potenzialità superiori a quelle del perceptron. In effetti (allargando per un momento la prospettiva al di là dei problemi di classificazione) è stato dimostrato negli anni Novanta del 20° sec. che i perceptron multistrato sono ‘approssimatori universali parsimoniosi’. Con ciò si intende che gli output di queste reti possono approssimare con accuratezza arbitraria qualsiasi funzione non lineare (purché abbastanza regolare), e sono parsimoniosi perché, rispetto ad altri approssimatori universali (per es., i polinomi), a parità di accuratezza necessitano di un numero inferiore di parametri (in questo caso i pesi sinaptici). In tale contesto, il problema della generalizzazione si presenta come l’identificazione del migliore fit di una funzione a partire da un numero limitato di punti (gli esempi); così come in statistica la scelta dell’ordine del fit è complicata dal fatto che non si conosce a priori la complessità della funzione, allo stesso modo nel caso delle r. n. la ricchezza dell’architettura può essere, a seconda del problema, sottodimensionata o sovradimensionata (in sostanza, troppi o troppo pochi pesi sinaptici), ed entrambe le situazioni comportano problemi, analogamente a quanto visto sopra. Se l’architettura è troppo povera, i gradi di libertà offerti dai pesi sinaptici non sono sufficienti a minimizzare l’errore compiuto dalla rete sugli esempi di addestramento. Se però l’architettura è troppo ricca (il numero di pesi sinaptici è troppo elevato) si arriva a una soluzione in cui la rete compie un errore molto piccolo sugli esempi di addestramento, ma questo può corrispondere a prestazioni mediocri su esempi inediti della stessa regola (la situazione cosiddetta di overfitting). Il problema è, naturalmente, identificare una procedura di apprendimento idonea per questo tipo di reti. Estendendo l’idea dell’apprendimento supervisionato del perceptron, nel caso tipico dell’algoritmo detto backpropagation l’apprendimento supervisionato nel perceptron multistrato procede misurando l’errore nell’output della rete, esprimendolo come funzione dei pesi della rete, e modificando i pesi in ragione della responsabilità di ognuno nell’errore commesso; in altre parole, il procedimento iterativo realizza una gradient descent (discesa di gradiente) rispetto a una funzione errore, che dipende dai pesi della rete. Questa procedura, proposta negli anni Ottanta del 20° sec., si è evoluta in una serie di varianti. Malgrado l’analogia suggerita tra l’algoritmo del perceptron e la backpropagation, c’è una differenza importante: se la regola non è imparabile dal perceptron, rimane desiderabile trovare una configurazione di pesi che, come la backpropagation, fornisca un errore minimo; l’algoritmo del perceptron non raggiunge questo scopo, e se non si può ottenere un errore nullo, bisogna adottare una diversa procedura per ottenere quello minimo. Un caso interessante di reti feedforward è quello del cosiddetto autoencoder: una rete a tre strati, in cui lo strato di input e quello di output hanno lo stesso numero di neuroni, e quello intermedio (nascosto) un numero di neuroni inferiore. La rete viene addestrata semplicemente a riprodurre in output, per ogni esempio, la stessa configurazione di attività in input. L’aspetto notevole del problema è che, a causa del minor numero di neuroni nello strato nascosto, se la rete riesce a imparare gli esempi, e a generalizzare in misura accettabile, si è realizzata una compressione di informazione: lo stato dei neuroni nascosti fornisce, per ogni esempio, una versione compressa dello stato comune dell’input e dell’output. Nei primi esempi di tali reti, nella metà degli anni Ottanta, si è ottenuta in questo modo una compressione di semplici immagini, non lontana per prestazioni da quella ottenibile con metodi standard e più complicati. L’interesse per gli autoencoders è stato ravvivato di recente (2006) da alcuni autori che hanno elaborato una strategia efficiente per migliorare la procedura di apprendimento in questo tipo di reti (solitamente molto lenta e non sempre efficace), mediante una procedura di preaddestramento che fornisce una buona condizione iniziale dei pesi per la procedura di apprendimento.

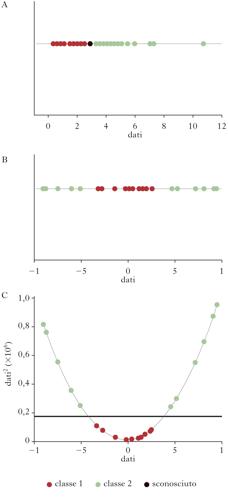
Support vector machines. Le support vector machines (SVM), anche se spesso non vengono incluse nelle r. n. propriamente dette, ne rappresentano una naturale evoluzione rispetto ai problemi di classificazione e di riconoscimento di pattern. Riprendiamo il caso in cui è possibile individuare un iperpiano che separa i dati in due classi. Osserviamo innanzi tutto che, nel caso di un insieme di esempi linearmente separabili, esisteranno in generale più iperpiani che realizzano tale separazione. Ci si può chiedere quale sia il migliore, nel senso di assicurare le migliori proprietà di classificazione su nuovi dati (generalizzazione); è abbastanza naturale identificare l’iperpiano ottimale come quello che massimizza la distanza dai punti più vicini delle due classi (il cosiddetto margine). Inoltre, ci si aspetta in generale che alcuni punti ‘anomali’ di una classe possano situarsi in mezzo a quelli dell’altra classe, e che tali casi vadano in qualche modo ignorati nella definizione dell’iperpiano ottimale di separazione tra le classi; si configura dunque un compromesso tra l’ampiezza del margine e la probabilità di errata classificazione. Tuttavia, molti problemi di classificazione non sono linearmente separabili. Per capire come le tecniche SVM risolvono questo problema, si consideri il caso semplice di una dimensione: in questo caso l’iperpiano di separazione si riduce a un punto. Si può verificare che non si possono separare le due classi con un punto; si può allora aggiungere una dimensione al problema, aggiungendo un nuovo asse, lungo il quale viene riportato il quadrato dei dati originari: in questo nuovo spazio il problema può diventare linearmente separabile. Però è possibile dimostrare che attraverso l’uso di un kernel, ossia una trasformazione (in genere non lineare) dei dati, si può proiettare il problema originario in uno spazio a dimensione più alta, in cui esso sia linearmente separabile, come dimostra l’esempio in figura. Se, come si può dimostrare, questo è in generale possibile, sembrerebbe ovvio adottare sempre la strategia di proiettare il problema in uno spazio di dimensione elevata; sorge però un problema analogo a quello menzionato dell’overfitting: l’iperpiano di separazione che si trova nello spazio a dimensione elevata, una volta proiettato sullo spazio originario, definisce frontiere di decisione molto specifiche per i dati di esempio, e le proprietà di generalizzazione non risultano buone. Si determina quindi l’esigenza di una ricerca euristica del miglior compromesso, analoga a quella necessaria nei perceptron multistrato.