reticolo

reticolo

reticolo in algebra, insieme R dotato di un ordinamento parziale (largo) tale che per ogni coppia di elementi a e b di R, sono definiti il loro → minimo comune maggiorante (denotato con a ∨ b) e il loro → massimo comune minorante (denotato con a ∧ b). Equivalentemente, un reticolo può essere definito in modo puramente algebrico come un insieme R dotato di due operazioni binarie interne ∧ e ∨ associative e commutative rispetto alle quali ogni elemento di R è idempotente (→ idempotenza) e che sono legate dalle seguenti leggi di assorbimento:

Un reticolo è una struttura doppia: esso è contemporaneamente una struttura algebrica e una struttura d’ordine e tali strutture risultano inoltre essere equivalenti, nel senso che, a partire da una qualsiasi di esse, è possibile definire l’altra. Esempio base di reticolo è l’insieme delle parti ℘(A) di un dato insieme A, con le operazioni di unione e intersezione; per questo, alcuni testi utilizzano per le operazioni definite in un qualsiasi reticolo i simboli delle operazioni insiemistiche ∩ e ∪. In aritmetica costituiscono un reticolo i numeri naturali quando si assumano come intersezione e unione di due numeri il loro massimo comune divisore e, rispettivamente, il minimo comune multiplo (o anche viceversa).

Un reticolo R si dice completo se ogni sottoinsieme di R ha estremo superiore ed estremo inferiore (in tali reticoli si possono introdurre le nozioni di limite e di convergenza); ogni insieme totalmente ordinato è un reticolo completo. Un insieme totalmente ordinato si dice inoltre distributivo se vale una delle due seguenti proprietà equivalenti e duali tra loro (→ dualità), per ogni scelta di a, b, c:

R si dice invece modulare se, per ogni scelta di a, b, c, tali che b preceda a, risulta

Ogni reticolo distributivo è in particolare modulare. I reticoli modulari costituiscono una classe di reticoli di notevole interesse: sono, per esempio, modulari il reticolo dei sottogruppi di un gruppo abeliano e il reticolo degli ideali destri (o sinistri) di un anello.

Se esistono, gli elementi neutri delle operazioni ∧ e ∨ sono detti rispettivamente zero e uno (indicati con i simboli 0 e 1): se esistono, essi possono essere equivalentemente definiti rispetto alla struttura d’ordine del reticolo come l’unico elemento che precede ogni altro elemento di R e come l’unico elemento che è preceduto da ogni altro elemento di R. Un reticolo si dice complementato se è dotato di tali elementi neutri e se in aggiunta, per ogni elemento a di R, esiste un elemento ￢a (detto il complemento di a, e indicato anche con ā) tale che a ∨ ￢a = 1 e a ∧ ￢a = 0: il complemento di a coincide quindi con il suo inverso rispetto ad ambedue le operazioni ∧ e ∨. Per esempio, l’insieme delle parti di un insieme S è un reticolo completo, distributivo, complementato in cui lo zero è l’insieme vuoto e in cui l’unità è l’insieme S.

Un reticolo distributivo e complementato è detto algebra di → Boole.

La nozione di prodotto diretto di reticoli consente di ottenere nuovi reticoli a partire da due o più reticoli assegnati. Siano R, S due reticoli; l’insieme delle coppie ordinate (r, s) con r ∈ R, s ∈ S costituisce un nuovo reticolo T (che si chiama prodotto diretto di R, S e si denota con R × S) se in tale insieme si introducono le operazioni di unione e di intersezione al modo seguente:

Subreticoli

Un sottoinsieme proprio S di un insieme finito R dotato di ordinamento parziale (largo) ≤ è ancora un insieme parzialmente ordinato rispetto all’ordinamento definito su R. Possono tuttavia presentarsi tre diverse situazioni:

• S è un subreticolo di R, nel senso che sia a ∨ b sia a ∧ b forniscono in S lo stesso risultato che in R;

• S è un reticolo, ma non è un subreticolo di R perché a ∨ b oppure a ∧ b forniscono risultati diversi da quelli che si hanno in R;

• S non è un reticolo.

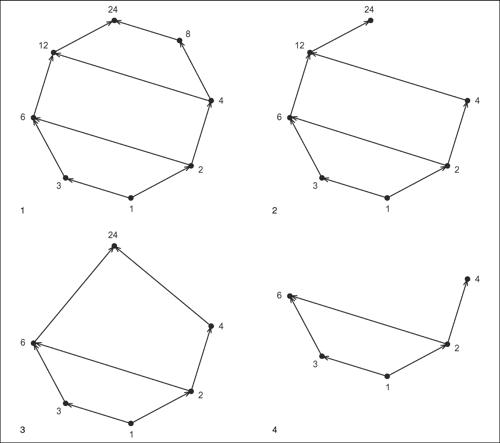
Per esempio, nell’insieme R = {1, 2, 3, 4, 6, 8, 12, 24} dei divisori di 24, con l’ordinamento a ≤ b se a | b (a divide b), che è un reticolo, il suo sottoinsieme S₁ = {1, 2, 3, 4, 6, 12, 24} è un subreticolo di R. Il sottoinsieme S₂ = {1, 2, 3, 4, 6, 24} è un reticolo, ma non è un subreticolo di R perché in R si ha 4 ∨ 6 = 12 mentre in S₂ si ha 4 ∨ 6 = 24. Infine, S₃ = {1, 2, 3, 4, 6} non è un reticolo perché 4 e 6 non hanno minimo comune maggiorante in S₃.

Diagramma di un ordinamento

È possibile rappresentare la struttura dell’ordinamento ≤ di un reticolo attraverso un grafo, detto diagramma dell’ordinamento, i cui nodi sono gli elementi dell’insieme e due elementi a, b sono collegati da un arco orientato (una freccia dal nodo a al nodo b) se a ≤ b e non esiste in R alcun elemento intermedio ai due (tale cioè che a ≤ x ≤ b). Tale diagramma permette di “vedere” se, in tale insieme, ogni coppia di elementi ha un minimo comune maggiorante (l’elemento verso cui convergono i cammini orientati che hanno origine in a e b) e un massimo comune minorante (l’elemento da cui hanno origine i cammini orientati che terminano in a e b). È anche attraverso il diagramma che si può analizzare se un sottoinsieme di un reticolo R è ancora un reticolo e se è un subreticolo di R.