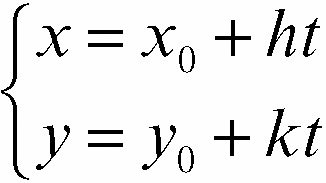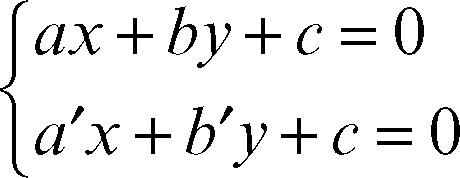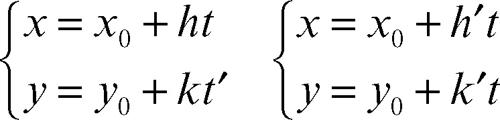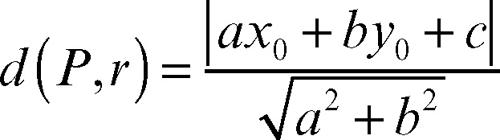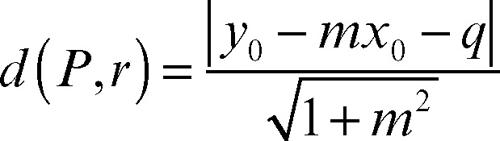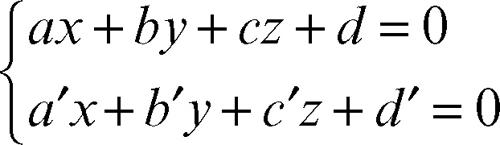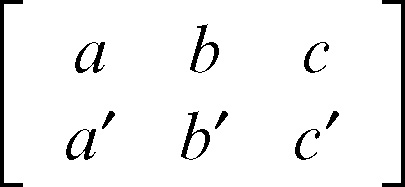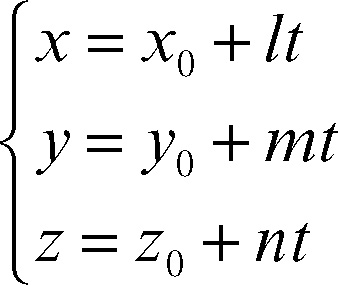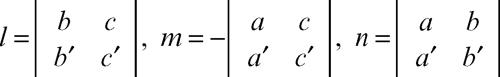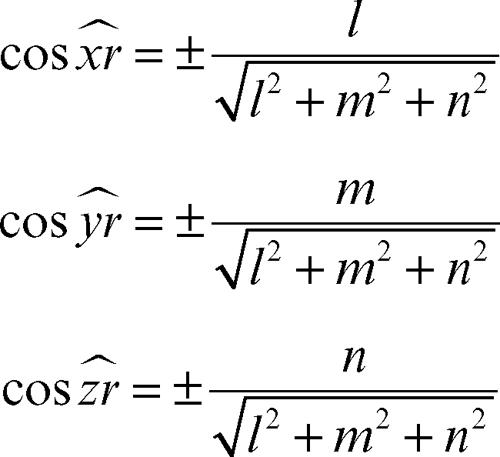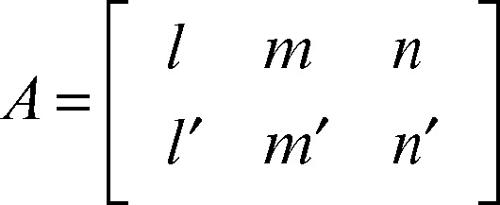retta

retta

retta ente fondamentale della geometria, insieme al punto e al piano, considerato nella geometria euclidea un concetto primitivo, non suscettibile di definizione autonoma. Il suo significato è precisato attraverso il sistema di assiomi scelto per caratterizzare la geometria stessa (→ geometria euclidea; → definizione). In termini intuitivi, la retta è descrivibile come una linea senza curvature e spigolosità illimitata nelle due direzioni; può essere descritta anche come un insieme continuo ordinato di punti che si susseguono in modo che tra due qualsiasi di essi ci sia sempre il minimo percorso e che abbia dimensione 1. Per la retta valgono, quindi, le seguenti proprietà: 1) la retta ha dimensione 1; 2) per un punto del piano o dello spazio passano infinite rette; 3) per due punti distinti A e B (nel piano come nello spazio) passa una e una sola retta; 4) il tratto di retta (segmento) compreso tra A e B rappresenta il cammino più breve che collega A e B; 5) una retta è divisa da ogni suo punto in due parti (semirette) aventi in comune quel solo punto: il punto è detto origine delle due semirette e ciascuna semiretta è illimitata in una sola direzione; 6) sulla retta si possono fissare due ordinamenti totali dei suoi punti, detti versi; fissato un ordinamento, la retta si dice orientata e dati su essa due punti distinti A e B, si ha che «A segue B» oppure «B segue A» (→ orientamento; → Hilbert, assiomi di).

Nello spazio tridimensionale una retta è univocamente individuata da due punti, da un punto e da una direzione, oppure da due piani non paralleli. Rispetto a un piano essa può essere parallela (non ha alcun punto in comune con il piano oppure vi giace), incidente (ha con esso un punto in comune), giacente sul piano (appartiene al piano); due rette possono appartenere allo stesso piano (e allora si dicono complanari) oppure no e allora si dicono sghembe. Due rette complanari possono risultare:

• parallele, se sono prive di punti comuni oppure sono coincidenti;

• incidenti, se hanno un solo punto in comune.

In particolare, due rette incidenti risultano perpendicolari se formano quattro angoli di uguale ampiezza (che allora risultano retti).

Nel piano euclideo, per ogni retta r e per ogni punto P del piano esiste una sola retta s passante per P e parallela a r (→ parallela, assioma della); analogamente esiste ed è unica la retta s′ perpendicolare per P alla retta r (→ unicità della perpendicolare, teorema della).

Nel piano proiettivo, si dice che due rette parallele hanno lo stesso punto all’infinito (o punto improprio, sinonimo della loro comune direzione); l’insieme di tutti i punti impropri delle rette del piano costituisce la → retta impropria o retta all’infinito, che è la giacitura comune a tutti i piani paralleli di un fascio improprio.

Descrizione analitica di una retta nel piano

Nel piano, dotato di un sistema di coordinate cartesiane Oxy, una retta è rappresentata con una equazione implicita a coefficienti reali, del tipo ax + by + c = 0 (con a e b non entrambi nulli), oppure, se non è parallela all’asse delle ordinate, con una equazione esplicita a coefficienti reali, del tipo y = mx + q. L’equazione di una retta per l’origine si ottiene, in ciascuna delle due forme precedenti, uguagliando a zero il termine noto.

La forma esplicita, che è meno generale perché non può essere utilizzata per rappresentare rette parallele all’asse delle ordinate, fornisce indicazioni sulla posizione della retta nel piano, in particolare:

• il parametro m, detto coefficiente angolare, fornisce l’inclinazione o pendenza della retta, rispetto all’asse delle ascisse e ne individua la → direzione;

• il parametro q indica l’ordinata del punto in cui la retta interseca l’asse delle ordinate.

Una retta che interseca gli assi coordinati nei punti di coordinate (p, 0) e (0, q) è rappresentata da un’equazione del tipo

detta equazione segmentaria della retta. Le equazioni

dette equazioni parametriche della retta in un piano, rappresentano la retta passante per il punto P(x₀, y₀) e parallela al vettore v di componenti (h, k), detto vettore direzione. Tali equazioni possono essere scritte anche come equazione vettoriale

I coefficienti h e k, definiti a meno di un fattore non nullo di proporzionalità, sono detti parametri direttori della retta, mentre si dicono coseni direttori i coseni degli angoli convessi che una retta orientata forma con le direzioni positive degli assi coordinati. I coseni direttori di una retta di parametri direttori h e k sono:

In coordinate polari, una retta per l’origine ha un’equazione del tipo θ = k, mentre una retta non passante per l’origine ha equazione del tipo aρcosθ + bρsinθ + c = 0.

L’equazione di una retta passante per due punti P₁(x₁, y₁), P₂(x₂, y₂), con x₁ ≠ x₂, è

Se invece x₁ = x₂ = k ∈ R, la retta ha equazione x = k ed è parallela all’asse delle ordinate.

Per determinare analiticamente l’intersezione di due rette si risolve il sistema lineare

formato dalle equazioni delle due rette. A seconda che il sistema risulti determinato, indeterminato o impossibile, le rette rappresentate risultano, rispettivamente, incidenti, parallele coincidenti, parallele distinte; cioè hanno, rispettivamente, uno, tutti o nessun punto in comune. In generale l’intersezione di due o più rette si determina risolvendo il sistema lineare formato dalle equazioni delle rette.

La condizione di parallelismo e la condizione di perpendicolarità tra due rette dipendono dal tipo di equazioni e di coordinate con cui le rette sono rappresentate. Date pertanto due rette

• di equazioni cartesiane esplicite

• di equazioni cartesiane implicite

• di equazioni parametriche

esse sono parallele se e solo se si verificano, rispettivamente, le seguenti condizioni di parallelismo:

• ab′ − a′b = 0

• m = m′

• hk′ −h′k = 0

Le rette sono perpendicolari se e solo se si verificano, rispettivamente, le seguenti condizioni di perpendicolarità:

• aa′ + bb′ = 0

• mm′ = −1

• hh′ + kk′ = 0

In forma implicita, l’insieme delle rette passanti per un punto P₀(x₀, y₀) (esclusa quella parallela all’asse delle ordinate) è descritto, al variare di m e q, dall’equazione y − y₀ = m(x − x₀). Utilizzando la condizioni di parallelismo (rispettivamente, di perpendicolarità) si può pertanto scrivere l’equazione di una retta passante per un punto P₀ dato e parallela (rispettivamente, perpendicolare) a una retta data.

La distanza di un punto P(x₀, y₀) da una retta r di equazione ax + by + c = 0 è

Se la retta è assegnata mediante l’equazione y = mx + q la distanza è

Descrizione analitica di una retta nello spazio

Nello spazio tridimensionale, dotato di un sistema di riferimento cartesiano Oxyz, una retta è rappresentata in forma cartesiana da un sistema lineare del tipo

in cui la matrice

ha rango 2. In termini geometrici ciò vuol dire che una retta è assegnata come intersezione di due piani non paralleli.

Le equazioni di una retta possono essere date anche in forma parametrica. Assegnato un suo punto P(x₀, y₀, z₀) e un vettore direzione v di componenti (l, m, n), le equazioni parametriche della retta sono:

Tali equazioni possono essere scritte anche come equazione vettoriale

Il passaggio da una rappresentazione all’altra avviene utilizzando le seguenti relazioni:

Normalizzando i parametri direttori l, m, n di una retta si ottengono i suoi coseni direttori:

Due rette, di rispettivi parametri direttori (l, m, n) e (l′, m′, n′), sono parallele se solo se i rispettivi vettori direzione sono paralleli; pertanto, la condizione di parallelismo di due rette nello spazio è che risulti uguale a 1 il rango della matrice

Due rette incidenti risultano perpendicolari se e solo se i rispettivi vettori direzione sono ortogonali; pertanto, la condizione di perpendicolarità di due rette nello spazio è che risulti nullo il prodotto scalare dei vettori direzione, cioè ll′ + mm′ + nn′ = 0.

Nello spazio, la distanza di un punto P da una retta t si ottiene calcolando la distanza di P dal punto in cui il piano per P ortogonale a t interseca t. La distanza tra due rette sghembe è data dalla distanza tra due piani paralleli passanti, rispettivamente, per ciascuna delle due rette. Tali piani sono univocamente determinati perché, date due qualsiasi rette sghembe, per ognuna di esse passa uno e un solo piano parallelo all’altra.