sfera
Enciclopedia on line
sfera In geometria, figura solida formata dai punti dello spazio aventi da un punto fissato (centro della s.) distanza minore o uguale di un segmento dato (raggio della s.).
Matematica
Definizioni e proprietà [...] gradi) formato da due semipiani, l’area del fuso è data da πR2α/90. Poligono sferico Una parte di superficie sferica delimitata da archi di cerchi massimi. Segmento sferico a una base La parte di s. delimitata da un piano secante. Il volume è dato da ...
Leggi Tutto
MATEMATICA
Enciclopedia Italiana (1934)
MATEMATICA
Federico Enriques
Matematica, o matematiche (gr. τὰ μαϑηματικά da μάϑημα "insegnamento") significa originariamente "disciplina" o "scienza razionale". Questo significato conferirono alla [...] (sec. II d. C.) e poi di Claudio Tolomeo: dai quali esce - in particolare - una trigonometria; cioè il calcolo delle corde degli archi circolari, e il lemma di Tolomeo che dà per esse il teorema d'addizione. Nuovi problemi spuntano nella teoria degl ...
Leggi Tutto
Vicino Oriente antico. La matematica
Storia della Scienza (2001)
Vicino Oriente antico. La matematica
Jöran Friberg
La matematica
Gli esercizi metro-matematici nel III millennio
La ricerca sulla matematica mesopotamica conobbe il suo periodo pionieristico a partire [...] esercizi, dove alcuni quadrati di lato 60 pertiche sono divisi in vari modi in parti più piccole delimitate da linee rette e archi di circonferenza, e dove l'obiettivo è quello di identificare le parti con il loro nome e trovarne l'area (v. oltre ...
Leggi Tutto
CATEGORIA:
STORIA DELLA MATEMATICA
L'Ottocento: matematica. La geometria non euclidea
Storia della Scienza (2003)
L'Ottocento: matematica. La geometria non euclidea
Rossana Tazzioli
La geometria non euclidea
Alla base dei suoi Elementi Euclide aveva posto un certo numero di definizioni (o 'termini') e di assiomi [...] loro distanze è s′=sex, dove a e b sono due oricicli, x la loro distanza e s, s′ le lunghezze di due diversi archi.
Nella geometria euclidea e=1, e dunque s=s′ (due rette parallele sono equidistanti). Nella geometria immaginaria si ha invece e>1 ...
Leggi Tutto
La civiltà islamica: antiche e nuove tradizioni in matematica. La rinascita degli studi geometrici nel mondo latino
Storia della Scienza (2002)
La civilta islamica: antiche e nuove tradizioni in matematica. La rinascita degli studi geometrici nel mondo latino
Menso Folkerts
La rinascita degli studi geometrici nel mondo latino
La tradizione [...] necessario operare con segmenti correlati agli angoli o agli archi. I matematici greci scelsero a questo fine la corda de proportione et proportionalitate. Nel primo vengono dedotti teoremi su archi di cerchio e corde che vanno oltre il contenuto del ...
Leggi Tutto
DE SCHWARZ, Maria Giuseppina
Dizionario Biografico degli Italiani (1991)
DE SCHWARZ, Maria Giuseppina
Gianni Battimelli
Nacque a Trieste il 2 ag. 1909 da Lotario, ufficiale della marina austroungarica, e da Lucia Kapsa. La madre era di origine polacca, il padre austrotedesco. [...] in Österreichisches Ingenieur-Archiv, VII (1957), pp. 88-100; altri lavori connessi coi precedenti riguardano l'instabilità di archi e gli spostamenti di una piastra elettrica isotropa in condizioni opportune di propagazione (come, ad es., Su alcune ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
La scienza in Cina: i Ming. Matematica e astronomia
Storia della Scienza (2001)
La scienza in Cina: i Ming. Matematica e astronomia
Guo Shirong
Li Zhaohua
Alexei Volkov
Peter Engelfriet
Chu Pingyi
Matematica e astronomia
La perdita delle conoscenze matematiche e astronomiche
di [...] , 1275) e di Gu Yingxiang (Procedimenti matematici per il triangolo rettangolo e Procedimenti per il calcolo di ' segmenti e archi', v. par. 1). Vi sono inoltre somiglianze con varie opere di epoca Ming, quali le già citate Spiegazioni dettagliate ...
Leggi Tutto
L'Età dei Lumi: matematica. Geometria analitica, delle curve e delle superfici. Il problema delle parallele
Storia della Scienza (2002)
L'Eta dei Lumi: matematica. Geometria analitica, delle curve e delle superfici. Il problema delle parallele
Peter Schreiber
Geometria analitica, delle curve e delle superfici. Il problema delle parallele
A [...] permettevano di risolvere, spesso in modo elegante, problemi riguardanti la direzione di tangenti, la curvatura, la lunghezza di archi, il volume della superficie generata, ecc., per intere classi di curve e anche per molte curve particolari da poco ...
Leggi Tutto
L'Ottocento: matematica. Metodi del calcolo numerico
Storia della Scienza (2003)
L'Ottocento: matematica. Metodi del calcolo numerico
Dominique Tournès
Metodi del calcolo numerico
Prima del 1870 l'analisi numerica non si era ancora sviluppata come disciplina autonoma; esisteva [...] curva integrale con una successione di piccoli segmenti di tangenti, si pensa anche a utilizzare una successione di piccoli archi di cerchi osculatori. Il procedimento è particolarmente adatto a un'equazione del secondo ordine:
perché è noto che il ...
Leggi Tutto
Tolomèo, Claudio
Enciclopedia on line
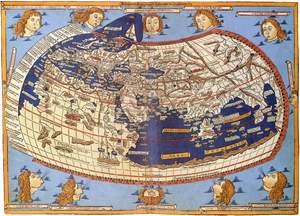 Astronomo, matematico e geografo (n. 100 d. C. circa - m. dopo il 170), vissuto ad Alessandria. Della sua vita conosciamo soltanto quello che si può ricavare dalle sue opere. La sua opera principale è [...] modello deferente-epiciclo non è sufficiente per descrivere i moti retrogradi dei pianeti, perché può generare soltanto archi di retrogradazione (costanti contrariamente a ciò che si osserva), T. costruì modelli combinati a deferente eccentrico (v ...
Leggi Tutto
Astronomo, matematico e geografo (n. 100 d. C. circa - m. dopo il 170), vissuto ad Alessandria. Della sua vita conosciamo soltanto quello che si può ricavare dalle sue opere. La sua opera principale è [...] modello deferente-epiciclo non è sufficiente per descrivere i moti retrogradi dei pianeti, perché può generare soltanto archi di retrogradazione (costanti contrariamente a ciò che si osserva), T. costruì modelli combinati a deferente eccentrico (v ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE