FISICA
Enciclopedia Italiana - III Appendice (1961)
FISICA (XV, p. 473; App. II, 1, p. 950)
Giuseppe TEDONE
In questo articolo si dà uno sguardo d'insieme a orientamenti e problemi attuali della fisica. Per una più particolare informazione sui varî rami [...] " mediante una "funzione d'onda", ψ, in generale complessa, priva di qualsiasi significato fisico immediato, ma soddisfacente all'equazione differenziale che regge la propagazione ondosa: l'integrale del quadrato del modulo di ψ esteso a una certa ...
Leggi Tutto
KRAMERS, Hendrich Anthony
Enciclopedia Italiana - II Appendice (1949)
KRAMERS, Hendrich Anthony
Piero CALDIROLA
Fisico teorico, nato a Rotterdam il 17 dicembre 1894; iniziò la sua attività a Leida sotto la guida di H. A. Lorentz e di B. Ehrenfest e la proseguì, dal 1916 [...] della luce e il perfezionamento di un metodo (detto di Wentzel-Kramers-Brillouin) per l'integrazione approssimata dell'equazione di Schrödinger. È autore di un'estesa monografia in due volumi che fa parte dell'Hand- undJahrbuch der chemischen ...
Leggi Tutto
rappresentazione
Dizionario delle Scienze Fisiche (2012)
rappresentazione
rappresentazióne [Der. del lat. repraesentatio -onis, dal part. pass. repraesentatus del lat. repraesentare "rappresentare", comp. di re- "di nuovo" e praesentare "presentare"] [ALG] [...] : v. invarianti, teoria degli: III 285 f. ◆ [ANM] R. analitica: di una curva, di una superficie, ecc., è un'equazione o un insieme di equazioni che esprimono i legami tra le coordinate di un punto della curva o della superficie. ◆ [ANM] R. ciclica: v ...
Leggi Tutto
polare 2
Dizionario delle Scienze Fisiche (1996)
polare 2
polare2 [s.f. dall'agg. polare] [MCF] P. dell'urto: rappresenta, nel piano odografico, la velocità di un'onda d'urto: v. aerodinamica supersonica: I 73 f. ◆ [ALG] P. di un punto rispetto a una [...] curva polare: se la curva è di ordine n ed è funzione delle coordinate omogenee xi, f(xi), è la curva, di ordine n-1, di equazione Σixi(ðf/ðxi)=0. Una medesima curva C ha perciò ∞2 p. (una per ogni punto P nel piano) che costituiscono una rete. Le p ...
Leggi Tutto
parametro
Dizionario delle Scienze Fisiche (1996)
parametro
paràmetro [Der. del fr. paramètre "quasi misura", comp. di para- "para-2" e -mètre "-metro"] [ALG] [ANM] Termine usato talora come equivalente a variabile indipendente (per es., p. reale, complesso), [...] focale come asse polare, ρ=p(1+ecosϑ), con e eccentricità (→ conica). ◆ [ALG] P. di una retta: se ax+by+c=0 è l'equazione cartesiana di una retta nel piano, è la quantità c, al variare continuo della quale (fermi restando a,b) si hanno tutte le rette ...
Leggi Tutto
cilindro
Dizionario delle Scienze Fisiche (1996)
cilindro
cilindro [Der. del lat. cylindrus, dal gr. ky´lindros, che è da kylíndo "rotolare"] [ALG] Superficie geometrica elementare che s'ottiene facendo rotare di un giro completo tre lati di un rettangolo [...] direttrice (v. sopra) è, rispettiv., un'ellisse, un'iperbole, una parabola o, generic., una conica. ◆ [ALG] C. finito, indefinito: v. sopra: [ALG]. ◆ [ALG] Equazione del c.: in coordinate cartesiane, è del tipo f(x-az, y-bz)=0, essendo x-az=y-bz=0 le ...
Leggi Tutto
CATEGORIA:
FISICA MATEMATICA
–
MECCANICA
–
MECCANICA DEI FLUIDI
–
MECCANICA QUANTISTICA
–
TEMI GENERALI
–
ALGEBRA
Einstein, Albert
Enciclopedia on line
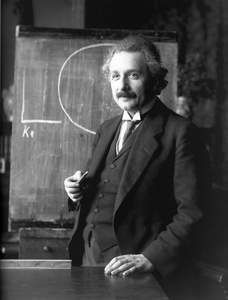Fisico (Ulma 1879 - Princeton 1955). Trascorsi i primi anni della sua vita a Monaco, dopo un breve soggiorno a Milano Einstein si trasferì con la famiglia in Svizzera. A Zurigo completò gli studî secondarî [...] Statistica di E.-Bose: v. statistica. ▭ Per la formula o relazione di E. dell'effetto fotoelettrico, v. fotoelettronico; per l'equazione di E., relativa alla equivalenza fra massa e energia, v. relatività. ▭ Per la legge di Stark-E., v. fotochimica. ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
filo
Enciclopedia on line
Nella tecnica delle costruzioni, sinonimo di spigolo. Unito al nome di una particolare struttura o modanatura (per es., f. muro, f. cornice), indica anche il piano, in genere orizzontale o verticale, [...] la tangente), nel generico punto del f. in condizioni di equilibrio dev’essere soddisfatta l’equazione
ricordata come equazione vettoriale indefinita o equazione fondamentale della statica dei fili. Ai due estremi, per l’equilibrio, devono essere ...
Leggi Tutto
L'Ottocento: matematica. Meccanica analitica
Storia della Scienza (2003)
L'Ottocento: matematica. Meccanica analitica
Helmut Pulte
Meccanica analitica
La meccanica analitica è una branca della meccanica razionale la quale, dopo i primi passi compiuti nel XVII sec., ebbe [...] e finali, (ai,bi,ci) e (xi,yi,zi) oltre al tempo t) e imporre a essa di soddisfare in modo identico le equazioni differenziali alle derivate parziali [21*]. È sufficiente invece considerare S come funzione di 3n+1 quantità (xi,yi,zi e t) e richiedere ...
Leggi Tutto
L'Età dei Lumi: matematica. Le tradizioni principali della meccanica
Storia della Scienza (2002)
L'Eta dei Lumi: matematica. Le tradizioni principali della meccanica
Ivor Grattan-Guinness
Le tradizioni principali della meccanica
Branche della meccanica
La meccanica, nel suo ampio spettro di usi, [...] ) diede inizio alla nuova teoria che porta ancora il suo nome. Anche la moderna nomenclatura riguardante le funzioni e le equazioni a cui ci si è riferiti in questo paragrafo sarebbe stata introdotta nel XIX secolo.
L'epoca di Lagrange
La meccanica ...
Leggi Tutto