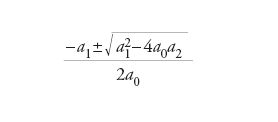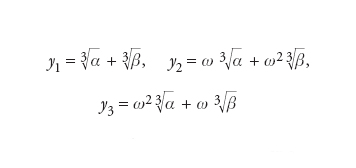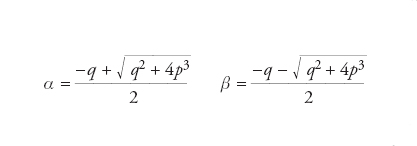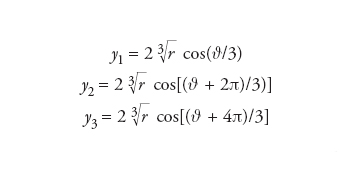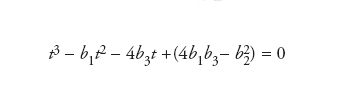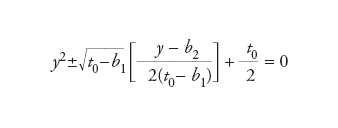risolubilità per radicali

risolubilità per radicali

Procedimento che permette di determinare le radici dell’equazione algebrica a₀xⁿ+a₁xⁿ⁻¹+...+a_n=0 (a₀≠0), a coefficienti reali o complessi, mediante un numero finito di operazioni razionali ed estrazioni di radici, operate sui coefficienti a_i dell’equazione. Tale procedimento caratterizza le equazioni algebriche di grado minore o uguale a 4. Infatti, un’equazione lineare a₀x+a₁=0 ha una sola radice −a₁/a₀. Le radici di un’equazione di secondo grado a₀x²+a₁x+a₂=0 sono

La soluzione per radicali dell’equazione di terzo grado a₀x³+a₁x²+a₂x+a₃=0 si basa sulla risoluzione di una risolvente di secondo grado. Anzitutto, la sostituzione y=x+a₁/3a₀ permette di trasformare l’equazione data nell’equazione y³+3py+q=0, le cui radici sono espresse da

che rappresenta la cosiddetta formula di Tartaglia-Cardano dove

sono le radici della risolvente t²+qt−p³=0 e ω=e^2πi/3 è una radice cubica dell’unità. Le radici possono essere tutte e tre reali oppure una reale e due complesse coniugate. Di particolare interesse è il caso irriducibile, che si presenta quando i coefficienti a_i sono tutti reali e q²+4p³〈0. Posto α=re^iϑ (β=α_) le radici

sono tutte reali. Si deve a Paolo Ruffini la prima dimostrazione rigorosa che in questo caso le radici non si possono determinare solo mediante operazioni razionali ed estrazioni di radici reali. L’equazione di quarto grado a₀x⁴+a₁x³+a₂x²+a₃x+a₄=0 può essere risolta per radicali mediante una risolvente di terzo grado come ha dimostrato Ludovico Ferrari, allievo di Cardano. Con la sostituzione y=x+a₁/4a₀ l’equazione data si trasforma nell’equazione y⁴+b₁y²+b₂y+b₃=0, la cui risolvente di terzo grado è

Le radici dell’equazione di quarto grado sono allora date dalle soluzioni delle due equazioni di secondo grado

dove t₀ è una radice della risolvente. Infine, il teorema di Ruffini-Abel stabilisce che le equazioni algebriche di grado superiore al quarto non sono in generale risolubili per radicali.

→ Matematica: problemi aperti