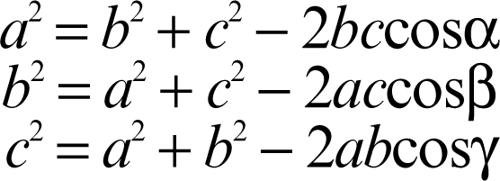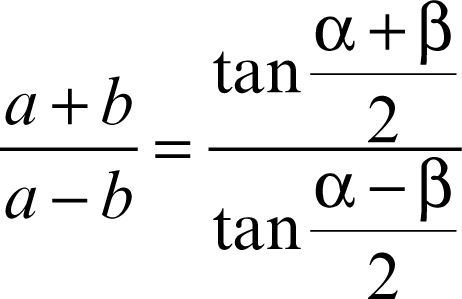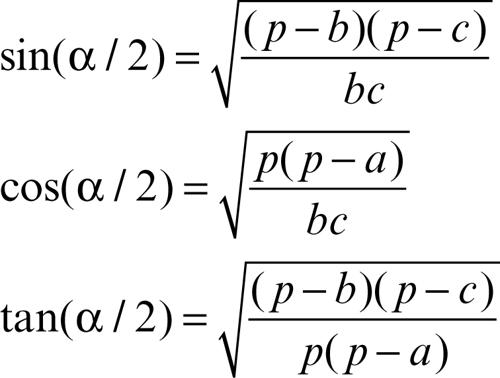triangolo, risoluzione di un

triangolo, risoluzione di un

triangolo, risoluzione di un determinazione di tutti e sei gli elementi fondamentali (lati e angoli) di un triangolo, a partire dalla conoscenza di alcuni di essi: un triangolo di cui sia possibile trovare tutti gli elementi è detto risolubile. Per risolvere un triangolo, se esso è rettangolo, può essere sufficiente applicare il teorema di Pitagora o i teoremi di Euclide. In generale, la risoluzione di un triangolo è possibile solo utilizzando i teoremi della trigonometria.

Risoluzione di un triangolo rettangolo

In un triangolo, esistono alcune relazioni fra i tre lati a, b, c e i tre angoli α, β, γ, ordinatamente opposti ai lati. Tali relazioni sono particolarmente semplici nel caso di un triangolo rettangolo. Un triangolo rettangolo è sempre risolubile se sono noti due elementi (diversi dall’angolo retto) di cui almeno uno deve essere la misura di un lato. Dato il triangolo rettangolo di ipotenusa a e cateti b e c, indicate con β e γ le ampiezze degli angoli opposti rispettivamente a b e c, si hanno i seguenti casi: se sono noti due lati, il terzo lato si ricava utilizzando il teorema di Pitagora (a² = b² + c²); gli altri elementi si ricavano comunque utilizzando le seguenti relazioni: b = asinβ = acosγ; c = asinγ = acosβ; b = ctanβ; c = btanγ. In termini non formali, un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto al cateto o per il coseno dell’angolo adiacente, oppure un cateto è uguale al prodotto dell’altro cateto per la tangente dell’angolo opposto al primo.

Risoluzione di un triangolo qualsiasi

Un triangolo qualsiasi è sempre risolubile noti tre suoi elementi, di cui almeno uno sia un lato. Dato il triangolo ABC, indicate con a, b, c le misure dei lati opposti rispettivamente ai vertici A, B, C, con α, β, γ, rispettivamente, le ampiezze degli angoli in tali vertici e tenendo conto che α + β + γ = π, si utilizzano i seguenti teoremi:

• teorema dei seni:

• teoremi del coseno o di Carnot:

• teorema di Nepero

e analoghe relativamente alle altre coppie di lati del triangolo (→ Nepero, teorema di).

• formule di Briggs per individuare la metà degli angoli del triangolo

con p = (a + b + c)/2 e analoghe per gli altri angoli (→ Briggs, formule di).

Il teorema dei seni e il teorema del coseno sono in generale sufficienti a individuare tutti gli elementi del triangolo. In particolare, il teorema dei seni permette di risolvere un triangolo quando si conoscono un lato e due angoli, oppure due lati e un angolo non compreso tra essi. Il teorema del coseno si utilizza invece quando sono noti tre lati (in tal caso si possono usare anche le formule di Briggs, in particolare quella della tangente, che fornisce in genere un risultato più preciso) oppure due lati e l’angolo tra essi compreso (in questo caso si può usare anche il teorema di Nepero, che consente l’uso dei logaritmi).

Naturalmente, i dati devono essere compatibili con la possibilità di costruire un triangolo, per cui, se sono assegnati tre lati, ogni lato deve essere minore della somma degli altri due e maggiore della loro differenza. Si presenta inoltre un caso in cui, dati due lati e l’angolo non compreso, il problema può risultare insolubile oppure avere due soluzioni. Infatti, se a e b sono le misure dei lati assegnati e β l’ampiezza dell’angolo assegnato, se a > b è possibile che l’altro lato dell’angolo β (di cui dovrebbe far parte c, terzo lato del triangolo) sia esterno alla circonferenza di centro C e raggio b (e allora il problema non è risolubile perché il triangolo “non si chiude”; ciò avviene quando sinβ > b /a), sia tangente a tale circonferenza (e allora il problema ha una sola soluzione: ciò avviene quando sinβ = b /a) oppure infine ne sia secante (e allora il problema ammette come soluzioni due triangoli il cui terzo vertice è uno dei due punti in cui retta e circonferenza si intersecano; ciò avviene quando sinβ < b /a).

Dei vari casi che possono presentarsi si può costruire il seguente schema riepilogativo: