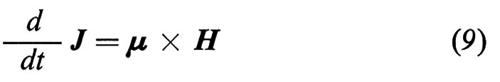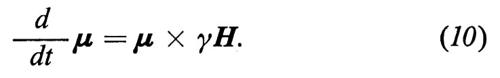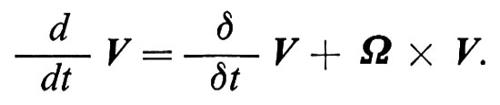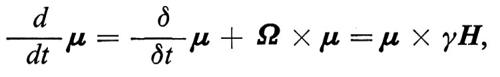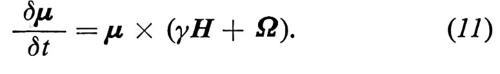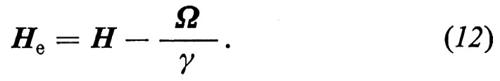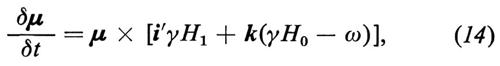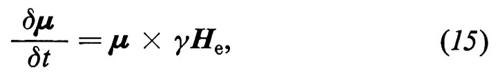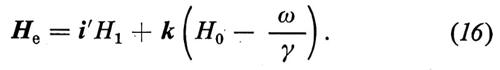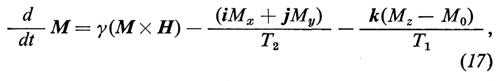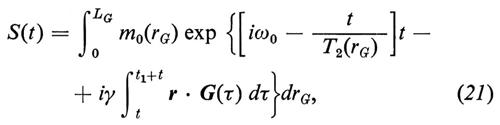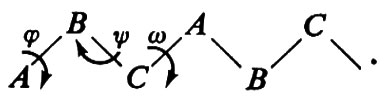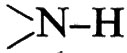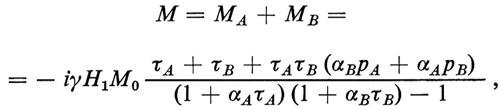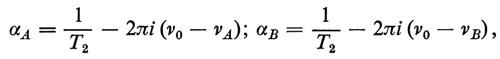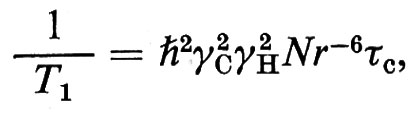Risonanza magnetica nucleare

Risonanza magnetica nucleare

Principi fisici di Bruno Maraviglia

SOMMARIO: 1. Introduzione.  2. Aspetti quantistici elementari.  3. La trattazione classica: a) moto di uno spin isolato; b) l'equazione di Bloch; c) la sequenza spin-eco.  4. Le basi fisiche della tomografia RMN: a) aspetti generali; b) fondamenti teorici; c) apparato sperimentale; d) sviluppi recenti. □ Bibliografia.

1. Introduzione

In generale in fisica si chiamano ‛spettroscopie' quelle tecniche mediante le quali si invia una sonda (onde elettromagnetiche, neutroni, elettroni, ecc.) con proprietà fisiche note in un sistema da indagare e si rivela poi la risposta del sistema alla perturbazione, ricavando in questo modo informazioni sulle sue proprietà fisiche. La risonanza magnetica nucleare (RMN o NMR, Nuclear Magnetic Resonance) è certamente la tecnica spettroscopica più rilevante nell'ambito delle risonanze magnetiche, che comprendono, oltre a quella nucleare, la risonanza paramagnetica elettronica (EPR, Electron Paramagnetic Resonance, o anche ESR, Electron Spin Resonance), la risonanza di quadrupolo nucleare, la risonanza di spin muonico e ogni possibile altra tecnica spettroscopica che permetta di studiare le proprietà magnetiche di un sistema di particelle (particelle elementari, atomi, molecole) usando come sonda onde elettromagnetiche con frequenze corrispondenti alla separazione fra i livelli di energia del sistema magnetico.

Storicamente il primo esperimento di RMN è stato quello dell'americano Rabi (v., 1937), effettuato su fasci atomici per la misura dei momenti magnetici di vari nuclei atomici. Il primo tentativo di RMN in uno stato condensato fu fatto dagli olandesi Gorter e Broer (v., 1942) senza successo, probabilmente a causa della scelta di un campione che successivamente risultò avere un tempo di rilassamento T₁ molto lungo. I primi esperimenti su materia condensata furono realizzati, con successo e indipendentemente, da Purcell, Torrey e Pound (v., 1946) alla Harvard University e da Bloch, Hansen e Packard (v., 1946) alla Stanford University. Per questi esperimenti, che hanno dato l'avvio allo sviluppo tuttora in atto delle risonanze magnetiche, e in particolar modo di quella nucleare, Purcell e Bloch furono assieme insigniti del premio Nobel per la fisica nel 1952.

2. Aspetti quantistici elementari

Tutti i sistemi costituiti da elettroni o da nuclei di atomi che possiedono un momento angolare di spin possono essere studiati con la risonanza magnetica. In particolare un nucleo, formato normalmente da molte particelle, nello stato fondamentale può avere un momento magnetico totale μ e un momento angolare totale J. In generale in RMN lo stato del nucleo è quello fondamentale, in quanto l'energia associata al campo elettromagnetico utilizzato è enormemente inferiore a quella richiesta per una transizione fra stati del nucleo e quindi non si ha mai la possibilità che il nucleo transisca dallo stato fondamentale a uno stato eccitato.

I due vettori μ e J sono paralleli e quindi si può scrivere:

μ = γJ, (1)

dove γ è uno scalare normalmente denominato ‛rapporto giromagnetico'. Da un punto di vista quantistico i vettori μ e J sono naturalmente degli operatori. Abitualmente si definisce un operatore momento angolare adimensionale I secondo la relazione

J = ℏI, (2)

in cui ℏ = h/2π e h è la costante di Planck.

Dalla teoria elementare del momento angolare in meccanica quantistica risulta che I² ha autovalori I (I + 1), dove I è un numero intero (0, 1, 2, ...) o semintero (1/2, 3/2, ...). Ogni componente di I (cioè I_x, I_y e I_z) commuta con I², di conseguenza si possono specificare allo stesso tempo gli autovalori I(I + 1) di I² e m di I_z, con m che può assumere i valori I, I − 1, ..., − I.

L'energia di interazione fra un campo magnetico H e un momento magnetico nucleare μ è data dall'hamiltoniana

ℋ = − μ • H. (3)

Prendendo un sistema di riferimento cartesiano x, y, z, i cui versori indicheremo rispettivamente con i, j e k, con l'asse z coincidente con la direzione del campo magnetico, che assumiamo statico e omogeneo, abbiamo H = H₀ = H₀k. L'hamiltoniana (3) potrà allora essere riscritta nel modo seguente:

ℋ = − γ ℏI_zH₀; (4)

i suoi livelli di energia, in base a quanto abbiamo detto precedentemente, sono dati da

E = − γℏmH₀. (5)

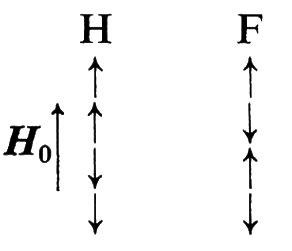
Come esempio vediamo l'unico caso di isotopo stabile dell'ossigeno che può essere osservato, cioè ¹⁷O, che ha I = 5/2. I suoi livelli di energia, per i valori che può assumere m, sono equispaziati a intervalli di energia di ampiezza γℏH₀, come è mostrato nella fig. 1.

Lo studio di una serie di livelli di energia di questo tipo si ottiene inducendo transizioni fra i livelli con onde elettromagnetiche alla frequenza radio, in modo da soddisfare la condizione

ℏω = ΔE, (6)

che rappresenta la conservazione dell'energia. ΔE è la differenza fra le energie del livello finale e di quello iniziale.

La radiazione a radiofrequenza viene trasmessa con una bobina al cui interno è posto il sistema. La bobina è normalmente perpendicolare alla direzione del campo magnetico statico H₀. Il motivo di questa configurazione sarà chiarito più avanti. Le transizioni che possono essere indotte dalla radiofrequenza devono soddisfare la regola di selezione Δm = ± 1. In altre parole, le transizioni possono avvenire soltanto fra livelli energetici adiacenti; di conseguenza

ΔE = ℏω = γℏH₀,

cioè

ω = γH₀. (7)

È importante notare che in quest'ultimo passaggio la costante di Planck ℏ è scomparsa. C'è quindi da aspettarsi che un'analisi fondata sulla meccanica classica, anziché su quella quantistica, porti anch'essa al risultato (7). Infatti vedremo nel prossimo capitolo che la (7) altro non è che la frequenza di precessione di Larmor, ben nota già in meccanica classica.

D'altra parte si può dimostrare in modo rigoroso che l'equazione quantistica che regola la dinamica di un sistema di spins non interagenti (o debolmente interagenti, come quelli dei protoni dell'acqua liquida), cioè l'equazione di Heisenberg, si riconduce a quella classica, cioè alla seconda equazione cardinale. Inoltre le tecniche RMN sperimentali usate attualmente in tomografia e spettroscopia RMN in vivo rivelano soltanto quelle componenti dei tessuti biologici che, come l'acqua, sono attribuibili a spins debolmente interagenti (quest'ultimo aspetto sarà chiarito nella descrizione delle tecniche tomografiche). Da queste due premesse consegue che è perfettamente lecito usare la meccanica classica per interpretare gran parte dei risultati che attualmente vengono ottenuti con la ricerca RMN in vivo

3. La trattazione classica

a) Moto di uno spin isolato.

Un magnete che possieda un momento angolare, se immerso in un campo magnetico H, gli precede intorno. In pratica si comporta come una trottola che, oltre a ruotare intorno al proprio asse, ruota intorno al campo gravitazionale mantenendo con questo un angolo costante, se si trascurano gli effetti degli attriti. Questa conclusione si può facilmente dedurre dalla seconda equazione cardinale

che stabilisce che la derivata rispetto al tempo del momento angolare totale di un sistema (nel nostro caso lo spin nucleare) è uguale alla somma dei momenti delle forze esterne M^(e) agenti sul sistema. In presenza di un campo magnetico, uno spin con momento magnetico μ e momento angolare J è sottoposto a una forza torcente data da μ × H, quindi la (8) diviene, per uno spin isolato,

e, in base alla (1),

Dalla (10) si vede chiaramente che ogni variazione dμ di μ è perpendicolare sia a μ che ad H. Di conseguenza μ si sposta intorno ad H e, se H è indipendente dal tempo, descrive un cono.

Visto che il moto di uno spin è una precessione intorno al campo magnetico, risulta conveniente introdurre, assieme al sistema di riferimento del laboratorio, in cui abbiamo operato fin qui, anche un sistema di riferimento rotante con velocità angolare W. La derivata d/dt di un vettore V rispetto al sistema di laboratorio è legata a quella relativa al sistema rotante δ/δt dalla relazione

La (10) si può allora riscrivere

cioè

La (11) ha esattamente la stessa forma della (10) purché si sostituisca il campo magnetico H che agisce sullo spin con il campo effettivo

È semplice, nel sistema di riferimento rotante, risolvere i casi che più ci interessano. Per esempio, se H è un campo statico e omogeneo che indicheremo con H = H₀ = H₀k, scegliendo il sistema rotante a una velocità angolare W tale che H_e = 0, cioè W = − γH₀k, si avrà dalla (11) δμ/δt = 0. In altre parole lo spin è fermo rispetto al sistema rotante e quindi esso precede, rispetto al laboratorio, a una velocità angolare W = − γH₀k, dove γH₀ è proprio la frequenza di precessione, o di Larmor, (7) già ricavata per via quantistica.

Pensiamo ora di azioniare un campo a radiofrequenza di ampiezza A generato da una bobina solenoidale con asse solidale con l'asse x del sistema di riferimento del laboratorio. Questa radiazione, che è polarizzata linearmente lungo l'asse x, può essere scomposta nella somma di due componenti di eguale ampiezza polarizzate circolarmente, una in senso orario e l'altra in senso antiorario. Solo una delle due componenti di questa radiazione sarà attiva nell'interazione con gli spins e quindi potremo scrivere il campo che ci interessa come

H₁ = H₁(i cos ωt ± j sen ωt), (13)

dove H₁ = A/2 e i segni ± si riferiscono alle due componenti. L'effetto di un campo magnetico statico H₀ = H₀k e di H₁ in un sistema di riferimento rotante intorno all'asse z alla frequenza ω della radiazione è dato da

dove i′ è il versore dell'asse x′ del sistema rotante nel quale H₁ è statico; fra le due componenti della radiofrequenza polarizzata circolarmente è stata scelta quella con segno tale che in risonanza porta a γH₀ − ω = 0, cioè ω = ω₀ ≡ γH₀. La (14) si può riscrivere

con

La (15) significa che nel sistema rotante il momento magnetico (spin) evolve come se fosse sottoposto a un campo magnetico statico H_e. Di conseguenza, nel sistema rotante, lo spin precede intorno ad H_e alla frequenza costante γH_e. La situazione è chiarita nella fig. 2.

Se inizialmente μ è orientato lungo la direzione z del campo magnetico statico H₀, se ne allontana ritornandovi periodicamente a causa del suo moto di precessione. In condizioni di risonanza si ha ω₀ = γH₀ e il campo efficace è H_e = i′H₁; di conseguenza lo spin, inizialmente lungo z, ruota nel piano (z, y′) sempre perpendicolarmente ad H₁, e periodicamente si troverà diretto nel verso di H₀ e nel verso opposto. Se l'azione della radiazione si interrompe dopo un tempo τ, il momento magnetico che precede alla frequenza angolare γH₁ avrà percorso un angolo θ = γΗ₁τ. Un impulso tale che, scegliendo opportunamente H₁ e τ, dia θ= π/2 è detto di 90°; se θ = π, l'impulso è detto di 180° in quanto il suo effetto è quello di ruotare il momento magnetico di 180°, cioè di invertirne il verso. L'effetto di un impulso di 90° è quello di portare il momento magnetico dalla direzione di equilibrio z a quella y′ nel sistema rotante. Nella direzione y′ lo spin è statico e quindi di fatto esso ruota nel sistema del laboratorio alla frequenza ω₀ nel piano (x, y). La bobina, coassiale con x, viene normalmente utilizzata, dopo l'interruzione di H₁, per rivelare la forza elettromotrice che il moto del momento magnetico genera ai suoi capi. Questo segnale in funzione del tempo è generalmente chiamato FID (Free Induction Decay). Se gli spins fossero effettivamente non interagenti e H₀ perfettamente omogeneo, il segnale FID non dovrebbe attenuarsi. A causa delle interazioni fra gli spins, invece, il segnale ovviamente decade e torna all'equilibrio con costanti di tempo caratteristiche. La trasformata di Fourier della FID dà lo spettro RMN in funzione della frequenza.

b) L'equazione di Bloch.

Quando invece che di un singolo spin si tratta di un sistema di spins uguali, piuttosto che di momento magnetico si parla di magnetizzazione macroscopica M, che è il risultato statistico del contributo di tutti i singoli momenti magnetici, ciascuno con orientamento relativo ad H₀ dipendente dal livello di energia in cui si trova (v. fig. 1). In pratica è proprio M la grandezza che sperimentalmente viene determinata e a essa si applicano tutte le equazioni scritte fin qui per μ.

L'equazione di Bloch, che permette di calcolare l'evoluzione di M, si scrive

dove H è il campo magnetico totale, M_x, M_y, M_z sono ovviamente le componenti di M, T₂ è il tempo di rilassamento spin-spin e T₁ il tempo di rilassamento spin-reticolo. In pratica l'equazione di Bloch è ancora la seconda equazione cardinale, in cui al momento della forza esterna causata da H si aggiungono due forze fenomenologiche dissipative che descrivono lo smorzamento della FID e il ritorno all'equilibrio termodinamico del sistema di spins quando l'azione della radiofrequenza è cessata.

Dopo un impulso di 90° la magnetizzazione si trova nel piano (x′, y′) del sistema rotante in cui è statica. Se l'impulso è di durata molto minore di T₁ e T₂, l'ampiezza della magnetizzazione nel piano (x′, y′) è praticamente identica a quella di equilibrio M₀ prima dell'impulso (M = M₀k). I diversi campi locali H_loc prodotti dai singoli spins sugli spins vicini fanno sì che ogni spin sia sottoposto a un campo totale dato dalla somma H₀ + H_loc. Di conseguenza ciascuno spin avrà una frequenza di precessione diversa dagli altri e la risultante M₀ del contributo statistico di tutti gli spins comincerà a smorzarsi (v. fig. 3) a causa di una perdita di coerenza nel loro moto di precessione. In sostanza quindi è l'interazione spin-spin a causare lo smorzamento della componente trasversale di M con la costante di tempo T₂. Valori tipici di T₂ variano dai secondi, nei liquidi, ai microsecondi, nei solidi.

Il ritorno all'equilibrio termodinamico corrisponde invece alla ricostituzione di M₀ lungo z. Questo processo coinvolge uno scambio di energia con il ‛reticolo', cioè il bagno termico, ed è causato dall'interazione spin-reticolo. Il reticolo è di fatto il sistema di atomi e molecole in moto di cui fanno parte gli spins.

L'equazione di Bloch (17) prevede che dopo l'azione di un impulso a radiofrequenza, quando cioè il momento delle forze esterne è nullo, il ritorno all'equilibrio della componente trasversale (x, y) e di quella longitudinale (z) sia esponenziale, con T₂ e T₁ costanti di tempo rispettive. Naturalmente questi due parametri sono fondamentali per lo studio della dinamica molecolare da cui essi dipendono. In generale T₂ ≤ T₁.

c) La sequenza spin-eco.

La coerenza del moto degli spins su scale di tempo inferiori a T₂ consente di applicare numerose sequenze di impulsi a radiofrequenza, imponendo al sistema di spins una dinamica prescelta per ottenere successivamente l'informazione fisica voluta dal segnale RMN in funzione del tempo. Una sequenza semplice ma di grande importanza per le applicazioni biomediche è la cosiddetta sequenza spin-eco (v. Hahn, 1950). La sua importanza attuale è legata al fatto che essa costituisce la base di gran parte delle procedure tomografiche oggi applicate in campo biomedico. La sequenza spin-eco è costituita da due impulsi, il primo, di 180°, che inverte la direzione della magnetizzazione, e il secondo, applicato dopo un tempo t₀, di 90°. Questa sequenza si applica quando la disomogeneità del campo statico H₀ è tale da far perdere l'allineamento agli spins nel piano (x, y) in un tempo T₂* 〈 T₂. La disomogeneità ha in generale una distribuzione spaziale che non cambia nel tempo, pertanto uno spin (se i moti diffusivi sono lenti) esperimenta un campo statico diverso da H₀. Una situazione simile si ha in tomografia, dove la disomogeneità si introduce di proposito con l'aggiunta di gradienti di campo magnetico per motivi che saranno chiariti più avanti.

La disomogeneità in H₀ fa sì che, dopo l'impulso di 90° (v. fig. 4A), nel piano (x′, y′) del sistema rotante gli spins sottoposti a campo magnetico leggermente inferiore ad H₀ restino più indietro e quelli sottoposti a campo maggiore di H₀ vadano più avanti (v. fig. 4B) di quanto farebbero nel campo omogeneo H₀. L'applicazione di un impulso a 180° dopo un tempo t₀ 〈 T₂ ribalta solo la componente y′ delle componenti sparpagliate, per cui i due vettori m e n verranno ruotati in m′ e n′ (v. fig. 4C); m′ e n′ formano gli stessi angoli θ e θ′ con l'asse y′ per cui, precedendo alla stessa velocità angolare di prima, ma, in C, avvicinandosi a y′, invece di allontanarsene come in B, finiscono per ricomporsi dopo un tempo 2t₀ = T_E e generare quindi un segnale di massima intensità (v. fig. 4D).

La sequenza con il segnale generato è mostrata nella fig. 5. Questa sequenza viene usata per misurare T₂. Il decadimento della FID e la forma dell'eco nella fig. 5 sono determinati dalle disomogeneità di campo. Il decadimento del segnale dovuto a T₂ è invece dato dall'inviluppo dei massimi di tutti gli echi ottenuti con ogni possibile t₀.

4. Le basi fisiche della tomografia RMN

a) Aspetti generali.

Avendo visto fin qui i principî elementari della RMN, è possibile comprendere le basi fisiche su cui si fonda la tomografia RMN.

In ogni tecnica di indagine basata sull'invio di una sonda nel sistema da studiare si deve cercare di minimizzare l'effetto della perturbazione prodotta dalla sonda sul sistema. La minimizzazione dell'effetto perturbativo è ancora più importante nello studio dei sistemi viventi come l'uomo, perché in tal caso un elevato livello di perturbazione, a prescindere dalla scarsa qualità dei risultati, può provocare un danno all'organismo. Per questo motivo, fra le molte sonde spettroscopiche, sono preferibili quelle che implicano minori energie e intensità. Per esempio, rispetto ai raggi X, la cui energia è capace di ionizzare atomi e molecole e quindi di produrre danni di vario genere, sono preferibili le onde elettromagnetiche alle frequenze radio (approssimativamente da 2 a 80 MHz) attualmente usate per l'indagine biomedica sull'uomo in vivo nella RMN, la cui energia (per fotone) è approssimativamente 10¹⁰ volte più piccola.

I corpi viventi sono eterogenei sia su scala macroscopica, per la struttura a organi, sia a livello cellulare e tessutale. Di conseguenza anche la distribuzione dei nuclei con momento magnetico, come ad esempio il protone degli atomi di idrogeno dell'acqua, ha una ripartizione spaziale che, se rivelata, deve mostrare le strutture morfologiche. Inoltre, l'informazione spettroscopica dei nuclei contenuti in un piccolo elemento di volume dovrebbe fornire informazioni biochimiche sui processi che avvengono su scala molecolare. Questo elemento di volume dovrebbe essere più piccolo possibile in modo da minimizzare gli effetti dell'eterogeneità e ottimizzare la risoluzione. Normalmente i metodi di indagine capaci di fornire dati fisici in funzione della posizione, cioè delle coordinate spaziali, all'interno di un corpo vivente vengono denominati ‛tomografie'. Una tomografia fornisce una mappa in due (o in tre) dimensioni di un parametro fisico o di una funzione di più parametri appartenenti a uno strato di un corpo vivente. La mappa bidimensionale, o meglio la matrice, in quanto e costituita da un numero finito di elementi, è quanto noi normalmente chiamiamo ‛immagine' di uno strato di un corpo. Un esempio ben noto di tomografia è la tomografia a raggi X (TAC, tomografia assiale computerizzata), ma ne esistono altre quali la PET (Positron Emission Tomography; v. tomografia a emissione di positoni, suppl.), la SPECT (Single Photon Emission Computerized Tomography) e infine la tomografia a risonanza magnetica nucleare (talvolta chiamata MRI, Magnetic Resonance Imaging: v. tomografia a risonanza magnetica nucleare, suppl.). Deve essere ben chiaro quindi che tomografia o imaging significano di fatto spettroscopia di un sistema eterogeneo. Questo è particolarmente vero per la RMN, in quanto con le varie tecniche tomografiche è possibile ricavare mappe bio tridimensionali di ciascuno dei molti parametri che la spettroscopia RMN consente di misurare.

L'applicazione della RMN a tessuti di organismi viventi, cioè in vitro, è vecchia quasi quanto la RMN stessa, mentre l'origine delle sue applicazioni biomediche risale all'inizio degli anni settanta. Infatti nel 1971 R. Damadian (v., 1971 ) trovò che uno dei classici parametri RMN, cioè il tempo di rilassamento spin-reticolo, T₁, era più lungo nel tessuto canceroso che in quello sano dello stesso organo. Quindi la possibilità di discriminare con un parametro spettroscopico RMN un tessuto patologico da uno sano, aggiunta allo sviluppo dei metodi tomografici avvenuto in quegli anni, portò più ricercatori a indagare su procedure sperimentali per ottenere immagini con RMN. Il primo ad aver successo fu P. Lauterbur (v., 1973) a Stony Brook. La rivelazione di segnali RMN risolti nello spazio realizzata da Lauterbur si fondava su un'idea molto semplice. La RMN tradizionale fa uso di bobine che contengono il campione da studiare e che servono sia per trasmettere le onde elettromagnetiche a radiofrequenza sia per rivelare il segnale RMN, cioè la FID. Tutta la parte del campione contenuta nella bobina, immersa nel campo magnetico statico e omogeneo H₀, genera un segnale centrato alla frequenza

ω₀ = γH₀ (18)

secondo la relazione (7). Ogni spin, cioè, trovandosi immerso nello stesso campo H₀, precede alla stessa frequenza ω₀. Il contributo di tutti gli spins quindi si trova alla stessa frequenza (se si trascura naturalmente l'interazione spin-spin che produce un H_loc normalmente molto più piccolo di H₀). Lo spettro che dà l'intensità del segnale in funzione della frequenza non ci permette di conseguenza di distinguere il contributo degli spins che appartengono a un certo volume dal contributo degli spins che appartengono a un altro. Nel caso dei sistemi omogenei, che di solito si studiano in fisica, questo non è importante, ma per discriminare spazialmente il contributo degli spins localizzati in zone diverse si deve utilizzare un artificio. L'artificio proposto da Lauterbur è un debole gradiente costante di campo magnetico G sovrapposto ad H₀. Il gradiente introduce infatti una dipendenza spaziale del campo magnetico totale nella direzione di G. In ogni piano individuato dal vettore r ci sarà quindi un campo magnetico totale di intensità

H = H₀ + G • r. (19)

La frequenza di risonanza degli spins contenuti in tale piano sarà quindi data da

ω = γH = γ(H₀ + G • r), (20)

che mostra come ogni piano corrispondente a un valore di r possieda una frequenza ω diversa. La distribuzione delle frequenze di risonanza diventerà allora la distribuzione della posizione degli spins nello spazio. Pensiamo, come esempio, di introdurre alcune provette contenenti acqua (e quindi protoni con spin 1/2) parallele fra loro e formanti una F (v. fig. 6) all'interno della bobina RMN. In presenza del solo H₀ gli spins dei protoni risuoneranno tutti alla stessa frequenza ω₀ = γH₀. Sommando invece ad H₀ il campo relativo al gradiente costante G (v. eq. 19), il campo magnetico totale varierà linearmente lungo la direzione di G. Di conseguenza l'intensità del segnale in funzione della frequenza fornirà la distribuzione delle densità dei protoni lungo G. Praticamente quindi lo spettro ottenuto è una proiezione del contenuto d'acqua dei piani perpendicolari a G, come è mostrato nella fig. 6.

Se si varia la direzione del gradiente G, si ottengono proiezioni diverse dello stesso campione, analogamente a quanto si fa con la TAC (v. radiologia medica). Anche la procedura di ricostruzione dell'immagine a partire dalle proiezioni è molto simile a quella usata per la TAC o altre tomografie si tratta del metodo proiezione-ricostruzione (PR) proposto inizialmente da Lauterbur nel 1973. Successivamente sono stati suggeriti diversi altri metodi, tutti facenti uso di gradienti di campo magnetico, ma con procedure molto diversificate e con risultati talvolta di notevole interesse e talaltra validi solo in linea di principio. Fra questi quello di maggior successo, attualmente adottato in modo praticamente universale, è il metodo della trasformata di Fourier proposto da Ernst (v. Kumar e altri, 1975). Le sue basi fisiche e la relativa procedura saranno descritte nel prossimo paragrafo.

Un'altra famiglia di metodi per ottenere immagini RMN è fondata sul principio dell'irraggiamento selettivo. Questo multiforme gruppo di metodi, fra i quali possiamo includere l'eco planare, che attualmente è la procedura più rapida esistente, è stato introdotto da P. Mansfield (v. Mansfield e Morns. 1982). Irraggiamento selettivo significa irraggiare un campione con uno spettro di frequenze particolari, in modo da eccitare solo gli spins di alcune zone prescelte del campione in presenza di gradienti di campo magnetico. Per questo si utilizzano impulsi a radiofrequenza con profili spettrali sagomati in modo opportuno. Infatti lo spettro di eccitazione associato all'impulso è dato dalla trasformata di Fourier dell'impulso stesso; quindi per fare in modo che siano presenti solo le componenti spettrali desiderate, si modula nel tempo l'ampiezza dell'impulso con una funzione che è l'antitrasformata di Fourier del profilo spettrale voluto. Come esempio vediamo il caso più semplice e più usato di irraggiamento selettivo, cioè la selezione di uno strato prescelto del quale si intende ottenere l'immagine con il metodo spin warp o proiezione-ricostruzione. Se durante l'irraggiamento si applica un gradiente di campo magnetico G_z nella direzione z (ma qualunque direzione è equivalente), la composizione spettrale minima necessaria per eccitare tutti gli spins del corpo immerso nel campo H₀ deve contenere l'intervallo di frequenza Δω = γG_z • Z, dove Z è la lunghezza del corpo contenuto in H₀. Se invece l'impulso a radiofrequenza contiene solo un intervallo di frequenza Δω′ all'interno di Δω e tale che Δω′ ≪ Δω, gli spins che vengono eccitati saranno solo quelli contenuti nello strato perpendicolare a z, nel quale gli spins precedono alle frequenze contenute in Δω′. Naturalmente i metodi di irraggiamento selettivo comportano procedure più complesse, ma attualmente non vengono utilizzati.

b) Fondamenti teorici.

Per poter analizzare i metodi tomografici RMN (capirne il potenziale nonché l'accuratezza con cui generano le distribuzioni spaziali dei parametri RMN) è necessario prima di tutto conoscere i fondamenti teorici sui quali si basano. Questi fondamenti non sono altro che l'equazione di Bloch (17), che dovrà però essere applicata a sistemi eterogenei; infatti, per ricavare gli spettri RMN, in generale è necessario calcolare l'evoluzione nel tempo della magnetizzazione M e farne la trasformata di Fourier. Dato che i sistemi biologici sono eterogenei, la magnetizzazione e i tempi di rilassamento cambiano punto per punto, cioè M e le sue componenti, M₀, T₁ e T₂ dipendono dalle coordinate r ≡ x, y, z. Se chiamiamo S(t) la funzione che rappresenta la FID (e quindi rappresenta anche l'eco, che può essere considerato come la somma di due FID, una crescente fino al massimo e l'altra calante), la soluzione dell'equazione di Bloch per sistemi eterogenei, come dimostrato da De Luca e altri (v., 1986), è data da

dove m₀(r_G) è la magnetizzazione di equilibrio dovuta agli spins risonanti del piano ortogonale al gradiente G e individuato dalla coordinata r_G, T₂(r_G) è il valore di T₂ mediato su tutti gli spins risonanti dello stesso piano, L_G è la massima estensione del campione nella direzione di G, t = 0 corrisponde alla fine dell'impulso di eccitazione a radiofrequenze, t₁ è l'istante in cui viene acceso G e naturalmente ω₀ = γH₀ è la frequenza di Larmor. L'equazione (21) contiene praticamente tutta l'informazione che in generale serve per poter prevedere la risposta e la validità dei metodi tomografici. Sia il metodo proiezione-ricostruzione che quello spin warp altro non sono che casi particolari della (21), per i quali la variante è soprattutto nell'integrale all'esponente che, a seconda della procedura di eccitazione, codifica gli spins nel modo prescelto.

Per il metodo proiezione-ricostruzione, infatti, si ha che G = costante, per cui l'integrale nell'esponente della (21) ha la semplice soluzione r • Gt. In questo caso lo spettro in frequenza, cioè la trasformata di Fourier della FID data dalla (21), è una sovrapposizione di lorentziane, ciascuna centrata sulla frequenza ω₀ + γr • G. Questa sovrapposizione è proprio la proiezione del corpo nella direzione di G. È necessario, come già detto, un numero finito di proiezioni con diverse direzioni di G per poter ricostruire l'immagine. Se abbiamo preventivamente selezionato un piano, la ricostruzione sarà in due dimensioni; in generale però questo metodo può essere applicato in tre dimensioni, anche se, ovviamente, richiede un tempo di acquisizione molto maggiore.

Il metodo spin warp, oggi ampiamente usato con notevole successo, merita particolare attenzione. Anche per questo metodo ci limitiamo al caso bidimensionale, cioè associato alla selezione di un certo strato con irraggiamento selettivo, pur essendo lo spin warp semplice da utilizzare per immagini tridimensionali. Questo metodo è una modifica della zeugmatografia di Fourier (v. Kumar e altri, 1975), nella quale si opera sulla fase degli spins attraverso l'integrale nell'esponente della (21). In pratica si fanno agire dei gradienti G costanti e si varia il tempo t a passi discreti. La trasformata di Fourier del segnale produce direttamente l'immagine bi- o tridimensionale senza necessità di usare algoritmi tradizionali di ricostruzione. Il metodo spin warp arriva allo stesso risultato con una procedura un po' diversa e tecnicamente più semplice da realizzare. In sostanza l'azione dei gradienti è fatta esercitare su un intervallo di tempo sempre uguale, mentre viene variata a intervalli fissi l'ampiezza del gradiente. Così il valore dell'integrale nell'esponente della (21) può assumere gli stessi valori che assume nella zeugmatografia di Fourier variando per gradi l'ampiezza di G a intervalli di tempo costante invece che variando gli intervalli di tempo a G costante.

Per meglio comprendere questo importante metodo si vedano i dettagli della sequenza base (spin-eco) usata in quasi tutte le procedure di acquisizione e mostrata nella fig. 7. Gli impulsi a radiofrequenza (90° e 180°) sono modulati in ampiezza in modo da avere la composizione spettrale prescelta per irraggiare selettivamente uno strato (x, y); infatti durante l'irraggiamento viene anche acceso il gradiente G_z, in modo che ogni frequenza ecciti gli spins contenuti in un piano (x, y). Dopo il primo impulso a radiofrequenza si ha il segnale RMN dato dalla FID, che però non viene letto, in quanto non contiene ancora quella codifica che vogliamo introdurre con il gradiente G_z. Immediatamente dopo l'impulso selettivo di 90° vengono accesi i gradienti G_y e G_x con un'ampiezza prescelta, ma entrambi per un intervallo di tempo che non viene cambiato, almeno durante l'acquisizione di un'immagine. Successivamente si applica un impulso selettivo a 180° e infine il solo gradiente G_y (per questo detto ‛di lettura') per tutto il tempo necessario ad acquisire il segnale RMN (eco). L'intera procedura viene ripetuta in modo identico 128 o 256 volte, cambiando ogni volta l'ampiezza di G soltanto di un gradino. Infine la trasformata di Fourier bidimensionale del quadro di acquisizione effettuato produce l'immagine tomografica. È facile introdurre un contrasto in T₁ su un'immagine acquisita con questa sequenza. Nell'acquisizione degli echi si può, ad esempio, usare un tempo di ripetizione T_R 〈 T₁; oppure basta applicare un impulso di 180° prima della sequenza spin-eco, in modo da avere la sequenza inversion-recovery. Naturalmente l'intervallo di tempo fra il primo impulso di 180° e la sequenza spin-eco deve essere comparabile con T₁. Le immagini nelle figg. 8, 9, 10 e 11, ottenute con sequenze spin-eco, mostrano l'attuale livello raggiunto da questa particolare procedura.

c) Apparato sperimentale.

L'apparato sperimentale utilizzato per la ricerca RMN in vivo differisce solo per alcuni aspetti dagli spettrometri a impulsi di potenza usati per misure di tempi di rilassamento e di forme di riga nei solidi. Nello schema a blocchi mostrato nella fig. 12 si vede innanzitutto il paziente all'interno di un magnete formato da quattro grandi bobine. Si tratta di un magnete resistivo utilizzato per tomografi a basso campo (0,1 ÷ 0,2 T). Valori di campo analoghi possono essere ottenuti con magneti permanenti, con il vantaggio di un minor costo d'esercizio. I magneti permanenti stanno avendo attualmente un notevole sviluppo in questo settore. Per campi magnetici superiori è necessario l'uso di magneti superconduttori che vengono utilizzati fino a 2 T per la ricerca e la diagnostica sull'uomo. Questi magneti hanno il vantaggio di una maggiore stabilità nel tempo e di una migliore omogeneità. Il loro costo d'esercizio è però più elevato. Valori di campo superiori superano le linee guida applicate in quasi tutto il mondo occidentale e per questo vengono usati solo per ricerche su animali. Il magnete è corredato di bobine per i gradienti e della bobina per la radiofrequenza (v. fig. 13). L'intero sistema è schermato da una gabbia di Faraday per eliminare tutti i possibili disturbi a radiofrequenza provenienti dall'esterno. Lo strumento è naturalmente controllato da un calcolatore che determina le sequenze, le forme d'onda per l'irraggiamento selettivo, l'acquisizione dei dati e la loro elaborazione per produrre l'immagine.

Questi apparati naturalmente possono essere corredati di bobine di molti tipi (a sella, a ellissi incrociate, superficiali, ecc.) a seconda della parte del corpo a cui si è interessanti.

Con l'espressione ‛spettroscopia in vivo' nel gergo corrente ci si riferisce allo studio di spettri caratterizzati in genere dallo spostamento chimico (v. risonanza magnetica nucleare: Applicazioni chimiche, suppl.) e rivelati direttamente in vivo in un comparto del corpo. In realtà ogni misura RMN, anche tomografica, è spettroscopia. Per ragioni di convenienza comunque ci atterremo al gergo comune.

Per gli studi spettroscopici in vivo (v. risonanza magnetica nucleare: Applicazioni biochimiche e biologiche, suppl.; v. tomografia a risonanza magnetica nucleare, suppl.) il metodo sperimentale ancora prevalente fa uso di bobine superficiali, capaci di rivelare segnali locali (in genere a profondità pari al raggio delle bobine) per le loro dimensioni limitate. In pratica, cioè, la loro risoluzione spaziale è affidata alle loro dimensioni e non a procedure tomografiche. La loro localizzazione può essere migliorata irradiando con impulsi selettivi o con sequenze più raffinate (ormai innumerevoli). Più in generale è anche possibile ottenere mappe dello spostamento chimico, cioè ottenere per ciascun pixel (picture element: ‛elemento d'immagine') lo spettro con i relativi picchi. Il limite di questa tecnica sta nel fatto che i tempi di acquisizione sono molto elevati. In generale per massimizzare il rapporto segnale/rumore si opera a campi elevati.

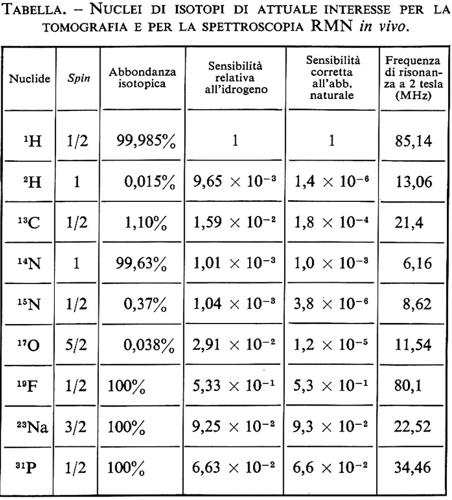
La spettroscopia in vivo può essere realizzata anche ai campi bassi prodotti da un magnete resistivo, se il nucleo a cui si è interessati è il nucleo dell'atomo di idrogeno, che peraltro è molto abbondante. È possibile in questo modo ottenere i picchi prodotti dal protone degli atomi di idrogeno dell'acqua e di quelli dei lipidi. Per ottenere spettri di altri nuclei, come ³¹P, ¹³C, ²³Na, ecc. (v. tabella), è necessano operare a campi superiori a 1 T. Il nucleo più studiato è certamente il ³¹P. Infatti, a differenza del protone, che appartiene a un numero molto grande di composti, il fosforo produce uno spettro semplice e di facile interpretazione.

Lo spettro del ³¹P di un muscolo è riportato schematicamente nella fig. 14. Sulle ascisse i numeri indicano gli spostamenti chimici in parti per milione, relativi al picco della fosfocreatina (PCr). I picchi indicati con α, β e γ sono dovuti all'ATP. Il picco P_i è dovuto al fosforo inorganico, quello P_s ai fosfomonoesteri. Uno degli aspetti impoatanti è che lo spostamento chimico del fosforo inorganico (P_i) cambia con il pH, di conseguenza è possibile misurano direttamente in vivo.

Ovviamente le variazioni dell'intensità relativa dei picchi (cioè delle loro aree) dipendono dalle concentrazioni dei composti e per questa via è possibile studiare gli equilibri chimici direttamente. Variazioni dovute a fattori patologici o all'azione di farmaci saranno oggetto della ricerca futura. Al momento questo settore è in fase di decollo, ma grandemente limitato da fattori tecnici che rendono le misure quantitative molto difficili e finora poco affidabili.

d) Sviluppi recenti.

Lo studio dei flussi idrodinamici, come quello del sangue, sta dando risultati sempre più interessanti. Fra i primi risultati in vivo di rilievo, quelli ottenuti da Singer e Crooks (v., 1983) mostrano la quantità di informazione che si può dedurre, come ad esempio la portata e la velocità di flusso in un vaso. È importante notare che questo tipo di studio non richiede una strumentazione apposita, ma solo delle sequenze di impulsi e dei metodi di analisi diversi applicati alle procedure tomografiche.

Fra le altre grandi linee di sviluppo c'è quella dei mezzi di contrasto. Questo tema è ben noto in radiologia e per la TAC. Infatti i raggi X attraversano i tessuti molli, che formano gran parte dei nostri organi, senza apprezzabile attenuazione. Per questo si ingeriscono o si iniettano sostanze contenenti atomi pesanti in modo da contrastare la parte desiderata. Per la RMN il contrasto deve operare sui parametri tipici quali T₁ e T₂. L'introduzione di sostanze paramagnetiche, ferromagnetiche o comunque con caratteristiche tali da modificare i tempi di rilassamento può generalmente aumentare il contrasto nelle immagini.

È molto importante una nuova possibilità che si offre attualmente al ricercatore e che consiste nell'individuare molecole che abbiano affinità specifica per determinate forme patologiche (specifiche ad es. per un tumore). Queste sostanze, una volta marcate con gruppi paramagnetici, non solo metterebbero in risalto in tomografia a RMN la parte patologica fino a dimensioni dell'ordine del millimetro, ma, grazie alla loro specificità, permetterebbero di determinare in modo univoco di quale patologia si tratta. Le stesse sostanze potrebbero naturalmente essere marcate con isotopi radioattivi e analizzate con tomografia γ. Il limite di quest'ultima tecnica è però il suo modesto potere risolutivo.

Come è già stato detto nella descrizione dell'irraggiamento selettivo, metodi tomografici molto veloci, capaci cioè di produrre immagini in tempo reale, già esistono. È necessario però svilupparne la qualità o progettare metodi nuovi e più efficienti in modo da ottenere immagini di buon livello. Un successo in questa direzione sarebbe di enorme importanza in campo cardiologico, perché consentirebbe una visualizzazione diretta del cuore durante la sua naturale dinamica.

Fra le molte linee di sviluppo è infine di grande rilievo quella che viene chiamata microscopia RMN. Se nei tomografi attualmente a disposizione degli ospedali si arriva a poteri risolutivi poco inferiori al millimetro, ciò non significa che non sia possibile risolvere spazialmente sistemi di dimensioni inferiori a quelli di una cellula. In particolare, operando a campi magnetici elevati e su oggetti di piccole dimensioni, è possibile da tempo raggiungere poteri risolutivi dell'ordine di qualche decina di micrometri. Recentemente è stata pubblicata la prima immagine RMN di una cellula (anche se di grandi dimensioni): si tratta dell'immagine di un uovo ottenuta con potere risolutivo intorno a 10 μm (v. fig. 15; v. Aguayo e altri, 1986).

BIBLIOGRAFIA

Abragam, A., The principles of nuclear magnetism, Oxford 1971.

Aguayo, J.B., Blackband, S.J., schoeniger, J., Mattingly, M. A., Hintermann, M., Nuclear magnetic resonance imaging of a single cell, in ‟Nature", 1986, CCCXXII, pp. 190-191.

Bloch, F., Hansen, W.W., Packard, M., The nuclear induction experiment, in ‟Physical review", 1946, LXX, pp. 460-474.

Damadian, R., Tumor detection by nuclear magnetic resonance, in ‟Science", 1971, CLXXI, pp. 1151-1153.

De Luca, F., De Simone, B.C., Maraviglia, B., Campanella, R., Casieri, C., The physical basis of NMR tomography, in NATO Advanced Study Institute on NMR in living systems, 1984, ASI series C, 1986, vol. CLXIV, pp. 109-116.

Gorter, C. J., Broer, L. J. F., Negative result of an attempt to observe nuclear magnetic resonance in solids, in ‟Physica", 1942, IX, pp. 591-596.

Hahn, E.L., Spin echoes, in ‟Physical review", 1950, LXXX, pp. 580-594.

Kumar, A., Welti, D., Ernst, R.R., NMR Fourier zeugmatography, in ‟Journal of magnetic resonance", 1975, XVIII, pp. 69-83.

Lauterbur, P., Image formation by induced local interactions: examples employing nuclear magnetic resonance, in ‟Nature", 1973, CCXLII, pp. 190-191.

Mansfield, P., Morris, P.G., NMR imaging in biomedicine, Suppl. 2, in Advancs in magnetic resonance, New York 1982.

Purcell, E. U., Torrey, H.C., Pound, R.V., Resonance absorption by nuclear magnetic moment in a solid, in ‟Physical review", 1946, LXIX, pp. 37-38.

Rabi, I.I., Space quantization in a gyrating magnetic field, in ‟Physical review", 1937, CI, pp. 652-654.

Singer, J.R., Crooks, L.E., Nuclear magnetic resonance blood flow measurement in the human brain, in ‟Science", 1983, CCXXI, pp. 654-656.

Applicazioni chimiche di Filippo Conti

SOMMARIO: 1. Introduzione.  2. Parametri fondamentali degli spettri RMN.  3. Spettrometri per RMN.  4 Composti organici.  5 Composti paramagnetici.  6. Polimeri sintetici.  7. Alcune applicazioni chimico-fisiche: a) studi termodinamici; b) studi strutturali; c) studi cinetici. □ Bibliografia.

1. Introduzione.

L'impiego dell'RMN nella chimica è tra i più ampi e diversificati, spaziando dalla chimica analitica alla chimica fisica, alla chimica organica e inorganica. Una rassegna, sia pure sommaria, sull'argomento è oltremodo difficoltosa, anche perché molti risultati sono riportati in articoli i cui titoli non contengono un esplicito riferimento spettroscopico: sono comunque reperibili raccolte di dati continuamente aggiornate per molte classi di composti, come steroidi, zuccheri, peptidi.

La caratterizzazione strutturale di una molecola è presupposto imprescindibile per ogni Studio di carattere chimico. Essa è basata sulla conoscenza del peso molecolare, della formula di struttura, della configurazione e della conformazione della molecola.

Una corretta e sistematica metodologia di interpretazione degli spettri RMN non può prescindere, in primo luogo, dalla perfetta conoscenza delle condizioni chimico-fisiche di ottenimento degli spettri e, successivamente, dal valore dei parametri caratteristici dell'RMN.

2. Parametri fondamentali degli spettri RMN.

Uno spettro RMN è caratterizzato da cinque parametri fondamentali: I) intensità e area dei segnali; 2) valore delle frequenze di risonanza, chiamato ‛spostamento chimico' o chemical shift, indicato con δ e misurato in hertz (Hz) o in parti per milione (ppm); 3) costanti di accoppiamento tra spins nucleari, indicate con J e misurate in hertz; 4) tempo di rilassamento longitudinale o spin-reticolo, indicato con T₁ e misurato in secondi; 5) tempo di rilassamento trasversale o spin-spin, indicato con T₂ e misurato in secondi.

Intensità e area dei segnali. - In generale l'intensità di un segnale di risonanza di una specie nucleare è proporzionale alla sua concentrazione ed è anche funzione dello stato fisico del sistema che si esamina, il quale influenza i processi di ritorno all'equilibrio delle componenti della magnetizzazione dopo l'impulso e quindi lo spettro che ne è la rappresentazione. Ciò comporta che per la valutazione della concentrazione delle specie nucleari occorre esaminare l'area del segnale di risonanza piuttosto che la sua intensità.

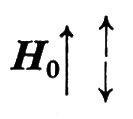
Spostamento chimico o chemical shift. - In presenza di un campo magnetico di intensità data, elementi diversi (¹H, ¹³C, ¹⁹F, ³¹P, ecc.) o isotopi dello stesso elemento (¹H e ²H, ¹⁴N e ¹⁵N, ecc.) assorbono energia, cioè entrano in risonanza, a diversi valori di frequenza, a causa del diverso valore del rapporto giromagnetico Tuttavia anche per una stessa specie isotopica (ad es. ¹H) si possono avere valori di frequenza di risonanza diversi. Utilizzando campi maguetici molto omogenei (ΔH₀/H₀ ≤ 10^-9) i due protoni dell'acqua risuonano a frequenze diverse da quelli dell'etanolo, CH₃CH₂OH. In quest'ultimo i protoni del gruppo CH₃ hanno una frequenza di risonanza diversa da quella dei protoni del gruppo CH₂ e ancora diversa da quella dei protoni del gruppo OH (v. fig. 1). La spiegazione di questa variazione delle frequenze di risonanza dell'idrogeno può essere ottenuta considerando la situazione elettronica degli atomi che formano le molecole. Il campo magnetico H₀ fa sentire la sua influenza sul nucleo ma anche sull'elettrone. Ciò determina l'induzione di un campo magnetico, H_indotto, tale da opporsi al campo magnetico applicato, H₀ (v. fig. 2). Il valore del campo magnetico indotto è proporzionale al campo magnetico che lo induce, H_indotto = H₀(1 − σ), dove σ è una costante adimensionale (‛costante di schermo' o ‛costante di shielding'). Essa dipende da tutti i fattori che influenzano il contorno chimico del nucleo in esame. Così, ad esempio, nelle molecole σ dipende dall'elettronegatività degli atomi legati o immediatamente vicini al nucleo in esame. Le diverse frequenze di risonanza dei protoni dell'acqua e dell'etanolo trovano spiegazione nel diverso schermaggio elettronico dei nuclei ¹H nei vari gruppi chimici.

Altri fattori che possono influenzare la costante di schermo, e quindi la frequenza di risonanza, riguardano le caratteristiche chimico-fisiche del campione e le condizioni sperimentali in cui si opera, quali la concentrazione del campione, il pH, il solvente, la temperatura, ecc.

La costante di schermo e quindi la frequenza di risonanza possono essere influenzate anche da effetti a distanza dovuti alla presenza di gruppi con anisotropia magnetica. Tali effetti dipendono dalla disposizione spaziale degli atomi nella stessa molecola o in molecole diverse. Così nelle due conformazioni possibili delle ammidi (v. fig. 3) il protone del gruppo NH ha frequenze di risonanza diverse.

Effetti analoghi sono dati da anelli aromatici, legami insaturi e, come nel caso dei protoni assiali ed equatoriali del cicloesano, anche da legami C−H in sistemi rigidi. Il chemical shift può anche essere influenzato dalla presenza di centri paramagnetici, come si vedrà in seguito.

Lo spostamento chimico dipende dal valore di H₀ e si misura in hertz. Esso può anche essere determinato come grandezza adimensionale, δ_i = 10⁶(ν_i − ν_rif)/ν_rif, dove con δ_i indichiamo il chemical shift del nucleo in esame, con ν_i la sua frequenza di risonanza e con ν_rif quella relativa ai nuclei presi come riferimento. In questo modo lo spostamento chimico è espresso in parti per milione (ppm). Come nuclei di riferimento sono stati convenzionalmente scelti i protoni del tetrametilsilano (TMS) (CH₃)₄ Si per la scala dell'idrogeno, il ¹³C della stessa sostanza per la scala del carbonio e il ³¹P dell'H₃PO₄ a una determinata concentrazione per la scala del fosforo.

Riportiamo i valori di δ in diversi gruppi chimici dei nuclei dell'¹H (v. fig. 4), del ¹³C (v. fig. 5) e del ³¹P (v. fig. 6).

Accoppiamento spin-spin. - Sottoponiamo la molecola dell'acido fluoridrico, HF, in cui entrambi i nuclei hanno spin I = 1/2, all'azione di un campo magnetico H₀. Sia il momento magnetico del fluoro sia quello dell'idrogeno possono orientarsi parallelamente o antiparallelamente alla direzione di H₀. Avremo così le seguenti possibilità:

La presenza del momento magnetico del fluoro si traduce in un contributo positivo o negativo alla frequenza di risonanza del protone, a seconda del suo orientamento. Come conseguenza lo spettro di risonanza dell'idrogeno risulta separato in due diverse bande (v. fig. 7). La separazione tra le due bande di risonanza, misurata in hertz, è chiamata ‛costante di accoppiamento spin-spin', J; essa costituisce una misura dell'interazione tra i due nuclei e non dipende dal valore del campo magnetico impiegato.

Il valore delle costanti di accoppiamento tra due nuclei dipende, tra l'altro, dal numero e dal tipo di legami chimici che li separano e dalle loro reciproche disposizioni spaziali.

In generale, per un nucleo che possiede spin I = 1/2, nei casi più semplici - spettri di primo ordine - l'accoppiamento con n nuclei magneticamente equivalenti presenti nella molecola scinde il suo segnale di risonanza in n + 1 segnali (multipletto). Le intensità relative dei segnali sono date dai coefficienti di una espansione binomiale del tipo (x + y)ⁿ.

In base alla teoria del chemical shift, lo spettro dell'etanolo dovrebbe risultare costituito da tre bande con diverse frequenze di risonanza, le cui intensità relative (o, meglio, le cui aree) sono nei rapporti 1 : 2 : 3 e corrispondono alle concentrazioni protoniche dei gruppi OH, CH₂, CH₃. In effetti lo spettro ad alta risoluzione di questa sostanza mostra che in ognuna delle bande è presente una molteplicità di segnali (struttura fine; v. fig. 8): le bande associate al protone dell'OH (δ = 5 ppm) e ai protoni del CH₃ (δ = 1,2 ppm) sono costituite da tre segnali ciascuna, con intensità relative 1 : 2 : 1; la banda associata ai protoni del CH₂ (δ = 3,7 ppm) è costituita da un insieme di segnali di diversa intensità. Considerando i diversi protoni presenti nella molecola come dipoli magnetici, si può prevedere che la loro interazione dipenda dall'orientamento relativo e dalla distanza reciproca. Sono possibili i seguenti orientamenti dei momenti magnetici dei tre H del gruppo CH₃:

Per i due H del gruppo CH₂ si ha invece:

Per l'H del gruppo OH:

Di conseguenza i protoni del CH₃ presentano tre righe di risonanza dovute all'accoppiamento con i protoni del CH₂, con intensità 1 : 2 : 1, mentre non si ha accoppiamento con il protone dell'OH a causa dell'elevata distanza in termini di numero di legami. La probabilità che i due protoni del CH₂ si trovino orientati ↑↓ è doppia rispetto alla probabilità dei due orientamenti ↑↑ o ↓↓: da ciò deriva il rapporto 1 : 2 : 1 tra le intensità dei segnali dei protoni del CH₃, che ‛vedono' le diverse situazioni. Il protone dell'OH dà un tripletto con intensità 1 : 2 : 1 per l'accoppiamento con i protoni del CH₂, ma non è influenzato dai protoni del CH₃. Il CH₂ dà un quadrupletto per l'influenza dei protoni del CH₃, con ognuna delle quattro bande ulteriormente divisa in un doppietto per effetto del protone OH: in definitiva per il CH₂ si ha un totale di otto righe di risonanza che possono anche risultare sovrapposte in dipendenza dal valore della costante di accoppiamento con i protoni dell'OH e del CH₃.

Va rilevato che l'accoppiamento spin-spin è possibile anche tra nuclei diversi. Così lo spettro protonico dell'acido fluoridrico, HF, mostra un doppietto dovuto all'accoppiamento del protone con il fluoro e lo spettro del fluoro mostra un doppietto dovuto all'accoppiamento con il protone (v. fig. 9).

Un altro esempio è dato dall'adenosintrifosfato (ATP). Gli spettri RMN del ³¹P mostrano tre diversi segnali di risonanza (v. fig. 10) con una molteplicità di righe derivante dagli accoppiamenti spin-spin. Dall'esame dello spettro è quindi possibile l'identificazione dei segnali relativi ai tre diversi atomi di fosforo presenti nella molecola. Gli spettri dell'idrogeno e del carbonio (v. figg. 11 e 12) dell'ATP mostrano le potenzialità dell'RMN per l'identificazione, e quindi lo studio, di tutti gli atomi presenti nella molecola.

Va notato che nello spettro ¹³C (v. flg. 12) non compare la molteplicità di righe che dovrebbe derivare per l'accoppiamento di ogni nucleo ¹³C con i protoni. In questo spettro gli accoppiamenti sono stati eliminati mediante irradiazione del campione con un ulteriore campo magnetico a radiofrequenza, H₁. Tale tecnica prende il nome di ‛disaccoppiamento spin-spin'.

Consideriamo di nuovo la molecola dell'acido fluoridrico e gli orientamenti relativi possibili dei momenti magnetici nucleari. Se facciamo avvenire delle transizioni a carico dei nuclei del fluoro con un ulteriore campo magnetico a radiofrequenza, H₁, i nuclei di idrogeno non risentono più dei diversi orientamenti nel tempo dei momenti magnetici del fluoro. Di conseguenza lo spettro dell'idrogeno risulta costituito da una singola riga di risonanza, come se il fluoro non fosse presente, cioè l'idrogeno è ‛disaccoppiato' dal fluoro. Questa tecnica può essere utilizzata per eliminare accoppiamenti sia tra nuclei della stessa specie sia tra nuclei di specie diverse.

Poiché l'accoppiamento presuppone che un nucleo possa risentire, per un tempo sufficientemente lungo, degli stati energeticamente differenti di spins nucleari, il disaccoppiamento può essere ottenuto, oltre che mediante irradiazione con altri campi magnetici, anche mediante processi chimico-fisici che influenzino tale tempo. Questo è il caso, ad esempio, dei protoni mobili - idrossilici, carbossilici, amminici, ammidici - nei quali l'eventuale accoppiamento con altri nuclei può essere eliminato mediante processi di scambio con altre specie nucleari, come ²H, o scambi rapidi con la stessa specie isotopica.

Tempi di rilassamento. - Come si è visto, l'applicazione di un impulso a radiofrequenza, H₁, provoca: 1) le transizioni dei momenti magnetici tra i livelli energetici, con conseguente diminuzione della componente longitudinale, M_z, della magnetizzazione; 2) l'insorgere della magnetizzazione trasversale, M_xy. Dopo la rimozione del campo H₁ le componenti della magnetizzazione tendono a tornare al valore di equilibrio iniziale mediante due distinti processi di rilassamento: spin-reticolo e spin-spin.

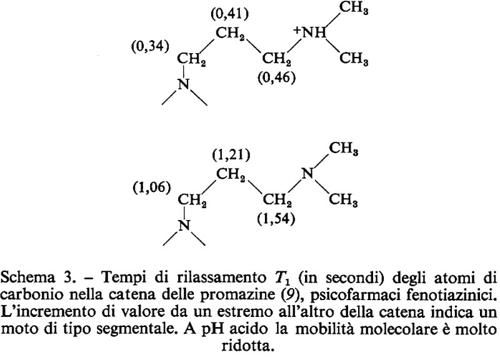
Riportando in grafico M_z in funzione di t si ricava il valore di T₁. La misura dell'efficienza del meccanismo di rilassamento è data dal valore del tempo di rilassamento spin-reticolo, T₁. Maggiore è l'efficienza del rilassamento, minore è il valore di T₁. Ad esempio, per i grassi T₁ è dell'ordine di grandezza delle centinaia di millisecondi, mentre per i protoni dell'acqua liquida è di circa 3 secondi. Questo parametro - come pure il tempo di rilassamento spin-spin, T₂ - è quindi correlabile con la dinamica molecolare a livello dei singoli atomi in una molecola.

Il metodo più usato per la misura di T₁ consiste nell'applicazione di due impulsi del campo H₁ separati da un intervallo di tempo t₀. Il primo impulso agisce per un tempo corrispondente alla rotazione di 180° della magnetizzazione; il secondo ha una durata corrispondente a una rotazione di 90°. La sequenza viene perciò indicata con 180°, t₀, 90°. Nella fig. 13 è riportata la determinazione mediante una sequenza 180°, t₀, 90° del T₁ dell'acqua in una soluzione 10^-3 M di cloruro di manganese.

Mentre il rilassamento spin-reticolo è responsabile del bilancio energetico del sistema nucleare, il meccanismo di rilassamento spin-spin non comporta alcuna cessione di energia dai nuclei al reticolo e descrive il ritorno al valore di equilibrio (nullo) delle componenti trasversali della magnetizzazione dopo la cessazione dell'impulso. Un'interazione spin-spin comporta, infatti, lo scambio dello spin tra un nucleo nello stato eccitato e uno nello stato fondamentale: il bilancio energetico di questo processo è nullo, ma lo scambio di spin contribuisce alla perdita di fase degli spins nucleari, con consegnente diminuzione della componente trasversale della magnetizzazione. Anche nel caso del rilassamento spin-spin a una maggiore efficienza del processo corrisponde un valore minore del tempo di rilassamento T₂. Tutti i meccanismi di rilassamento spin-reticolo influenzano la perdita della magnetizzazione trasversale, ma il rilassamento spin-spin non contribuisce al bilancio energetico del sistema: ne consegue che T₁ è sempre maggiore o ugnale a T₂.

Per quanto riguarda il tempo di rilassamento T₂, occorre considerare che in un campo perfettamente omogeneo, supponendo per ipotesi che non esista interazione spin-spin e che T₁ sia molto lungo - al limite infinito -, la componente trasversale della magnetizzazione non dovrebbe variare dopo l'impulso. Ma se il campo magnetico non è omogeneo, la componente trasversale diminuisce nel tempo a causa della diversa frequenza di precessione attorno a z. Questo comporta che, in generale, la variazione di M_y dopo l'impulso dipende sia dal rilassamento spin-spin sia dall'inomogeneità del campo magnetico. La costante di tempo effettiva del processo di rilassamento trasversale, T₂*, è quindi data da:

1/T₂* = 1/T₂ + (γΔH₀/2).

Un metodo di misura di T₂ deve quindi poter separare il contributo dovuto all'inomogeneità del campo da quello dovuto al rilassamento dei nuclei, eccetto nei casi in cui sia T₂ ≪ 2/γΔH₀. Il metodo usato a questo proposito è la cosiddetta sequenza spin-eco (v. risonanza magnetica nucleare: Principi fisici, suppl.).

3. Spettrometri per RMN.

Una classificazione generale degli spettrometri RMN in base alle loro caratteristiche tecniche e alle loro potenzialità di applicazione può essere fatta dividendoli in spettrometri ad alta e a bassa risoluzione. I primi sono utili per misure di spostamenti chimici, costanti di accoppiamento, tempi di rilassamento in campioni di piccole dimensioni (1-2 cm³ di volume). L'omogeneità del campo magnetico di tali spettrometri - espressa come ΔH₀/H₀ è dell'ordine di grandezza di 10^-9. Il campo magnetico può essere ottenuto con magneti permanenti o elettromagneti, fino a un valore di circa 2,5 tesla. Recentemente sono entrati in commercio magneti ‛superconduttori', ottenuti mediante passaggio di corrente in bobine di materiali particolari, raffreddate alla temperatura dell'elio liquido, che permettono di ottenere valori di campo magnetico molto elevati (oltre i 10 tesla), con l'omogeneità desiderata. Questi magneti, essendo dotati di grande sensibilità e di elevato potere risolutivo, poiché entrambe le caratteristiche dipendono dal valore di H₀, consentono di analizzare concentrazioni nucleari molto basse: per il protone fino a 10^-5 M e per il ³¹P fino a 10^-3 M.

Negli spettrometri ad alta risoluzione il campione, inserito in tubi di vetro calibrati di diametro che varia generalmente da 5 a 10 mm, viene fatto ruotare in modo da ottenere una maggiore omogeneità del campo magnetico in tutti i suoi punti. Nella fig. 14 è riportato uno schema a blocchi di uno spettrometro RMN a impulsi. Con gli spettrometri RMN ad alta risoluzione, oltre ai normali campioni è possibile analizzare anche tessuti, organi, linee cellulari, nonché diversi componenti isolati: proteine, zuccheri, fosfolipidi, ecc.

Gli spettrometri RMN a bassa risoluzione utilizzano campi magnetici di minore intensità e quindi una frequenza di irraggiamento minore e una minore omogeneità del campo magnetico H₀. Sono utilizzati per la determinazione della concentrazione delle specie nucleari e per misure dei tempi di rilassamento. In questa classe rientrano anche gli spettrometri RMN per l'ottenimento di immagini.

L'avanzamento tecnologico degli ultimi anni ha permesso di realizzare apparecchi RMN per l'ottenimento sia di spettri che di immagini da animali e anche dall'uomo (v. tomografia a risonanza magnetica nucleare, suppl.). Tali apparecchi utilizzano magneti con un'apertura da 15 a 80 cm, operanti a valori di campo magnetico di 0,15 tesla (elettromagneti) o fino a valori di circa 5 tesla (magneti superconduttori). Gli strumenti utilizzati per ottenere immagini del corpo umano di valore diagnostico operano a valori di campo magnetico variabili fino a 2 tesla.

Utilizzando gradienti di campo magnetico si ottiene la risoluzione spaziale delle risonanze della stessa specie nucleare. In base allo stesso principio dell'utilizzazione dei gradienti, ma delimitando una zona ristretta ad alta omogeneità di campo magnetico (ΔH₀/H₀ = 10^-9), si possono ottenere i corrispondenti spettri, che come risoluzione sono paragonabili a quelli ottenuti con i normali spettrometri ad alta risoluzione per campioni in vitro.

4. Composti organici.

Nel caso di sostanze organiche i nuclei di più largo impiego sono il protone e il ¹³C, ma anche le risonanze di ³¹P, ¹⁹F, ¹⁴N, ¹⁵N e di altri nuclei possono fornire informazioni complementari di grande importanza. Il protone presenta i vantaggi della maggiore sensibilità (si possono esaminare soluzioni fino a una concentrazione 10^-5 M), dell'elevata abbondanza naturale e della struttura fine delle bande di risonanza dovute all'accoppiamento spin-spin. Un aspetto negativo è rappresentato dallo stretto intervallo di spostamento chimico (circa 30 ppm), che può comportare sovrapposizione delle bande di risonanza dei nuclei che presentano piccole differenze di frequenza di risonanza. Questa difficoltà è minore nel caso di spettri ¹³C (intervallo spettrale di circa 300 ppm), il che comporta una migliore separazione dei segnali relativi ai diversi gruppi funzionali. Si hanno invece svantaggi dovuti alla bassa abbondanza naturale del ¹³C (1,1%), al valore del momento magnetico del ¹³C e, nei casi più generali, alla perdita di informazioni dovuta ad accoppiamenti spin-spin tra nuclei ¹³C. La molteplicità spettrale dovuta ad accoppiamenti con i protoni è assente quando gli spettri sono ricavati in condizioni di totale disaccoppiamento con l'¹H; tuttavia può essere ottenuta con esperimenti particolari quali la off-resonance, il gated decoupling e altri. Ulteriori vantaggi offerti dagli spettri ¹³C sono rappresentati dalla possibilità di ottenere informazioni direttamente dallo scheletro molecolare e non dalla periferia della molecola, come nel caso del protone, e dalla possibilità di investigare gruppi che non contengono atomi di idrogeno, come carbonili, isocianati, nitrili. Infine i contributi alle costanti di schermo, che sono governati da effetti elettronici intere intramolecolari, possono essere correlati direttamente con lo stato di ibridizzazione del nucleo osservato, con gli effetti induttivi, con gli effetti sterici e di van der Waals tra nuclei vicini, con l'iperconiugazione, con le interazioni mesomeriche in sistemi con elettroni a schermaggi diamagnetici con atomi pesanti, con effetti di anisotropia, con effetti isotopici.

Per confronto con dati relativi ad altri composti (v., ad es., le figg. 4, 5 e 6) si possono determinare i diversi gruppi funzionali presenti nella molecola. Inoltre è possibile calcolare, sulla base di metodi empirici, anche se in maniera approssimata, le frequenze di risonanza in dipendenza dalla natura e dalla distanza degli altri gruppi funzionali presenti nella molecola. Le eventuali variazioni della posizione dei segnali nello spettro possono essere correlate con effetti conformazionali, con fenomeni di associazione intra- e intermolecolare, ecc. Tali variazioni possono, tra l'altro, dipendere da: a) effetti di legami e di residui anisotropi; b) non equivalenza magnetica.

Effetti di legami e di residui anirotropi. - Numerose correlazioni tra lo spostamento chimico e aspetti stereochimici sono basate su interazioni con sostituenti presenti nella molecola a lunga distanza dal nucleo considerato. Ad esempio, la presenza di centri magneticamente anisotropi, come carbonili, anelli aromatici e insaturazioni, ma anche di legami tra eteroatomi o atomi non equivalenti, comporta lo spostamento delle risonanze protoniche in dipendenza dalla conformazione molecolare. Effetti di questo tipo hanno contribuito a determinazioni strutturali, come nella serie dei diterpeni, dei ciclobutani, delle nitrosammine eterocicliche. Tali effetti sono anche funzione delle condizioni chimico-fisiche del campione: così nel caso di omopolipeptidi e di eteropolipeptidi, gli effetti ottenuti con variazioni delle condizioni chimico-fisiche (pH, temperatura, solventi) hanno dato importanti contributi nella determinazione strutturale, ma anche nello studio degli equilibri tra le conformazioni possibili. Per quanto riguarda tali effetti, in alcuni casi - come doppi legami, legami peptidici, fenili, annuleni e loro derivati, bifenilene e in generale sistemi aromatici policiclici - sono stati anche sviluppati modelli di calcolo in discreto accordo con i dati sperimentali. Infine interessanti sono le informazioni di tipo strutturale ricavabili mediante effetti intermolecolari dello stesso tipo, come nel caso di sostanze disciolte in solventi aromatici.

Non equivalenza magnetica. - La presenza di un centro di asimmetria in una molecola comporta in linea di principio le condizioni per cui, ad esempio, i protoni metilenici di un gruppo etilico o i protoni metilici di un gruppo isopropilico sono potenzialmente non equivalenti. Un esempio di questo fenomeno è il dietilacetale dell'aldeide acetica, CH₃CH₂OCH(CH₃)OCH₂CH₃, dove i protoni metilenici presentano diversi spostamenti chimici e diverse costanti di accoppiamento ¹H-¹³C. Analoghi risultati si sono avuti in vari sali di solfonio, esteri ed eteri etilici asimmetrici. La non equivalenza magnetica e le variazioni conseguenti di spostamento chimico di alcuni gruppi possono essere esaltate dalla maggiore probabilità sterica di alcune conformazioni. È questo il caso della N-nitroso-N-benzilcloroanilina, in cui per la forma cis i protoni metilenici sono non equivalenti.

Un caso particolare di non equivalenza magnetica si ha quando una miscela racemica è disciolta in un solvente otticamente attivo. L'interazione solvente-soluto può essere diversa per gli enantiomeri e mostrare una diversità della frequenza di risonanza dei nuclei nelle due forme corrispondenti.

L'entità dell'interazione di spin, di cui la costante di accoppiamento J è una misura, dipende dal numero di legami che separano i nuclei interagenti. Poiché tale interazione si trasmette per lo più tramite gli elettroni di legame, fattori che mutano la distribuzione elettronica dei legami attraverso i quali i nuclei si accoppiano - quali molteplicità dei legami, elettronegatività dei sostituenti e polarizzazione di legami - provocano la variazione delle costanti di accoppiamento. Le J tra protoni geminali attraverso un atomo di carbonio ibridizzato sp³ sono dell'ordine di 0 ÷ 25 Hz e negative, con alcune eccezioni come negli epossidi. Per un sistema tipo

J è dell'ordine di 12 ÷ 15 Hz e negativa. In generale J dipende: a) dall'elettronegatività del sostituente; b) dall'angolo tra i protoni; c) dall'eventuale numero di legami π adiacenti. Le costanti di accoppiamento geminali attraverso un atomo di carbonio ibridizzato sp² sono minori e variano da − 2 a + 3 Hz. Con un eteroatomo legato a H₂C=, come nella formaldeide, la J_gem è pari a 42 Hz ed è la più alta in assoluto dopo la J_H-H nella molecola di H₂ (J = 285 Hz). Nei sistemi saturi la J_vic (l'indice ‛vic' sta per ‛vicinale') varia da 0 a 16 Hz ed è positiva. Quando esiste libera rotazione intorno al legame C-C la J_vic osservata è una media dei singoli conformeri, la cui probabilità relativa può essere ricavata dalla dipendenza dall'angolo diedro, θ, data approssimativamente dalle equazioni di Karplus

con J₀ e J₁₈₀ valori delle costanti di accoppiamento nella conformazione cis e trans, rispettivamente. Si è riscontrato un buon accordo qualitativo fra le equazioni di Karplus e i risultati sperimentali. Così, nel caso di strutture tipo cicloesano, è stato possibile stabilire le differenti orientazioni di atomi di idrogeno vicinali, cioè diequatoriale, diassiale, assiale-equatoriale:

Altri fattori che influenzano la J_vic sono l'elettronegatività del sostituente e lo stato di ibridizzazione degli atomi di carbonio. Ad esempio negli alcheni la J_HC-CH è compresa tra 5 e 8 Hz, nei dieni trans tra 10 e 12 Hz. Essendo inoltre le J_trans costantemente maggiori delle J_cis - rispettivamente 0 ÷ 12 Hz e 12 ÷ 20 Hz - vi è la possibilità di assegnazione della configurazione anche avendo a disposizione un solo isomero. Per le olefine cicliche la J_cis diminuisce in dipendenza dalla diminuzione delle dimensioni dell'anello. Nei sistemi aromatici ed eteroaromatici si ha J_orto > J_meta > J_para, con una diminuzione nei rispettivi valori al diminuire delle dimensioni dell'anello (piridina J_2,3 = 5 Hz; pirrolo J_2,3 = 5 Hz; chinolina J_2,3 = 4 Hz; indolo J_2,3 = 3 Hz).

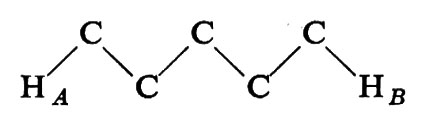
Altre utili informazioni strutturali possono essere derivate da accoppiamenti a lunga distanza, cioè tra protoni separati da tre o più legami. È questo il caso di sistemi tipo allilico o omoallilico. Le costanti di accoppiamento alliliche sono di segno negativo e comprese tra 0 e 3 Hz; la J_{1,2 cisoide} ha circa lo stesso valore della J_{1,2 transoide}; queste costanti di accoppiamento dipendono dall'angolo allilico, ossia sono proporzionali al grado di sovrapposizione degli orbitali s, p: se l'angolo allilico ha valore 0° o 180° hanno valore zero, mentre se è pari a 90° hanno il massimo valore negativo. Le costanti di accoppiamento omoalliliche sono di segno positivo e comprese tra 0 e 4 Hz.

Accoppiamenti si hanno anche tra protoni separati da 4 legami semplici in sistemi tipo

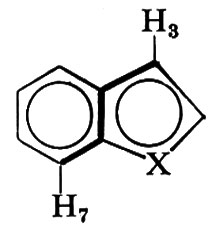
specie in strutture cicliche. Esempi di costanti di accoppiamento stericamente dipendenti tra protoni separati da 5 o più legami si hanno nelle serie degli alcheni e degli annuleni, come pure in sistemi saturi e con insaturazioni coniugate. Così gli idrogeni in posizione 3 e 7 in composti tipo

o gli idrogeni in posizione 4 e 8 in composti tipo

mostrano J positive comprese tra 0,4 e 2 Hz.

Anche le costanti di accoppiamento tra eteroatomi hanno dato informazioni sulle strutture molecolari. Nel caso di accoppiamento ¹H-¹³C attraverso un solo legame, oltre a una dipendenza dall'elettronegatività di eventuali sostituenti, si è ricavata una relazione empirica tipo: ¹J_C-H = 5x (% carattere s dell'atomo ¹³C) Hz. In generale, inoltre, si ha una dipendenza dalla stereochimica per le costanti di accoppiamento tra ¹³C e protoni sullo stesso atomo e sui due atomi di carbonio primi vicini.

Per quanto riguarda l'accoppiamento ¹H-¹⁹F, oltre che dall'angolo diedro, è stato mostrato che esso è dipendente dalla lunghezza del legame e dall'angolo F−C−C, variando tra 0,9 e 31 Hz per angoli di circa 118° e 109° rispettivamente, con angolo diedro di 0°. Anche per ¹H-¹⁹F l'accoppiamento a lunga distanza può variare di segno: così, nel caso del 7,7′-difluoro-biciclo(2,2,1)eptene, varia da 1,12 a −5,44 Hz.

Una dipendenza dalla stereochimica si ha anche nel caso degli accoppiamenti ¹H-³¹P. Così si hanno valori variabili da 26 a −6 Hz, in funzione dell'angolo diedro tra i due piani definiti da P−C−H e dal legame P−C. Un analogo comportamento si ha per gruppi P−O−C−H, presenti ad esempio in esteri fosfati ciclici, fosfiti ciclici, diossafosforinani. Anche accoppiamenti ¹H-³¹P a lunga distanza hanno mostrato dipendenze stereochimiche.

Pure i tempi di rilassamento sono stati utilizzati per ottenere informazioni strutturali in molecole organiche. Per i carboidrati, ad esempio, è stata messa in evidenza una dipendenza dei T₁ protonici dalla configurazione. In derivati del glucosio il protone anomerico mostra valori più brevi di T₁, dell'ordine di 1 ÷ 2 s, quando è in posizione assiale e notevolmente più lunghi (4 ÷ 5 s) quando è in posizione equatoriale, consentendo quindi la determinazione delle eventuali forme presenti.

Nel caso degli oligosaccaridi si sono ottenuti interessanti risultati prendendo in esame i tempi di rilassamento del ¹³C. Così nello stachiosio il valore di T₁ dei diversi atomi di ¹³C ha reso possibile evidenziare la diversa mobilità dei due anelli galattosici.

Per quanto riguarda i rilassamenti del ¹³C esiste una proporzionalità tra l'inverso del valore di T₁ dell'atomo ¹³C e il numero di protoni a esso legati. In tal modo si possono differenziare immediatamente i diversi tipi di carbonio: primario, secondario, terziario e quaternario. Per quel che riguarda studi di isomeri, nel caso di composti aromatici, come benzeni monosostituiti, i ¹³C in posizione para rispetto al sostituente rilassano più velocemente di quelli in meta e orto. Per aromatici disostituiti, come gli xileni, l'isomero para esibisce valori di T₁ più corti dei corrispondenti isomeri orto e meta.

5. Composti paramagnetici.

La presenza di un centro paramagnetico influenza lo spettro RMN dei nuclei di una molecola attraverso l'interazione tra gli elettroni non accoppiati del centro paramagnetico e i nuclei stessi. Tali interazioni comportano per i diversi nuclei spostamenti iperfini isotropici, variazioni dei tempi di rilassamento spin-spin e spin-reticolo e polarizzazione degli spins nucleari.

Dallo studio di tali effetti possono essere ricavate informazioni sulla distribuzione elettronica in complessi metallici, sulla loro struttura, sulla formazione di coppie di ioni in soluzione, su fenomeni di solvatazione, ecc. Informazioni di questo tipo sono state ottenute su complessi tra ioni paramagnetici e composti di basso peso molecolare e anche macromolecole biologiche. Un campo di applicazione estremamente interessante è costituito dall'uso di complessi paramagnetici come mezzi di contrasto nelle immagini RMN (v. tomogragia a risonanza magnetica nucleare, suppl.).

La frequenza di risonanza di un nucleo in un composto contenente un centro paramagnetico è spostata rispetto a un ipotetico analogo composto diamagnetico. Questo spostamento dipende dall'interazione con gli elettroni spaiati ed è riconducibile a due diversi meccanismi: 1) spostamento di contatto, dovuto alla delocalizzazione della densità degli spins elettronici spaiati sul nucleo che risuona (l'effetto usualmente si trasmette attraverso i legami chimici); 2) spostamento di pseudocontatto o spostamento dipolare, risultante dall'interazione dipolare tra gli spins elettronici e gli spins nucleari (è il solo contributo osservato quando il campo prodotto dagli elettroni spaiati è anisotropo).

La presenza di un centro paramagnetico comporta anche la variazione dei tempi di rilassamento. Per entrambi i tempi di rilassamento, T₁ e T₂, il contributo dominante è dovuto all'interazione dipolare, che è funzione della distanza tra il centro paramagnetico e il nucleo. Di conseguenza si possono avere informazioni sulla struttura e sulla dinamica molecolare.

Tramite le variazioni di spostamento chimico e dei tempi di rilassamento è possibile: a) determinare la struttura, la cinetica e il meccanismo di formazione di complessi organometallici; b) investigare il ruolo funzionale degli ioni metallici in sistemi biologici; c) studiare l'aumento della velocità di rilassamento dei protoni dell'acqua in presenza di specie paramagnetiche; d) utilizzare i metalli paramagnetici per determinazioni diagnostiche. Si deve ricordare infatti che l'intensità del segnale RMN a immagini dipende dalla densità protonica e dai tempi di rilassamento. Mediante l'uso di particolari sequenze di impulsi e mediante la variazione dei fattori temporali che le caratterizzano è possibile modulare l'influenza dei parametri spettroscopici sulla formazione dell'immagine. In altri termini, i cambiamenti indotti nei parametri RMN tramite la modificazione del contributo dovuto alla densità protonica o ai tempi di rilassamento del campione possono migliorare il contrasto e la qualità dell'immagine (v. tomografia a risonanza magnetica nucleare, suppl.).

6. Polimeri sintetici.

Una macromolecola lineare si può considerare come una successione di unità monomeriche nella quale sono contenuti tre tipi di informazioni: l'informazione chimica, l'informazione configurazionale, l'informazione conformazionale.

L'informazione chimica è relativa alla natura delle unità monomeriche che si succedono nella catena. Se tali unità monomeriche sono uguali, come nel caso di un omopolimero, l'informazione chimica è nulla.

L'informazione configurazionale è relativa alla disposizione spaziale degli atomi che caratterizzano un dato stereoisomero. Se l'unità monomerica è simmetrica, l'informazione configurazionale è nulla.

L'informazione conformazionale è relativa alle diverse disposizioni spaziali degli atomi che possono trasformarsi le une nelle altre senza rottura di legami. Una macromolecola priva di informazioni chimiche e configurazionali, in cui vi sia una successione identica o alternante di stati conformazionali diversi delle unità monomeriche, ha una informazione conformazionale nulla.

Consideriamo una catena - come un polipeptide - del tipo

Essa può essere immaginata come una ripetizione di legami A−B, B−C, C−A. Conseguentemente a quanto si è detto, tutte le possibili conformazioni della catena possono essere descritte in funzione degli angoli di rotazione attorno ad A−B (ϕ), B−C (ψ), C−A (ω). Imponendo il principio di equivalenza conformazionale, si ha che gli angoli di torsione relativi a triplette successive devono essere identici. È ovvio che nel caso di

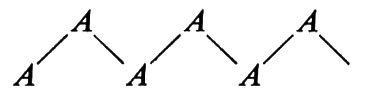
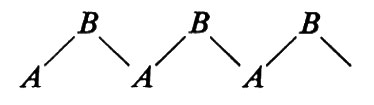
si ha solo un angolo di torsione che deve soddisfare questa condizione, mentre nel caso di

si hanno due angoli di torsione: attorno ad A−B e a B−A, rispettivamente.

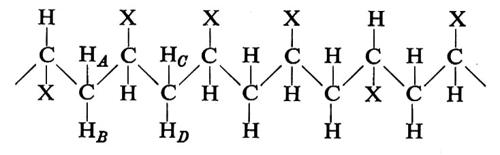
Le principali caratteristiche di uno spettro RMN ad alta risoluzione possono essere usate per ottenere informazioni riguardanti l'analisi qualitativa e quantitativa dei diversi residui contenuti, la sequenza in termini di monomeri e la stereochimica della catena macromolecolare. Nel caso di polimeri ottenuti da monomeri vinilici, fino a qualche anno fa la maggior parte dei risultati è stata ottenuta esaminando le risonanze dei protoni e del fluoro. Tuttavia non è sempre possibile interpretare compiutamente gli spettri ricavati, soprattutto nel caso dei protoni, e in generale si può dire che uno spettro RMN protonico di un polimero contiene un maggior numero di informazioni di quante è possibile comprenderne, stanti le conoscenze teoriche attuali. Un miglioramento sostanziale si è avuto mediante l'impiego di spettrometri operanti a valori maggiori di campi magnetici, che hanno permesso una migliore risoluzione degli spettri.

Negli ultimi anni la possibilità di ottenere spettri RMN del ¹³C in abbondanza naturale e spettri di campioni allo stato solido mediante spettrometri a impulsi ha aperto nuove prospettive.

La sequenza configurazionale che si determina in una catena polimerica può essere descritta in generale secondo un processo bernoulliano o markoviano.

Semplificando si può dire che nella descrizione bernoulliana l'attacco di una unità monomerica a una catena in crescita è completamente indipendente dalla stereochimica dei terminali di quest'ultima. Al contrario, nella descrizione markoviana la stereochimica del terminale (ordine zero) della penultima unità monomerica della catena in crescita (primo ordine) influenza direttamente quella dell'unità monomerica che accresce la molecola. In corrispondenza di questi processi si possono calcolare le relative probabilità in termini di sequenze. La loro distribuzione, evidentemente di notevole interesse sia teorico che pratico, non ha avuto dimostrazione sperimentale eccetto che nel caso di alcuni polimeri ben cristallizzabili, vale a dire altamente stereospecifici, per i quali è stata possibile l'analisi anche mediante la tecnica della diffrazione dei raggi X. In tutti gli altri casi l'applicazione di varie tecniche, come le proprietà di solubilità, il punto di fusione, la spettroscopia a raggi infrarossi e la reattività chimica, ha fornito al massimo informazioni qualitative.

L'applicazione dell'RMN permette sia di verificare le predizioni teoriche, sia di correlare la stereoregolarità con altre proprietà fisiche.

Lo spostamento chimico di un protone, come detto in precedenza, può essere espresso come la somma dei contributi dovuti ai gruppi direttamente o indirettamente legati al nucleo in esame. Consideriamo un polimero vinilico come una catena di atomi di carbonio che giacciono sul piano normale al piano del disegno:

Se si considerano i gruppi sostituenti legati agli atomi di carbonio primi vicini, H_A e H_B sono magneticamente equivalenti, mentre i protoni H_C e H_D sono magneticamente non equivalenti. Inoltre, se si considerano le unità monomeriche prime vicine, il protone legato al C₅ è in posizione isotattica, quello legato al C₇ è in posizione eterotattica. Queste non equivalenze steriche, cui corrispondono non equivalenze magnetiche, danno luogo a risonanze diverse nello spettro protonico. Basandosi sull'additività dei vari contributi allo spostamento chimico di un nucleo, l'RMN è capace di distinguere tra le diverse sequenze conformazionali, e tale analisi è tanto più accurata quanto maggiore è la risoluzione spettrale. A questo proposito va rilevato che, oltre all'ovvia dipendenza della risoluzione dal valore del campo magnetico, irradiando selettivamente i diversi protoni (doppia e tripla risonanza), si possono eliminare le interazioni spin-spin con la conseguente semplificazione dei segnali di risonanza. Un analogo risultato si può ottenere mediante la deuterazione selettiva dei diversi residui protonici, con conseguente scomparsa dei segnali a essi corrispondenti e degli accoppiamenti spin-spin relativi. Con questi accorgimenti si possono ricavare le costanti di accoppiamento relative ai vari residui e ottenere informazioni conformazionali.

Risultati analoghi e complementari si possono ottenere con spettri RMN del ¹³C. Così nel caso del polipropilene, del polimetilmetacrilato e in altri, nei quali è stata possibile l'analisi in termini di sequenze isotattiche, sindiotattiche, eterotattiche.

Infine, la misura dei tempi di rilassamento delle diverse risonanze può dare informazioni sulla dinamica molecolare dei vari residui all'interno della macromolecola.

Interessanti le applicazioni dell'RMN ai copolimeri sintetici. La teoria della copolimerizzazione di monomeri vinilici è stata sviluppata già da molti anni ed è stata confermata da diversi studi.

La quasi totalità di questi consiste tuttavia di determinazioni analitiche di rapporti di monomeri nei copolimeri, in funzione del rapporto di monomeri nella miscela di reazione, con pochissime informazioni sulla lunghezza delle sequenze e nessuna riguardante la configurazione della catena del copolimero. La stessa equazione che predice la composizione del copolimero predice anche la lunghezza delle varie sequenze, ma non ha mai avuto conferma sperimentale.

A questi problemi l'RMN può fornire una risposta diretta. Tralasciando il problema analitico della determinazione delle percentuali relative di comonomeri, che è di facile e intuibile risoluzione, e non considerando la stereochimica delle unità monomeriche, avremo diversi tipi di sequenze:

L'analisi degli spettri RMN protonici ha permesso di determinare tali sequenze in molti copolimeri, per esempio nel caso del copolimero etilene/propilene, dove si sono potute assegnare le sequenze triadiche, e del copolimero vinilacetato/etilene, in cui si è eseguita l'analisi in termini di diadi.

In questo genere di applicazioni ancor più promettente è l'uso dell'RMN del ¹³C, con cui si è determinata la sesequenza e la tatticità di copolimeri etilene/propilene e di vari butadieni.

Quanto detto vale anche per spettri ottenuti allo stato solido. In questo caso, inoltre, il confronto con gli spettri ottenuti in soluzione può mettere in evidenza le eventuali influenze dovute al solvente.

7. Alcune applicazioni chimico-fisiche.

a) Studi termodinamici.

Nel caso generale di un equilibrio tra due stati le quantità termodinamiche possono essere determinate solo quando le caratteristiche degli spettri RMN nei due stati sono diverse. In tal caso possono essere determinate costanti di equilibrio, calori ed entalpie di legame, pK, coefficienti di ripartizione di una molecola tra diversi compartimenti.

Mentre per molte di queste determinazioni l'RMN è alternativa ad altri metodi, essa è il solo metodo generale per la determinazione del valore di pK, che può essere ottenuto una volta messa in evidenza la sua influenza su una particolare banda di risonanza di una molecola. Ad esempio, per spiegare l'effetto Bohr nell'emoglobina, effetto in cui il rilascio dei protoni si osserva accoppiato alla formazione del legame con l'ossigeno, fu suggerito da M. Perutz, in base a evidenze cristallografiche, che l'istidina β-146 dovesse essere coinvolta nel fenomeno, poiché nella forma desossi dell'emoglobina, al contrario della forma ossi, l'aspartico β-94 è sufficientemente vicino all'istidina da alterarne il pK. Il comportamento della risonanza del carbonio in posizione 2 dell'istidina β-146 e la conseguente determinazione del suo pK nelle forme ossi e desossi hanno confermato l'ipotesi di Perutz.

Studi analoghi possono essere compiuti in vivo, analizzando le risonanze anche di altri nuclei come il ³¹P, il cui spostamento chimico in alcuni gruppi presenti nei metaboliti, come il fosfato inorganico e il 2,3-difosfoglicerato, dipende dal valore di pH.

b) Studi strutturali.

Sebbene molte tecniche spettroscopiche siano sensibili alla struttura tridimensionale delle molecole, è spesso impossibile correlare un cambiamento spettrale a un dettagliato cambiamento strutturale. Tale difficoltà aumenta con il peso molecolare. Rispetto ad altre tecniche, come il dicroismo circolare, la fluorescenza e la risonanza elettronica di spin, l'RMN è potenzialmente in grado di fornire un modello strutturale basato solo su dati spettroscopici: il comportamento magnetico di un nucleo dipende dalla sua geometria rispetto ai nuclei circostanti; lo spostamento chimico, le proprietà di rilassamento e le costanti di accoppiamento sono il risultato di perturbazioni specifiche dipendenti dalla struttura a livello di singolo residuo e quindi con essà correlabili. A tale riguardo la conoscenza della struttura cristallina di una proteina può essere molto utile per l'assegnazione delle diverse bande di risonanza ai diversi residui nel corrispondente spettro RMN. Tuttavia i lavori sul glucagone e sull'inibitore della tripsina pancreatica hanno mostrato che in alcuni casi favorevoli l'osservazione di interazioni tra i diversi nuclei può portare alla determinazione della struttura molecolare solo in base alla conoscenza della sua sequenza primaria.

Da notare inoltre che un'assegnazione completa delle risonanze presenti in uno spettro non è sempre strettamente necessaria. Spesso lo studio solo di alcune risonanze provvede uno strumento esauriente per la determinazione del comportamento di una macromolecola. Così nel caso dell'RNA di trasferimento l'osservazione dello spettro relativo ai soli gruppi NH impegnati in legami a idrogeno (a circa 11 ppm) ha fornito delucidazioni sul processo di denaturazione termica. Alcune macromolecole di peso molecolare elevato, che tendono a dare spettri con bande allargate e poco risolte, possono tuttavia presentare alcune risonanze ben risolte, in corrispondenza delle regioni più mobili della macromolecola. Nel caso della piruvatodeidrogenasi (peso molecolare di circa 2 × 10⁵ dalton) del Bacillus stearothermophilus è stato possibile individuare e studiare alcune delle risonanze corrispondenti ai residui della parte mobile della struttura del complesso che si forma tra l'apoenzima e il coenzima acido lipoico.

Le informazioni strutturali si correlano direttamente con la dinamica delle macromolecole e quindi con la loro eventuale attività funzionale. In generale i processi che provocano la variazione delle distanze internucleari, i moti interni delle molecole e gli scambi chimici sono anche in grado di influenzare i parametri caratteristici di uno spettro RMN.

L'osservazione, compiuta tramite RMN, della mobilità della struttura tridimensionale delle macromolecole ha portato, dopo accese discussioni, alla conclusione che la flessibilità strutturale è inerente a tutte le strutture polimeriche e, sebbene in modo diversificato per le diverse macromolecole, svolge un conseguente ruolo funzionale nell'interazione con altre molecole di importanza strutturale o metabolica.

c) Studi cinetici.

In molti casi l'effetto dei processi di scambio o delle reazioni chimiche sulle intensità, sullo spostamento chimico e sui tempi di rilassamento dei segnali RMN può essere analizzato quantitativamente per ottenere costanti di velocità ed energie di attivazione.

Per un nucleo che scambia la sua posizione nel tempo tra due siti A e B magneticamente non equivalenti (come il protone

cis o trans in un'ammide) la magnetizzazione è data da

con τ_A e τ_B tempi di vita nello stato A e B del nucleo in esame,

ν₀ frequenza di risonanza di riferimento, ν_A e ν_B frequenze di risonanza del nucleo nei siti A e B, p_A e p_B popolazioni del nucleo nello stato A e B e M₀ magnetizzazione all'equilibrio.

Tale espressione rappresenta la magnetizzazione totale in condizioni di scambio e fornisce la possibilità di calcolare le varie forme d'onda in funzione dei diversi parametri, che, confrontate con quelle sperimentali (spettri), permettono di ricavare i valori di τ. Così, per esempio, determinando i valori di τ_A e τ_B in funzione della temperatura, si può determinare l'energia di attivazione ΔE di un processo in base all'equazione

1/τ = ν₀e^-ΔE/RT,

con ν₀ fattore di frequenza.

Cambiamenti di concentrazione di una specie chimica coinvolta in una reazione si possono seguire tramite le variazioni di intensità del segnale corrispondente. La scala dei tempi effettivamente analizzabili varia da 10^-3 s fino a ore o più. In questo modo sono state studiate le variazioni nel tempo della concentrazione di metaboliti coinvolti nel processo di contrazione muscolare. Altri esempi di applicazione dell'RMN a studi cinetici riguardano: cambiamenti conformazionali del lisozima a seguito del legame con l'inibitore, studiati seguendo le variazioni dello spettro ¹H dell'intero enzima; le velocità di rotazione di un singolo residuo, come nel caso della tirosina nel citocromo c; cinetiche di scambio dei gruppi fosfato tra nucleotidi a opera dell'enzima chinasi. Inoltre, poiché i parametri RMN sono funzione dell'ambiente molecolare che circonda il nucleo in esame, è stato possibile dimostrare diverse cinetiche di reazione per i due isoenzimi dell'anidrasi carbonica. Infine, si sono analizzati sistemi di trasporto molecolare attraverso vescicole fosfolipidiche e membrane naturali. Lo studio cinetico della creatinchinasi è stato compiuto in vivo su muscoli di rana tramite la misura della velocità di scambio del fosfato in posizione γ dell'adenosintrifosfato con la creatina. Con lo stesso principio possono essere studiate le cinetiche delle adenosintrifosfatasi e dell'adenilatochinasi. In questi casi si è ottenuta per la prima volta la possibilità di studiare la cinetica di alcune reazioni catalizzate da enzimi in vivo, in tessuti e in cellule.

Per studi cinetici si possono anche introdurre opportuni nuclei ‛sonda' e registrarne gli effetti sugli spettri: se globuli rossi vengono sospesi in ²H₂O, il segnale del protone legato al carbonio in posizione 3 del lattato diminuisce progressivamente a causa della sostituzione con il deuterio. La velocità di conversione del lattato in piruvato può essere così misurata dalla velocità di scambio tra ¹H e ²H.

Anche l'uso di sostanze paramagnetiche (metalli di transizione e lantanidi) si è rivelato molto interessante grazie agli effetti della loro interazione con alcuni nuclei che riguarda sia la frequenza di risonanza dei segnali RMN sia i tempi di rilassamento. Le variazioni dei tempi di rilassamento delle risonanze ³¹P o ²³Na hanno permesso di individuare componenti intra- ed extracellulari e di studiarne le velocità di scambio attraverso le membrane. Di particolare interesse sono gli studi in vivo sul metabolismo (v. risonanza magnetica nucleare: Applicazioni biochimiche e biologiche, suppl.).

Rispetto ad altre tecniche di tipo spettroscopico o di tipo strettamente biochimico i vantaggi offerti dall'RMN riguardano fondamentalmente la possibilità di compiere analisi non distruttive del campione e non lesive delle strutture e delle funzioni degli organismi in vivo. È possibile seguire sullo stesso campione gli eventi metabolici nel tempo, osservare simultaneamente vari composti presenti, anche prendendo in esame nuclei di atomi diversi, ammesso che la loro concentrazione sia sufficientemente elevata, senza ricorrere a estrazione e purificazione dei componenti, procedure che possono avere come conseguenza la distruzione del campione o l'alterazione delle condizioni fisiologiche. Inoltre non è necessario, come in altre tecniche spettroscopiche, l'uso di composti sonda o di mezzi di contrasto con la conseguente possibilità di introdurre alterazioni nelle strutture in esame.

Data la complessità degli spettri ottenibili da cellule, tessuti, organi o, in generale, da campioni in vivo, un notevole aiuto per la loro interpretazione viene fornito dalle conoscenze derivate dall'impiego di altre tecniche, oppure da spettri RMN dei diversi componenti isolati o di frazioni ottenute per estrazione del campione con solventi.

Una proprietà estremamente interessante dell'RMN consiste nella possibilità di seguire nel tempo sullo stesso campione i diversi metaboiiti, in un organo o in un tessuto; tale caratteristica offre un metodo ideale per correlare lo stato metabolico con la funzione fisiologica. Dall'analisi dei parametri spettrali si possono ottenere, in linea di principio, tutte le informazioni che sono state viste in precedenza per molecole isolate. In effetti sono stati determinati la mobilità di alcune macromolecole, il pH intra- ed extracellulare di tessuti e organi in diverse condizioni sperimentali, la concentrazione di alcuni metaboliti e la loro compartimentazione cellulare, l'effetto dell'interazione tra metaboliti e ioni, cinetiche di reazione e di scambio tra i compartimenti cellulari.

Gli isotopi utilizzati finora per studi in vivo sono soprattutto ¹H, ¹³C, ³¹P e, ultimamente, ²³Na. Ciò per ragioni di concentrazione nei materiali biologici, di abbondanza naturale dell'isotopo e di sensibilità dei nuclei. Vale la pena di accennare che questi stessi nuclei, e soprattutto ¹H, sono utilizzati per ottenere immagini RMN dell'interno del corpo umano (v. tomografia a risonanza magnetica nucleare, suppl.).

L'isotopo ¹H ha le migliori caratteristiche di sensibilità. Esso inoltre è il più abbondante nei materiali biologici, essendo presente nell'acqua, nei grassi e nella maggior parte dei metaboliti. A causa della sua ubiquità e dello stretto intervallo in cui cadono le varie bande di risonanza (di circa 15 ppm) si osserva una notevole complessità degli spettri, con la conseguente difficoltà di interpretazione. Si possono tuttavia ottenere molte informazioni sfruttando le caratteristiche chimico-fisiche dei diversi gruppi, soprattutto di quelli che cadono in zone particolari dello spettro.

Il ³¹P, oltre a essere il solo isotopo del fosforo presente in natura, offre il vantaggio di mostrare un vasto campo di valori di spostamento chimico in dipendenza dal suo intorno e di consentire, quindi, l'individuazione di molti dei composti contenenti fosforo, biologicamente importanti. Così, ad esempio, è stato possibile seguire nel tempo il metabolismo energetico riguardante i composti fosforilati direttamente su organi in condizioni di perfusione. Dagli spettri si ottengono informazioni sulle relazioni tra stato metabolico e funzioni fisiologiche del tessuto, e anche sulle condizioni di conservazione e sopravvivenza degli organi, informazioni di estrema utilità per le applicazioni mediche. Studi di questo tipo hanno permesso l'identificazione di molecole la cui presenza era insospettata e non rilevabile con indagini biochimiche che comportano la manipolazione e possibili conseguenti modificazioni del campione.

Tra gli studi più interessanti vanno ricordati gli esperimenti ³¹P-RMN condotti su organi animali in condizioni fisiologiche, in cui si può seguire, in funzione del tempo e in funzione di sollecitazioni fisiche o chimiche, la variazione della concentrazione delle sostanze coinvolte nel metabolismò energetico. Ad esempio, il decorso metabolico di una stimolazione elettrica compiuta sul muscolo può essere seguito registrando gli spettri ³¹P-RMN a tempi diversi, prima e dopo la stimolazione. Analoghi esperimenti possono essere eseguiti utilizzando molecole farmacologicamente attive.

Nonostante che il carbonio sia il secondo elemento, per abbondanza, nei tessuti biologici, esso mal si presta a studi biochimici mediante spettroscopia RMN. Infatti il suo isotopo più abbondante è il ¹²C, che, avendo momento magnetico nullo, non dà risonanza magnetica nucleare. Questa si ottiene invece dall'isotopo ¹³C, presente in natura per l'1,1% circa. Anche a causa della sua bassa sensibilità, per ottenere spettri da questo isotopo sono necessari tempi di acquisizione lunghi. È possibile tuttavia l'arricchimento isotopico mediante opportuni substrati di reazione. In tal modo sono stati possibili studi in vivo sul metabolismo degli zuccheri. Il metabolismo del glucosio è stato studiato in vivo su batteri, seguendo nel tempo il destino di precursori metabolici, arricchiti selettivamente in ¹³C. Si può così seguire la ridistribuzione del ¹³C tra gli intermedi e i prodotti metabolici, determinando le velocità di flusso delle sostanze coinvolte, attraverso alcune sequenze di reazioni biochimiche, nonché alcune stereospecificità enzimatiche e vie biosintetiche batteriche, come quelle seguite nella biosintesi di antibiotici quali la penicillina e la cefalosporina.

Bibliografia.

Bovey, F.A., High resolution NMR of macromolecules, New York 1971.

Breitmaier, E., Haas, G., Vaelter, W., Atlas of Carbon-13 NMR data, London 1979.

Bruegel, W., Handbook of NMR spectral parameters, London 1979.

Carrington, A., Mc Lachlan, A.D., Introduction to magnetic resonance with applications to chemistry and chemical physics, New York 1967.

Conti, F., Delfini, M., Di Cocco, M.E., Parasassi, T., Introduzione alla risonanza magnetica nucleare in medicina, Roma 1982.

Emsley, I. W., Ferrey, J., Sutcliffe, L.H., High resolution nuclear magnetic resonance spectroscopy, Oxford 1965.

Farrar, T.C., Becker, E.D., Pulse and Fourier transform NMR, New York 1971.

Gadiani D.G., Nuclear magnetic resonance and its applications to living systems, Oxford 1982.

Harris, R.K., Mann, B.E., NMR and periodic table, London 1978.

La Mar, G.N., Dew Harrocks, W. jr., Holm, R.H., NMR of paramagnetic molecules, New York 1973.

Levy, G. C., Nelson, G. L., Carbon-13 nuclear magnetic resonance for organic chemists, New York 1972.

Martin, M. L., Delpuech, J. J., Martin, G. J., Practical NMR spectroscopy, London 1980.

Randall, J. C., Polymer sequence determination: Carbon-13 NMR method, New York 1978.

Shaw, D., Fourier transform NMR spectroscopy, Amsterdam 1976.

Simons, W.W., The Sadtler handbook of proton NMR spectra, Philadelphia-London 1978.

Stothers, J.B., Carbon-13 NMR spectroscopy, New York 1972.

Applicazioni biochimiche e biologiche di Rosanna Mondelli

SOMMARIO: 1. Introduzione. □ 2. La spettroscopia protonica: applicazioni all'analisi strutturale di sostanze naturali. □ 3. La spettroscopia del ¹³C e le sue applicazioni alla biosintesi di sostanze naturali. □ 4. Studio della conformazione delle biomolecole e della dinamica molecolare. □ 5. La risonanza del fosforo e gli sviluppi della spettroscopia in vivo. □ 6. Prospettive future. □ Bibliografia.

1. Introduzione.

L'enorme diffusione che l'RMN ha avuto è sicuramente legata al successo ottenuto dai chimici nella determinazione della struttura di composti organici. Questa tecnica spettroscopica, infatti, molto più versatile di altri metodi, permette non solo di osservare direttamente i ‛lineamenti' di una molecola attraverso le interazioni dei suoi nuclei, ma anche di descriverne la disposizione nello spazio: in altri termini consente di determinare sia la struttura sia la stereochimica molecolare (v. stereochimica). Oggi la determinazione della struttura di una sostanza organica, per quanto complessa, non rappresenta più un grosso problema: rientra nella normale routine di un laboratorio di risonanza. L'esperienza acquisita in questo campo e lo sviluppo di spettrometri ad alto campo, operanti con magneti superconduttori, consentono oggi di affrontare problemi ancor più complessi, quali la determinazione della struttura e della dinamica di molecole di interesse biologico o lo studio in vivo di fenomeni biochimici e fisiologici.

2. La spettroscopia protonica: applicazioni all'analisi strutturale di sostanze naturali.

Un esempio di determinazione strutturale è mostrato nelle figg. 1 e 2, dove sono riprodotti gli spettri protonici della daunomicina (1) e di un suo frammento (2). Questa sostanza naturale, estratta da miceli di Streptomyces peucetius, mostrava un'attività antitumorale così intensa e specifica da indurre il gruppo di chimici che vi lavoravano a intraprenderne lo studio. Oggi essa rappresenta, insieme al suo analogo adriamicina, il farmaco più potente nella terapia dei tumori. La determinazione di una struttura come questa, prima dell'avvento della spettroscopia RMN, avrebbe richiesto molti anni di lavoro. Vediamo a titolo di esempio la via seguita per questa analisi strutturale.

Ricavata la formula minima C₂₇H₂₉O₁₀N dai dati analitici (percentuali di carbonio, idrogeno e azoto) e mediante spettrometria di massa, e identificato il cromoforo dell'antrachinone (i tre anelli aromatici fusi linearmente) con l'esame dello spettro UV, si sono ottenuti per idrolisi uno zucchero e un prodotto, C₂₁H₁₈O₈, detto daunomicinone. Questo, per metilazione degli OH, ha dato un composto, (2), il cui spettro RMN è riportato nella fig. 2. Da esso si possono trarre tutte le informazioni per definire la struttura, considerando che lo spettro IR ha indicato la presenza di un gruppo chetonico alifatico −C−CO−C. Un gruppo −COCH₃ è infatti presente a 2,40 δ, inoltre si hanno 4 −OCH₃, di cui uno alifatico a frequenza più bassa (3,56 δ), ancora un −OH libero (alcolico, a 5,70 δ) e un idrogeno a 4,92 δ, che presenta due costanti di accoppiamento (J_A′′X = 3,5 Hz e J_B′′X = 2,5 Hz); le stesse si ritrovano nelle due paia di doppietti simmetrici centrati a 1,87 δ e 2,42 δ (H_A′′ e H_B′′). I due doppietti di H_B′′ sono complicati da un'altra piccola costante di 1 Hz, che si ritroverà anche nel segnale a 3,22 δ; la separazione più grande (J_{A′′B′′} = 15 Hz) indica un accoppiamento geminale. Questi dati, unitamente ai valori degli shifts, indicano una sequenza −O−CHCH₂−C−; sul carbonio adiacente al −CH₂− non possono stare protoni per l'assenza di ulteriori accoppiamenti. I due idrogeni che mancano per chiudere l'anello saturo (anello di destra nella formula) costituiscono i due doppietti centrati a 3,02 e 3,22 δ, le cui righe esterne sono molto meno intense di quelle centrali. La costante di 18,5 Hz indica anche in questo caso che i due idrogeni sono geminali, e l'assenza di accoppiamenti vicinali (la piccola interazione di 1 Hz avviene attraverso quattro legami) permette di completare la sequenza. Restano tre idrogeni aromatici che sono responsabili del complesso assorbimento tra 7,8 e 8,1 δ. La complessità di uno spettro RMN dipende dal rapporto tra shift e costante di accoppiamento Δν/J: solo se questo rapporto è grande lo spettro è facilmente analizzabile. Ma poiché gli shifts sono direttamente proporzionali alla radiofrequenza, mentre le J ne sono indipendenti, è chiaro che aumentando Δν si potrà avere una semplificazione dello spettro. Nella parte superiore della fig. 2 è riportato l'assorbimento dei tre protoni aromatici a un campo più elevato; si leggono facilmente due costanti tra protoni in posizione orto (J_AB = J_BC = 7,8 Hz) e una tra protoni in meta (J_AC = 1,8 Hz). Questo ha permesso di stabilire la sequenza degli idrogeni sull'anello e quindi di completare la struttura del daunomicinone.

L'altro frammento ottenuto dall'idrolisi dell'antibiotico, una sostanza zuccherina non nota, è stato analizzato analogamente; i segnali dei suoi protoni sono facilmente identificabili nello spettro della daunomicina (v. fig. 1) NH, H-1′, CH₂-2′, H-3′, H-4′, H′5 e il gruppo metilico a 1,28 ppm (Me-5′). I valori delle costanti di accoppiamento che legano questi nuclei, anch'esse riportate nella figura, hanno permesso di dedurre non solo la loro sequenza sull'anello dello zucchero, ma anche la loro orientazione reciproca nello Spazio. I due ultimi sottili segnali a 13,86 e 13,15 ppm appartengono ai protoni dei gruppi OH sull'anello dell'antrachinone, impegnati ciascuno in un forte legame a idrogeno (chelazione), che provoca un aumento considerevole della loro frequenza di assorbimento. Il punto di attacco dello zucchero sul daunomicinone è stato infine identificato in base al valore dello shift di H-7 nei composti (1) e (2) in confronto con il pentaacetilderivato della daunomicina. La struttura dell'antibiotico è così completa.

Le prestazioni di questa tecnica offrono dunque vantaggi talmente evidenti che non hanno bisogno di ulteriori commenti, ma un punto va sottolineato. L'importanza di poter risolvere nel più breve tempo possibile la struttura di una sostanza nuova, capace di esplicare un'interessante attività biologica, non è solo economica; infatti tale conoscenza permette ai chimici di apportare delle modifiche alla struttura della sostanza in esame, creando per sintesi nuovi farmaci con attività potenziata e con sempre minore tossicità.

Una tecnica normalmente usata per l'analisi spettrale, e quindi applicata soprattutto nel caso di strutture complesse come gli antitumorali citati (v. fig. 1), è il ‛disaccoppiamento di spin' (v. risonanza magnetica nucleare: Applicazioni chimiche, suppl.). L'utilità di questo metodo per semplificare gli spettri è subito evidente, ma l'importanza che esso ha avuto nell'analisi strutturale dipende dal fatto che la perturbazione così indotta è selettiva e specifica e permette di identificare sia la sequenza dei protoni nella molecola, sia i legami che li coinvolgono (si veda l'esempio dell'antitumorale daunomicina, nella fig. 1, e anche il caso riportato nella fig. 3).

A partire dai valori delle costanti di accoppiamento, si può determinare la stereochimica e la conformazione di sostanze complesse (v. stereochimica; v. molecole). L'esempio riportato nella fig. 3 riguarda un alcaloide isolato da una pianta (della specie Uncaria) insieme ad altri stereoisomeri. I centri chirali sono 4: C-3, C-15, C-19 e C-20. Nota la configurazione assoluta al C-15 dalla biogenesi, la chiralità degli altri centri è stata determinata utilizzando i dati spettrali riportati nella fig. 3.

Ciò ha permesso di identificare i vari stereoisomeri, ad esempio di distinguere la roxburghina E (4) dalla roxburghina D (3) e di studiare l'equilibrio conformazionale in soluzione (v. schema 1): la conformazione predominante è indicata come (4a).

3. La spettroscopia del ¹³C e le sue applicazioni alla biosintesi di sostanze naturali.

L'applicazione della spettroscopia di risonanza del carbonio ha preso l'avvio negli anni settanta, quando lo sviluppo delle nuove tecniche ‛a impulso' e l'impiego dei primi calcolatori direttamente allacciati allo spettrometro hanno consentito di osservare la risonanza dell'isotopo ¹³C, la cui abbondanza naturale è 1,1%, rispetto all'isotopo dominante ¹²C. Lo spin del nucleo ¹³C è 1/2, come quello del protone, ma il suo momento magnetico è circa 4 volte più piccolo; così anche il rapporto giromagnetico del ¹³C (γ_13C) è 4 volte più piccolo di quello del protone. Poiché la sensibilità è proporzionale al cubo di γ, ne risulta che la sensibilità del ¹³C è circa 1/64 di quella dell'idrogeno. Tenuto conto che l'abbondanza naturale è 1,1%, la sensibilità risulta circa 1/6.400 rispetto a quella dell'idrogeno. Inoltre il tempo di rilassamento è più lungo (un minuto e anche più) e diventa perciò difficile eliminare fenomeni di saturazione, con conseguenti distorsioni dei segnali. Per questo motivo, osservare la risonanza del carbonio in abbondanza naturale, cioè in campioni non arricchiti in ¹³C, risultava, con gli spettrometri tradizionali ‛a onda continua', estremamente difficoltoso. Nella tecnica a onda continua viene utilizzato, come sorgente di radiofrequenze per l'irradiazione del campione, un campo magnetico oscillante H₁, molto debole (circa 10^-7 tesla) e lentamente variabile. Con questo sistema i nuclei entrano in risonanza in momenti diversi, cioè quando H₁ raggiunge di volta in volta il valore della frequenza di risonanza propria di ciascuno di loro. Nella tecnica ‛a impulso', invece, il campo H₁ è molto più intenso (circa 2 × 10^-2 tesla), comprende una larga banda di frequenze (dell'ordine dei kHz), ma viene applicato per un tempo molto breve; ogni impulso per circa 1 μs. Si ha come risultato che tale campo fa risuonare tutti i nuclei contemporaneamente ed essi contemporaneamente mandano i loro segnali di assorbimento. Come sempre accade quando si sovrappongono più segnali con frequenze diverse, si ottiene una figura di interferenza (v. fig. 4): lo spettro è cioè una misura, nel tempo, del segnale risultante, il quale si affievolisce, più o meno lentamente, dopo che l'impulso è stato tolto.

Uno spettro come quello della fig. 4A contiene tutte le informazioni dei nuclei (shifts, costanti di accoppiamento e tempi di rilassamento), ma esse non sono facilmente deducibili, perciò tale spettro viene trasformato matematicamente da un calcolatore (usando una ‛trasformata di Fourier') nello spettro di assorbimento tradizionale (v. fig. 4B).

L'aspetto più importante di questa tecnica sta nel fatto che possono essere utilizzati più impulsi ad appropriati intervalli di tempo, sicché più spettri di interferenza possono essere addizionati nella memoria del calcolatore e alla fine trasformati. Si può avere dunque la somma di migliaia di spettri uguali, e anche nuclei a bassissima sensibilità come il ¹³C possono rivelare i loro segnali.

È facile intuire quale importanza rivesta per il chimico organico e per il biochimico la spettroscopia del carbonio, permettendo loro di vedere tutti o quasi tutti gli atomi di carbonio delle molecole di cui si occupano, il che equivale a determinarne lo scheletro. Un aspetto importante è che gruppi funzionali quali il C=O, il −COOH e altri contenenti carboni quaternari, perciò senza idrogeni direttamente legati e quindi senza parametri di risonanza protonica, mostrano invece shifts ben caratteristici negli spettri ¹³C. Inoltre gli shifts sono distribuiti lungo 250 ppm e gli spettri sono estremamente semplici, perché gli accoppiamenti ¹³C-¹³C non sono rilevabili nei campioni in abbondanza naturale, data la bassissima probabilità di trovare due nuclei ¹³C adiacenti. Gli accoppiamenti con i protoni sono invece visibili, come si può notare dalla struttura fine dei segnali della piridina (v. fig. 5A). La struttura fine può essere eliminata usando un'intensa sorgente di radiofrequenze a banda larga, che disaccoppia contemporaneamente tutti i nuclei: i segnali dei carboni in tal caso diventano dei singoletti (v. fig. 5B). Questa tecnica è analoga al disaccoppiamento selettivo tra protone e protone; qui l'intensità del campo oscillante è più elevata, perché la sua banda di frequenze deve irradiare tutti i protoni della molecola, per poterli disaccoppiare tutti contemporaneamente dai rispettivi carboni.

Alcuni esempi di spettri ¹³C, in cui si vedono tutti i segnali degli atomi di carbonio separati, sono riprodotti nelle figg. 6 e 7. È sorprendente come nella molecola del colesterolo (5) atomi di carbonio strutturalmente simili rivelino frequenze di risonanza così differenziate.

Lo studio di importanti sostanze naturali, quali terpeni, steroidi, ormoni, alcaloidi, coenzimi (v. fig. 7), si è avvalso largamente della risonanza del carbonio.

Tra le applicazioni più interessanti della risonanza del carbonio vi sono lo studio della biosintesi di sostanze naturali (v. biosintesi) e i più recenti studi del metabolismo cellulare in vivo (v. cap. 5), che permetteranno di ottenere importanti e sempre più dettagliate informazioni sui processi biochimici negli organismi viventi.

Dagli anni cinquanta in poi c'è stata una grande fioritura di ricerche nel campo della biosintesi di sostanze provenienti dal mondo vegetale e animale, che hanno portato alla conoscenza dei precursori di numerose sostanze naturali, dei loro prodotti intermedi e dei meccanismi della loro formazione. Tra i diversi metodi impiegati in queste ricerche la risonanza del carbonio è il più semplice e diretto, certamente quello che dà il maggior numero di informazioni dettagliate e precise. Infatti molecole marcate con ¹³C vengono somministrate agli organismi in studio e da questi utilizzate e incorporate nelle molecole del metabolita in posizioni che saranno facilmente identificate da uno spettro di risonanza del ¹³C, evitando la noiosissima procedura di demolire il prodotto marcato e separare i vari frammenti. Un esempio è riportato nella fig. 8.

La granaticina (8) è un antibiotico isolato da vari ceppi di Streptomyces, il cui precursore, la diidrogranaticina (7) mostra, nella forma del suo metil-estere, lo spettro ¹³C della fig. 8A, in cui tutti gli atomi di carbonio sono stati identificati nei rispettivi segnali. Colture di Streptomyces nutrite con acetato marcato al metile, ¹³CH₃COONa, ed estratte in modo analogo alle colture normali, hanno portato a un prodotto marcato (7), il cui spettro RMN (v. fig. 8B) mostra chiaramente che gli atomi di carbonio 1, 3, 5, 7, 9, 11, 13 e 15 si sono arricchiti in ¹³C in media dal 3 al 5% (i segnali sono molto più intensi di quelli in abbondanza naturale). Questi atomi di carbonio, segnati con un asterisco nelle formule dello schema 2, provengono dai gruppi metilici, arricchiti in ¹³C, di otto unità di acetato.

La sequenza alternata dell'incorporazione indica che la biosintesi procede, seguendo la nota ‛regola dell'acetato', attraverso la formazione di un polichetone, da cui prende origine il sistema benzochinonico (6), mentre i sei carboni da C-1′ a C-6′, che non mostrano alcuna incorporazione di acetato, provengono da una molecola di glucosio. Esperimenti con glucosio marcato in varie percentuali hanno dimostrato infatti che una unità di glucosio viene incorporata per formare la parte della molecola posta a sinistra nello schema 2; il gruppo 6′-CH₃, ad esempio, si origina dal gruppo −CH₂OH dello zucchero. Il glucosio subisce una serie di ossidoriduzioni enzimatiche prima di legarsi al sistema aromatico, tramite gli atomi C-1′ e C-4′. L'ultimo stadio della biosintesi della granaticina è la formazione dell'anello pentaatomico, per ossidazione e disidratazione, che non sembra però coinvolgere ossigeno molecolare.

4. Studio della conformazione delle biomolecole e della dinamica molecolare.

Una caratteristica comune a tutte le biomolecole (zuccheri, proteine, coenzimi, nucleotidi, DNA, RNA) è la grande mobilità conformazionale (v. molecole). In altre parole queste molecole non sono dei sistemi rigidi, con una certa forma, come la spettroscopia a raggi X ci ha abituato a considerarle, ma delle entità molto flessibili, che possono assumere le più svariate forme, per rotazione intorno ai loro legami. Questa mobilità interna si aggiunge ai moti traslazionali e rotazionali che le molecole compiono per effetto dell'agitazione termica.

La mobilità molecolare è importante quanto il tipo di struttura ai fini delle funzioni che le biomolecole svolgono nell'ambiente cellulare. Anche l'attività biologica di sostanze quali farmaci, fitoregolatori, dolcificanti, sostanze amare, aromi è strettamente correlata alle proprietà conformazionali, oltre che strutturali, sia della sostanza attiva sia del recettore; non solo, ma la conformazione di entrambi può variare a seconda della loro funzione. La superficie di un recettore, ad esempio di una grossa proteina come un enzima, può essere estremamente flessibile in alcune sue parti, e in altre invece più rigida, ripiegata su se stessa a formare tasche o canali. Questa apparente irregolarità, che può sembrare casuale, condiziona in modo molto critico l'attività biologica: permette, ad esempio, a una molecola più piccola, che può essere sia estranea all'organismo (per es. un farmaco) sia endogena (ormoni, neurotrasmettitori), di attraversare le zone mobili e di infilarsi in questi canali fino a raggiungere il sito di legame; d'altra parte, altre molecole (antagoniste) possono bloccare l'ingresso a questi canali, modificando la conformazione della proteina o di una parte di essa. L'immagine della ‛chiave e serratura', dunque, non è più sufficiente per interpretare il meccanismo d'azione delle sostanze biologicamente attive, sia esogene sia endogene.

Lo studio delle proprietà stereodinamiche delle molecole è affascinante e di grande attualità, per le prospettive che apre alla biologia molecolare, e la spettroscopia RMN, che permette di osservare le molecole in soluzione, si presta assai bene a questo tipo di studi.

Un altro settore in cui la spettroscopia RMN trova sempre maggiori applicazioni è quello della ricerca, destinata a diventare sempre più ‛mirata', di nuovi prodotti sintetici utili all'uomo. Per quel che riguarda molti farmaci, si sa tutto sulla loro azione farmacologica, ma quasi nulla sul loro meccanismo d'azione a livello molecolare; tra i tanti ricordiamo le fenotiazine (9) e le dibenzazepine (10), psicofarmaci di largo uso, noti da tempo per la loro attività sul sistema nervoso centrale.

La loro struttura è costituita da una parte rigida (gli anelli aromatici) e da una parte flessibile, la catena legata all'azoto dell'anello centrale. Anche la parte rigida però è dotata di moti interni: i due anelli benzenici oscillano su e giù rispetto al piano ‛ideale' della molecola, con un moto paragonabile a quello delle ali di una farfalla. La catena può assumere diverse forme o conformazioni, tra le quali le più stabili, quindi le più ‛probabili', sono indicate nella fig. 9: una distesa o trans-trans, l'altra un po' ripiegata su se stessa, o gauche-trans.

Dai dati RMN, che qui non discuteremo, si è potuto dimostrare che, a pH acido, la forma predominante in soluzione è quella piegata gauche-trans, mentre in ambiente alcalino le due forme sono presenti in egual misura. Anche la mobilità della catena varia nei due casi: ciò si deduce dai valori dei tempi di rilassamento degli atomi di carbonio indicati nello schema 3.

I tempi di rilassamento sono correlati alla dinamica molecolare, e quindi anche ai moti interni delle molecole, da relazioni complesse, che, per soluzioni diluite, possiamo esprimere nella forma semplificata

dove γ_C e γ_H sono i rapporti giromagnetici del carbonio e dell'idrogeno, N il numero dei protoni direttamente legati a ogni carbonio e r la distanza C−H. Dalla formula si vede che il tempo di rilassamento T₁ è inversamente proporzionale a τ_c (tempo che caratterizza il moto) e quindi direttamente proporzionale alla velocità del moto stesso. Valori piccoli di T₁, espressione di un rilassamento efficace, corrispondono dunque a moti lenti. Nei nostri farmaci, a pH alcalino, l'incremento di valore da un estremo all'altro della catena indica un moto di tipo segmentale: la ‛coda' della catena, −N(CH₃)₂, si muove cioè più velocemente. In ambiente acido l'azoto terminale è protonato e funziona da ‛ancora': i tempi infatti sono tra loro simili e inferiori a quelli delle basi; in queste condizioni la mobilità è molto ridotta e non c'è nessuna evidenza di moto segmentale. Benchè queste sostanze siano note da anni, non si conosce ancora quasi nulla circa il loro meccanismo di azione a livello molecolare.

È stato dimostrato recentemente che farmaci antipsicotici, quale la clorpromazina, sono inibitori degli enzimi adenilatociclasi e fosfodiesterasi e che si legano alla proteina calmodulina, attivatore di questi enzimi. Questa proteina, la cui struttura non è del tutto nota, lega facilmente 4 atomi di calcio ed è attiva in questa forma. La calmodulina svolge una funzione complessa e multiforme e controlla l'attività di molti enzimi. Quando una sostanza antipsicotica, ad esempio la clorpromazina, si lega in vitro alla calmodulina, si ha una variazione conformazionale della proteina, messa in evidenza mediante RMN; si è anche potuto rilevare che ciò provoca un drammatico effetto sul sito di coordinazione del calcio. Questa variazione conformazionale consente di esporre un sito adatto al legame col farmaco, legame che si ritiene presumibilmente di natura idrofobica. La presenza del farmaco già legato, o in competizione, nella stessa zona, impedirebbe all'enzima l'interazione con il suo attivatore, la calmodulina. Nella fig. 10 è illustrata questa ipotesi di meccanismo.

I risultati di queste ricerche, peraltro ancora in corso, sono stati ottenuti utilizzando sia la risonanza del protone, sia quella del calcio (isotopo ⁴³Ca) e del cadmio ¹¹³Cd, nucleo che ‛mima' il calcio e, avendo spin 1/2, ha linee più sottili e si presta meglio a uno studio RMN.

5. La risonanza del fosforo e gli sviluppi della spettroscopia in vivo.

Il fosforo ³¹P, possedendo spin 1/2 e abbondanza naturale del 100%, è stato uno dei nuclei studiati fin dalle origini della risonanza magnetica nucleare, ma le applicazioni della spettroscopia del fosforo alla chimica sono state scarse e occasionali, data la presenza relativamente bassa di atomi di fosforo nei composti organici. Assai attraente risulta invece questo nucleo nello studio dei campioni biologici, perché gli spettri ³¹P-RMN sono relativamente semplici (v. fig. 11) e possono essere ottenuti in soluzione acquosa senza dover ricorrere a esperimenti di disaccoppiamento di spin, che rischierebbero di danneggiare il campione a causa dell'alta temperatura che viene raggiunta per effetto delle correnti indotte nelle soluzioni acquose dal campo magnetico elevato usato per disaccoppiare. Questo nucleo inoltre ha un largo campo di shifts (circa 30 ppm per i composti di interesse biologico) ed è sensibile al pH, mentre sono relativamente poche le diverse situazioni strutturali in cui l'atomo di fosforo è coinvolto nelle molecole biologiche. Perciò, nonostante la sensibilità sia circa 1/15 rispetto a quella del protone, la spettroscopia ³¹P-RMN può fornire importanti informazioni per lo studio della biochimica e della fisiologia dei sistemi viventi. Se si considera il numero elevato di processi biologici in cui il fosforo è coinvolto, è comprensibile l'interesse crescente rivolto a queste tecniche da biochimici, biologi e fisiologi. I segnali ³¹P dei gruppi fosfato legati a composti organici diversi, quali zuccheri, intermedi della glicolisi, nucleotidi, possono essere facilmente risolti e identificati. Inoltre lo stato di ionizzazione dei fosfati e le loro interazioni con ioni metallici, come il magnesio, influenzano gli shifts ³¹P. Così, ad esempio, i tre atomi di fosforo dell'ATP (11) assorbono a frequenze diverse (v. fig. 11), in funzione del loro diverso intorno strutturale. La loro identificazione si basa sulla molteplicità dei segnali: il P_β è un tripletto per l'accoppiamento attraverso due legami con i due nuclei di fosforo adiacenti, il P_γ e il P_α, sono entrambi doppietti per l'interazione con il P_β, ma il segnale del fosforo in α è complicato dall'accoppiamento con i due protoni sul carbonio 5′ del ribosio adiacente.

Negli ultimi dieci anni l'introduzione delle nuove tecniche a impulso con trasformata di Fourier (v. cap. 3) e lo sviluppo dei calcolatori e dei magneti ad alto campo hanno portato gli spettrometri commerciali a un aumento incredibile di sensibilità, tanto da consentire misure RMN su sistemi viventi. I materiali biologici sono costituiti in larga parte da sostanze solide, che danno segnali molto larghi, e in parte da soluzioni acquose. In esse sono disciolte sostanze costituite da molecole di piccole dimensioni, che godono pertanto di una discreta mobilità, tale da permettere l'osservazione di segnali RMN abbastanza risolti. Le grosse molecole proteiche invece, avendo mobilità ridotta, e quindi tempi di rilassamento brevi, danno segnali larghi, che si perdono, come quelli delle molecole solide, nel rumore di fondo. Il fosforo ³¹P, contenuto nelle molecole mobili dell'ATP, del NAD⁺ e di nucleotidi analoghi, degli zuccheri mono- e difosfati e di altri piccoli metaboliti, è il nucleo più adatto, per i motivi sopra esposti, per misure in vivo in abbondanza naturale.

Per esempio nella fig. 12 è riportato (a) lo spettro ³¹P-RMN ottenuto da semi in fase di incipiente germinazione, immersi in acqua e perfusi con aria. Sono chiaramente visibili, accanto all'intenso assorbimento del fosfato inorganico, P_i, i segnali dei tre atomi di fosforo dell'ATP e quello del glucosio-6-fosfato. Lo shift dei fosfati, come si è già detto, è sensibile allo stato di ionizzazione e quindi al pH dell'ambiente; in particolare il fosfato inorganico, avendo pK = 6,9, è fortemente dipendente dal pH, intorno al valore 7. Per questo lo shift del P_i citoplasmatico può essere usato, mediante opportune curve di taratura, per determinare il pH intracellulare. Anche il glucosio-6-fosfato mostra una forte dipendenza dal pH nell'intervallo fisiologico. Una misura assoluta mediante RMN è accurata entro 0,2 unità di pH, ma variazioni relative anche più piccole possono essere valutate facilmente. Non esistono altri metodi di misura altrettanto validi, per cui tali fosfati sono considerati dei veri e propri indicatori naturali del pH cellulare.

Gli shifts degli atomi di fosforo in γ e β nell'ATP variano (2 ÷ 3 ppm) quando esso è legato al magnesio. Esperimenti in vitro e in vivo hanno dimostrato questa dipendenza e i valori osservati in vivo indicano che l'ATP nelle cellule viventi esiste principalmente come complesso Mg²⁺-ATP.

Osserviamo che cosa succede nei semi se si interrompe il flusso di aria (v. fig. 12, b): diminuiscono fino quasi a scomparire i segnali dell'ATP, mentre aumenta il fosfato inorganico. In condizioni di ipossia la sintesi dell'ATP è estremamente ridotta, mentre compaiono i segnali dell'adenosindifosfato (ADP), che nei tessuti aerobici è virtualmente assente.

Un'altra caratteristica unica della spettroscopia in vivo è la possibilità di osservare separatamente i diversi ‛compartimenti' di metaboliti che sono presenti nell'ambiente cellulare; ad esempio nei tessuti adulti, le cui cellule sono vacuolate, si osservano due segnali del fosfato inorganico, P_i che provengono dal citoplasma e dal vacuolo. Così nello spettro (a) della fig. 13, ottenuto da apici di radici di pisello, le frequenze del P_i citoplasmatico (2,73 ppm) e del P_i vacuolare (0,98 ppm) indicano una notevole differenza di pH tra i due compartimenti. Inoltre, se le piantine vengono nutrite in ambiente ricco di fosfato inorganico, il segnale del fosforo vacuolare aumenta, mentre il P_i citoplasmatico e anche l'ATP restano approssimativamente costanti (v. fig. 13, b). Questo risultato è di notevole interesse, perché mostra non solo l'esistenza dei due diversi compartimenti cellulari, ma anche le loro diverse funzioni: il P_i citoplasmatico ha un ruolo centrale nel controllo del metabolismo cellulare, perché la sua concentrazione influenza il metabolismo e quindi lo sviluppo della pianta. Invece la concentrazione del P_i nel vacuolo può variare in accordo con la disponibilità esterna del fosfato. La crescita degli apici di radici di pisello non sembra influenzata per circa 10 ÷ 15 giorni dalla quantità di fosfato esterno, che verrebbe dunque accumulato come riserva nel vacuolo. Da questi primi esperimenti sembra che il fosfato inorganico venga trattenuto nel citoplasma contro un gradiente di concentrazione rispetto al vacuolo; sarebbe la differenza di pH nei due compartimenti a favorire il movimento preferenziale dell'anione HPO4^2- verso il vacuolo. La concentrazione stazionaria del P_i nel citoplasma contribuirebbe a mantenere costante la velocità di idrolisi dell'ATP e quindi a tenere sotto controllo il metabolismo.

I primi esperimenti in vivo con organi intatti sono stati eseguiti nei laboratori di Pasadena e Oxford nel 1973 e nel 1974, rispettivamente su eritrociti e su tessuti muscolari, determinando per la prima volta il pH intracellulare e seguendo il metabolismo del muscolo di un arto di ratto direttamente mediante la risonanza del ³¹P. Gli spettri di quest'ultimo esperimento sono riportati nella fig. 14. Anche i tessuti muscolari mostrano chiaramente visibili i segnali dei piccoli metaboliti: del glucosio-6-fosfato, parzialmente sovrapposto a quello più largo dei fosfolipidi (I), del fosfato inorganico (II), del creatinfosfato (III) e i tre segnali dell'ATP (IV, V e VI). Dopo un certo tempo (v. fig. 14, c e d), il segnale del creatinfosfato diminuisce, mentre aumenta lentamente il fosfato inorganico; quando il creatinfosfato è scomparso, diminuisce anche l'ATP e aumenta vistosamente il fosfato inorganico. Questo esperimento dimostra la funzione dell'enzima creatinchinasi quale regolatore del livello di ATP nei muscoli. Normalmente l'ATP utilizzato per il lavoro muscolare o chimico viene rigenerato attraverso il ciclo di Krebs, ma in assenza di ossigeno le cellule provvedono iniziando la glicolisi anaerobica, durante la quale si forma, quale prodotto secondario, acido lattico, responsabile della diminuzione del pH cellulare. Questa situazione non è tollerata a lungo dalle cellule, così che esse sopperiscono per breve tempo alla forte domanda di ATP prelevando dal creatinfosfato l'acido fosforico necessario. Quando questo substrato è finito (v. fig. 14, d), la glicolisi anaerobica procede con diminuzione del pH intracellulare da circa 7,1 a circa 6,2 dopo 160 minuti (questa diminuzione è misurata dalla variazione di shift del P_i, il cui segnale si sposta progressivamente verso le basse frequenze). Il muscolo col tempo consuma tutto l'ATP e il fosfato inorganico (Il) aumenta corrispondentemente.

6. Prospettive future.

Recentemente sono comparsi in letteratura numerosi studi di RMN in vivo su organismi unicellulari quale Escherichia coli, su granuli cromaffini delle surrenali, su mitocondri del fegato, su cellule tumorali e su tessuti muscolari. Si è giunti infine a osservare, con strumenti di opportune dimensioni, animali vivi e anche l'uomo (v. tomografia a risonanza magnetica nucleare, suppl.). Mentre le applicazioni più interessanti della risonanza del fosforo (³¹P-RMN) riguardano la fisiologia vegetale, per gli studi sul metabolismo animale sembra più promettente, in una prospettiva futura, la risonanza del carbonio (¹³C-RMN). Gli esperimenti di ¹³C-RMN vengono di solito eseguiti su substrati arricchiti in ¹³C: ad esempio, colture cellulari vengono trattate con [1-¹³C] glucosio o [1,3-¹³C] glicerolo; piante a certi stadi di crescita vengono immesse in ambiente di ¹³CO₂. I composti arricchiti in ¹³C vengono metabolizzati dalle cellule, quindi i segnali ¹³C di metaboliti intermedi e finali possono essere osservati e seguiti durante i loro percorsi nei vari comparti cellulari, permettendo la determinazione della cinetica di reazione e lo studio del meccanismo di molti processi biologici.

Anche la risonanza protonica ha subito un rilevante sviluppo con i nuovi magneti ad alto campo e le nuove tecniche a disposizione, che si avvalgono di calcolatori sempre più potenti. È stato possibile seguire a livello metabolico, mediante ¹H-RMN, ad esempio, i processi di differenziazione di cellule leucemiche di Friend. Il campo magnetico elevato, che raggiunge 11,74 tesla negli spettrometri a 500 MHz oggi in commercio, è indispensabile per la risonanza protonica delle biomolecole, essendo gli shifts compresi in un intervallo assai ristretto. Poiché le frequenze di assorbimento sono proporzionali all'intensità del campo applicato, è evidente il vantaggio di uno strumento ad alto campo. D'altra parte, l'impiego di calcolatori sempre più sofisticati permette non solo di aumentare moltissimo la sensibilità, ma di utilizzare con profitto le molteplici tecniche di doppia risonanza. Tra queste sono da citare, oltre al disaccoppiamento di spin, l'‛effetto Overhauser' (NOE) e il saturation transfer (trasferimento di saturazione). Il primo metodo, se applicato quantitativamente, permette di misurare le distanze interatomiche in fase liquida, con la stessa precisione della spettroscopia a raggi X per la fase solida; col secondo metodo si può determinare la cinetica di processi biologici, anche in vivo, ad esempio misurare l'attività ATPasica, utilizzando il ³¹P.

L'RMN ha inoltre acquisito una nuova dimensione, nel senso più letterale della parola nella fig. 15 è riportato lo spettro in due dimensioni dell'amminoacido senna. La seconda dimensione permette di separare quelle componenti che nello spettro convenzionale sono sovrapposte, ad esempio costanti di accoppiamento e shifts (v. fig. 1 5) oppure shifts di nuclei tra loro accoppiati (v. fig. 16). Gli spettri di molecole più complesse vengono di solito rappresentati con mappe di livello, come nella fig. 16. La seconda dimensione può essere ottenuta con vari metodi, per esempio si può introdurre un secondo impulso di radiofrequenza, prima che il rilassamento dal primo impulso sia completo. Una trasformata di Fourier fornisce lo spettro convenzionale, una seconda trasformata di Fourier degli stessi dati fornisce la seconda dimensione.

In generale, quasi tutto quello che si fa con la spettroscopia in due dimensioni (RMN-2D) si può anche fare con la spettroscopia convenzionale, ma la prima è più veloce e più semplice. Oggi l'uso dell'RMN-2D per piccole molecole è già di routine nei laboratori di sintesi chimica, come nell'industria farmaceutica, ma l'area di maggior interesse e prospettive future è l'applicazione in biochimica. L'analisi conformazionale di proteine e nucleotidi in soluzione è appena cominciata. Gli spettri protonici di queste sostanze sono molto complessi, come si può osservare nella fig. 17, dove è riportato lo spettro del citocromo c. Solo alcuni segnali sono separati dalla confusa zona centrale (che comprende quasi tutti gli atomi d'idrogeno della molecola), grazie alla presenza di un atomo di ferro paramagnetico nell'anello porfirinico dell'eme: il ferro imprime un forte shift ai gruppi vicini, per interazione dei loro nuclei con il suo elettrone spaiato. Il citocromo c è un importante enzima della catena respiratoria, responsabile del trasporto di elettroni dalla citocromoriduttasi alla citocromossidasi. Il meccanismo di questo trasporto non è tuttavia ancora noto e si attendono dalle ricerche RMN nuove informazioni sia sul trasporto elettronico, sia sulla conformazione (struttura terziaria) della proteina nelle vicinanze dell'eme.

La maggior parte delle proteine, però, non possiede un atomo paramagnetico, per cui in questi casi l'RMN-2D si impone. Nella fig. 16 è riportato lo spettro ¹H-RMN in due dimensioni della parvalbumina, estratta da muscoli di carpa. Le parvalbumine, proteine che legano il calcio, sono presenti in grandi quantità nei muscoli, ma la loro funzione non è ancora stata determinata. Nei Vertebrati il processo di contrazione muscolare è strettamente correlato al legame degli ioni calcio con la troponina, una proteina a più elevato peso molecolare, la cui struttura, nei siti di coordinazione del calcio e in quelli limitrofi, è risultata però assai simile a quella delle parvalbumine. Risultati molto recenti indicano che la struttura terziaria di queste proteine è strettamente dipendente dal legame con gli ioni calcio; forti variazioni conformazionali sono state infatti osservate in assenza di calcio, mediante ¹He ⁴³Ca-RMN.

Infine un importante contributo dell'RMN alla comprensione dei complicati processi naturali è lo studio delle interazioni ioniche nei sistemi biologici. Se la vita è nata nell'acqua, si può facilmente immaginare che l'evoluzione delle macromolecole biologiche debba essersi adattata alla presenza di ioni nell'ambiente acquoso. Infatti molte proteine contengono cationi, c'è una grande famiglia di metalloenzimi e ioni sono coinvolti nella trasmissione degli impulsi nervosi, nelle contrazioni muscolari e nel trasporto intra- ed extracellulare. Inoltre i cationi possono agire come attivatori di enzimi: è noto che almeno 60 enzimi sono attivati solo da cationi monovalenti. Il ruolo degli anioni è meno documentato ma non meno importante. Le diverse concentrazioni intra- ed extracellulari di anioni Cl^-, HPO4^2-, HCO3^- osservate in alcune specie possono essere il risultato di un trasporto attivo attraverso la membrana cellulare. L'esistenza di una superficie anionica sulla molecola degli acidi nucleici ha un significato biologico assai grande. Infine alcuni enzimi (quali l'α-amilasi) sono attivati da anioni.

Sembra dunque che questo tipo di interazioni rientri in un generale modus operandi della natura. L'RMN è la tecnica più adatta per lo studio di questi problemi, perché può utilizzare, oltre a quelli già citati, i nuclei ²³Na, ³⁹K, ⁴³Ca, ¹¹³Cd, ⁵⁹Co, ²⁵Mg, ³⁵Cl, ³⁷Cl.

L'osservazione in vivo di segnali RMN degli ioni più comuni è già possibile, ma i problemi di interpretazione sono ancora enormi, per cui non c'è dubbio che le più importanti informazioni sulle interazioni ioniche nei sistemi biologici si otterranno ancora per lungo tempo da studi su modelli semplici.

Bibliografia.

Andersson, T., Drakenberg, T., Forsen, S., Thulin, E., Sward, M., Direct observation of the ⁴³Ca-NMR signals from Ca²⁺ ions bound to proteins, in ‟Journal of the American Chemical Society", 1982,CIV, pp. 576-580.

Arcamone, F., Cassinelli, G., Franceschi, G., Mondelli, R., Orezzi, P., Penco, S., Struttura e stereochimica della daunomicina, in ‟Gazzetta chimica italiana", 1970, C, pp. 949-989.

Arnone, A., Camarda, L., Cardillo, R., Fronza, G., Merlini, L., Mondelli, R., Nasini, G., Pyrek, J. St., ¹³C-NMR analysis of dihydrogranaticin methyl ester. A case of mixed biogenesis, in ‟Helvetica chimica acta", 1979, LXII, 1, pp. 30-33.

Cistaro, C., Merlini, L., Mondelli, R., Nasini, G., NMR spectra, absolute configuration and conformational analysis of the indole alkaloids roxburghine B, C and E, in ‟Gazzetta chimica italiana", 1973, CIII, pp. 153-169.

Gorenstein, D.G., Phosphorus-31 NMR, New York 1984.

Gunther, H., NMR spectroscopy, New York 1980.

Hoult, D.I., Busby, S. J. W., Gadian, D.G., Radda, G. K., Richards, R.E., Seeley, P. J., Observation of tissue metabolites using ³¹P nuclear magnetic resonance, in ‟Nature", 1974, CCLII, pp. 285-287.

Lee, R.B., Ratcliffe, R.G., Phosphorus nutrition and the intracellular distribution of inorganic phosphate in pea root tips: a quantitative study using ³¹P-NMR, in ‟Journal of experimental botany", 1983, XXXIV, pp. 1222-1244.

Moon, R.B., Richards, J. H., Determination of intracellular pH by ³¹P magnetic resonance, in ‟The journal of biological chemistry", 1973, CCXLVIII, pp. 7276-7278.

Ragg, E., Fronza, G., Mondelli, R., Dynamic aspects of the stereochemistry of phenothiazines in solution. Part 2. Segmental motion and conformational analysis of the side-chain in promazines, in ‟Journal of the Chemical Society", Perkin Transaction II, 1982, pp. 1578-1591.

Shulman, R.G., Biological applications of magnetic resonance, New York 1979.

Sigel, H., Metal ions in biological systems. Calcium and its role in biology, vol. XVII, New York 1984.

Snipes, C.E., Chang, C., Floss, H.G., Biosynthesis of the antibiotic granaticin, in ‟Journal of American Chemical Society", 1979, CI, pp. 701-706.

Wilder, G., Macura, S., Kumar, A., Ernst, R.R., Wuthrich, K., Homonuclear two-dimensional ¹H-NMR of proteins, in ‟Journal of magnetic resonance", 1984, LVI, pp. 207-234.