Archimede, saliera di
Archimede, saliera di
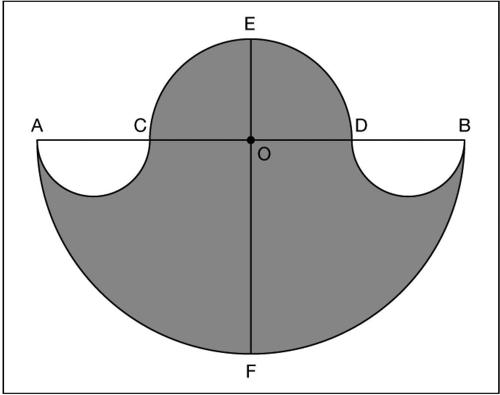
Archimede, saliera di figura piana studiata da Archimede. Si ottiene a partire da una semicirconferenza di centro O e diametro AB e da due arbitrari punti C e D del diametro simmetrici rispetto a O. Si costruiscono quindi tre semicirconferenze, l’una di centro O e diametro CD esterna alla semicirconferenza data, le altre di diametri AC e DB interne alla circonferenza data. La regione finita di piano delimitata dalle quattro semicirconferenze è la saliera di Archimede, così detta per la somiglianza con l’oggetto di uso quotidiano evocato dalla sua forma. Indicati con E e F i punti di intersezione della perpendicolare ad AB per O con le due semicirconferenze di centro O, si dimostra che l’area di tale saliera è uguale a quella del cerchio di diametro EF.