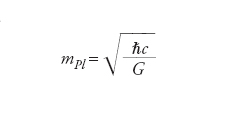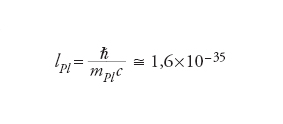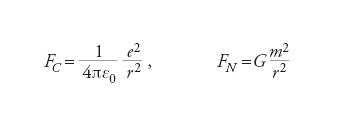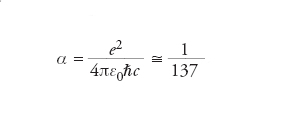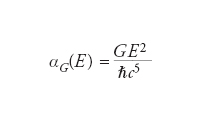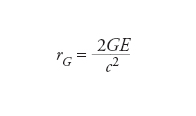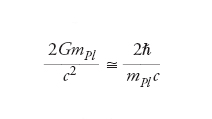scala di Planck
scala di Planck
Scala, relativa a diverse grandezze fisiche, alla quale i fenomeni quantistici diventano rilevanti per il campo gravitazionale. Combinando la costante di Planck h, o piuttosto la sua versione ridotta ℏ=h/2π, la velocità della luce c e la costante di gravitazione universale G, è possibile costruire una quantità detta massa di Planck e definita come
il cui valore numerico è mPl≅2×10−8 kg, nel sistema SI, o mPl≅1,2×1019 GeV/c2, in unità più comunemente utilizzate nella fisica delle particelle elementari. La massa di Planck definisce a sua volta un’energia, detta energia di Planck,
EPl = mPlc2 ≅ 2×109J ≅ 1,2×1019GeV ca. 18 ordini di grandezza (un miliardo di miliardi di volte) più elevata di quelle attualmente esplorate negli acceleratori, e una lunghezza di Planck,
inferiore di circa 20 ordini di grandezza rispetto alle dimensioni di un nucleo di idrogeno. Il ruolo di queste quantità è oggi in gran parte misterioso. Semplici argomenti dimensionali sono però in grado di evidenziarne diverse possibili manifestazioni, tra loro collegate, quantomeno nell’ipotesi, alquanto suggestiva sebbene non ineludibile, che le indicazioni della relatività generale siano estrapolabili fino ad altissime energie. Per es., confrontando le leggi di Newton e di Coulomb per una coppia di particelle statiche e puntiformi di carica elettrica pari alla carica e dell’elettrone e massa m, rispettivamente
è naturale associare alla gravità un analogo della costante di struttura fine che caratterizza le interazioni elettromagnetiche,
Il valore piuttosto esiguo di α è alla base della relativa semplicità delle interazioni elettromagnetiche. La sua controparte per la gravitazione, ottenuta collegando formalmente massa ed energia mediante la relazione di Einstein
,
è una funzione crescente dell’energia. Le interazioni gravitazionali tra elettroni descritte dalla relatività generale, per es., assai più flebili di quelle elettromagnetiche in condizioni ordinarie, diverrebbero così ben più intense a energie dell’ordine di EPl. Questa enorme crescita di intensità è anche all’origine di alcune spinose difficoltà matematiche, perché rende le correzioni quantistiche in gravità praticamente fuori controllo. Considerazioni simili evidenziano un profondo legame tra lunghezza di Planck e fisica dei buchi neri. Un buco nero macroscopico è un corpo il cui intenso campo gravitazionale preclude a osservazioni da grande distanza la regione racchiusa dal suo orizzonte degli eventi. Questa superficie ideale dista dal suo centro per il cosiddetto raggio di Schwarzschild, espresso dalle
Per una massa M≅2×1030 kg, pari a quella del Sole, il suo valore è ca. 3 km. Se ora potessimo ridurre M, la corrispondente lunghezza d’onda Compton crescerebbe mentre il raggio di Schwarzschild diminuirebbe; per un buco nero di massa pari a mPl entrambe verrebbero essenzialmente a coincidere con la lunghezza di Planck lPl in virtù della relazione
che segue dall’espressione della massa di Planck. In base alle precedenti considerazioni, particelle con energia EPl sarebbero naturalmente in grado di produrre buchi neri microscopici di questo tipo, rendendo problematica la natura stessa dello spazio-tempo a scale di distanza confrontabili con la lunghezza di Planck lPl.