Scienza greco-romana. La matematica nel V secolo
Scienza greco-romana. La matematica nel V secolo
La matematica nel V secolo
Il titolo di questo capitolo è di per sé problematico. Decidere se al di là di alcuni lavori isolati si possa parlare di ‘matematica’ nel V sec. a.C. è infatti un vero e proprio problema storico. Le testimonianze si riducono ad alcune citazioni indirette e a un solo lavoro di una certa lunghezza, in una copia che per di più risale al VI sec. d.C. (ne parleremo diffusamente più avanti). Non si può nemmeno cercare di colmare il vuoto gettando un ponte tra quanto sappiamo della matematica precedente e quella più tarda, perché non esiste alcuna matematica greca precedente. Siamo così di fronte al problema delle ‘origini’ e a quello della ‘definizione’; occorre delimitare la matematica cronologicamente e concettualmente, nelle sue interazioni con le altre discipline. Solamente dopo aver esaminato questi aspetti di carattere principalmente metodologico si può cercare di cogliere dalle testimonianze il contenuto della matematica di questo periodo e spiegare il significato che questa matematica può aver avuto per gli autori e per il pubblico dei lettori.
Il problema delle origini
Erodoto, che scrive nella metà del V sec., è il più antico degli autori a noi pervenuti che si occupa delle origini di una ‘matematica greca’, riferendosi soprattutto alla geometria. Egli afferma che le sue origini si trovano in Egitto e a Babilonia, e inoltre attribuisce a Talete, il saggio di Mileto, la predizione di un’eclissi. Il quadro che viene fornito è quello di una tradizione del Vicino Oriente portata in Grecia da saggi come Talete (attivo agli inizi del VI sec.). Sono questi i due temi che devono essere affrontati: il Vicino Oriente antico e i personaggi che hanno fondato la filosofia greca, non soltanto Talete, ma naturalmente anche Pitagora (attivo nel VI sec., e che Erodoto non nomina specificamente come scienziato). Invertendo l’ordine cronologico, discuteremo prima il ruolo dei saggi delle origini; ciò ci porterà a considerare il legame fra le origini greche e la matematica del Vicino Oriente antico.
I saggi del primo periodo
Per comprendere la tradizione relativa ai primi saggi, come Pitagora, nel tentativo di rintracciare le origini della matematica del V sec., è necessario considerare il modo in cui essi vennero compresi e utilizzati da coloro che costituiscono le nostre fonti, e cioè autori più tardi, da Platone in poi. Non vi sono alternative convincenti a questa metodologia, adoperata da Walter Burkert (1962), il quale è molto scettico riguardo al fatto di considerare Pitagora uno scienziato. Anche se alcuni studiosi (da ultimo, Zhmudà 1997) respingono le affermazioni di Burkert, i suoi interrogativi non si possono ignorare.
La matematica attribuita ad autori come Talete e Pitagora è di tipo molto elementare, in genere del livello del Libro I degli Elementi di Euclide. Occorre tener conto, però, del fatto che molte delle attribuzioni risalgono al commento a questo libro scritto da Proclo nel V sec. d.C. Per esempio, si attribuisce a Talete la dimostrazione del fatto che il cerchio è diviso dal diametro in due parti uguali e a Pitagora, ovviamente, il teorema di Pitagora. La verità è che queste attribuzioni non hanno un reale fondamento. Vi sono tre problemi, in ordine crescente di difficoltà.
Innanzi tutto, le fonti che attribuiscono risultati matematici precisi a personaggi delle origini sono molto tarde; si tratta in genere di autori della Tarda Antichità (per lo più proprio Proclo), che in alcuni casi rinviano a fonti del IV sec. (nel migliore dei casi a Eudemo, delle cui storie delle discipline matematiche parleremo in seguito).
Tuttavia, la cronologia in sé è un fattore meno importante del fatto che le fonti tarde in nostro possesso provengono da un contesto molto diverso da quello degli autori di cui esse trattano. È il caso di Aristotele, la nostra fonte abituale per quanto riguarda i presocratici. Aristotele fu un autore molto prolifico. Il corpus originale che ci è pervenuto – soltanto una parte di quanto ha scritto – consta di circa un milione di parole; Platone, che ebbe grande influenza su di lui, di parole ne aveva scritte almeno mezzo milione. Una vita che faceva tutt’uno con la parola scritta, e anche, nel Liceo, una vita d’insegnamento. Quella dei saggi del VI sec. deve essere stata una vita molto diversa. Il ruolo della scrittura nella cultura greca non fu costante, ma subì cambiamenti sia nel tempo sia attraverso i diversi contesti culturali (Thomas 1992). In particolare tra il VI e il IV sec. il cambiamento fu molto drastico: è dubbio che Talete abbia mai scritto qualcosa ed è quasi certo che Pitagora non scrisse mai nulla. Si può essere scienziati e perfino matematici senza mai scrivere nulla, ma in questo caso la scienza prodotta rischia di essere modificata dal modo in cui è trasmessa, ed è probabile che un autore come Aristotele, che proviene da un contesto culturale in cui domina la scrittura, dia una rappresentazione di storta di un autore appartenente a una tradizione essenzialmente orale.
Comunque, questo secondo problema è ancora minore rispetto al terzo e ultimo che dobbiamo considerare. Non si tratta infatti solamente di una rappresentazione che senza volere è distorta, è fuor di dubbio che le figure del passato siano state deliberatamente manipolate. Già nel V sec. Pitagora e Talete non erano nomi neutri di antichi personaggi, ma avevano un contenuto simbolico. Aristofane usa il nome Talete in due commedie, le Nuvole e gli Uccelli, in entrambi i casi per indicare all’incirca ‘qualcuno che vuol fare il furbo’. In altre parole, ‘Talete’, era un ‘segno’, non un ‘significato’. Dicendo Talete, Aristofane vuole chiarire il proprio punto di vista sui sofisti di un certo tipo, suoi contemporanei. Allo stesso modo Aristotele parla dei pitagorici principalmente quando vuole mettere in evidenza un punto in cui Platone sbagliava, mentre più tardi Pitagora divenne invece il simbolo della matematica di tipo platonico.
In conclusione, quando dal V sec. guardiamo all’indietro al VI, ciò che vediamo sono in realtà le ombre che su questo hanno gettano i secoli più tardi. Ma se non ci sono testimonianze dirette è perché i saggi dell’epoca hanno scritto molto poco. Quando lo hanno fatto, l’interesse per questi primissimi lavori è stato tale che, malgrado tutte le difficoltà, tracce consistenti lasciate dai loro scritti sono giunte fino a noi (per es., sappiamo di Eraclito molto più di quanto non sappiamo di numerosi autori ellenistici). I saggi s’interessarono di matematica? Forse, ma in tal caso non ne scrissero probabilmente mai, e quindi non doveva trattarsi di una matematica molto diversa da quella della tradizione orale prescientifica dei praticanti diffusa in tutto il Mediterraneo orientale. Il problema delle origini greche si collega così a quello delle origini non greche. Prima di passare ad analizzare queste ultime vogliamo sottolineare quanto abbiamo appreso fin qui; non si tratta solamente di sapere chi furono i primi matematici greci, ma anche chi furono i primi ‘autori’ matematici greci; è un problema questo che riguarda l’uso della scrittura, che nel corso del V sec. subì una profonda trasformazione.
Il Vicino Oriente antico
La nostra comprensione di una cultura del passato è in generale sempre condizionata, assieme alle vicende spesso casuali della sua sopravvivenza, dai modi di scrittura dei quali ha fatto uso. Le tavolette di argilla in Mesopotamia e i papiri in Egitto si sono mantenuti nel tempo anche grazie al clima e poiché si tratta dei mezzi più usati per la scrittura quotidiana nel Vicino Oriente antico siamo in possesso di una visione più unica che rara della pratica della scrittura in queste culture. In alcuni casi ci restano infatti non soltanto campioni, ma qualcosa che si avvicina molto al totale di quanto è stato scritto in un dato luogo e in una data epoca: possiamo perciò fare generalizzazioni attendibili. Malgrado ciò che afferma Erodoto, l’Egitto non ha dato contributi significativi alla matematica greca; alcune tavolette di argilla della Mesopotamia mostrano invece una pratica matematica che a suo modo è molto sofisticata. Il grande studioso Otto Neugebauer ha proposto questa matematica babilonese come fonte diretta della prima matematica greca; un’ipotesi avanzata a titolo provvisorio e che, pur credibile, si è affermata soprattutto grazie al prestigio di Neugebauer. In realtà, è molto difficile esprimere in un senso o nell’altro un giudizio su questo problema, ma è chiaro che il quadro della matematica greca del V sec. cambia a seconda che la si consideri o no come uno sviluppo della matematica babilonese. A questo proposito vi sono almeno due problemi da affrontare, tra loro indipendenti. In primo luogo, esiste una qualche continuità concettuale tra la matematica babilonese e quella greca che avvalorerebbe l’ipotesi dell’origine babilonese della matematica greca? In secondo luogo, c’è una qualche forma credibile di contatto che possa spiegare una tale influenza?
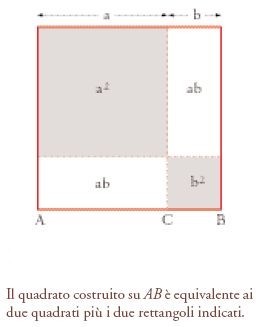
Neugebauer vede una continuità possibile in un campo che è stato chiamato ‘algebra geometrica’. Questa denominazione nasce dal fatto che, da un punto di vista moderno, è facile stabilire un certo isomorfismo tra alcune relazioni algebriche e geometriche elementari. Per esempio, l’uguaglianza (a+b)2=a2+2ab+b2 corrisponde al fatto geometrico che il quadrato costruito su un segmento AB è equivalente ai due quadrati costruiti sui due segmenti AC e CB, dove C è un punto tra A e B, più i due rettangoli che hanno per lati questi due segmenti (fig. 2). Il Libro II degli Elementi di Euclide contiene teoremi geometrici che riguardano uguaglianze tra aree di questo tipo; questo modo caratteristico dei Greci di trattare equazioni essenzialmente algebriche è stato definito ‘algebra geometrica’ (seguendo Zeuthen 1886). Molte tavolette babilonesi contengono istruzioni per risolvere problemi che si possono considerare equivalenti a questo genere di equazioni algebriche; si poteva perciò dedurre che una certa concezione teorica babilonese riguardante equazioni elementari fosse stata fatta propria da praticanti greci che le avevano dato un’interpretazione geometrica.
Tuttavia, recentemente questo approccio è stato rifiutato (Unguru 1975, 1979). Vi sono difficoltà storiografiche di fondo riguardo al problema del significato storico di un isomorfismo matematico. Qualunque cosa si possa dire delle strutture puramente matematiche, è evidente che i Greci attribuivano a un teorema geometrico un significato geometrico e non algebrico. Per i nostri scopi più immediati questo isomorfismo va considerato in relazione ad aspetti strutturali generali e non a risultati particolari, e per questa ragione esso si spiega meglio come risultato di sviluppi analoghi e non di influenze dirette. In altre parole, se si fa un certo tipo di matematica elementare è facile arrivare a risultati di questo genere, ma il problema delle origini non è risolto. Recentemente si è sostenuto che la matematica babilonese ha scopi geometrici, al pari degli Elementi di Euclide, per cui l’algebra geometrica sarebbe essenzialmente un tipo particolare di geometria, una geometria della misura delle superfici per mezzo di un’analisi del genere ‘taglia e incolla’ (come nel caso del quadrato costruito su AB nella fig. 2, che è diviso in quattro parti). Non è quindi fuori luogo chiedersi se l’interesse per una geometria di questo tipo sia stato importato in Grecia dalla Mesopotamia.
Giungiamo così alla seconda domanda: esistono forme credibili di contatto? In altri termini, occorre far corrispondere a una relazione astratta fra concetti, relazioni che facciano intervenire lo spazio, il tempo e gli individui concreti. A prima vista non sembra una ricerca molto promettente. Gli scritti matematici babilonesi risalgono per la maggior parte al 2000, cioè più di un millennio prima di Omero, e sono iscrizioni cuneiformi e in accadico – una lingua molto lontana da quella greca – con caratteri sillabico-ideogrammatici impressi su un supporto, le tavolette di argilla, che probabilmente non raggiunse mai i lidi egei. Tuttavia, è possibile che nel V sec. vi fossero dei praticanti del Vicino Oriente in possesso di una tradizione orale molto antica. Costoro potrebbero aver avuto contatti con controparti greche e ciò spiegherebbe il passaggio di conoscenze. È un’ipotesi che non possiamo controllare, ma si tratta certamente di una possibilità. Un certo tipo di informazioni matematiche sopravvive in modo sorprendente alla trasmissione orale; alcuni problemi matematici, con i medesimi parametri numerici, riaffiorano in continuazione e si tratta con tutta evidenza di problemi che non sono stati tramandati per iscritto (Hoyrup 1987). La questione è ovviamente analoga a quella della trasmissione di tradizioni popolari e di forme artistiche tra culture diverse; nel caso specifico del passaggio tra Vicino Oriente e Grecia la questione è stata studiata a fondo. Non c’è unanimità tra gli studiosi a questo proposito, anche se è chiaro che una qualche trasmissione vi sia stata. La semplice nozione di ‘trasmissione’ non spiega nulla; una cultura non si limita a prendere elementi da altre culture, ma rielabora e reinterpreta. Per quanto riguarda la matematica, è chiaro che la Grecia del V sec. ha profondamente rielaborato la tradizione orale dei praticanti, da qualunque parte essi provenissero.
Le due strade che abbiamo intrapreso per affrontare il problema delle origini della matematica, ossia la tradizione della Grecia più antica e quella del Vicino Oriente, ci hanno condotto alla stessa conclusione: qualunque siano le origini di questo o quel ‘contenuto’ matematico, esso deve aver subìto trasformazioni radicali in contesti diversi fra loro. Di conseguenza, quel che si deve cercare non sono tanto le origini di ‘qualcosa di simile ai contenuti del Libro II degli Elementi di Euclide’, bensì le origini di ‘qualcosa di simile al Libro II degli Elementi di Euclide’, il che è tutt’altra cosa. Dobbiamo chiederci quand’è che fu messo per iscritto su un rotolo di papiro qualcosa di qualitativamente simile alla matematica greca.
Un personaggio di Epicarmo, autore comico di Siracusa attivo nella metà del V sec., parla di addizioni e sottrazioni di ciottoli (su un abaco), e di numeri pari e dispari ottenuti come risultato; chi usava l’abaco aveva perciò già sviluppato una terminologia che più tardi avrebbe avuto un grande significato teorico. Ci sono sempre state numerose conoscenze matematiche non scritte, e possiamo anche supporre che fosse noto, per esempio, che ‘la somma di due numeri dispari è un numero pari’. È possibile che Erodoto si riferisca a questo genere di conoscenze non scritte quando afferma che la geometria proviene dall’Egitto; in tal caso si tratta di qualcosa che è più un’abilità, una tecnica, che una scienza. La domanda è, allora, se al tempo di Erodoto o di Epicarmo ci sia mai stato qualcuno che abbia messo per iscritto su un rotolo di papiro che ‘la somma di due numeri dispari è un numero pari’. D’altra parte, è ragionevole anche chiedersi perché mai qualcuno avrebbe dovuto preoccuparsi di farlo. Chi avrebbe dovuto scrivere, e perché? Mettere per iscritto su papiro delle conoscenze matematiche significava inserire queste ultime nel quadro della scrittura, renderle partecipi di quella cultura scritta che nel V sec. si stava sviluppando impetuosamente. Per capire le origini della matematica greca occorre perciò determinare quale posto la matematica occupasse nella cultura greca del V sec., i suoi rapporti con altre discipline e la sua affermazione come disciplina autonoma.
La matematica come disciplina
I cosiddetti ‘matematici’ babilonesi tutto erano fuorché matematici. Erano scribi, contabili, membri di corporazioni professionali caratterizzate dall’uso della scrittura e dei sistemi di numeri. Alcuni membri di queste corporazioni si dilettavano con problemi riguardanti la loro professione; è per questa ragione che tra le tante tavolette contenenti rendiconti relativi al tempio e alla corona se ne trovano qua e là alcune che chiamiamo ‘tavolette matematiche’. Si tratta però di una nozione moderna che è applicata a un materiale antico; queste tavolette sono perciò ‘matematiche’, ma non nel senso contemporaneo. Il concetto di ‘matematico’ è greco, e anzi la creazione di questo concetto, che identifica la matematica come un’entità a sé stante, è uno dei più grandi contributi della cultura greca; nacque proprio nel V sec., o al più tardi all’inizio del IV, e perciò la sua nascita deve occupare un posto centrale nelle discussioni che riguardano la matematica di quel secolo. Poiché il processo attraverso il quale una disciplina acquista la propria identità avviene per opposizioni e analogie, ci occuperemo dapprima di una possibile opposizione, cioè dei rapporti tra matematica e filosofia, e in seguito descriveremo l’affermarsi di un’idea di affinità fra le diverse ‘scienze matematiche’.
Matematica e filosofia
Il problema dei rapporti tra matematica delle origini e filosofia è stato concepito classicamente solamente in termini di rapporto tra pitagorismo e matematica (Cornford 1922-23); tuttavia, con l’affermarsi dell’attuale diffuso scetticismo nei confronti di Pitagora questa impostazione è venuta meno. Un nuovo impulso alla discussione è stato dato da Árpád Szabó (1969), il quale si è concentrato invece sul ruolo di Parmenide e in generale della filosofia eleatica. Parmenide è un punto di partenza molto più sicuro di Pitagora, poiché egli – come Zenone, suo seguace (attivo nella prima metà del V sec.) – lasciò certamente degli scritti, e questi ebbero molta influenza nel V sec. (v. cap. VII). Secondo Szabó, la caratteristica che distingue la matematica greca è il ruolo della ‘dimostrazione’ (di un tipo particolare formulato per la prima volta nella cultura greca), del tutto assente nella matematica babilonese. In altri termini, i matematici greci non si basano su ‘ciò che sussiste in un caso particolare’, ma su ciò che deve seguire necessariamente da certe ipotesi. La matematica greca è quindi interamente non empirica, vale a dire che è indipendente da argomentazioni visive basate su particolari figure o simili; inoltre, in essa si fa uso della dimostrazione indiretta (la reductio), cioè l’affermazione ‘P è vera’ si dimostra supponendo che sia vera ‘non-P’ e dimostrando che ciò porta a una contraddizione. Per esempio, per dimostrare che due cerchi distinti s’intersecano in non più di due punti, si suppone che essi s’intersechino in più di due (Elementa, lib. III, prop. 10). Da questa nuova ipotesi segue una contraddizione (nel nostro esempio, che i due cerchi hanno lo stesso centro, cosa che è impossibile per altre ragioni). L’ipotesi fatta era dunque falsa, quindi due cerchi distinti non possono incontrarsi in più di due punti. P è dimostrata confutando ‘non-P’. Il ruolo della dimostrazione indiretta è legato alla natura non empirica della matematica greca, perché in una tale dimostrazione il punto di partenza non si può esaminare empiricamente in quanto è impossibile, vale a dire non esiste. Una matematica che fa appello all’argomentazione indiretta è necessariamente non empirica, e, viceversa, soltanto in una matematica non empirica un tale genere di argomento è proponibile.
Questi due aspetti, l’approccio non empirico e l’argomentazione indiretta, si ritrovano nella filosofia eleatica, che finisce col negare completamente il mondo empirico. La tecnica principale di questa filosofia consisteva nel considerare ipotesi di senso comune, come, per esempio, ‘il moto esiste’, e trarre conclusioni assurde, dimostrando quindi che ‘il moto non esiste’. L’interpretazione storica proposta da Szabó si può quindi riassumere nel modo seguente: la negazione del mondo empirico da parte degli eleati porta allo sviluppo di tecniche di argomentazione indiretta. Queste ultime sono riprese dai matematici greci, che creano così un nuovo tipo di matematica, non più empirica. Nel valutare questo punto di vista occorre innanzitutto tenere conto del fatto che esso non poggia sull’ipotesi, tra l’altro difficile da sostenere, che i matematici greci seguano l’impostazione filosofica della scuola eleatica. Szabó non ha bisogno di attribuire ai matematici dell’Antichità improbabili posizioni filosofiche, anche se sostiene che essi siano profondamente influenzati dagli sviluppi della filosofia.
Su quest’ultimo punto Szabó è stato criticato da Wilbur R. Knorr, il quale sostiene essenzialmente che i matematici non sono interessati alle difficoltà di natura filosofica; essi sono invece stimolati dalle difficoltà ‘matematiche’, e la matematica si sviluppa risolvendo problemi interni al proprio ambito, i quali danno a loro volta origine ad altri problemi. Il punto di vista di Knorr permette di spiegare l’origine di molti sviluppi della matematica, specialmente in periodi più tardi, tuttavia dà per scontato che già nel V sec. esistesse una distinzione tra matematica e filosofia; la teoria di Szabó presenta comunque altre difficoltà, più serie. Innanzi tutto, essa può non offrire una descrizione adeguata della pratica matematica greca. Come vedremo in seguito, la matematica greca non divenne mai interamente non empirica, poiché anche nella sua forma più matura si basava sulle figure. D’altro canto, non è detto che la tecnica dell’argomento indiretto, anche se utile, abbia avuto la centralità che Szabó le attribuisce, né che questa tecnica sia necessariamente in contrasto con un approccio empirico; per esempio, cosa dire di una dimostrazione per assurdo che giunge alla conclusione ottenendo qualcosa che ‘si vede’ essere assurdo? Questo è anzi il metodo più comunemente usato dai Greci.
La separazione della matematica dalla filosofia non è un dato, ma qualcosa che si è costruito storicamente; a questo proposito, Szabó ha portato l’attenzione su alcuni importanti contesti culturali. La caratteristica della matematica greca è quella di essere di natura argomentativa e questa caratteristica riflette aspetti più generali della cultura greca del tempo. La storia della matematica del V sec. si può vedere come la storia dell’affermarsi di un tipo particolare di argomentazione, in un contesto nel quale altre argomentazioni erano proposte e sottoposte a giudizio. I paradossi di Zenone si possono considerare emblematici di questo sviluppo: benché siano spesso messi in relazione con le moderne di - scussioni sui problemi dei fondamenti della matematica dello spazio e del tempo (Salmon 1970), è evidente che essi furono introdotti come argomenti dialettici a favore della negazione eleatica del punto di vista empirico. Aristotele, la nostra principale fonte su Zenone, fu il primo a riproporre questi paradossi in un linguaggio più matematico e a discuterne nel contesto di problemi di fondamenti a proposito della struttura dello spazio. Scrivendo nel IV sec., quando la matematica era già ben affermata come disciplina indipendente, Aristotele dunque trasformò i paradossi di Zenone presentandoli, tra l’altro, mediante figure. In questo modo la matematica influenzava non tanto la filosofia eleatica in sé, quanto piuttosto la sua percezione e la sua diffusione. Non è detto comunque che si possa parlare di ‘matematica’ alla metà del V sec., periodo in cui Zenone scriveva; gli argomenti matematici non avevano ancora assunto il ruolo paradigmatico che avranno per Platone e Aristotele. Quando e dove acquisirono questo ruolo?
La ‘fratellanza’ matematica
Su Filolao, filosofo del tardo V sec. a.C., abbiamo questa testimonianza: «Secondo Filolao la geometria è principio e madre [...] delle altre [scienze]» (DK 44 A 7a). Secondo una possibile interpretazione, questo frammento rivela che la matematica aveva già una propria identità e che era percepita come una comunità di scienze connesse tra loro; proprio come Corinto e la sua colonia Corcira (Corfù), l’astronomia o la musica erano intese come colonie che mantenevano ancora legami con la ‘madrepatria’ geometria.
Filolao era noto come ‘pitagorico’, un termine che non implica un rapporto diretto con il Pitagora storico, ma è piuttosto una comoda etichetta per indicare un certo tipo di saggi vissuti tra la fine del V e gli inizi del IV secolo. Una delle caratteristiche principali dei ‘pitagorici’ era l’atteggiamento nei confronti della matematica, alla quale essi assegnavano un ruolo paradigmatico. Se Filolao è forse il primo autore di questo gruppo, Archita, che fiorì a cavallo del secolo, è forse il più brillante. Oltre che un matematico notevole (v. cap. XVII, per la soluzione da lui data al problema di trovare due medi proporzionali), Archita fu un importante filosofo (ma anche in questo caso è difficile fare una distinzione). Di lui ci resta questo frammento programmatico: «Ottime conoscenze mi sembra che abbiano acquisito quelli che si sono dedicati alle matematiche […] sulla velocità degli astri e sul loro sorgere e sul loro tramontare, e inoltre sulla geometria e sull’aritmetica e sulla scienza delle sfere e soprattutto sulla musica; perché queste scienze sembrano essere sorelle» (DK 47 B 1). Ritorna qui l’idea di considerare le scienze matematiche come una comunità; si noti però che Archita sembra attribuire un ruolo preminente all’astronomia: se si tratta di una famiglia, si possono già intravedere dispute sulle priorità.
Filolao espresse quest’idea di comunità con una metafora di carattere politico, Archita quella della famiglia; entrambi si riferivano a qualcosa di simile alle moderne ‘scienze matematiche’. La locuzione ‘scienze matematiche’ è però fuorviante. Archita faceva riferimento a quelli che si sono dedicati ai mathḗmata, dove mathḗmata, plurale di máthēma, era solamente una forma nominale derivata dal verbo manthánō, che significa ‘imparare, studiare’. Questa è l’etimologia del nostro ‘matematica’ o ‘matematiche’, e per i Greci il termine non perse mai il collegamento con il suo significato primitivo; Archita si riferiva a ‘coloro che si occupano degli studi’. Quindi intorno al V sec. si riconosceva in ciò che noi chiamiamo ‘matematica’ una certa ‘somiglianza di famiglia’, e si riconosceva anche che essa godeva di uno status particolare. Si diceva semplicemente tà mathḗmata, ‘gli studi’, volendo significare un particolare e forse privilegiato tipo di studi. Inoltre, dalle testimonianze citate si possono trarre varie indicazioni per quanto riguarda la struttura interna di questa famiglia: Filolao dava priorità alla geometria, Archita, come detto, invece all’astronomia e alla musica.
Questa struttura concettuale è di fondamentale interesse storico, poiché costituisce il retroterra culturale della concezione platonica della matematica, così com’è esposta nel Libro VII della Repubblica, che più tardi doveva acquisire una posizione dominante nella riflessione occidentale sulla scienza e sull’istruzione. Platone non si limitò però a ripercorrere strade già aperte da altri. Cita, approvandola, l’idea di ‘comunità’ di Archita (ma senza nominarlo), prendendosi tuttavia la libertà di cambiare la gerarchia all’interno della famiglia mettendo per prima l’aritmetica e subordinando poi tutta la matematica alla dialettica e alla filosofia. Le tre fonti più antiche per l’idea di (scienze) matematiche ci forniscono perciò tre quadri differenti: Filolao metteva al primo posto la geometria, Archita l’astronomia e Platone l’aritmetica (ma in definitiva la filosofia). In breve, se i Greci di quel periodo riconoscevano l’esistenza di un certo campo chiamato matematica, e se le discipline che essi elencavano tra le scienze matematiche erano nel complesso sempre le stesse (aritmetica, geometria, musica, astronomia), non tutti ne concepivano allo stesso modo la struttura interna; è quindi presumibile che non ci fosse accordo sulla natura di questo campo di studi e su ciò che ne poteva determinare l’identità. Platone era interessato alla matematica perché la vedeva relativamente astratta e non empirica (questo è il modo di concepire la matematica implicito nell’interpretazione di Szabó) e per questa ragione metteva l’aritmetica per prima. Archita invece metteva per prime la musica e l’astronomia, considerando forse per quest’ultima dati astronomici concreti; la sua concezione della matematica era molto più empirica, più vicina probabilmente alla nostra idea di ‘scienze esatte’. In effetti il contributo di Archita alla geometria ha un carattere fisico e concreto, anche se da un punto di vista filosofico era forse più interessato alle relazioni cosmiche tra il tutto e la parte che le osservazioni astronomiche suggeriscono.
Dunque, la concezione generalmente accettata di un’unità delle scienze matematiche non si basava su una filosofia della matematica condivisa da tutti, e ciò nemmeno all’interno del ristretto gruppo dei pitagorici: Filolao, Archita e Platone.
Ci si può chiedere allora da dove provenisse quest’idea dell’unità. Se non si trattava di una teoria, forse era suggerita dalla pratica, dal constatare che le varie discussioni svolgentisi in questi ambiti erano affini nelle loro tecniche. Si può allora formulare l’ipotesi che questa affinità si sia formata nella seconda metà del V secolo. Una testimonianza linguistica mostra come in questo periodo si avvertisse un senso di unità della matematica (delle matematiche), ossia l’uso del termine mathḗmata e, più sorprendentemente, quello di ‘geometria’. Anche se pone l’accento sull’aritmetica, Platone parla spesso di ‘geometria’ nel senso di ‘matematica’, e lo stesso accade per altri autori del tempo. Si tratta di una conferma del punto di vista di Filolao fornita dalla lingua; la parola ‘geometria’ era un punto focale, che concentrava su di sé tutti i termini che denotavano le ‘scienze matematiche’. La fonte del frammento relativo a Filolao citato prima è Plutarco, il quale, in una discussione contenuta nelle Quaestiones conviviales, cerca di spiegare perché si attribuisce a Platone la frase «Dio geometrizza sempre». L’affermazione è apocrifa ma, come osserva Plutarco, in linea con lo spirito platonico. Che cosa significa? Plutarco dà diverse spiegazioni; la più convincente è quella che ricorda come la geometria fosse considerata un punto centrale, per esempio da Filolao. Possiamo concludere che il Greco che inventò l’espressione «Dio geometrizza sempre» attribuendola a Platone (come pure il Greco che inventò la celebre espressione apocrifa «che nessuno entri se non è geometra» ponendola all’ingresso immaginario dell’Accademia), non pensava alla geometria in senso stretto, ma alla geometria come metonimia della matematica in generale. Dagli scritti di Platone, come pure dalla testimonianza relativa a Filolao, sembra chiaro che la geometria ottenne questo status metonimico già alla fine del V secolo.
Tutto ciò ci aiuta a rispondere alla domanda più importante: che cosa ha permesso alla matematica di acquisire in quel periodo una propria identità? L’affermazione della sua identità disciplinare nel V sec. si può collegare al legame esistente fra matematica e filosofia, e invece di limitarsi a esaminare il ruolo dell’argomento indiretto nella filosofia eleatica è utile considerare il fenomeno più generale della ricerca dell’‘argomentazione persuasiva’ nella cultura greca classica (Lloyd 1990). Risiede qui, in definitiva, la differenza cruciale tra la matematica del Vicino Oriente e quella greca; quest’ultima si affermò all’interno di una cultura nella quale l’argomentazione persuasiva aveva un ruolo dominante. Se da un lato la matematica era legata ad altre forme di argomentazione, dall’altro lato se ne distaccava perché i suoi strumenti di persuasione erano di un nuovo genere. Quindi è un’ipotesi plausibile che l’identità acquisita dalle scienze matematiche verso la fine del V sec. rifletta il fatto che una volta messi per iscritto argomenti di un certo tipo (che possono essere qualificati come ‘matematici’) si rende evidente il suo potere di persuasione unico; si tratta invero di ‘dimostrazioni’. La famiglia matematica è dunque la famiglia della dimostrazione; poiché la geometria svolge il ruolo di punto focale per questa famiglia (ritroveremo spesso questa centralità nella matematica greca), è opportuno capire in cosa consista la particolarità delle ‘dimostrazioni geometriche’, e anche in che modo altri tipi di dimostrazione si siano formati attorno a esse.
Il contenuto della matematica
Della prima matematica greca ci è pervenuto ben poco. Alcune fonti non sono lontanissime cronologicamente (soprattutto Platone e Aristotele), ma i principali problemi trattati sono di natura filosofica e non propriamente matematica. Abbiamo una testimonianza molto importante su un grande matematico, Ippocrate di Chio (da non confondere con il medico Ippocrate di Coo), che risale però al VI sec. d.C., un millennio dopo il periodo in questione. Fortunatamente, grazie a essa possiamo intravedere qualcosa proprio sul fenomeno cruciale della dimostrazione geometrica; prenderemo in esame, quindi, i contenuti della matematica del V sec. a partire da quest’unica fonte per poi muovere verso altre aree, meno documentate.
Ippocrate di Chio
Ippocrate visse nella seconda metà del V sec. a.C. Circa un secolo dopo, nel secondo capitolo del Libro I della Fisica, Aristotele osservava che come il compito dello scienziato non è di confutare tutti gli errori, ma soltanto quelli relativi alla propria scienza, così il matematico doveva confutare soltanto gli errori nella matematica. Cinquecento anni dopo, verso la fine del II sec. d.C., Alessandro di Afrodisia scrisse un commento (andato perduto) alla Fisica e discutendo questo punto suggeriva che Aristotele si riferisse a un errore commesso da Ippocrate di Chio. Tre secoli dopo, nel VI sec. d.C., Simplicio scrisse un altro commento alla Fisica e per dimostrare che il suo era superiore a quello di Alessandro di Afrodisia sottolineava gli errori presenti nel commento di quest’ultimo. Per esempio, Simplicio sosteneva che Ippocrate non aveva commesso l’errore che Alessandro gli attribuiva e per dimostrarlo citava un lungo passo di un vecchissimo libro, una ‘storia della geometria’ scritta da un allievo di Aristotele, Eudemo di Rodi (fine IV sec. a.C.). Questa citazione ci è pervenuta; si tratta della sola citazione di una certa lunghezza che ci rimane della ‘storia’ di Eudemo, e costituisce la fonte principale della matematica greca del primo periodo. Il percorso tortuoso attraverso il quale ne veniamo a conoscenza è significativo (Lloyd 1987).
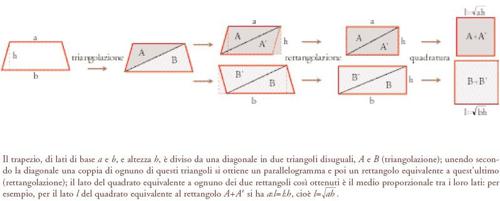
Il problema che è sullo sfondo di questo frammento è quello della quadratura del cerchio, vale a dire ottenere un quadrato avente la stessa area di un dato cerchio. ‘Quadrare’ una figura rettilinea è relativamente facile. Per esempio, si può cominciare col ‘triangolarla’, cioè ridurla a triangoli; ogni triangolo è considerato la metà di un parallelogramma, il quale è a sua volta equivalente a un rettangolo, e questo si può quadrare trovando il medio proporzionale dei lati (fig. 4). È probabile che questo genere di tecniche provengano dalla tradizione orale che ha preceduto la scienza greca del V sec.; esse costituiscono il tema principale dei primi due libri degli Elementi di Euclide. E il cerchio? Il cerchio non si può triangolare (Aristotele liquida così Brisone, un sofista che quadrò, sì, il cerchio, ma soltanto col rozzo metodo approssimato della triangolazione). Lo si può allora misurare in modo più o meno analogo a quello delle altre figure? Si può sezionare e manipolare in modo da farne una grandezza rettilinea? Se una figura complicata si può trasformare via via in un quadrato, perché la stessa cosa non si può fare per un cerchio? Non sappiamo come fu formulato per la prima volta questo problema, ma nella prima comparsa della matematica sulla scena della letteratura (e si tratta proprio di scena, alla lettera, perché avviene nelle commedie di Aristofane) un personaggio parla proprio della quadratura del cerchio come di un enigma.
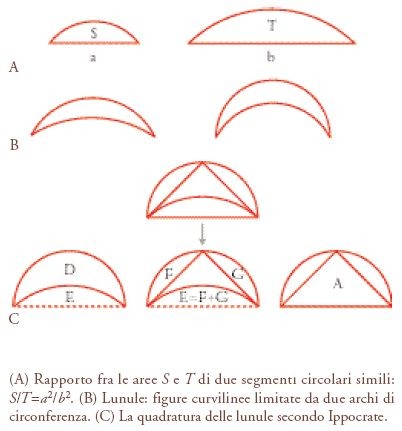
Supponiamo ora di sapere che i rapporti delle aree di superfici simili sono ‘il quadrato’ dei rispettivi lati (per esempio, se i lati di due quadrati stanno nel rapporto di 1 a 2, le loro aree stanno nel rapporto di 1 a 4), e supponiamo che ciò si possa generalizzare alle aree di figure curvilinee: per esempio, se due segmenti circolari sono simili, le loro aree stanno tra loro come i quadrati delle lunghezze dei segmenti che li delimitano (o, in modo equivalente, come i quadrati costruiti sui diametri di cui essi sono segmenti: fig. 5A). Anche quest’ipotesi può essere dovuta alla tradizione orale e, sorprendentemente, con essa una certa figura curvilinea si può quadrare. Ippocrate si occupò delle lunule, figure limitate da due archi di circonferenza (fig. 5B). Simplicio, che riporta la citazione di Ippocrate fatta da Eudemo, comincia così (fig. 5C):
Anche le quadrature delle lunule, che sembrano appartenere a un gruppo singolare di proposizioni in ragione della stretta relazione con il cerchio, furono dimostrate per la prima volta da Ippocrate, e sembra anche che sia stata stabilita correttamente da lui stesso. Ne parleremo quindi a lungo. Egli prese come punto di partenza, e come primo risultato utile per la quadratura, che segmenti circolari simili stanno tra loro come i quadrati delle loro basi. Questo lo dimostrò poggiandosi su quanto aveva dimostrato sulla costanza del rapporto dei cerchi ai quadrati dei loro diametri. Avendo dimostrato ciò, spiegò poi con quale metodo è possibile la quadratura di una lunula che ha una semicirconferenza come arco esterno. E fece ciò circoscrivendo un semicerchio a un triangolo rettangolo isoscele e [costruendo] un segmento circolare sulla base di questo, simile a quelli ritagliati dagli altri due lati. E poiché il segmento sulla base è uguale alla somma [dei segmenti] sugli altri [due lati], la lunula sarà uguale al triangolo. Pertanto la lunula, essendo uguale al triangolo, si può quadrare. In tal modo, prendendo come arco esterno della lunula una semicirconferenza, egli quadrò subito la lunula. (Diels 1903, 60.22-68.32)
Eudemo descrive nel seguito altri tre tipi di grandezze curvilinee che Ippocrate ‘quadrò’ in modo analogo (trasformò cioè in grandezze rettilinee). Il principio è sempre lo stesso, anche se la complessità è crescente. Ci troviamo di fronte a un’applicazione ingegnosa del metodo ‘taglia e incolla’, basato su principî molto elementari e su una brillante intuizione. Che Ippocrate fosse un genio è chiaro. Cos’altro si può dire di lui? In primo luogo, che aveva fatto altre cose, com’è confermato da ulteriori testimonianze che lo riguardano, pur se non altrettanto precise. Da una delle fonti si potrebbe desumere che egli scrisse un intero libro di ‘elementi’, cioè una prima versione degli Elementi di Euclide; ma questo sembra poco plausibile, vista l’epoca molto antica in cui è vissuto. In secondo luogo, Ippocrate fece qualcosa di sorprendente; e questo non è solamente un lusinghiero giudizio di valore, ma un aspetto importante del suo lavoro di cui occorre tener conto. Non è un caso che la prima testimonianza che abbiamo della matematica greca riguardi una misurazione sorprendente, e perfino paradossale. Siamo di fronte a una cultura nella quale la comunicazione ‘scientifica’ è concentrata sul paradosso; Zenone infatti dimostra che l’ipotesi della possibilità del moto si può trasformare nel suo contrario, Ippocrate che una figura curvilinea si può trasformare in una rettilinea. In terzo luogo, Ippocrate ‘dimostrò’ tutto ciò. Certo, non siamo obbligati a prestare ascolto a Eudemo, che gli attribuisce una successione logica di dimostrazioni a partire da assiomi, come se Ippocrate avesse dato una dimostrazione formale del fatto che ‘segmenti simili di cerchio stanno tra loro come i quadrati delle loro basi’ (si tratta di un risultato complesso che molto probabilmente egli non dimostrò, assumendolo soltanto). Ma supponendo certi fatti, le quadrature seguono come una necessità logica; una necessità logica, però, soltanto fino a un certo punto, poiché non fa intervenire esclusivamente parole e concetti. La dimostrazione si avvale non solamente della relazione logica tra le tappe intermedie ma anche dell’osservazione di una figura; la necessità della conclusione segue dall’osservazione della figura.
Riassumendo, nella seconda metà del V sec. circolavano scritti nei quali risultati sorprendenti (come la quadratura delle lunule) erano dimostrati combinando un’argomentazione e una figura. Tuttavia, la nostra principale fonte per la matematica del V sec. ci è pervenuta per vie indirette, e ciò può significare che conosciamo solamente una parte della storia. Rivolgiamo ora la nostra attenzione ad altre, più oscure, parti di questa storia. Nella conclusione ritorneremo a Ippocrate e vedremo come il fatto che ci sia pervenuto in modo indiretto può insegnarci qualcosa sulla matematica greca del primo periodo.
Il V secolo: la matematica che non conosciamo
Abbiamo osservato come Ippocrate di Chio avesse fatto conoscere attraverso i suoi scritti un risultato sorprendente ed eccezionale, il fatto cioè che era in grado di uguagliare figure curvilinee e rettilinee, e abbiamo anche detto che i risultati matematici del primo periodo erano in generale di questa natura. Ma cosa significa ‘sorprendenti’ ed ‘eccezionali’? Si tratta naturalmente di un concetto relativo, come dice Aristotele:
È indispensabile, comunque, che l’acquisizione della sapienza sollevi, in un certo modo, a un punto di vista che è contrario a quello in cui noi ci trovavamo all’inizio delle nostre ricerche. Tutti, infatti, come dicevamo, cominciano col provar meraviglia che le cose siano in un determinato modo, come sono soliti comportarsi di fronte alle marionette o ai solstizi o all’incommensurabilità della diagonale (difatti a tutti [quelli che non ne abbiano ancora indagato il motivo] sembra un prodigio il fatto che una certa lunghezza non possa essere misurata neppure dall’unità minima); ma, come avviene nei suddetti casi allorché gli uomini li abbiano compresi, così anche noi dobbiamo approdare, alla fine, al punto di vista contrario, che è anche, secondo il proverbio, quello migliore: difatti per un uomo esperto di geometria la maggiore stranezza del mondo sarebbe la commensurabilità della diagonale rispetto al lato. (Metaphysica, I, 2, 983a)
Questo passo ci suggerisce il nucleo essenziale della storia della matematica greca ai suoi esordi; essa sarebbe iniziata con affermazioni sorprendenti che avrebbero colpito il lettore qualunque, per poi arrivare a sorprendere non più soltanto l’uomo istruito ma anche il matematico esperto. In questo secondo stadio, che è quello dell’epoca di Aristotele, la ‘matematica’ si può già considerare una scienza a sé stante, distinta dalla filosofia in quanto ha le proprie fonti di meraviglia, un suo proprio programma di ricerca. Le parole di Aristotele ci ricordano però qualcosa di molto più preciso, e cioè che la scoperta dell’incommensurabilità, a cui egli fa continuo riferimento, era considerata il risultato forse più notevole e cruciale della prima matematica greca. Molti studiosi moderni hanno interpretato la storia della matematica greca del primo periodo sulla base di questa ipotesi. Quando ancora si giudicava fondamentale il ruolo dei primi pitagorici, un’idea centrale della storiografia era quella della ‘crisi dei fondamenti’. In breve, si pensava che fino alla scoperta dell’incommensurabilità la matematica greca fosse fortemente aritmetizzata, dove per aritmetica si intendeva la ‘teoria degli interi’ (ci si basava sul ruolo dell’aritmetica così intesa nel pensiero tardopitagorico). Con la scoperta dell’incommensurabilità non era più possibile descrivere tutti i rapporti tra oggetti come rapporti tra interi (per es., il rapporto tra due interi non può mai essere uguale al rapporto tra la diagonale e il lato di un quadrato); di qui la necessità di trovare ‘nuovi fondamenti’. La matematica fu allora geometrizzata e trovò infine una fondazione rigorosa nella teoria delle proporzioni di Eudosso, una teoria non più aritmetica.
Questa impostazione è oggi rifiutata, non soltanto perché ha come punto di partenza i pitagorici, ma perché non vi sono elementi che possano far pensare a una crisi come quella ipotizzata nella prima matematica greca. D’altra parte, è quanto ci si doveva aspettare; infatti, un fatto strano e sorprendente non era per i Greci fonte di perplessità, bensì di meraviglia, non un ostacolo per la scienza ma, al contrario, un motore dello sviluppo scientifico. La scoperta dell’incommensurabilità non portava a una crisi dei fondamenti, ma, al contrario, rendeva la matematica più interessante per i non specialisti.
Di conseguenza, la questione centrale non riguarda tanto le ripercussioni che può aver avuto all’epoca una crisi dei fondamenti, quanto il modo in cui i Greci hanno scoperto l’incommensurabilità. L’unico riscontro diretto lo abbiamo negli Elementi di Euclide, un’opera molto più tarda. Il Libro X tratta del fenomeno dell’incommensurabilità in modo molto particolareggiato, ma una sola proposizione ne dimostra l’esistenza. Si tratta precisamente dell’ultima proposizione del libro (prop. 115), che riguarda il risultato di cui parla Aristotele nel passo sopra citato: il lato e la diagonale del quadrato sono incommensurabili. Numerosi studiosi considerano oggi questa proposizione come un’aggiunta tarda agli Elementi, e in ogni caso essa è marginale nel progetto di Euclide; la meraviglia matematica è emigrata altrove. Non è detto quindi che la dimostrazione euclidea dell’esistenza dell’incommensurabilità sia quella originale. Ma qual è allora la dimostrazione originale? E come sono nate le varie dimostrazioni?
È stato suggerito che la scoperta dell’incommensurabilità sia stata innanzi tutto la scoperta di un’‘antiaferesi’ infinita, cioè di una ‘sottrazione reciproca’ che va avanti all’infinito. Quella della sottrazione reciproca è una tecnica fondamentale e la sua particolarizzazione ‘all’infinito’ (Tav. I) potrebbe essere il modo che ha permesso di scoprire l’incommensurabilità della diagonale e del lato del quadrato. Knorr (1975) è critico verso questa interpretazione e ha suggerito un’altra via, più vicina a quanto si trova nella proposizione citata degli Elementi di Euclide. L’incommensurabilità può essere stata trovata con un argomento indiretto, supponendo cioè la commensurabilità e arrivando a un risultato del tipo ‘uno stesso numero è pari e dispari’. Risultati di questo genere si possono ottenere non solamente supponendo che la diagonale e il lato del quadrato siano commensurabili, ma anche con altre ipotesi basate su proprietà e relazioni fondamentali tra interi (il fatto di essere relativamente primi, pari o dispari, ecc.). Un’analisi di questo tipo implica un punto di vista sulla matematica greca delle origini diverso da quello che si trova nella testimonianza su Ippocrate. Secondo Knorr quella matematica non era strettamente di tipo geometrico, ma anzi poggiava fortemente su quella che possiamo chiamare teoria dei numeri.
La sottrazione reciproca potrebbe essere stato uno degli interessi principali dei primi matematici. Oltre alla possibilità di dar luogo geometricamente a sottrazioni reciproche che proseguono all’infinito, è stato sottolineato che a questo riguardo si apre un intero campo di ricerca: ogni sottrazione reciproca genera una successione di numeri interi; che cosa si può dire del rapporto tra queste successioni, e come si possono dedurre l’una dall’altra? (Fowler 1987). Infine, un’altra interpretazione possibile sulla matematica greca delle origini, ancora diversa da quella puramente geometrica di Ippocrate, è collegata ai molti riscontri di un interesse assai precoce per la matematica della musica. Sembra che già nel V sec. vi fosse una consapevolezza della stretta relazione tra le armonie musicali e alcuni rapporti numerici semplici (per es., il rapporto tra le lunghezze di due corde dello stesso tipo che emettono suoni che distano di un’ottava è di 1 a 2). Ciò può aver spinto allo studio dell’‘armonia’, ossia all’analisi dei vari tipi di rapporti numerici semplici e soddisfacenti (Barker 1989, vol. I).
Non possiamo pertanto imputare soltanto ai nostri limiti di carattere storico l’impossibilità di stabilire con certezza in che modo i Greci hanno studiato per la prima volta il fenomeno dell’incommensurabilità. Ci troviamo in realtà di fronte a diverse possibilità, e se alla fine del V sec. si stava affermando una certa unitarietà tra le diverse scienze matematiche, ciò non significa che vi fosse un’unica linea di ricerca; la questione del l’incommensurabilità poteva essere affrontata da punti di vista diversi. Il vero problema storico non è perciò quello del punto di vista dominante nel V sec., ma piuttosto quello del grado di unità raggiunto dalla matematica greca. Abbiamo rilevato come, nell’unica vera testimonianza di cui disponiamo, quella su Ippocrate di Chio, l’accento fosse posto su una geometria di tipo visivo, come pure il ruolo di risultati sorprendenti e di dimostrazioni rigorose. Abbiamo inoltre considerato vari suggerimenti riguardanti altri tipi possibili di matematica: un’analisi numerica della commensurabilità, uno studio delle proprietà della sottrazione reciproca e lo studio di rapporti musicali. Vi sono altre possibilità. Per esempio, su quale matematica poggiava l’astronomia del V sec.? Per alcuni storici (Bowen 1983) non si può parlare di matematica in astronomia, ma non vi è unanimità su questo punto. Se le possibilità sono tante, i riscontri sono troppo scarsi per poter dare risposte definitive. L’aspetto più importante è tuttavia proprio la varietà. Ci si può chiedere allora per quale ragione questa varietà non si rifletta nelle fonti. Perché le fonti del IV sec. ci presentano una matematica nella quale la sottrazione reciproca non è considerata? Come abbiamo visto, se la matematica del V sec. aveva già una propria identità, questa identità poteva ancora essere oggetto di dibattito; per Platone sembra essere l’aritmetica a svolgere un ruolo centrale, per Archita la musica e l’astronomia sarebbero invece più importanti, e per Filolao (secondo un frammento che si può attribuire a lui) la geometria è la madre di tutte le altre discipline. Questo dibattito sembra aver perso molto del suo significato nel corso del IV sec.; la matematica non soltanto aveva raggiunto una sua identità, ma proprio l’identità che noi le attribuiamo oggi, diventando cioè principalmente geometrica. Perché ciò sia accaduto è un altro problema; ne parleremo nel seguito, a proposito della struttura degli Elementi di Euclide. Ci basti osservare qui che il ruolo centrale della geometria potrebbe essere una conseguenza del ruolo delle dimostrazioni fatte con l’aiuto di figure, la tecnica di dimostrazione più usata da Ippocrate di Chio in poi. Il fatto di avere a disposizione un tipo particolare di argomentazione, estremamente persuasivo e inconfutabile con la sua combinazione di figure e dimostrazioni, ha permesso alla matematica greca di svolgere un ruolo particolarmente significativo in una cultura per la quale dimostrazioni e argomentazioni erano tanto importanti.
Si spiega così perché le fonti più tarde, dal IV sec. in poi, abbiano conservato della matematica greca quanto rispondeva all’idea che ci si era fatta della matematica. La sottrazione reciproca, per esempio, era poco interessante perché non si basava su dimostrazioni e figure. Siamo di nuovo in presenza del fenomeno dal quale siamo partiti, e cioè che il nostro punto di vista sulla matematica greca delle origini è condizionato da quanto interessava gli autori dal IV sec. in poi. È questa in definitiva l’ironia della sorte toccata alla matematica greca. Il passo di Ippocrate di Chio del quale siamo in possesso proviene da una tradizione aristotelica per la quale l’interesse principale era proprio la definizione di ciò che poteva dirsi matematico. Il punto di partenza da cui muove questa tradizione è una nota di Aristotele, secondo cui il matematico deve confutare soltanto gli errori che riguardano la matematica. L’interesse di Aristotele, come quello di altri autori suoi contemporanei, era rivolto alla classificazione del sapere, alla costituzione delle diverse discipline e alla delimitazione dei rispettivi campi. Dato che le scienze matematiche avevano raggiunto una loro identità, era naturale che questi autori prendessero la matematica come paradigma, e nel costituirsi come disciplina per eccellenza la matematica, o almeno la sua immagine, subì una trasformazione. La matematica in quanto disciplina unica e unificata è dunque probabilmente un prodotto del IV sec., e anzi in un certo senso può addirittura essere un’invenzione di Platone e Aristotele. Se lo fu, si tratta di un’invenzione che ebbe successo; dal IV sec. in poi, infatti, ha sempre più senso parlare di ‘matematica greca’ come di qualcosa di ben definito, e studiarla indipendentemente dagli sviluppi di altri settori della cultura greca.
Bibliografia
Barker 1989: Greek musical writings, edited by Andrew Barker, Cambridge- New York, Cambridge University Press, 1984-1989, 2 v.
Boardman 1994: Boardman, John, The diffusion of classical art in antiquity, Princeton (N.J.), Princeton University Press, 1994.
Bowen 1983: Bowen, Alan C. - Goldstein, Bernard R., A new view of early Greek astronomy, “Isis”, 74, 1983, pp. 330-340.
Burkert 1962: Burkert, Walter, Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaus und Platon, Nürnberg, H. Carl, 1962 (trad. ingl.: Lore and science in ancient Pythagoreanism, Cambridge (Mass.), Harvard University Press, 1972).
– 1984: Burkert, Walter, Orientalisierende Epoche in der griechischen Religion und Literatur, Heidelberg, Winter, 1984 (trad. ingl.: The orientalizing revolution. Near Eastern influence on Greek culture in the early archaic age, Cambridge (Mass.), Harvard University Press, 1992).
Cornford 1922-23: Cornford, Francis Maurice, Mysticism and science in the pythagorean tradition, “Classical quarterly”, 16-17, 1922-1923, pp. 137-150, 1-12. Diels 1903: Die Fragmente der Vorsokratiker, griechisch und deutsch, hrsg. von Hermann Diels, Berlin, Weidmann, 1903 (6. ed.: hrsg. von Walther Kranz, Berlin, Weidmann, 1951, 3 v., spesso indicata come DK) (trad. it.: I Presocratici. Testimonianze e frammenti, trad. di Gabriele Giannantoni, Bari, Laterza, 1969, 2 v.).
Fowler 1987: Fowler, David H., The mathematics of Plato’s Academy. A new reconstruction, Oxford, Clarendon Press; New York, Oxford University Press, 1987.
Hoyrup 1987: Hoyrup, Jen, The formation of ‘Islamic Mathematics’: Sources and condition, “Filosofi og Videnskabsteori pe Roskilde Universitetscenter 3 raekke: Preprints og Reprints”, 1987, Nr. 1.
– 1990: Hoyrup, Jen, Algebra and naive geometry. An investigation of some basic aspects of old Babylonian mathematical thought, “Altorientalische Forschungen”, 17, 1990, pp. 27-69, 262-354.
Huffman 1993: Huffman, Carl A., Philolaus of Croton. Pythagorean and presocratic. A commentary on the fragments and testimonia with interpretive essays, Cambridge-New York, Cambridge University Press, 1993.
Knorr 1975: Knorr, Wilbur R., The evolution of the Euclidean elements. A study of the theory of incommensurable magnitudes and its significance for early Greek geometry, Dordrecht-Boston, D. Reidel Publ. Co., 1975.
– 1981: Knorr, Wilbur R., On the early history of axiomatics. The interaction of mathematics and philosophy in Greek antiquity, in: Theory change, ancient axiomatics, and Galileo’s methodology, edited by Jaakko Hintikka, David Gruender ed Evandro Agazzi, Dordrecht-Boston, D. Reidel Publ. Co.; Hingham (Mass.), Kluwer Boston, 1981.
– 1986: Knorr, Wilbur R., The ancient tradition of geometric problems, Boston, Birkhäuser, 1986. Lloyd 1987a: Lloyd, Geoffrey Ernest Richard, The alleged fallacy of Hippocrates of Chios, “Apeiron”, 1987, pp. 103-128.
– 1987b: Lloyd, Geoffrey Ernest Richard, The revolutions of wisdom. Studies in the claims and practice of ancient Greek science, Berkeley (Calif.), University of California Press, 1987.
– 1990: Lloyd, Geoffrey Ernest Richard, Demystifying mentalities, Cambridge- New York, Cambridge University Press, 1990.
Neugebauer 1951: Neugebauer, Otto, The exact sciences in antiquity, Copenhagen, E. Munksgaard, 1951 (2. ed.: Providence, Brown University Press, 1957) (trad. it: Le scienze esatte nell’antichità, Milano, Feltrinelli, 1974).
Pingree 1994: Pingree, David, The teaching of the Almagest in late antiquity, in: The sciences in Graeco-Roman society, edited by Timothy D. Barnes, Edmonton, Academic Printing and Publishing, 1994, pp. 75-98.
Salomon 1970: Zeno’s paradoxes, edited by Wesley Salomon, Indianapolis, Bobbs-Merrill, 1970.
Szabó 1969: Szabó, Árpád, Anfänge der griechischen Mathematik, München- Wien, Oldenbourg, 1969 (trad. ingl.: The beginnings of Greek mathematics, Dordrecht-Boston, D. Reidel, 1978).
Thomas 1992: Thomas, Rosalind, Literacy and orality in ancient Greece, Cambridge-New York, Cambridge University Press, 1992.
Unguru 1975: Unguru, Sabetai, On the need to rewrite the history of Greek Mathematics, “Archive for history of exact sciences”, 15, 1975, pp. 67-114.
– 1979: Unguru, Sabetai, History of ancient mathematics. Some reflections on the state of the art, “Isis”, 70, 1979, p. 55 e segg.
Zeuthen 1886: Zeuthen, Hieronymus George, Die Lehre von den Kegelschnitten im Altertum, Køpenhagen, Höst, 1886.
Zhmud’ 1997: Zhmud’, Leonid Iakovlevich, Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin, Akademie-Verlag, 1997.