Scienza greco-romana. La scienza del cielo nel periodo pretolemaico
Scienza greco-romana. La scienza del cielo nel periodo pretolemaico
La scienza del cielo nel periodo pretolemaico
I documenti superstiti della scienza del cielo tra il IV sec. a.C. e il tardo II sec. d.C., come dire tra l’età di Aristotele (384/383-322) e quella di Claudio Tolomeo (100 ca.-178 ca.), sono irregolarmente distribuiti e incompleti. Per interi secoli e vaste regioni del mondo antico, ellenistico e romano, non ci è pervenuta nessuna testimonianza diretta dell’esistenza di una teoria degli oggetti celesti, e i pochi dati di cui disponiamo non contengono elementi che ci consentano di individuarne con precisione l’autore o la data. Inoltre, negli ultimi decenni del XX sec. lo studio di questi documenti è giunto a un’impasse critica; infatti, oltre alle consuete divergenze interpretative, si è creata una profonda divisione nel modo di concepire la reale natura dell’antica scienza dei cieli e l’identità di coloro che la praticavano. Questa divisione va attentamente considerata se si vuole che gli studi futuri conservino intatta l’aspirazione a una comprensione del passato. Guardando alla disputa da un punto di vista sistematico piuttosto che storico, la questione, nei suoi tratti essenziali, può essere enunciata nel modo seguente: come comprendere e scrivere la storia dell’antica scienza dei cieli dal momento che le fonti su cui deve basarsi l’interpretazione sono prive di continuità e di coerenza? Per risolvere la questione, sono state proposte due diverse strategie: narrativa e documentaria.
La strategia storiografica narrativa e quella documentaria
La strategia narrativa (rappresentata dalle opere di Th. Heath, J.L.E. Dreyer e B. Farrington) deriva prevalentemente dal presupposto che agli storici spetti il compito di rendere intelligibili i documenti che ci sono pervenuti, attraverso la narrazione storica o la costruzione di analisi riconducibili a una narrazione storica.
Nella sua forma più estrema questa strategia tende all’elaborazione di una grande sintesi progressiva nella forma di una narrazione globale che, seguendo tematicamente le tracce della testimonianza più antica e collocando tutti gli elementi via via disponibili in una struttura coerente, giunga fino alla testimonianza più recente. Tuttavia, questa strategia è destinata in partenza all’insuccesso se non si individua in maniera precisa l’oggetto della ricerca e ciò che è essenziale alla sua definizione. In assenza di questi elementi, infatti, non è possibile tracciare le linee della narrazione storica, vale a dire individuare i punti di partenza, i punti intermedi e quelli conclusivi, come pure i temi unificanti che rendano coerenti le storie (e le analisi che a queste devono essere ricondotte). I documenti in nostro possesso sul periodo pretolemaico, però, non danno queste indicazioni, e gli storici che scelgono questa strategia sono stati obbligati a fare assegnamento su scritti molto più tardi, dai quali selezionare gli elementi necessari all’elaborazione delle loro ricostruzioni. Ciò ha comportato attingere soprattutto alle opere di tardi autori ellenici, in particolar modo Proclo di Costantinopoli (410-485) e Simplicio di Cilicia (VI sec.).
Gli esponenti della strategia narrativa ricavano dalla storia successiva la comprensione di cosa fosse la scienza del cielo nel periodo pretolemaico, come pure di ciò che ne ha determinato lo sviluppo. Per colmare le lacune documentali, fanno affidamento soprattutto su un certo gruppo di citazioni più tarde (brani citati, parafrasi, traduzioni e riferimenti) di opere antiche andate perdute.
Descrizioni così costruite, com’è ovvio, rischiano inevitabilmente di cadere nell’anacronismo. Inoltre, la fiducia riposta da questi storici nelle testimonianze più tarde non può essere considerata fondata: gli antichi erano imprecisi e infedeli nel citare le parole e i pensieri dei loro contemporanei e dei loro predecessori. I motivi di ciò vanno ricercati nella natura stessa della storiografia antica; il modo in cui gli autori antichi concepivano la storia intellettuale e come essa dovesse essere scritta è sostanzialmente diverso dal nostro.
La speranza in una storia globale che descriva la storia della scienza del cielo greco-latina da Aristotele a Tolomeo è destinata a rimanere delusa, semplicemente perché i testi che ci sono pervenuti non sono sufficienti a fondarla (con l’espressione ‘scienza del cielo greco-latina’, si deve intendere solamente quella scienza trattata nei documenti redatti in greco e in latino; gli aggettivi ‘ellenistico’ e ‘romano’ stanno invece a indicare i relativi contesti sociali e intellettuali). Fin quando gli storici che si richiamano alla strategia narrativa saranno costretti a derivare dalla storia più tarda la concezione della scienza del cielo e di quel che ne ha determinato lo sviluppo, essi saranno inevitabilmente portati a emarginare e a trascurare opere ed eventi più antichi di primaria importanza. Ciò è particolarmente vero per quanti fanno assegnamento sulla tradizione storiografica che deriva da Proclo e da Simplicio, il cui pensiero filosofico è in gran parte un’elaborazione e un commento delle opere di Platone (428/427-348/347) e di Aristotele, considerate come un tutto armonico. Così, per esempio, nelle opere di questi storici non si troveranno citazioni degne di nota dei Phaenomena di Arato di Soli (315 ca.-m. dopo il 240); eppure, dei circa sei documenti sulla scienza del cielo del III sec. giunti in nostro possesso, i Phaenomena (che dopo l’Iliade e l’Odissea di Omero erano l’opera più letta dell’Antichità) sono indiscutibilmente il testo più significativo. Inoltre, salvo qualche eccezione, gli storici che utilizzano la strategia narrativa generalmente trascurano l’influenza esercitata dalla scienza del cielo mesopotamica sulla storia di quella ellenica e romana, soprattutto nel periodo in esame.
Ogni interpretazione storica tesa alla comprensione dell’antica scienza del cielo in un certo periodo deve essere verificabile in base ai documenti sopravvissuti che risalgono allo stesso periodo; altrimenti, si costruiscono schemi organizzativi sulla base di testimonianze più tarde e li si applica poi ab extra alle testimonianze del periodo pretolemaico. Il massimo che ci si può attendere da simili narrazioni è una lettura possibile di questi documenti, senza che si sia in grado di operare una scelta tra questa e altre letture possibili. Così non si produce conoscenza ma letteratura; la coerenza non s’identifica con la verità e il passato non ha l’obbligo di venire incontro alle nostre aspettative.
La seconda strategia, definibile come documentaria, è stata inaugurata da Neugebauer in diversi saggi scritti verso la metà del XX sec., e affonda le radici nell’opera di decifrazione di testi astronomici cuneiformi, molti dei quali costituiti da tavole numeriche. È una strategia basata sul principio secondo il quale lo scopo specifico della storia della scienza del cielo deve essere quello di spiegare i documenti pervenutici dall’Antichità punto per punto e nel miglior modo possibile, senza ricorrere all’apparato concettuale della strategia narrativa. Per uno storico che utilizza la strategia documentaria, l’oggetto di studio è principalmente di carattere matematico: dal suo punto di vista, infatti, devono essere spiegati l’argomentazione, la struttura, le tecniche e i parametri matematici contenuti nelle antiche opere sulla scienza del cielo sopravvissute.
Tuttavia, mentre non è possibile approfondire lo studio della scienza del cielo mesopotamica - gran parte della quale non soltanto è rappresentata da testi numerici e tabulari ma spesso non è accompagnata da alcuna spiegazione - senza concentrarsi sulla struttura matematica e sui suoi dettagli, le fonti relative alla scienza del cielo greco-latina hanno una diversa natura perché sono prevalentemente letterarie. Questi documenti, inoltre, contengono numerose definizioni e descrizioni di cosa sia l’astronomia che mal si conciliano con la definizione convenzionale prescelta dagli storici che adottano la strategia documentaria: molti autori antichi, greci e latini, del periodo pretolemaico semplicemente non avrebbero riconosciuto come propria tale definizione.
La strategia documentaria si rivela inefficace perché esclude dalla considerazione molti documenti che consentirebbero di comprendere il contesto sociale e intellettuale dei pochi trattati matematici greco-latini sulla scienza del cielo che ci sono pervenuti. Limitando arbitrariamente il campo dell’analisi si finisce con l’emarginare molti elementi utili per capire il modo in cui gli antichi autori greci e latini concepivano la loro scienza e come, nel corso del tempo, essi siano giunti a considerarla uno studio rigorosamente matematico dei fenomeni naturali.
All’origine del conflitto tra le due strategie sopra delineate e dell’impasse degli studi sulla scienza del cielo greco-latina sta il fatto che, nel corso del XX sec. e, soprattutto, nei suoi ultimi decenni, gli storici della scienza del cielo greco-latina hanno dovuto tener conto della pubblicazione di un corpus in continua crescita di testi mesopotamici. L’esame di questi documenti ha permesso di stabilire con certezza che, nel periodo che va da Aristotele a Tolomeo, la scienza del cielo mesopotamica ha avuto una significativa influenza sulle corrispondenti discipline elleniche e romane. Questa circostanza ha condotto alla scoperta di nuovi documenti relativi alla scienza del cielo greca e latina e alla riscoperta di documenti (e persino di brani) ignorati dagli storici della strategia narrativa, e ha portato gli studiosi a comprendere che l’astrologia è un argomento di importanza decisiva per l’interpretazione di un’evoluzione che ebbe il suo culmine nell’opera di Tolomeo.
Le nuove fonti hanno imposto agli storici un certo numero di scelte. In primo luogo, si è rivelato piuttosto difficile cercare di assimilare le nuove informazioni alle vecchie: i materiali greco-latini recentemente scoperti, che si richiamano prevalentemente a fonti mesopotamiche, sono infatti di carattere aritmetico e schematico, mentre quasi tutte le principali fonti tradizionali relative alla scienza del cielo greco-latina sono discorsive e di carattere geometrico o filosofico. Così, non è facile immaginare un modo di elaborare le consuete analisi narrative basate sui resoconti di Simplicio per assimilare correttamente testi come, per esempio, il papiro Hibeh 27: in questo documento, che risale al III sec. a.C., è contenuto uno schema aritmetico babilonese del tardo VIII sec. o dell’inizio del VII che serviva a determinare le variazioni delle ore di luce del giorno nel corso di un anno di 360 giorni, adattato all’anno egiziano di 365 giorni, in un calendario in cui sono segnalati i giorni nei quali certe stelle appaiono o scompaiono dalla volta celeste, e che indica non soltanto i più importanti eventi meteorologici ma anche i principali giorni in cui erano celebrate le feste e i riti del culto. Anche coloro che intenderebbero estendere l’applicazione della strategia documentaria, usata per interpretare i materiali mesopotamici, a tutti i documenti greco-latini sulla scienza del cielo, si trovano a dover affrontare lo stesso problema: oltre ai molti elementi filosofici contenuti in questi testi, quando gli autori greci e latini discutono teorie matematiche, le loro argomentazioni non sono esclusivamente aritmetiche ma prevalentemente qualitative e geometriche.
Se i tentativi di assimilazione falliscono e si rivela impossibile conservare o stabilire la coerenza, si può semplicemente decidere di ignorare il nuovo in favore del vecchio. Tra gli storici della strategia narrativa, questa decisione può presentarsi sotto la forma di una tesi, del genere di quelle sostenute da Farrington, secondo cui i materiali mesopotamici e i relativi testi greco-latini non mettono in discussione nessun aspetto significativo della storia della Natura e dell’origine della scienza del cielo greco-latina. In alternativa, si può scegliere di negare il vecchio in favore del nuovo; secondo gli storici della strategia documentaria, molti testi trattati dalla tradizione narrativa, come le osservazioni sull’astronomia e gli argomenti di carattere astronomico trattati da Platone e da Aristotele, sono irrilevanti o del tutto infondati. Tuttavia, poiché ognuna di queste posizioni esclude una parte dei documenti superstiti, si gettano dubbi sulla loro validità.
È possibile uscire da questa situazione di stallo? Il punto cruciale non è quello di risolvere la questione relativa al soggetto specifico di una storia della scienza del cielo greco-latina. Si tratta invece di reinventare il compito stesso di scrivere una tale storia, nel senso che è giunto il momento di considerare criticamente alcune questioni basilari relative al modo in cui gli studiosi definiscono e utilizzano le testimonianze nel corso delle loro ricerche.
Il profilo di una terza strategia
Il ripensamento critico dello studio della scienza del cielo greco-latina è un’operazione ancora in corso, per la quale i punti da tenere a mente sono almeno due. Il primo è mantenere il soggetto - la scienza del cielo greco-latina - come un vero e proprio tema d’indagine, evitando di darne una definizione preliminare. Le espressioni ‘scienza celeste’ e ‘scienza del cielo’, serviranno d’ora innanzi a designare qualsiasi cosa gli autori greci e latini di tutti i luoghi e di tutte le epoche del periodo che va da Aristotele a Tolomeo, ritenevano fosse il soggetto di questa scienza; comunque sembra che, tra questi autori, Tolomeo sia stato il primo a presentare un corpo di conoscenze sul cielo dotato della necessaria unitarietà sistematica e universalità. Il secondo punto importante è l’esigenza di produrre soltanto interpretazioni interamente verificabili sulla base dei documenti superstiti della scienza del cielo greco-latina e correggibili attraverso di essi.
Se vogliamo capire il modo in cui nell’Antichità gli Elleni e i Romani consideravano questa scienza, non ci resta che seguire la via più saggia e lasciare che la nostra comprensione dell’identità di questa scienza emerga gradualmente da uno studio approfondito dei suoi documenti. La comprensione che lo storico ha del soggetto si modifica, infatti, nel corso dell’indagine; è attraverso l’indagine e l’ulteriore esperienza così acquisita che giungiamo a riesaminare e ad arricchire la nostra conoscenza di determinati documenti e ad apprezzare nuove connessioni inizialmente trascurate. Così, chi affronta per la prima volta questi studi non capisce che cosa abbia a che fare la cucina con la storia della scienza del cielo greco-latina; nel corso dell’indagine egli potrà scoprire che l’arte culinaria aveva una grande importanza nell’antica medicina greca, come mezzo di prevenzione e di trattamento delle malattie, e che i medici ellenici del V e del IV sec. a.C. facevano assegnamento sulle credenze astrologiche popolari per scoprire la predisposizione alle malattie di una certa popolazione e le proprietà di diversi generi di nutrizione e di dieta.
Il nuovo approccio che si profila in questo modo rifiuta due affermazioni fondamentali relative alla scienza del cielo pretolemaica: che in essa esistesse una distinzione tra astronomia e astrologia (stabilita per la prima volta da Tolomeo); e che il suo vero oggetto di studio fosse costituito da una successione di teorie, di modelli e di tecniche, concernenti la rappresentazione dei moti celesti. Molti autori antichi greci e latini consideravano la storia della scienza del cielo come un elemento critico di un’impresa comune volta a ottenere dei benefici dagli dei o ad acquisire il maggiore numero possibile di nozioni sulla loro esistenza (cfr. Tolomeo, Almagesto, I, 1).
Rifiutandoci di definire preliminarmente il contenuto dello studio della scienza del cielo greco-latina, e in mancanza quindi di un riferimento a una precedente descrizione del suo soggetto, quali sono i criteri in base ai quali si devono selezionare e classificare i documenti appartenenti al suo corpus? La proposta storiografica è la seguente: ogni analisi storica della scienza del cielo greco-latina deve prendere in considerazione quesiti espliciti, accompagnati da una chiara spiegazione dei motivi della loro importanza, di ciò che presumono, e del modo in cui bisogna rispondervi. Si tratta, di conseguenza, di una strategia ‘interrogativa’; le domande dello storico e i loro relativi presupposti indicano, in ultima analisi, quali documenti devono essere considerati come prove. Per comprendere i documenti e i manufatti antichi attenendoci a ciò che essi esprimono, dobbiamo costantemente sforzarci di essere quanto più possibile consapevoli dei modi in cui la nostra inchiesta predetermina ciò che è scoperto e spiegato. Ma questa consapevolezza sarà raggiunta soltanto se le domande che suscitano e strutturano le nostre analisi sono sottoposte a una riflessione critica.
Naturalmente, a prescindere dalla strategia interpretativa adottata, tutti gli storici ritengono che i documenti corroborino le proprie analisi; ma è evidente che la natura o la qualità di questa convalida, i suoi limiti e il modo in cui è eseguita saranno diversi a seconda della strategia adottata. Per comprendere il genere di convalida di cui necessita la strategia interrogativa, si deve prendere in considerazione il problema di come oltrepassare l’interpretazione letterale dei documenti superstiti, di stabilire connessioni e di eseguire interpolazioni. La forma paradigmatica dell’interpolazione tra gli storici documentari è quella applicata al problema di stabilire se due testi incompleti di dati tabulari, numerici, riportati su tavolette d’argilla o fogli di papiro disgiunti siano originariamente appartenuti a uno stesso insieme. Se le parti si integrano effettivamente a vicenda, il problema è facilmente risolvibile in senso affermativo; ma se ciò non si verifica, ogni tentativo di ricostruire il contenuto delle tavolette o dei papiri deve basarsi su un’analisi matematica dei frammenti. Lo scopo dell’analisi è quello di stabilire se i valori numerici riportati dai frammenti si riferiscono a fasi successive di una stessa elaborazione matematica; così ogni parte mancante scoperta non soltanto renderà intelligibili i frammenti, ma sarà essenziale alla loro piena comprensione. Inoltre, la parte mancante interpolata sarà verificabile (per quanto possibile) attraverso l’esame dei frammenti e la dimostrazione dell’argomento matematico trattato.
Tuttavia, per quel che concerne i testi letterari, il problema è più complicato; le parole e i significati dei testi letterari solamente in alcuni rari casi richiedono di essere interpretati allo stesso modo dei numeri dei testi numerici. Il tipico problema della storia della scienza del cielo pretolemaica non è quello di stabilire connessioni tra differenti parti di un documento frammentario, ma quello di stabilire una connessione tra le parti di un documento che ci è pervenuto integro o quello di individuare le relazioni esistenti tra documenti diversi. Vale a dire che, abitualmente, il compito non è quello di dimostrare che due documenti appartenevano a un insieme più vasto, ma quello di scoprire la funzione di ciascuna parte in un determinato insieme, o il modo in cui un documento si rapporta a un altro.
Questo genere di dimostrabilità è differente da quello riscontrabile nelle consuete esposizioni narrative dedicate alla scienza del cielo pretolemaica. Queste ultime non soltanto stabiliscono connessioni tra documenti diversi in base a elementi estranei ai documenti stessi, ma talvolta, seguendo i loro schemi organizzativi, giungono persino a elaborare documenti andati perduti, della cui esistenza non vi sono prove se non un titolo riportato da qualche testo della Tarda Antichità o una breve citazione. Se si adotta la strategia interrogativa, la storia della scienza del cielo greco-latina diviene in primo luogo lo studio del corpus dei documenti letterari che ci sono pervenuti (papiri, iscrizioni, manoscritti, codici) e dei manufatti materiali (strumenti). Questi ultimi hanno un valore di prova inferiore ai documenti scritti, poiché molto spesso senza le testimonianze scritte non si può stabilire l’utilizzazione astronomica di questi strumenti e neppure il contesto sociale e intellettuale in cui sono stati fabbricati.
Ne segue che lo scopo principale degli storici è studiare il passato ma soltanto nel senso limitato di cercare d’interpretare una raccolta casuale di oggetti molto antichi disponibili. Per la strategia interrogativa questo corpus di testi e di strumenti costituisce la testimonianza concreta di un certo numero di attività correlate ed è anche l’unica base di qualsiasi tentativo di stabilire la natura di queste attività e delle loro interrelazioni. Lo stesso vale per i tentativi di ricostruire il pensiero o persino la mentalità degli autori e dei fabbricanti o degli utilizzatori di strumenti dell’Antichità, come pure il loro ambiente intellettuale e sociale: anche questi ultimi, infatti, sono descrivibili soltanto come ricostruzioni eseguite in base all’interrogazione dei documenti e dei manufatti antichi giunti in nostro possesso.
Il tentativo di fondare le interpretazioni dell’antica scienza del cielo sul materiale disponibile non deve basarsi per forza sull’idea che sia possibile descrivere il contenuto dei documenti facendo del tutto a meno della teoria; ciò, inoltre, è compatibile con la constatazione secondo cui la nostra conoscenza di questi contenuti come prove può presentare nel corso dell’indagine diversi gradi di contenuto teorico. Di conseguenza, un’indagine approfondita basata sulla strategia interrogativa non sempre potrà evitare che sorgano divergenze ben fondate tra gli interpreti. È evidente che il genere di verità che è stabilito raffrontando le interpretazioni al corpus dei documenti e dei manufatti astronomici che ci sono pervenuti varia a seconda delle domande formulate, delle tecniche impiegate per rispondere a queste domande e del modo in cui le spiegazioni che ne derivano sono sottoposte alla verifica. In altre parole, la strategia interrogativa non preclude l’effettiva possibilità di una disputa ben fondata e inconciliabile come caratteristica costante della ricerca storica. La verifica garantisce che le interpretazioni siano utilizzabili da tutti i membri della comunità degli storici e non soltanto da quelli che adottano un certo schema interpretativo; solamente se queste saranno interamente verificabili in base alle relative prove disponibili avranno un valore e un ruolo chiaro, ben definito, nell’evoluzione delle spiegazioni successive.
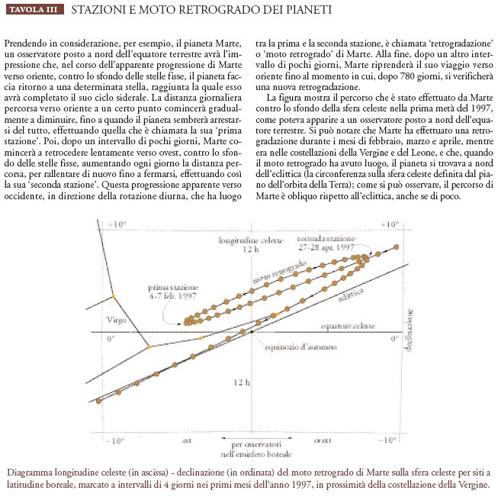
A partire dai presupposti metodologici enunciati finora, è utile affrontare tre domande concernenti la scienza del cielo così come è esposta nei testi greci e latini redatti tra il IV sec. a.C. e il II sec. d.C. La prima di queste è: quando, per la prima volta, gli autori greci e latini tentarono di spiegare i concetti di ‘stazione’ e di ‘retrogradazione’ planetaria, per esempio nel caso del pianeta Marte (Tav. III), e in che modo si proposero di produrre questa spiegazione? Un secondo quesito è il seguente: quando e come questi autori iniziarono a enunciare nei propri termini una teoria della scienza del cielo alla quale riconoscevano un’origine babilonese? E, infine: quando, perché e in quale contesto, gli autori greci e latini sostennero per la prima volta che la predizione, come pure la spiegazione, delle eclissi solari e lunari fosse una materia di competenza degli astronomi?
Lo studio dei fenomeni celesti prima del I sec. a.C.
Nel commentario al De caelo di Aristotele, Simplicio scrive:
come riferisce Eudemo nel secondo libro della sua Storia astronomica e come conferma Sosigene, che attinge a sua volta da Eudemo, si dice che Eudosso di Cnido sia stato il primo tra i Greci a mettere mano a questo genere di ipotesi, dopo che Platone, come afferma Sosigene, propose a quanti si occupavano con serietà di questi argomenti la seguente domanda: quali sono i movimenti uniformi e ordinati mediante la cui assunzione sia possibile salvare i fenomeni riguardanti i moti dei pianeti? (Simplicio, In Aristotelis De caelo commentaria, 488.18-24)
Questa osservazione è alla base della ricostruzione della storia della scienza del cielo greco-latina secondo la strategia narrativa.
Per Simplicio, il progetto di «salvare i fenomeni» comporta la spiegazione del moto di ciascun pianeta come un risultato apparente di un certo numero di movimenti che, in realtà, sono circolari e uniformi. Viene dunque naturale domandarsi quando abbia avuto inizio il progetto di spiegazione dei moti planetari secondo questo modello e quale spiegazione di tali fenomeni avrebbe potuto essere considerata valida. Simplicio riteneva, seguendo Sosigene (II sec. d.C.), che fosse stato Platone il primo a formulare il progetto di «salvare i fenomeni» planetari. Tuttavia, non esiste in tutti i dialoghi di Platone pervenutici un solo passaggio che esponga questo progetto, né vi è alcuna testimonianza diretta di esso negli scritti di Eudosso (attivo nella prima metà del IV sec. a.C.), Eudemo di Rodi (fine IV sec. a.C.) o Sosigene. In altre parole, non è possibile stabilire in nessun modo la veridicità delle affermazioni di Simplicio, il quale fa risalire il progetto alla fine del IV sec. a.C. Il resoconto di Simplicio non costituisce una base o un punto di partenza qualificato per la storia delle fasi iniziali della scienza del cielo greco-latina, ed è anzi sbagliato. Per dimostrarlo, è necessario innanzitutto esaminare le opere degli autori greci o latini del periodo compreso tra la fine del II sec. e l’inizio del I sec. a.C.: non vi è in esse alcuna prova valida della conoscenza dei fenomeni a cui allude Simplicio. In realtà, come si vedrà nel seguito, il progetto di salvare i fenomeni fu formulato nel periodo compreso tra il I sec. a.C. e il II sec. d.C.
Poiché i moti planetari presentano caratteristiche o ‘fasi’ diverse, è utile limitare l’analisi ai cinque pianeti allora conosciuti - Mercurio, Venere, Marte, Giove e Saturno - e alle più spettacolari fra queste fasi, cioè le ‘stazioni’ e le ‘retrogradazioni’. Di conseguenza, la domanda che si pone è: quando ebbe inizio, da parte degli autori greci e latini, il tentativo di fornire una spiegazione delle stazioni e delle retrogradazioni apparenti sulla volta celeste effettuate dai cinque pianeti e cosa è lecito affermare della strategia esplicativa adottata durante le primissime fasi di questo progetto?
A questo proposito, è importante distinguere tra i possibili modi di concepire i pianeti stessi: infatti, una cosa è supporre che i pianeti siano stelle erranti, e che alcune stelle - il Sole, la Luna e i cinque pianeti - non restino ferme nella stessa posizione rispetto alle altre, che sembrano rimanere fisse; altra cosa è pensare che tutte le stelle mobili siano lasciate indietro da quelle fisse e si muovano in una direzione opposta alla rotazione diurna della sfera celeste, o addirittura che il loro movimento (diretto e volto a oriente) sia un moto periodico. Infine, altra cosa ancora è supporre che alcuni pianeti - in particolare, Mercurio, Venere e il Sole - sembrino sorpassarsi reciprocamente, o estendere quest’idea anche a Marte, Giove e Saturno. In nessuno di questi casi, tuttavia, si può parlare di una consapevolezza delle retrogradazioni e delle stazioni dei cinque pianeti; e non vi è alcuna ragione valida per ritenere che gli autori greci o latini vissuti prima della fine del II sec. e dell’inizio del I sec. a.C. abbiano tentato di fornire una spiegazione delle retrogradazioni e delle stazioni dei pianeti. Infatti, prendendo in esame i brani più importanti addotti dagli studiosi della scuola narrativa a sostegno della tesi dell’esistenza di una consapevolezza di questo genere di moti in una data anteriore a quella che è fornita, e seguendo una strategia interrogativa, si renderà evidente che non esiste alcuna necessità, implicita negli stessi documenti, di una simile lettura.
Platone nel Timeo
Il progetto di «salvare i fenomeni» o le apparenze dei moti planetari sembra inconciliabile con l’epistemologia e l’ontologia presenti nei dialoghi platonici che affrontano il tema dell’astronomia, e in particolare la Repubblica e le Leggi. Sebbene in questi dialoghi venga mantenuta la distinzione tra il reale e l’apparente, se la celebre immagine della «linea divisa» nella Repubblica significa che gli oggetti del pensiero scientifico sono le Idee pure, costruite non come oggetti dell’indagine diretta ma come punti di partenza delle dimostrazioni che stabiliscono le effettive interrelazioni tra queste stesse Idee, allora non si può parlare di una ricerca della spiegazione scientifica di un fenomeno in quanto tale. In altri termini, i pianeti e i loro moti evidentemente non sono Idee o qualcosa di simile, e di conseguenza non è possibile averne una conoscenza scientifica; pertanto un programma che tenti di darne una spiegazione non può trovare posto nell’astronomia, dato che, almeno in questo dialogo, l’astronomia è considerata una scienza. Inoltre, il forestiero ateniese afferma nelle Leggi - contro quanti sostenevano che i pianeti non seguono mai lo stesso cammino e non manifestano quindi nessuna periodicità - che in realtà i pianeti non vagano, ma ciascuno di essi si muove costantemente lungo una sola orbita, bollando come blasfema l’usanza di chiamarli «stelle erranti». La sua tesi, secondo cui i pianeti possiedono un unico moto proprio, sebbene apparentemente sembrino seguire molti percorsi, è diretta contro coloro che negavano l’esistenza di qualsiasi ordine o regolarità nei moti planetari, per non parlare della conoscenza delle loro stazioni e retrogradazioni. Il forestiero ateniese, del resto, non distingue neppure il comportamento del Sole e della Luna, che non effettuano stazioni o retrogradazioni, da quello dei restanti pianeti, che, al contrario, le effettuano (Tav. IV). Ciononostante, esiste un brano in particolare, frequentemente citato dagli studiosi antichi e moderni, in cui si è creduto di scorgere un riferimento platonico alle retrogradazioni e ai moti diretti dei pianeti:
Ma le danze corali di questi astri, i loro incontri, rivoluzioni, progressioni (tàs tõn kýklōn pròs heautoùs epanakyklḗseis kaì prochōrḗseis seis), e quali, nelle loro congiunzioni e opposizioni, gli astri che si avvicinano e quali invece si trovano in opposta parte, e quali fra di essi passano gli uni davanti agli altri, coprendosi a vicenda, e in quali tempi si nascondono a noi, e in quali, invece, appaiono di nuovo, e spavento e segno mandano delle cose future agli uomini che nulla sanno di questi calcoli, tutto questo sarebbe fatica vana tentare di spiegarlo senza avere dinanzi agli occhi le loro immagini. (Platone, Timaeus, 40 c3-d3)
La tesi di questi studiosi è, in breve, che queste epanakyklḗseis e prochōrḗseis siano rispettivamente le retrogradazioni e i moti diretti dei pianeti.
Ora, verso la fine del IV sec. a.C. effettivamente era invalso l’uso di distinguere due generi di stelle: quelle che mantengono immutata la loro posizione reciproca e si muovono soltanto seguendo la rotazione diurna della sfera ce - leste, cioè le stelle fisse, e quelle che fisse non sono - il Sole, la Luna, Mercurio, Venere, Marte, Giove e Saturno - e che, oltre a effettuare la rotazione diurna, si muovono periodicamente in rapporto alle prime. Tuttavia, l’elemento caratterizzante di questa distinzione è che in essa non c’è traccia del tentativo di specificare - e neppure di nominare - i modi in cui le stelle erranti o i pianeti si muovono in rapporto alle stelle fisse. Inoltre, i pochi tentativi espliciti di individuare i moti osservabili dei pianeti si limitavano sostanzialmente ai loro moti siderali, cioè ai loro viaggi di ritorno lungo il circolo dello zodiaco fino a una certa stella o costellazione.
Così, Platone afferma nel Timeo che i sette pianeti si muovono lungo orbite circolari intorno alla Terra, poste tutte su un unico piano obliquo, in direzione opposta a quella della rotazione diurna. Dice, inoltre, che Mercurio e Venere, a differenza degli altri pianeti, nel corso del loro viaggio lungo quest’orbita obliqua sono superati dal Sole e lo superano a loro volta a intervalli regolari. Fin qui non sorgono problemi; ma le difficoltà nascono dall’affermazione di Timeo, il principale interlocutore del dialogo, che Mercurio e Venere sono raggiunti dal Sole e lo raggiungono a loro volta, nonostante si muovano lungo orbite dotate dello stesso periodo di quella solare, a causa di una forza o tendenza contraria a quella del Sole. L’affermazione di Timeo sui pianeti è stata addotta come prova del fatto che al tempo di Platone si era già a conoscenza dei moti retrogradi dei pianeti. Ma questa tendenza contraria comporta veramente un riferimento alla retrogradazione o una conoscenza di essa, oppure è possibile un’interpretazione più semplice, capace di cogliere il senso del brano senza ricorrere all’ipotesi di un riferimento alla retrogradazione planetaria?
Torniamo alla precedente descrizione di Timeo della costruzione dell’anima del mondo (v. cap. VIII). Il Demiurgo inizia modellando l’essenza dell’anima in una lunga fascia. Quindi, dopo averla suddivisa interamente in intervalli corrispondenti alla sequenza 1, 2, 3, 4, 8, 9, 7 e dopo aver inserito dei medi aritmetici e armonici e aver riempito gli intervalli nel rapporto di 4:3 con intervalli nel rapporto di 9:8, taglia la fascia per lungo in due strisce di uguale lunghezza, che sovrappone tra loro per formare una ‘X’, quindi ne unisce le rispettive estremità per produrre due circoli uguali, obliqui tra loro e congiunti in due punti diametralmente opposti.
Il Demiurgo […] le piegò per congiungerle in circolo, unendo fra di loro le estremità di ciascuna, nel punto opposto alla loro intersezione, v’impresse un movimento di rotazione nel medesimo spazio, e dei due circoli l’uno lo fece esterno, interno l’altro. Il movimento del circolo esterno lo destinò al movimento della natura del ‘medesimo’, quello del circolo interno al movimento della natura dell’‘altro’. Il movimento del ‘medesimo’ lo rivolse secondo la diagonale, da sinistra verso destra, quello dell’‘altro’, secondo la diagonale, da destra a sinistra. E dette la supremazia al movimento del ‘medesimo’ e del simile, e lo lasciò uno e indiviso, mentre sei volte divise il movimento interno, facendone sette circoli disuguali, secondo gl’intervalli del doppio e del triplo, sì che fossero tre per ciascuna parte. E a questi circoli ordinò che si muovessero in senso contrario gli uni agli altri, e volle che tre si muovessero alla stessa velocità, mentre gli altri quattro a velocità diverse l’uno rispetto all’altro e rispetto ai primi tre, ma tutti girassero sempre secondo un ritmo logico. (Platone, Timaeus, 36 c2-d7)
Timeo non specifica quali di questi moti planetari siano contrari a quali altri, né spiega in che modo si produca questa contrarietà od opposizione nella direzione del moto. Il problema è che il linguaggio da lui impiegato per descrivere la costruzione dell’anima del mondo è figurato, senza dubbio a causa della natura stessa del soggetto e del fatto che, a questo stadio della narrazione, l’anima del mondo non ha ancora un corpo e, di conseguenza, Timeo è costretto a parlare dei suoi moti senza riferirsi a ciò che si trova mosso o in movimento. Così, non è affatto sorprendente che ci si trovi in difficoltà quando si tenta di specificare con una certa attendibilità a cosa, in dettaglio, si riferisse Platone con questa costruzione. Tuttavia, un punto si può dare per assodato, ossia il fatto che, nella sequenza logica del racconto di Timeo, la divisione del moto o rivoluzione dell’‘altro’ in moti circolari, operata dal demiurgo, non produce di per sé moti che differiscano tra loro per la velocità o la direzione. Come si afferma chiaramente nel testo, questa differenziazione tra i moti o circoli in cui l’‘altro’ è suddiviso richiede un atto separato di prescrizione da parte del demiurgo. Ma, dato che l’anima del mondo non ha ancora un corpo ed è differenziata solamente dai suoi moti, quest’atto deve consistere nell’attribuzione di un moto supplementare ad alcuni dei moti planetari. In effetti, è possibile che il moto del Sole sia quello dell’‘altro’; che i moti del Sole, di Mercurio e di Venere siano dotati di una velocità analoga; che Marte, Giove e Saturno posseggano ciascuno un moto supplementare che si oppone costantemente alla rivoluzione dell’‘altro’, senza però vincerla; e che la Luna sia dotata invece di un moto supplementare che la favorisce.
Ma in che modo questa prescrizione si concretizza nell’edificazione del Cosmo? La risposta si articola in due parti. In primo luogo, sempre nel Timeo, il Demiurgo fabbrica il corpo di ciascun pianeta e lo colloca in una delle sette rivoluzioni che costituiscono il moto dell’‘altro’, in quello che potremmo definire un processo di formazione. Queste sette rivoluzioni non devono essere intese come sentieri o percorsi, bensì come semplici moti, ciascuno dei quali è una porzione dell’anima del mondo. Allo stesso tempo, queste rivoluzioni, che in origine erano semplici porzioni dell’anima del mondo, divengono l’anima di ciascun pianeta. Oltre a ciò, Timeo afferma che Mercurio e Venere sono dotati di poteri opposti a quelli del Sole, e questa opposizione si manifesta nel fatto che, rispetto al moto del Sole (che è costante e uniforme), ciascuno dei due pianeti può rallentare o accelerare la sua corsa verso oriente, anche se questi poteri sono esercitati in modo tale che i periodi delle loro orbite circolari verso est sono identici per tutti e tre gli oggetti celesti. In effetti Timeo assegna all’anima di Mercurio e di Venere un moto autonomo che aumenta o diminuisce in modo intermittente la rivoluzione dell’‘altro’.
Ma qual era lo scopo di Timeo? Si proponeva forse di spiegare il fatto che Venere e Mercurio non si allontanano mai troppo dal Sole e sono visibili soltanto per un breve intervallo subito dopo il tramonto o prima dell’alba, o era effettivamente a conoscenza delle loro stazioni e retrogradazioni? È evidente che l’osservazione che Venere e Mercurio sono stelle mattutine e serali, e quella che entrambe effettuano periodiche stazioni e retrogradazioni sono logicamente equivalenti. È ugualmente chiaro, tuttavia, che sarebbe errato dedurre dalla conoscenza della prima la consapevolezza dell’altra. Quale delle due, quindi, aveva in mente Timeo? Di fatto, le sue parole non offrono alcun sostegno all’ipotesi che egli si riferisse alle periodiche stazioni e retrogradazioni dei due pianeti. Bene o male, Timeo tenta di descrivere quelli che oggi chiamiamo i ‘moti reali’ di Venere e Mercurio e non i loro ‘moti apparenti’. Ora, la metafora utilizzata per descrivere il potere di ciascun pianeta di modificare il proprio moto verso oriente è quella di una gara su un percorso circolare: Mercurio e Venere sono immaginati come corridori che, pur riuscendo nel complesso a tenere il passo del Sole e a concludere la gara verso oriente nel suo stesso tempo, a volte rimangono indietro, ma successivamente recuperano il terreno perduto e superano il Sole, per poi rallentare ed essere a loro volta superati. Inoltre è importante sottolineare che in questa metafora non c’è nulla che implichi, richieda o presupponga il fatto che Mercurio e Venere effettuano stazioni e retrogradazioni in rapporto al firmamento. In altre parole, la rappresentazione di Timeo non implica l’esistenza delle stazioni e delle retrogradazioni di Mercurio e di Venere. Tutto ciò che la rappresentazione richiede è un’idea generale della direzione complessiva verso oriente della corsa; e questo a sua volta può ben essere stato inferito dal fatto che, generalmente, ogni giorno i pianeti sorgono sempre più tardi. In questo brano, quindi, non vi è alcuna ragione valida per supporre che Timeo fosse a conoscenza delle stazioni e delle retrogradazioni dei pianeti.
Questa conclusione rimanda ad altri brani del Timeo (40 c 3-d 3) e al problema di decidere cosa siano veramente le epanakyklḗseis e le prochōrḗseis di cui si parla. È certo che le epanakyklḗseis non sono altro che i moti circolari dei pianeti o il loro girare in tondo; infatti, la locuzione completa, «i ritorni dei circoli a sé stessi», è tipicamente pleonastica. Le prochōrḗseis, invece, stanno a indicare l’inarrestabile moto verso oriente, risultante dalla combinazione della rivoluzione dell’‘altro’ e del contributo specifico di ciascun pianeta a favore, o contro, questa rivoluzione. Non esiste, quindi, nessuna ragione cogente per distinguere nettamente tra una epanakýklēsis e una anakýklēsis e considerare la prima un moto contrario alla rivoluzione dell’‘altro’, anche se naturalmente è perfettamente lecito farlo. In ogni caso, nulla di quanto Timeo dice ci garantisce che egli si serva del termine epanakýklēsis per designare una retrogradazione; infatti, fino a quando non passa a discutere dei presagi planetari, le sue osservazioni si riferiscono sempre a tutti e sette i pianeti, senza nessuna specificazione o distinzione (e né il Sole né la Luna effettuano retrogradazioni).
Il sostantivo epanakýklēsis è raro; ricorre una sola volta nel corpus platonico e poi non è più documentato fino a un millennio più tardi, negli scritti dei commentatori platonici; non è facile quindi stabilire esattamente il suo significato nel Timeo. Il verbo corrispondente, epanakykleĩsthai, ricorre con una frequenza lievemente maggiore, ma soltanto una volta nel corpus platonico; è utilizzato con il significato di ‘girare in tondo’ in alcuni passi non databili degli scolî omerici, e il primo uso databile si trova in alcuni testi del II sec. d.C.: in genere, in questi e in altri documenti più tardi, il verbo significa ‘girare in tondo’, ‘ricorrere’, ‘ricorrere ciclicamente’, ‘muoversi in circolo’ e simili. Per tentare di chiarire il significato del sostantivo corrispondente, non resta quindi che indagare se il verbo sia utilizzato da Platone nella Repubblica per designare il moto retrogrado, o con qualche altro significato.
Durante la narrazione di quello che si è soliti chiamare il mito di Er, Socrate osserva:
il fuso tutto intero ruota su sé stesso con moto uniforme, ma durante il movimento circolare i sette cerchi interni lentamente girano in senso contrario a quello che è il movimento del tutto; fra i sette più rapido è l’ottavo [la Luna], vengono poi il settimo, il sesto, il quinto [il Sole, Venere e Mercurio]; a loro sembrava poi che terzo in velocità venisse il quarto [Mercurio], in questo inverso movimento rotatorio [epanakykloúmenon], quindi il terzo e infine il secondo [Giove e Saturno]. (Platone, Respublica, 617 a 4-b 3)
Ora, nessuno può dubitare che il moto di Marte descritto in questo brano sia un moto apparente e non un moto reale; analogamente, non possono esserci dubbi sul fatto che questo moto apparente non sia di tipo retrogrado, non sia cioè un moto verso occidente effettuato dal pianeta nell’intervallo tra due stazioni. Tenendo conto del meccanismo che governa i moti planetari, descritto nel mito di Er, può trattarsi solamente dell’inarrestabile moto verso oriente in direzione contraria alla rotazione diurna, moto che tuttavia Marte effettua con minore velocità rispetto al Sole e alla Luna. Probabilmente in questo passo il participio epanakykloúmenon designa una contro-rivoluzione perché il verbo da cui si forma, sebbene significhi solamente ‘girare in tondo o muoversi in circolo’, in questo contesto assume il significato di ‘muoversi in circolo in direzione opposta’. In conclusione, dunque, i dialoghi platonici non forniscono nessuna prova inoppugnabile della conoscenza delle stazioni e delle retrogradazioni planetarie, e i rari passaggi in cui si è ritenuto di scorgerla possono essere spiegati in effetti in modo molto più semplice, ipotizzando una conoscenza dei diversi periodi siderali dei pianeti.
Aristotele e il contributo di Eudosso e Callippo
Il locus classicus citato da tutti i sostenitori della tesi che gli antichi fossero a conoscenza delle stazioni e delle retrogradazioni planetarie fin dal IV sec. a.C., è il cap. VIII del Libro XII della Metafisica di Aristotele, in cui l’autore si propone di determinare quanti «motori immobili» ci siano nel Cosmo e riassume quanto avevano detto gli astronomi precedenti:
Eudosso sostiene che il movimento di traslazione tanto del Sole quanto della Luna si compie nell’ambito di tre sfere, la più esterna delle quali, secondo lui, è quella delle stelle fisse, la seconda è quella che si muove nel cerchio che biseziona longitudinalmente lo Zodiaco, la terza è quella che si muove in un cerchio che è inclinato attraverso la latitudine dello Zodiaco (ma il cerchio secondo cui si sposta la Luna è inclinato secondo un angolo che è maggiore rispetto a quello secondo cui si sposta il Sole); il moto di traslazione di ciascun pianeta si attua mediante quattro sfere, e le prime due di queste sono identiche alle prime due del Sole e della Luna (infatti, la sfera delle stelle fisse è quella che imprime il movimento a tutte quante le altre sfere, e quella che è disposta in ordine dopo di essa e che compie la propria traslazione nel cerchio che biseziona lo Zodiaco, è comune a tutti i pianeti); invece la terza sfera di tutti i pianeti ha i suoi poli nel cerchio che biseziona lo Zodiaco e, infine, la quarta sfera compie la traslazione lungo un cerchio che è inclinato rispetto all’equatore della terza; a proposito, poi, della terza sfera, mentre ciascuno dei pianeti ha poli propri, Venere e Mercurio hanno entrambi i medesimi poli. Callippo era d’accordo con Eudosso circa la posizione delle sfere [ossia circa l’ordine delle loro distanze] ma, per quanto concerne il numero delle sfere, mentre assegnava a Giove e a Saturno lo stesso numero già assegnato da Eudosso, era invece del parere che, perché si potesse dare un conto preciso dei fenomeni, si dovessero aggiungere ancora due sfere sia al Sole sia alla Luna e una sola sfera a ciascuno degli altri pianeti. (Aristotele, Metaphysica, 1073 b 17-38)
Supponendo di non conoscere il commento di Simplicio a questo passo e volendo comprenderne il significato basandosi unicamente sulle testimonianze di altri autori del V e IV sec. a.C., per prima cosa si dovrebbe considerare il fatto che Aristotele riferisce le innovazioni o le osservazioni effettuate da Eudosso e Callippo, e non può certo essere considerato un cronista particolarmente fedele del pensiero dei suoi contemporanei e predecessori; in effetti, egli è solito riformulare le opinioni degli altri nel proprio linguaggio, in genere, anche se non esclusivamente, per criticarle. Ovviamente, non si vuole sostenere che Aristotele abbia frainteso il pensiero di Eudosso e di Callippo, bensì che non si dovrebbe dare per scontato che egli ne abbia riportato correttamente le parole e il loro senso: per esempio, anche se l’idea che i moti degli oggetti celesti sono determinati da una serie di sfere concentriche è uno dei motivi più ricorrenti nel De caelo in conseguenza dei ragionamenti sviluppati da Aristotele in questo trattato, ciò non significa che la stessa idea fosse condivisa anche da Eudosso e da Callippo. Questi ultimi, infatti, avrebbero potuto riferirsi ai diversi tipi di moto effettuati dai pianeti, moto che Aristotele potrebbe aver attribuito all’azione di un numero corrispondente di sfere, disposte secondo un certo ordine; se così fosse, ne conseguirebbe che, se il progetto di salvare o spiegare i fenomeni è presente in questo passo, dovrebbe essere considerato una conseguenza accidentale e, forse, inavvertita dell’originale obiettivo aristotelico di determinare il numero dei motori immobili presenti nel Cosmo.
Quali sono, dunque, secondo Aristotele, i fenomeni che Eudosso e Callippo si proponevano di spiegare con le loro teorie? Il primo punto da considerare è che in tutto il corpus aristotelico non vi è alcuna prova consistente della conoscenza delle stazioni e delle retrogradazioni dei cinque pianeti. Nelle sue opere Aristotele parla spesso dei pianeti, ma è raro che faccia menzione dei loro moti se non per osservare che si tratta di fenomeni complessi. Oltre al Libro XII della Metafisica, gli altri passi che descrivono in modo dettagliato i moti planetari appartengono ai Meteorologica, nella sezione dedicata alla discussione delle diverse teorie sulle comete (Tav. V). Se, dunque, nell’intero corpus aristotelico non c’è alcuna prova della conoscenza delle stazioni e delle retrogradazioni planetarie, non si può dare per certo che il passo della Metafisica citato si riferisca proprio a questi fenomeni; si dovrebbe anzi farne una lettura alternativa, che non presupponga questa conoscenza e che si accordi con ciò che sappiamo della scienza del cielo greca del V e del IV sec. a.C.: una lettura che sia coerente con le affermazioni di carattere astronomico presenti negli altri scritti di Aristotele e che non richieda, o presupponga, la conoscenza delle stazioni e delle retrogradazioni planetarie.
Durante il V e il IV sec. a.C., i Greci erano particolarmente interessati allo studio dei fenomeni celesti osservabili sulla linea dell’orizzonte. Infatti, come dimostrano il De aëre, aquis, locis di Ippocrate di Coo e altri trattati medici, gli antichi scrutavano l’orizzonte per osservare il sorgere e il tramontare del Sole, ma anche delle stelle e delle costellazioni. Gli scopi di queste osservazioni erano molteplici, e andavano dalla necessità di stabilire l’orientazione degli edifici a quella di creare un calendario solare, in cui il sorgere e il tramontare di determinate stelle e costellazioni fossero messi in relazione con i cambiamenti del tempo nelle diverse regioni - consentendo così una divisione dell’anno solare in periodi propizi alla semina o al raccolto delle messi - oltre che con le stagioni astronomiche (come scrive Esiodo ne Le opere e i giorni). Fu da questo insieme di esigenze che nacque il forte interesse manifestato dai Greci, in particolare nel IV sec. a.C., per la mappatura dei principali circoli di riferimento della sfera celeste, cosa che comportava l’individuazione delle stelle che sorgono e tramontano nello stesso punto del Sole durante i solstizi invernali ed estivi e durante i due equinozi.
È questa la premessa implicita del seguente brano di Eudosso contenuto nell’opera In Arati et Eudoxi Phaenomena commentariorum libri tres di Ipparco di Nicea (II sec. a.C.):
Su questo circolo [il tropico estivo] si trovano le parti centrali della [costellazione del] Cancro, quelle che attraversano per tutta la sua lunghezza il corpo del Leone, [le] parti superiori della Vergine, il collo del Serpente, tenuto stretto, la mano destra di Ingeniculus, la testa di Ofiuco, il collo e l’ala sinistra del Cigno, il piede del Cavallo e inoltre, la mano destra di Andromeda e la [regione] tra i suoi piedi, la spalla sinistra di Perseo e la sua gamba sinistra [più bassa], e ancora, le ginocchia dell’Auriga e le teste dei Gemelli; e poi si ricongiunge con le parti centrali del Cancro. (Ipparco di Nicea, In Arati et Eudoxi Phaenomena commentariorum libri tres, I, 2, 18)
Le numerose citazioni di Ipparco dei Phaenomena di Arato di Soli, confrontate con l’originale, si sono rivelate accurate; quindi si può presumere che anche le sue citazioni delle opere perdute di Eudosso siano ugualmente attendibili. Ciò non significa, tuttavia, che questo autore sia altrettanto attendibile come interprete del significato degli scritti di Arato e di Eudosso; al contrario, molte volte le analisi e le affermazioni di Ipparco sono chiaramente inconciliabili con i passi che egli cita per avvalorarle.
I fenomeni che gli uomini del V e IV sec. a.C. erano soliti osservare, guardando in alto, in pieno cielo, non erano molti: ovviamente, le fasi lunari, le eclissi di Sole e di Luna, vari occultamenti e fenomeni simili; in maniera analoga, inoltre, furono raggruppate le stelle nelle costellazioni. A quanto sembra, in questo periodo il principale metodo di indagine del cielo era rappresentato dall’osservazione della linea dell’orizzonte; quindi, supponendo che - secondo Simplicio - i quattro moti attribuiti da Eudosso a ciascuno dei cinque pianeti fossero stati individuati in base all’osservazione dell’orizzonte, cosa egli avrebbe potuto osservare in questo modo? In primo luogo, il fatto che ciascun pianeta sorge e tramonta ogni giorno; poi, che le sue prime apparizioni mattutine dopo il periodo di invisibilità sono separate da intervalli regolari; quindi, che queste apparizioni avvengono in un punto situato a nord o a sud di quello in cui il Sole sorge nello stesso giorno; infine, che la levata o il tramonto di ciascun pianeta coincidono a intervalli regolari con quelli di una determinata stella fissa. Quanto a Callippo, sarebbe sufficiente ipotizzare che egli avesse osservato una variazione dell’intervallo tra le prime visibilità mattutine, tale da giustificare l’aggiunta di un moto supplementare.
Se questa ipotesi fosse vera, ne conseguirebbe che fu Aristotele a dedurre da queste osservazioni l’esistenza di un certo numero di moti dipendenti da un sistema di sfere concentriche disposte in un determinato modo. La prima e la quarta osservazione non pongono alcun problema, essendo riconducibili rispettivamente alle prime due sfere, responsabili del moto giornaliero e di quello siderale. La seconda e la terza sono invece problematiche; si potrebbe però supporre che la terza sfera fosse responsabile del moto latitudinale e la quarta del legame (allora riconosciuto) tra lo spostamento latitudinale e un fenomeno sinodico come la prima visibilità mattutina (l’inclinazione dell’asse della quarta sfera rispetto alla terza determina la distanza massima del punto di levata o di tramonto del pianeta rispetto al punto di levata o di tramonto del Sole).
Questa ricostruzione non dà conto del fatto che il moto latitudinale di ogni pianeta si svolge in modo tale che i suoi punti di levata e di tramonto coincidono con quelli del Sole soltanto due volte nel corso del suo periodo siderale. L’errore di supporre che il moto latitudinale non sia legato al moto siderale è però una caratteristica reale del modello di Aristotele e si ritrova in tutte le descrizioni delle sue quattro sfere; inoltre, non è affatto chiaro se i realia astronomici possano costituire in questo caso un valido criterio di ricostruzione. Questa particolare ipotesi o lettura della testimonianza di Aristotele pone tuttavia un problema serio relativamente alla mancanza, nella letteratura greca dei secoli V e IV a.C., di testimonianze riguardanti l’esistenza di un programma di osservazione dei fenomeni planetari in rapporto alla linea dell’orizzonte. Al contrario, una tradizione di questo genere è ben documentata nella letteratura babilonese a partire dalla metà del VII sec. a.C.; così, invece di supporre che i Greci eseguissero direttamente questo tipo di osservazioni, si può forse immaginare che avessero appreso queste informazioni dai Babilonesi. Lo stesso Aristotele testimonia, a questo proposito, l’esistenza di scambi culturali con Babilonia, affermando che
accade invece il contrario: il Sole e la Luna compiono un minor numero di movimenti che non alcuni pianeti. Eppure questi sono più lontani dei primi dal centro e più prossimi al corpo primo; per alcuni astri, questo l’abbiamo potuto constatare anche con la nostra vista: abbiamo visto infatti la Luna passare in fase di metà davanti alla stella di Marte e Marte, nascosto dapprima dalla parte oscura di essa, uscire da quella visibile e luminosa. E cose analoghe ci riferiscono anche per gli altri astri gli Egizi e i Babilonesi, che fin dai tempi più antichi, e per moltissimi anni, hanno osservato questi fenomeni, e dai quali abbiamo molte notizie degne di fede (písteis) su ciascuno degli astri. (Aristotele, De caelo, 291 b 34-292 a 9)
L’ipotesi avanzata circa il significato del resoconto aristotelico delle teorie di Eudosso e Callippo è sufficiente a spiegare in modo adeguato la testimonianza di Aristotele e non contraddice quanto è detto su questo argomento nei documenti del V e del IV secolo. L’aspetto più interessante di questa ipotesi è che essa non esclude l’esistenza di un progetto per «salvare i fenomeni» e dell’ippopeda generata dai movimenti della terza e della quarta sfera, considerandoli però una conseguenza accidentale e non intenzionale del modello descritto da Aristotele.
Simplicio e le origini della scienza del cielo greca
Per quanto riguarda ciò che afferma Simplicio a proposito delle teorie di Eudosso e di Callippo, così come sono riportate da Aristotele nel Libro XII della Metafisica, è utile partire dal suo commentario al cap. XII del Libro II del De caelo di Aristotele che, per il suo grande interesse e per la sua notevole perspicuità converrà riportare con una certa ampiezza:
Per quanto riguarda i cinque pianeti, Aristotele, che riprende perfezionandola l’opinione di Eudosso, dice che essi si muovono per mezzo di quattro sfere, delle quali la prima e la seconda sono le stesse prime due sfere del Sole e della Luna e sono disposte come quelle. La prima, infatti, è la sfera che contiene tutte [le altre] per ciascun [pianeta] e ruota intorno all’asse del Cosmo da oriente a occidente nello stesso tempo della [sfera] delle [stelle] fisse; e la seconda, che ha i suoi poli sulla prima, effettua una rotazione in senso inverso, da occidente a oriente, intorno all’asse e ai poli del circolo che attraversa [le costellazioni dello] Zodiaco, nello stesso tempo impiegato da ciascun [pianeta] per attraversare il circolo zodiacale. Per cui, nel caso delle stelle di Mercurio e di Venere dice che la seconda sfera completa [la sua rotazione] in un anno; nel caso di Marte, in due anni; in quello di Giove, in dodici anni; e in quello di Saturno, che gli antichi chiamavano la stella di Helios, in trent’anni. Le due sfere restanti sono disposte presumibilmente in questo modo. I poli della terza [sfera] sono situati sul cerchio che attraversa [le costellazioni dello] Zodiaco, che s’immagina faccia parte della seconda sfera, e la sua rotazione avviene da sud a nord, nell’intervallo di tempo che ciascun [pianeta] impiega per passare da una fase a quella successiva, dopo aver attraversato tutte le configurazioni rispetto al Sole, un intervallo chiamato periodo sinodale da coloro che sono addentro alla scienza. Questo [periodo] è diverso per ciascun [pianeta]; di conseguenza, il tempo di rotazione della terza sfera non è lo stesso per tutti i pianeti, ma, secondo Eudosso, la stella di Afrodite [completa il suo periodo sinodico] in diciannove mesi; quella di Mercurio, in centodieci giorni; quella di Marte, in otto mesi e venti giorni; le stelle di Giove e di Saturno, ambedue in tredici mesi circa. La terza sfera si muove dunque in questa direzione e in intervalli di tempo di questa grandezza. Ma la quarta sfera, che trasporta anche essa i pianeti, ruota attorno ai poli di un circolo obliquo, poli peculiari a ciascun [pianeta]. Tuttavia, essa completa la sua rotazione nello stesso intervallo di tempo della terza, girando in direzione contraria a quella, da est a ovest. [Eudosso] afferma che questo circolo obliquo è inclinato rispetto al maggiore dei circoli paralleli della terza sfera [cioè, al suo equatore], un grande circolo che non è mai uguale né lo stesso per tutti. (Simplicio, In Aristotelis De caelo commentaria, ed. Heiberg 1894, 495.17-496.15)
Quanto all’aggiunta di una sfera supplementare da parte di Callippo per i moti di Mercurio, Venere e Marte, Simplicio dice semplicemente:
Callippo non ci ha lasciato alcun trattato in cui spieghi per quale ragione ha aggiunto queste sfere, né lo ha fatto Aristotele. Ma Eudemo ha indicato brevemente quali erano i fenomeni per salvare i quali egli pensava che queste sfere fossero state aggiunte, poiché dice che egli [Callippo] aveva detto che, se davvero gli intervalli di tempo che separano un solstizio dall’altro e un equinozio dall’altro differiscono tra loro quanto avevano detto Euctemone e Metone, allora per salvare i fenomeni non sono sufficienti tre sfere per ogni [pianeta], a causa della variazione che si manifesta chiaramente nei moti [del Sole e della Luna]. Ma per salvare quali [fenomeni] egli aggiunse una sfera a ciascuno dei tre pianeti, Marte, Venere e Mercurio, Eudemo lo ha indicato in modo chiaro e conciso. (ibidem, 497.15-24)
Alcuni studiosi ritengono che il testo presenti una lacuna dopo l’ultima frase, alla quale si pensava che dovesse seguire la spiegazione di Eudemo; la questione va riconsiderata alla luce della successiva osservazione di Simplicio, secondo cui
il sistema di sfere ruotanti in senso opposto non ha la capacità di salvare i fenomeni, come pensava anche Sosigene, che osserva: “malgrado ciò, [le sfere] dei seguaci di Eudosso in realtà non salvano i fenomeni, né quelli accertati più tardi, né quelli già conosciuti e accettati dagli stessi [seguaci di Eudosso]”. E cosa dire dei rimanenti [fenomeni], alcuni dei quali lo stesso Callippo di Cizico tentò di salvare, laddove Eudosso aveva fallito, se davvero [Callippo] riuscì a salvar[li]? (ibidem, 504.16-22)
Invece di supporre che la spiegazione di Eudemo a proposito della revisione di Callippo sia andata perduta, si potrebbe pensare che sia stata omessa la particella negativa ou nell’ultima frase, che andrebbe quindi letta in questo modo: «ma per salvare quali [fenomeni] Callippo aggiungesse una sfera a ciascuno dei tre pianeti, Marte, Venere e Mercurio, Eudemo non lo ha spiegato in modo breve e conciso». In altre parole, può darsi che Simplicio non riuscisse a trovare un senso nella presunta spiegazione di Eudemo.
La prima cosa da prendere in considerazione nell’esaminare la testimonianza di Simplicio è il fatto che si tratta di un resoconto. Ciò significa che non è possibile fare troppo affidamento sulla sua esattezza: anche se Simplicio si dimostra una fonte affidabile per quanto riguarda le citazioni di altri autori, è noto che non lo è affatto quando si tratta di riferire il significato delle loro parole, che spesso contamina con anacronismi e distorce attribuendovi finalità che non possiedono. Ciò non vuol dire che Simplicio abbia frainteso il pensiero di Eudosso e Callippo, ma soltanto che non è certo che avesse ragione e che la sua testimonianza dovrebbe essere considerata un’interpretazione. Quale peso bisogna attribuire allora alla testimonianza di Simplicio?
Le difficoltà più gravi nascono dal fatto che Simplicio inserisce le proprie osservazioni su Eudosso e Callippo in un contesto narrativo teso a ricondurre tutto il sapere filosofico greco alle opere di Platone e di Aristotele. In questa prospettiva, la storia dell’astronomia da Platone in poi è vista come una risposta alla questione, formulata inizialmente da Platone stesso, di spiegare i moti planetari mediante la combinazione di moti circolari, ordinati e uniformi. Posta in questi termini, però, la questione implica una brusca transizione: infatti, mentre la teoria documentata nei dialoghi platonici e nel Libro XII della Metafisica è omocentrica, all’epoca di Simplicio è ormai subentrata una visione decisamente non omocentrica dei moti planetari, rispondente ai modelli di calcolo elaborati da Tolomeo e basata sull’ipotesi di circoli eccentrici ed epiciclici (v. cap. XXXI). Quindi, il principale problema storiografico che Simplicio si trova ad affrontare è quello di specificare quando e perché questa transizione abbia avuto luogo.
Proclo di Costantinopoli, il maestro di Ammonio figlio di Ermia, a sua volta maestro di Simplicio, era stato forse il primo a pensare che l’astronomia si fosse sviluppata dall’esigenza di spiegare (e quindi ‘salvare’) quei fenomeni che apparivano inconciliabili con i principî fondamentali della teoria riguardante il funzionamento dei cieli. Inoltre, sempre Proclo, nello Schizzo delle teorie astronomiche afferma, portando a testimone l’autorità di Tolomeo, che Apollonio di Perge (262 ca.-180 ca.) aveva elaborato un metodo per determinare i punti stazionari dei moti planetari servendosi di un modello non omocentrico. Secondo Pappo (prima metà del IV sec. d.C.), Apollonio aveva seguito le lezioni degli allievi di Euclide, un’affermazione confermata anche dalla notizia, riferita da Proclo, secondo cui sia Archimede (287-212) sia Apollonio utilizzarono gli Elementi di Euclide come punto di partenza per le loro indagini. Inoltre, sempre Proclo colloca l’attività di Euclide tra la fine del IV e l’inizio del III sec. a.C.; non c’è dubbio, dunque, del fatto che queste date facessero parte di una cronologia ampiamente condivisa all’epoca di Simplicio.
Il progetto di schematizzazione della storia dell’astronomia greca, come una serie di stadi successivi della teoria planetaria a partire da Platone, rendeva dunque necessario giustificare la rapida dismissione della teoria omocentrica in un arco di tempo relativamente breve, cioè nei 60-80 anni che separano Aristotele e Callippo da Apollonio. Per questo problema della rapida transizione dalle teorie omocentriche a quelle non omocentriche Simplicio propone una soluzione ingegnosa e indubbiamente elegante, che nell’apparente verosimiglianza della sua struttura narrativa può apparire piuttosto convincente; è probabile, tuttavia, che non sia che una ricostruzione, basata sulle teorie astronomiche successive, delle fasi più antiche della scienza del cielo. Fra i numerosi indizi atti a dimostrare che la versione di Simplicio del processo storico, che portò i peripatetici ad abbandonare la teoria planetaria di Aristotele, è in realtà frutto della sua immaginazione, è sufficiente citarne uno soltanto.
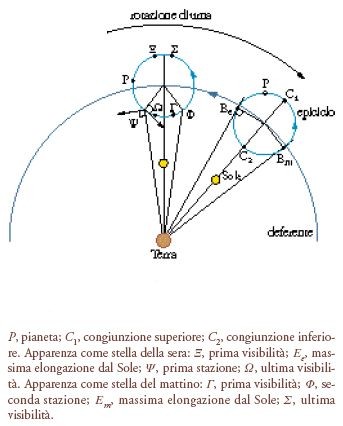
Il punto culminante del racconto di Simplicio circa il cambiamento della concezione peripatetica dell’omocentrismo è in parte definito dall’affermazione che i diametri apparenti di Venere e di Marte, osservati a occhio nudo, aumentano in misura considerevole quando si trovano a metà dei loro archi di retrogradazione. Ora, dato che tutte le fonti luminose di una certa intensità sembrano dotate di una superficie e che gli oggetti celesti più luminosi appaiono dotati di dimensioni maggiori del reale - un errore che fu corretto solamente dopo l’invenzione del telescopio - i documenti antichi tendono quasi sempre a identificare una variazione di luminosità con una variazione del diametro apparente. Nell’esaminare il racconto di Simplicio occorre tenere presenti queste considerazioni. Venere poi non è visibile a occhio nudo quando si trova al centro del suo arco di retrogradazione - una posizione nota anche come ‘congiunzione inferiore’ (fig. 4) -; anche concedendo a Simplicio un certo margine di imprecisione, e supponendo che intendesse parlare di Venere quando è prossima alla sua congiunzione inferiore, resta il fatto, empiricamente osservabile, che né il diametro apparente di questo pianeta, né la sua luminosità variano in modo significativo durante il suo ciclo sinodico, cioè nell’intervallo tra una prima visibilità mattutina e quella successiva. In effetti, le variazioni del diametro apparente di Venere sono molto al di sotto della soglia di risoluzione dell’occhio umano per quanto riguarda le differenze angolari; inoltre, dato che le fasi di Venere sono compensate dalle variazioni della distanza di questo pianeta dalla Terra, la sua luminosità varia in misura limitata e difficilmente percettibile a occhio nudo. Marte, al contrario, quando si trova al centro del suo arco di retrogradazione (e cioè in opposizione), è ben visibile, notevolmente più brillante del solito e, quindi, apparentemente più grande che in qualsiasi altro punto del suo ciclo sinodico. L’errore di Simplicio si spiega dunque con il tentativo di trattare Venere e Marte uniformemente. Secondo Tolomeo, i rapporti tra le distanze minime e massime di questi due pianeti dalla Terra erano grosso modo equivalenti, circa 7:1 in entrambi i casi. Così, partendo dal presupposto che alla variazione della distanza dalla Terra dovesse corrispondere una variazione della luminosità e della dimensione apparenti del pianeta, e dato che l’osservazione a occhio nudo rivela una notevole variazione della luminosità e della dimensione apparente nel caso di Marte, è probabile che Simplicio abbia ritenuto semplicemente che lo stesso dovesse verificarsi anche per Venere, commettendo così un duplice errore. In primo luogo, trasformò una conseguenza di una teoria, quella di Tolomeo, in un dato empirico, cosa piuttosto frequente presso gli antichi; in secondo luogo, ignorò il fatto che il comportamento di Venere è diverso da quello di Marte, non soltanto perché Venere quando si trova al centro del suo arco di retrogradazione è invisibile, ma anche perché la sua luminosità e la sua dimensione apparenti non subiscono alcuna variazione. È quindi estremamente improbabile che la dismissione della teoria omocentrica a favore di quella non omocentrica possa essere stata determinata in qualche modo dall’osservazione non strumentale delle variazioni della luminosità e della dimensione apparenti di Venere.
Il fatto che Simplicio sostenga invece questa tesi indica che la sua ricostruzione delle fasi più antiche della scienza del cielo greca è soltanto un racconto e non una storia nel senso moderno del termine.
Epicuro nella Lettera a Pitocle
Nel Libro X delle Vitae philosophorum Diogene Laerzio (forse verso la metà del III sec. d.C.) ci ha conservato tre lettere di Epicuro (341-270) a vari corrispondenti. Quella diretta a Pitocle, nella quale si affronta una «trattazione sintetica e concisa dei fenomeni celesti» (Ad Pythoclem epistula, 84), riveste un particolare interesse per gli storici dell’astronomia. Lo scopo principale della discussione è quello di raggiungere l’imperturbabilità e la serenità dell’animo, e secondo Epicuro questo obiettivo può essere raggiunto partendo dalla constatazione che ogni fenomeno ammette più di una spiegazione e rifiutandosi di compiere scelte arbitrarie tra le alternative disponibili. Verso la fine della lettera, egli fornisce due possibili spiegazioni del fatto che alcune stelle restino fisse e altre siano erranti:
può succedere che alcuni astri siano erranti, se accade che abbiano un moto di tal genere, e altri no, perché fin dal principio nel moto circolare da loro seguito alcuni furono compresi per necessità nel medesimo movimento vorticoso e regolare, altri in un movimento vorticoso con qualche irregolarità; ma è anche possibile che negli spazi attraverso i quali si muovono ci siano in certi punti correnti d’aria regolari che li spingono avanti sempre nella stessa direzione e li incendiano regolarmente, e invece in altri punti ci siano correnti irregolari, che determinano le differenze di moto da noi osservate. (Epicuro, Ad Pythoclem epistula, 112-113)
Dopo aver rimarcato i propri dubbi sulla possibilità che le stelle possano errare, Epicuro, per giustificare la distinzione tra stelle fisse ed erranti, avanza l’ipotesi che sin dall’inizio sia stato disposto che tutte le stelle dovessero muoversi in circolo e che la loro rivoluzione dovesse avvenire in alcuni casi in modo regolare e in altri in modo irregolare. In alternativa a quest’ipotesi, egli suppone che ogni stella sia prodotta dalla combustione dell’aria, e che le stelle fisse dispongano di un approvvigionamento uniforme di questo combustibile, al contrario di quelle erranti. Ora, la rivoluzione uniforme e regolare è senza dubbio quella effettuata ogni giorno dalle stelle fisse; ma cosa determina l’irregolarità e la mancanza di uniformità delle altre rivoluzioni? A questa domanda possono essere date molte risposte possibili: le rivoluzioni possono essere definite irregolari perché, per intervalli di tempo uguali, definiscono archi di diversa lunghezza, che possono avere tutti la stessa direzione oppure direzioni differenti; ma possono essere definite irregolari anche perché in esse si verificano occasionali deviazioni dal circolo, o perché combinano entrambi i tipi di irregolarità. Epicuro non è sufficientemente esplicito su questo punto, e non spiega a quale tipo di irregolarità intenda riferirsi, né in che modo avvenga la combustione dell’aria nel caso dei pianeti; di conseguenza, non è possibile dare per certo che, parlando di moti irregolari dei corpi celesti egli intendesse riferirsi proprio alle stazioni e alle retrogradazioni dei pianeti.
Nella stessa epistola, dopo aver inveito brevemente contro i partigiani dell’astronomia volgare, che ammettono un’unica causa per la diversità del comportamento delle stelle fisse e dei pianeti, Epicuro osserva:
che si vedano alcuni astri restare indietro rispetto ad altri può avvenire sia perché essi camminano più lentamente seguendo il medesimo giro orbitale, sia perché si muovono in senso opposto trascinati in tale direzione dallo stesso vortice, sia perché alcuni percorrono uno spazio maggiore e altri uno minore, pur muovendosi dello stesso moto rotatorio. L’affermare qualcosa di assoluto intorno a ciò è conveniente soltanto a coloro che vogliono sbalordire il volgo ignorante. (ibidem, 114)
In questo brano, esaminando la questione del ritardo apparente di alcuni pianeti rispetto agli altri, osservabile nel corso della loro rivoluzione, egli si riferisce al fatto che i pianeti hanno periodi (siderali) diversi, e avanza tre spiegazioni. La prima è che tutti i pianeti percorrono lo stesso circolo, ma a diverse velocità; la seconda è che i pianeti che sembrano più lenti, pur procedendo effettivamente in direzione opposta rispetto a quelli più veloci, essendo trascinati dalla rivoluzione di questi ultimi, finiscono per muoversi nella loro stessa direzione; la terza spiegazione è che i pianeti si muovono tutti nella stessa direzione e alla stessa velocità, ma alcuni sembrano più lenti perché seguono un’orbita più lunga.
Anche in questo caso, è possibile che la seconda spiegazione sia indice di una certa coscienza del fenomeno delle stazioni e delle retrogradazioni planetarie, ma non sarebbe corretto trasformare questa possibilità in certezza, essendo ugualmente possibile interpretare questa spiegazione come una generalizzazione di quella visione dei moti celesti già presente nel Timeo di Platone; e in entrambi i casi manca un esplicito richiamo al fatto che i pianeti più lenti retrocedono anche in rapporto alle stelle fisse. In conclusione, dunque, la lettera di Epicuro a Pitocle non contiene elementi sufficienti a dimostrare che i Greci possedessero già una chiara visione del fenomeno delle stazioni e delle retrogradazioni planetarie nel periodo compreso tra la fine del IV e l’inizio del III sec. a.C.
Apollonio di Perge: la testimonianza di Tolomeo nell’Almagesto
Nel cap. I del Libro XII dell’Almagesto, Tolomeo rivolge la sua attenzione agli archi di retrogradazione descritti sulla sfera celeste da ciascuno dei cinque pianeti quando essi viaggiano dalla prima stazione alla seconda (Tav. III). Poiché le amplitudini di questi archi variano periodicamente in ogni caso, egli si pone l’obiettivo di determinare l’arco massimo e quello minimo per ogni pianeta; cercando di dimostra - re che le sue computazioni delle amplitudini di questi archi concordano, per quanto è possibile, con i dati osservati. Tolomeo inizia con l’osservare che, per questa sorta di determinazione, «gli altri matematici e Apollonio di Perge dimostrano anticipatamente per il caso di una singola anomalia in relazione al Sole» le condizioni che determinano le posizioni dei punti stazionari in un modello epiciclico e in uno eccentrico. Il resto del capitolo è dedicato all’esposizione di una derivazione matematica dei punti stazionari in questi modelli; si tratta, quindi, di stabilire se gli argomenti trattati autorizzano a supporre che Apollonio di Perge fosse a conoscenza del fenomeno delle stazioni e delle retrogradazioni planetarie.
Generalmente si è ritenuto che la dimostrazione di Tolomeo di ciò che «gli altri matematici e Apollonio di Perge» avevano provato, fosse opera dello stesso Apollonio; ma, come ha osservato Toomer, Tolomeo in effetti oppone la dimostrazione contenuta nel cap. I del Libro XII dell’Almagesto a quelle elaborate dai teorici precedenti. Quali sono, dunque, i rapporti tra il contributo di Tolomeo alla risoluzione di questo problema e quelli dei suoi predecessori? Secondo Tolomeo, questi primi studiosi consideravano separatamente i due diversi modelli, eccentrico ed epiciclico; l’idea di combinarli è quindi probabilmente dello stesso Tolomeo, e non è dato sapere se Tolomeo fa uso del lavoro di altri matematici nella sua dimostrazione. Come ha notato Neugebauer, vi sono importanti analogie tra la dimostrazione di Tolomeo e alcuni teoremi dei Conica di Apollonio. Tuttavia, queste analogie potrebbero significare solamente che Tolomeo attinse dall’opera di Apollonio alcuni strumenti indispensabili per determinare la posizione dei punti stazionari nei modelli epiciclici ed eccentrici del moto planetario; in effetti, nel corso della sua dimostrazione Tolomeo impiega un teorema sui triangoli scaleni che attribuisce esplicitamente ad Apollonio. Ma con ciò si è ben lontani dal dimostrare che Apollonio avesse elaborato i suoi teoremi a questo scopo o tanto meno che avesse tentato di calcolare le posizioni dei punti stazionari, anche soltanto nell’ambito di uno studio generale delle proprietà matematiche dei modelli epiciclici ed eccentrici, e che fosse quindi a conoscenza del fenomeno delle retrogradazioni planetarie.
Con le parole «hoì te álloi mathēmatikoì kaì Apollṓnios ho Pergaíos» («gli altri ‘matematici’ e Apollonio di Perge»), Tolomeo potrebbe aver voluto dire semplicemente che Apollonio era l’autore di alcuni teoremi sui triangoli piani in - dispensabili alla dimostrazione delle posizioni dei punti stazionari, così come questa era stata successivamente formulata da altri matematici, che non sono nominati. Naturalmente, le parole di Tolomeo implicano anche il concetto che Apollonio fosse lui stesso un ‘matematico’, nel senso in cui questo termine è utilizzato nell’Almagesto, cioè uno studioso della scienza del cielo che si proponeva di spiegare, inter alia, il complesso dei moti celesti come il prodotto della combinazione di una serie di moti circolari e uniformi. Sfortunatamente, però, Tolomeo non ci dice se Apollonio deve essere considerato un matematico per la sua partecipazione diretta al progetto perseguito dagli altri matematici o solamente per aver contribuito a produrre risultati fondamentali per la realizzazione di questo.
Allo stesso tempo, sembra ragionevole domandarsi se Apollonio, matematico di innegabile talento, si sia posto effettivamente il problema delle stazioni planetarie. Tale problema rappresentava uno dei principali ostacoli che qualunque teorico orientato a una rappresentazione geometrica e cinematica dei moti planetari come prodotto di movimenti circolari e uniformi si trovava a dover affrontare. Non si può escludere, inoltre, che Apollonio fosse venuto a conoscenza delle caratteristiche dei moti planetari da altre fonti, più o meno direttamente riconducibili ai Babilonesi: nel secolo successivo alla conquista di Babilonia da parte di Alessandro nel 330 a.C. si verificò certamente una notevole diffusione della scienza del cielo babilonese, come attesta il papiro Hibeh 27 (v. sopra). Comunque, alla luce delle testimonianze disponibili, l’opera di Apollonio sembra essere rimasta ai margini dell’interesse del mondo greco-latino per la scienza del cielo nei due o tre secoli successivi, dato che nella letteratura astronomica greco-latina antecedente a Tolomeo non vi è alcun accenno all’esistenza di ulteriori commentari sul problema dei punti stazionari, anche in quei casi in cui sarebbe lecito attenderselo. Quindi, per ciò che riguarda Apollonio, quello che si può desumere dalla lettura del brano citato dell’Almagesto è soltanto che egli sia stato l’autore di alcune fondamentali scoperte nel campo della geometria piana, perché ciò è tutto quello che questo brano richiede.
‘Salvare i fenomeni’: le origini del progetto di spiegazione dei moti planetari
Fino alla fine del I sec. a.C. nella letteratura sulla scienza del cielo greco-latina manca semplicemente qualunque accenno ai fenomeni planetari a cui allude Simplicio nella sua lettura del Libro XII della Metafisica di Aristotele, cioè alle stazioni e alle retrogradazioni, e perfino una terminologia per designarli. Nessuno dei passi nei quali sono stati individuati riferimenti al fenomeno delle stazioni e delle retrogradazioni planetarie richiede in realtà una lettura di questo tipo e, di conseguenza, l’ipotesi secondo cui il progetto di «salvare i fenomeni» delle stazioni e delle retrogradazioni planetarie sarebbe stato formulato nel periodo compreso tra il V e il II sec. a.C. si dimostra priva delle basi necessarie. Esaminando l’intero corpus dei documenti greci e latini che ci sono pervenuti, non si trovano casi diretti (databili) di parole o espressioni che indichino questi particolari fenomeni fino alle opere di Marco Tullio Cicerone (106-43 a.C.), Diodoro Siculo e Vitruvio. Dagli scritti di Diodoro e Vitruvio risulta evidente che il contesto all’interno del quale le idee riguardanti questo tipo di fenomeni planetari divennero note agli Elleni e ai Romani non fu, come suggerisce Simplicio, quello della filosofia e della cosmologia platoniche e aristoteliche, né quello della scienza del cielo ellenica e romana, sviluppatesi in maniera parzialmente autonoma fino al tardo II sec. a.C. I Greci e i Romani vennero a conoscenza dei principali moti apparenti dei pianeti non attraverso un programma più o meno formale di osservazioni, ispirato da interessi di carattere filosofico o comunque derivato da questi interessi, bensì in seguito alla diffusione delle tavole planetarie utilizzate dagli astrologi per formulare gli oroscopi. Ma l’astrologia oroscopica, una disciplina volta a predire il destino degli individui sulla base delle posizioni occupate dai sette pianeti al momento della nascita, fu introdotta nel mondo greco e romano sul finire del II sec. a.C., se non ancora più tardi, a partire dall’Egitto. Occorre quindi determinare quando e in quali circostanze i Greci e i Romani giunsero a porsi - per la prima volta - il problema di trovare una spiegazione del fenomeno delle stazioni e delle retrogradazioni planetarie, e in che modo cercarono di risolverlo.
Plutarco su Aristarco e il moto della Terra
I Greci utilizzavano diverse espressioni per designare l’idea di «salvare i fenomeni» o le «apparenze», espressioni che ricorrono in contesti diversi e indicano progetti differenti. In alcuni casi ci si propone di rendere conto di un’apparente irregolarità e quindi di salvarla, spiegandola. In altri casi, il progetto è quello di spiegare una regolarità e quindi di preservarla o mantenerla; in altri ancora il significato dell’espressione è piuttosto vago. Alla luce di queste precisazioni, a proposito dell’espressione che è usata da Simplicio (dia)sṓzein tà phainómena, è utile operare una distinzione tra l’espressione, «salvare i fenomeni», e il progetto stesso. A quanto risulta, la formula in questione appare per la prima volta, precedendo tutte le formulazioni affini, in un dialogo immaginario contenuto nel De facie in orbe lunae di Plutarco di Cheronea (n. 50 ca. - m. dopo 120). È abbastanza sorprendente che, in un contesto astronomico, Plutarco impieghi questa espressione in riferimento non ai moti dei cinque pianeti, bensì alla tesi secondo cui la Terra si muove attorno al Sole e ruota intorno al proprio asse. Scrive Plutarco che Lucio scoppiò a ridere e poi disse: «Purché, mio caro, tu non ci intenti un processo per empietà come quello che Cleante pretendeva dai Greci contro Aristarco di Samo, che egli accusò di perturbare il focolare dell’Universo nel tentativo di salvare i fenomeni con l’ipotesi che il cielo resti immobile mentre la Terra percorre un’orbita obliqua rotando al contempo intorno al proprio asse» (Plutarco, De facie in orbe lunae, 923a).
Dall’osservazione di Lucio si deduce che la levata e il tramonto dei corpi celesti osservati ogni giorno sulla linea dell’orizzonte, rispettivamente a oriente e a occidente, e lo spostamento da nord a sud del punto situato a oriente in cui sorge il Sole, osservato nel corso dell’anno lungo la linea dell’orizzonte, potevano essere ‘salvati’ (cioè spiegati) attraverso due ipotesi. Secondo la prima il Sole e i cieli si muovono intorno alla Terra, che rimane immobile al centro. Per la seconda, invece, la Terra ruota intorno al proprio asse e si muove lungo un’orbita circolare intorno al Sole, mentre i cieli rimangono immobili: la scelta tra le due ipotesi è presentata come una questione di carattere religioso. Ma è davvero possibile attribuire ad Aristarco la formulazione del progetto di «salvare i fenomeni» e collocare quindi nel III sec. a.C. l’origine di questo programma di spiegazione che pochi secoli dopo fu utilizzato per valutare le nuove informazioni sui pianeti e sui loro moti? Non ci è pervenuto nessun trattato di Aristarco che confermi l’indicazione di Plutarco, e la questione relativa all’esistenza di un tale trattato è legata a un sottile problema di interpretazione del primo testo in cui si attribuisce ad Aristarco la tesi del moto della Terra, ossia la prefazione all’Arenarius del suo contemporaneo Archimede (v. cap. XVIII).
Secondo Archimede, Aristarco sosteneva le tesi seguenti (Tav. VI): le stelle fisse e il Sole rimangono immobili; la Terra si muove lungo una circonferenza al cui centro si trova il Sole; la sfera delle stelle fisse è così grande che il rapporto tra la circonferenza lungo la quale si muove la Terra e il raggio della sfera celeste è uguale a quello esistente tra il centro di una sfera e la sua superficie (le prime due tesi corrispondono interamente a ciò che afferma Plutarco nel brano citato del De facie in orbe lunae). Tuttavia, Archimede tace sui motivi che indussero Aristarco a postulare il moto terrestre, e la sua attenzione sembra interamente rivolta alla tesi secondo cui tra un punto e la superficie di una sfera può esservi una proporzione. Poiché ritiene che questa tesi sia errata - questi relata, per esempio, se moltiplicati, non possono superarsi reciprocamente (cfr. Euclide, Elementa, lib. V, def. 3 e 4) - egli reinterpreta l’analogia di Aristarco. Dal suo punto di vista, Aristarco intendeva in realtà affermare che il rapporto tra la Terra e la sfera che contiene la circonferenza del moto terrestre è uguale al rapporto tra questa sfera e la sfera celeste.
Benché la sua revisione sia motivata da preoccupazioni di carattere tecnico relative alla nozione di rapporto, e forse dalla natura del progetto intrapreso nell’Arenarius, Archimede la giustifica aggiungendo che Aristarco «adatta le dimostrazioni dei fenomeni a una supposizione di tal genere». Non è precisato affatto, però, quali fossero questi fenomeni e in che preciso modo Aristarco li avesse dimostrati. Così, in mancanza di ulteriori informazioni da parte di Archimede, non siamo in grado di stabilire con certezza se la dimostrazione a cui si fa riferimento fosse una deduzione matematica, o un’argomentazione a sostegno di una tesi, o persino un’illustrazione del modo di operare di uno schema o di una configurazione, per non menzionare che tre possibilità. Inoltre, in mancanza di argomenti, non possiamo sostenere che in questo caso si intenda per ipotesi un tema da sottoporre alla discussione piuttosto che il risultato di una discussione comune o il presupposto o la premessa di un ragionamento deduttivo. In breve, non possiamo stabilire in modo aprioristico a quali dei vari possibili significati dei termini ‘dimostrazione’ (apódeixis) e ‘ipotesi’ (hypóthesis) Archimede intenda riferirsi.
La testimonianza di Archimede spinge a domandarsi che cosa pensasse riguardo ai cinque pianeti la maggior parte degli astronomi a cui si fa riferimento, e se si prendesse la pena di considerarli come oggetti di studio distinti. Vi è infine un altro problema: nel De magnitudinibus et distantiis Solis et Lunae, un trattato abitualmente attribuito ad Aristarco, si suppone infatti che il Sole e la Luna si muovano lungo circonferenze omocentriche intorno alla Terra. Secoli dopo, Seneca (4 a.C. ca.-65 d.C.) nelle Naturales quaestiones scriveva che
l’analisi particolareggiata di questi problemi servirà anche al preciso scopo di farci sapere se l’Universo ruota mentre la Terra sta ferma oppure la Terra gira mentre l’Universo sta fermo. Vi furono infatti quelli i quali sostennero che siamo noi a essere trasportati a nostra insaputa dalla Natura e che le albe e i tramonti non dipendono dal movimento del cielo, ma che siamo noi stessi a sorgere e a tramontare: è un argomento degno di attento studio al fine di sapere in quale collocazione fisica ci troviamo, se ci è toccata in sorte la dimora più pigra o la più veloce, se Dio spinge intorno a noi tutte le cose o invece spinge noi. (Seneca, Naturales quaestiones, VII, 2.3)
Da questo brano si può dedurre che la tesi secondo cui la Terra ruota intorno al proprio asse probabilmente serviva a spiegare i fenomeni osservati ogni giorno lungo la linea dell’orizzonte e, in particolare, le levate e i tramonti delle stelle fisse; tuttavia, Seneca non menziona specificamente il moto della Terra intorno al Sole, un moto che avrebbe certamente semplificato la spiegazione delle levate e dei tramonti dei corpi celesti nell’intero corso dell’anno. Sembra lecito dubitare che egli volesse effettivamente riferirsi ad Aristarco, in quanto poteva invece riferirsi semplicemente alla disputa tra Aristotele e coloro che - pur seguendolo nel ritenere che la Terra si trovasse al centro del Cosmo - rifiutavano l’argomento contenuto nel De caelo secondo cui i moti delle costellazioni nel cielo notturno confermerebbero l’idea della Terra immobile al centro di una sfera celeste che si muove in circolo. A sua volta, Aristotele, sempre nel De caelo, cita la tesi presente nel Timeo di Platone secondo cui la Terra si trova al centro del Cosmo e possiede un moto rotatorio assiale: questa tesi è attestata, di conseguenza, in un documento che risale a un periodo antecedente a quello in cui visse Seneca, in un contesto differente da quello indicato dalla testimonianza di Archimede su Aristarco. Infine, l’ipotesi di Aristarco sul moto della Terra intorno al Sole è menzionata da Stobeo, un autore del V sec. d.C., nelle sue Eclogae physicae et ethicae: «Aristarco sostiene che il Sole è uno dei (corpi celesti) fissi, e che la Terra si muove attorno all’orbita del Sole ed è investita dall’ombra a seconda della sua inclinazione» (Stobeo, Eclogae physicae et ethicae, I, 25, 3 k). Anche in questo caso non sono precisati i motivi su cui si fondavano le affermazioni di Aristarco, anche se si è supposto, basandosi sul riferimento all’inclinazione della Terra, che questi intendesse spiegare le differenze climatiche tra le stagioni.
Il De facie in orbe lunae di Plutarco è dunque il primo testo, tra quelli che ci sono pervenuti, in cui si afferma esplicitamente che Aristarco cercò di «salvare i fenomeni». Come Archimede prima di lui, Plutarco non precisa quali fossero questi fenomeni, o che altro significasse ‘salvarli’ se non spiegarli come eventi regolari. La questione non è risolta definitivamente né chiarita neanche dalle sue osservazioni successive, contenute nelle Platonicae questiones, secondo cui Aristarco e Seleuco (II sec. a.C.) avevano descritto i due moti terrestri anche se il primo sotto forma di ipotesi e il secondo come realtà oggettiva. Thomas L. Heath suppone che tale differenza fosse basata sulla distinzione esistente, in materia di scienza del cielo, tra discorso matematico e discorso fisico: secondo Heath, i matematici si proponevano solamente di enunciare ipotesi che consentissero di spiegare i fenomeni, mentre i fisici dovevano stabilirne la realtà oggettiva. Come vedremo oltre, probabilmente questa supposizione non è opportuna e si rivela invece anacronistica. Inoltre, la differenza in questione può essere certamente spiegata in altri modi: per esempio, Plutarco forse sapeva che la cosmologia del De magnitudinibus, che ai suoi tempi era attribuito ad Aristarco, non è eliocentrica e quindi tendeva a supporre che Aristarco avesse sostenuto la tesi dei vari moti della Terra non come una realtà oggettiva, ma come un soggetto o argomento di discussione.
Sembra quindi che Plutarco, utilizzando l’espressione «salvare i fenomeni» in riferimento ad Aristarco, abbia proiettato nel passato un progetto formulato successivamente, in un diverso campo o contesto, interpretando le osservazioni di Archimede a proposito di Aristarco alla luce di un programma originato dagli sviluppi successivi della scienza del cielo ellenico-romana. Questi sviluppi concernevano i primi tentativi degli autori ellenici e latini del periodo fra il I sec. a.C. e il I sec. d.C. di spiegare i moti dei cinque pianeti in un modo più accurato rispetto ai loro predecessori. La principale testimonianza in tal senso è la Introductio astronomiae di Gemino (attivo verso il 70 a.C.), un’opera redatta all’inizio del I sec. d.C., soltanto pochi decenni prima del De facie di Plutarco. Scrive Gemino:
È stabilito, per quanto riguarda l’astronomia nel suo insieme, che il Sole, la Luna, e i cinque pianeti si muovano in circolo a velocità costante, e in direzione opposta alla [rotazione giornaliera] del Cosmo. I pitagorici, infatti, che per primi giunsero a questo genere di indagini, supponevano che i moti del Sole, della Luna, e dei cinque pianeti fossero circolari e regolari. Trattandosi di oggetti divini ed eterni, essi non ammettevano alcun disordine, per esempio che a volte [questi oggetti] si muovessero più rapidamente, a volte più lentamente e a volte non si muovessero affatto, evento che, nel caso dei cinque pianeti, essi chiamavano ‘stazione’. Neppure riguardo a un uomo beneducato e ordinato si ammetterebbe che possa viaggiare attraverso percorsi irregolari. In effetti, le necessità della vita sono spesso causa di lentezza e di velocità per gli uomini, ma, per la natura imperitura dei corpi celesti, non può essere introdotta alcuna causa di velocità o di lentezza. Per la quale ragione essi avevano formulato questo [quesito]: come si possono spiegare i fenomeni attraverso moti circolari e regolari? In seguito, forniremo una spiegazione per gli altri corpi celesti in un altro luogo; ora, invece, riguardo al Sole, dimostreremo perché, benché si muova a una velocità costante, esso attraversi archi uguali in tempi ineguali. (Gemino, Introductio astronomiae, I, 19-22)
Gemino fa riferimento alle idee dei pitagorici, riferendosi probabilmente ai suoi immediati predecessori e contemporanei. Tra il I sec. a.C. e il I sec. d.C. si ebbe infatti una rinascita del pitagorismo fra eminenti personalità greche e romane quali Eudosso di Alessandria (attivo nel 25 a.C. ca.), Publio Nigidio Figulo (m. nel 44 a.C.) e il santo itinerante Apollonio di Tiana (I sec. d.C.). In questa fase di rinascita, il pitagorismo non era una dottrina monolitica: per quanto riguarda specificamente la teoria planetaria, è importante ricordare che Nigidio Figulo - che nel 57 a.C. rivestì la carica di pretore ed era amico di Cicerone - era un appassionato studioso del pitagorismo e dell’astrologia, e che i suoi scritti sono probabilmente la fonte all’origine delle incursioni nel campo della scienza del cielo (teoria planetaria inclusa) intraprese da Vitruvio nel Libro IX del De architectura.
Il progetto di spiegare le retrogradazioni e le stazioni dei cinque pianeti iniziò quindi a delinearsi durante il I sec. a.C., parallelamente ai primi tentativi degli autori greco-latini di risolvere il problema del moto planetario in modo più accurato rispetto al periodo precedente, e fu designato per la prima volta come obiettivo specifico degli astronomi in un trattato scritto nella prima metà del I sec. d.C. L’espressione «salvare i fenomeni», tuttavia, appare per la prima volta in un testo redatto alcuni anni dopo questi fatti, e non vi è alcun modo di stabilire se fu coniata per sintetizzare questo nuovo progetto della scienza del cielo o se invece fu presa in prestito da un progetto analogo, formulato in un campo diverso. Ciononostante, è presumibile che lo scopo della scienza del cielo greco-latina fosse precisamente quello di spiegare le stazioni e le retrogradazioni planetarie, mentre non molto tempo dopo il suo ambito di applicazione si estese alla definizione delle specifiche relazioni teoriche esistenti tra un qualsiasi presunto moto celeste e i relativi fenomeni.
Diodoro, Cicerone e Vitruvio
Le principali fonti del I sec. a.C. per quanto riguarda le origini del progetto destinato a «salvare i fenomeni» planetari delle stazioni e delle retrogradazioni, prima dell’opera di Gemino, sono Diodoro, Cicerone e Vitruvio. Questi autori testimoniano una sorprendente evoluzione concettuale nel processo di definizione dei moti planetari, e le loro opere costituiscono le più importanti fonti letterarie sulla ricezione della scienza del cielo babilonese ed egizia nel contesto intellettuale ellenico-romano antecedente al I sec. d.C.
Diodoro giunge alla trattazione di questo tema in modo piuttosto naturale, perché esso fa parte del più vasto progetto di narrare la storia di tutti i popoli dai tempi mitologici fino alla sua epoca; progetto che includeva la descrizione dettagliata delle conoscenze sul cielo a cui erano pervenuti questi popoli, e in particolare gli Egizi, i Caldei di Babilonia e gli Elleni. Le descrizioni di Diodoro sono preziose poiché rivelano quali criteri culturali informassero la comprensione dell’astronomia nel I sec. a.C. Egli afferma che i sacerdoti egizi avevano accuratamente osservato le stelle:
le posizioni e i moti dei corpi celesti sono stati osservati con grande attenzione dagli Egizi, più che da ogni altro popolo. Infatti, essi possiedono delle annotazioni riguardanti ciascuno di essi, frutto di osservazioni incredibilmente antiche, e hanno studiato in particolare i moti dei pianeti, i loro periodi, le loro stazioni e, inoltre, gli influssi esercitati da ciascuno di essi in relazione alla nascita delle creature viventi - quali benefici o malefici possono produrre - poiché presso di loro l’entusiasmo per questi argomenti era molto ammirato sin dai tempi antichi. (Diodoro Siculo, Bibliotheca historica, I, 81, 4-5)
Diodoro descrive la scienza del cielo praticata dagli Egizi come una combinazione di astrologia oroscopica, giudiziaria e meteorologica, volta a formulare predizioni basate sulla disposizione dei corpi celesti in un momento dato, riguardanti gli eventi della vita degli individui, dello Stato e il tempo atmosferico. Oggi sappiamo che l’astrologia oroscopica fu un’innovazione di origine mesopotamica e non egizia; sembra tuttavia che essa sia giunta per la prima volta nel mondo ellenico e in quello romano durante il I sec. a.C. attraverso l’Egitto. Diodoro sostiene che i progressi più significativi nel campo dell’astronomia greca - compiuti da figure tradizionalmente illustri come Democrito di Abdera, Enopide di Chio ed Eudosso di Cnido - derivavano dai loro viaggi in Egitto e dagli insegnamenti loro impartiti dai sacerdoti egizi. Dal suo punto di vista, dunque, l’astronomia egizia era la fonte dei principî fondamentali della scienza del cielo ellenica (per es., di quello secondo cui il moto annuale del Sole si svolge verso est, lungo un percorso circolare obliquo all’equatore celeste), come pure dei suoi risultati generali. Diodoro giunge al punto di attribuire agli Egizi tutto ciò che nel suo tempo si conosceva delle scoperte di Eudosso in campo astronomico; inoltre, in una fase successiva dello svolgimento del trattato, egli attribuisce l’astrologia oroscopica a quelli che definisce i Caldei di Babilonia, e registra persino la rivendicazione egizia secondo cui questi avevano appreso da loro ciò che sapevano sulla scienza del cielo. Tuttavia, sebbene ammiri l’abilità dei Caldei e degli Egizi nel pronosticare il destino degli individui interpretando le posizioni dei corpi celesti alla loro nascita, non allude mai al fatto che questo fosse un compito appropriato, o persino desiderabile, nel contesto della scienza del cielo ellenica e romana, e non riconosce mai agli astronomi ellenici e romani un qualche interesse o una qualche competenza in materia di astrologia oroscopica. Diodoro narra ai suoi lettori che i cinque pianeti effettuano apparentemente stazioni e retrogradazioni, ma non sembra essere consapevole del fatto che questa constatazione potesse essere in contraddizione con qualsiasi credenza del suo ambito culturale sugli dei e sui cieli.
Nella sua opera De natura deorum, Cicerone non si limita a una semplice descrizione dei moti planetari, ma sottolinea il fatto che, nonostante le apparenze, questi sono del tutto costanti e regolari:
Ma particolarmente straordinari sono i moti di quelle cinque stelle che sono erroneamente chiamate erranti: in realtà non è errante ciò che mantiene costanti e regolari i movimenti diretti, retrogradi, e tutti gli altri per tutta l’eternità. E questo fenomeno è ancora più straordinario nel caso delle stelle di cui parliamo, perché esse sono ora in occultazione, ora ricompaiono, ora si avvicinano, ora si allontanano, ora precedono, ora seguono, ora si muovono più rapidamente, ora più lentamente, ora non si muovono affatto ma si fermano per un certo periodo. (Cicerone, De natura deorum, II, 51)
In questo brano si trova la prima menzione del fatto che le stazioni e le retrogradazioni dei cinque pianeti potevano dare origine a un problema, e per risolverlo Cicerone aggiorna efficacemente l’osservazione del Forestiero ateniese nelle Leggi di Platone, secondo cui ogni pianeta in realtà non è erratico, ma si muove costantemente lungo una singola orbita circolare, e la consuetudine di chiamarli «stelle erranti» è blasfema (v. sopra). Nel dialogo di Cicerone, redatto molto più tardi rispetto alle Leggi, in un’epoca in cui la natura di questi oggetti celesti erranti era capita decisamente meglio, l’affermazione secondo cui i pianeti errano non è considerata né meritevole di disapprovazione né empia, e si giudica inadeguato il predicato ‘errante’ riferito ai pianeti per il semplice motivo che le irregolarità osservate nel loro moto in realtà si ripetono regolarmente e si mantengono inalterate per l’eternità; il Cecilio Balbo di Cicerone finisce per allontanarsi dalla teoria planetaria del Forestiero ateniese e trasforma il fatto che i pianeti sembrano errare nei modi descritti osservando semplicemente che, poiché il loro errare è periodico – come dire regolare –, essi quindi non sono realmente erranti.
Questo nuovo punto di vista si collega alle tesi espresse nel Libro IX del trattato De architectura, redatto da Vitruvio probabilmente non molto dopo la battaglia di Azio (che ebbe luogo nel 30 a.C.). Vitruvio, architetto e ingegnere militare al seguito di Gaio Giulio Cesare (102/100-44 a.C.), dedicò la sua opera ad Augusto, pronipote e figlio adottivo di Cesare. L’argomento trattato nel Libro IX, la gnomonica, consente all’autore di introdurre un breve excursus sulla sfera celeste, sulla fascia zodiacale e sui moti dei sette pianeti: «Mentre queste costellazioni in numero di 12 occupano ciascuna la dodicesima parte del cielo e compiono la loro rivoluzione incessantemente da est a ovest, la Luna, Mercurio, Venere, il Sole stesso e anche Marte, Giove e Saturno passano attraverso queste costellazioni con moto di senso contrario, nel loro giro del cielo da ovest a est, come percorrendo una salita gradino per gradino, ciascuno con un’orbita di grandezza diversa» (Vitruvio, De architectura, IX, 1, 5).
In questo brano, il moto (diretto) verso est di tutti i sette pianeti è circolare, ha al suo centro la Terra e si svolge in direzione opposta alla rotazione giornaliera della sfera celeste. Le orbite descritte dai pianeti hanno una diversa grandezza e sono paragonate da Vitruvio ai gradini di una scala che si eleva fino alla sfera celeste. Quindi, dopo aver stabilito i valori dei periodi siderali della Luna e del Sole (gli intervalli di tempo in cui la Luna e il Sole percorrono i loro rispettivi circuiti e ritornano a un dato segno zodiacale, che corrisponde alla dodicesima parte del circolo zodiacale), Vitruvio afferma che: «Quanto a Mercurio e a Venere, quando, avendo come centro i raggi del Sole cui fanno da corona con i loro movimenti, subiscono retrogradazioni e rallentamenti, essi nel corso del loro movimento circolare fanno anche delle fermate e si trattengono nello spazio di alcune costellazioni» (ibidem, IX, 1, 6).
Così, l’autore segnala il fatto che i moti di Mercurio e di Venere seguono percorsi che mantengono questi due pianeti vicino al Sole.
Secondo una lunga tradizione interpretativa, in questo brano Vitruvio introduce l’eliocentrismo, richiamandosi a una cosmologia in cui il Sole è al centro dell’Universo, senza riguardo per la coerenza del suo excursus. Ma, come ha osservato J.L.E. Dreyer, le parole di Vitruvio possono significare, altrettanto verosimilmente, che questi pianeti si muovono lungo epicicli i cui centri giacciono su delle circonferenze concentriche all’orbita del Sole, dette ‘deferenti’. La frase «avendo come centro» è troppo vaga per stabilire se l’autore volesse affermare che il Sole è il centro dei loro epicicli o piuttosto che questi pianeti sembrano girare come avendo il Sole al centro, perché i centri dei loro epicicli giacciono sempre sulla linea retta che congiunge la Terra al Sole. Seguendo Dreyer, supponiamo che Vitruvio intendesse affermare che Mercurio e Venere si muovono su epicicli e che la configurazione fosse quella illustrata nella precedente fig. 4: un pianeta P, Mercurio o Venere, è raffigurato mentre si muove con moto uniforme sulla circonferenza di un cerchio, detto ‘epiciclo’, il cui centro descrive, ancora con moto uniforme, la circonferenza di un altro cerchio, detto ‘deferente’, intorno alla Terra (ai fini della nostra analisi è sostanzialmente irrilevante che il Sole sia collocato al centro dell’epiciclo oppure sulla linea che congiunge il centro del deferente al centro dell’epiciclo). La linea che congiunge la Terra al centro dell’epiciclo è orientata in direzione del Sole, il quale, se ci basiamo sulla supposizione, attendibile ma non certa, secondo cui l’ordine in cui sono disposti i pianeti nel De architectura (IX, 1, 6-10) corrisponde al loro ordine naturale, è qui raffigurato mentre si muove lungo un percorso circolare al di sotto di Mercurio e di Venere. Il moto sull’epiciclo e quello sul deferente si svolgono nello stesso senso e in direzione opposta alla rotazione giornaliera. Così, il moto apparente del pianeta P è la risultante di due componenti: il moto del pianeta sul suo epiciclo e il moto del centro di questo epiciclo sul deferente. Il periodo del moto del centro dell’epiciclo sul deferente è l’anno solare, che secondo Vitruvio è più breve del periodo del moto del pianeta sull’epiciclo nel caso di Venere e leggermente più lungo nel caso di Mercurio (ibidem, IX, 1, 8-9).
In che modo l’opinione secondo cui Mercurio e Venere si muovono su epicicli può spiegare le loro apparenti stazioni e retrogradazioni? Vitruvio non lo dice, tuttavia non è difficile individuare un semplice, anche se rudimentale, argomento qualitativo che possa servire a questo scopo: difatti sarebbe stato relativamente semplice per gli Elleni e per i Romani del I sec. a.C. elaborare una spiegazione qualitativa, basata sugli epicicli, per comprendere i fenomeni planetari, anche senza essere in grado di determinare con precisione la collocazione dei punti stazionari o la lunghezza degli archi retrogradi - per non parlare delle relative e appropriate dimensioni dell’epiciclo e del deferente, e così via. L’osservazione è importante perché questo genere di precisazioni compare per la prima volta nel cap. I del Libro XII dell’Almagesto di Tolomeo, in cui, attraverso una dimostrazione geometrica, è determinata la posizione dei punti stazionari.
Dopo aver stabilito che Mercurio e Venere effettuano le loro stazioni e retrogradazioni muovendosi attorno al Sole come intorno a un centro (Tav. VII), Vitruvio prosegue spiegando che ciò può essere osservato facilmente nel caso di Venere, che a volte appare come stella vespertina (Vesperugo) e a volte come stella mattutina (Lucifer: fig. 4). Quindi stabilisce il numero dei giorni necessari al compimento del periodo siderale di ciascuno dei cinque pianeti, e ciò lo conduce all’osservazione secondo cui «quei pianeti che descrivono le loro orbite al di sopra del corso del Sole, soprattutto quando sono nel trigono in cui quello è entrato, smettono di andare avanti, ma retrocedono e restano fermi fino a quando il Sole non sarà passato da questo trigono in un’altra costellazione» (ibidem, IX, 1, 11).
Vitruvio stabilisce dunque una connessione tra la posizione del Sole e la collocazione di ciascun pianeta quando effettua le sue stazioni e le sue retrogradazioni. In particolare, egli afferma che questi fenomeni caratteristici si verificano ogni volta in cui la distanza angolare del pianeta dal Sole è pari a 4 segni zodiacali, vale a dire è pari a 120°, quando entrambi gli oggetti sono osservati dalla Terra (fig. 9).
Secondo alcuni, ricorda Vitruvio, un pianeta effettua stazioni e retrogradazioni perché, quando il Sole si trova a una notevole distanza, il percorso del pianeta non è più illuminato dai raggi solari e così esso rallenta fino a fermarsi. Egli però non condivide questa opinione, considera invece che la luce del Sole sia visibile in ogni punto dell’Universo. A suo sostegno cita il fatto che persino noi vediamo il Sole quando i pianeti effettuano le loro stazioni e retrogradazioni: se il genere umano può vedere il Sole, come pensare che il divino potere e splendore di questi pianeti possa essere offuscato? A questo argomento devozionale aggiunge una sua teoria: partendo dalla premessa che il calore attrae a sé gli oggetti, giunge a sostenere che l’energica intensità del Sole è trasportata dai suoi raggi sotto forma di un triangolo attraendo così i pianeti, inducendo quelli che seguono ad accelerare e quelli che precedono ad arrestare la loro avanzata e a ritornare a esso. Per spiegare il motivo per cui i pianeti retrogradano soltanto quando si trovano alla distanza del quinto segno dal Sole, piuttosto che del secondo o del terzo, Vitruvio afferma che i raggi del Sole attraversano tutto l’Universo sotto la forma di un triangolo equilatero e ciò è alla base della configurazione del Sole e dei pianeti che è responsabile delle stazioni e delle retrogradazioni (il presupposto è che il potere di attrazione del Sole sia più grande ai vertici di questo triangolo). Inoltre, a ulteriore sostegno di questo argomento, egli cita Euripide e afferma che, se i raggi del Sole avessero la forma di una curva piuttosto che di un triangolo, verrebbero bruciate le regioni vicine al Sole piuttosto che quelle che si trovano a una distanza maggiore da esso.
Non è difficile individuare le deficienze della teoria planetaria delle stazioni e delle retrogradazioni esposta da Vitruvio. Uno dei suoi molti errori è quello di presumere che ogni pianeta effettui più di una retrogradazione durante l’anno solare; inoltre, essa non si dimostra molto utile alla comprensione delle stazioni e delle retrogradazioni di Mercurio e di Venere, dato che questi pianeti non sono mai osservati a 120° di distanza dal Sole (questo problema potrebbe in parte derivare dalla vaghezza di Vitruvio nel determinare l’ordine dei pianeti). Occorre però ricordare che Vitruvio non è uno specialista della scienza del cielo, bensì un ingegnere militare e un architetto, che palesemente attinge informazioni da opere di altri autori. Ciononostante, e forse proprio per questa ragione, la sua incursione nel campo della teoria planetaria ha un grande valore: egli, infatti, a differenza di Diodoro e di Cicerone, con la sua testimonianza dimostra che, nel corso del I sec. a.C., gli autori greci e latini erano giunti a considerare i dati relativi alle stazioni e alle retrogradazioni planetarie un problema che esigeva qualcosa di più di una breve chiarificazione riguardo alla correttezza della terminologia.
Vitruvio rivela che, per affrontare questo problema, erano impiegate due strategie. La prima era geometrica e presupponeva un sistema di moti circolari e costanti che servivano a spiegare le stazioni e le retrogradazioni di un pianeta. Egli utilizza questa strategia solamente per quanto riguarda Mercurio e Venere, quando sostiene che questi fenomeni sono causati dalle loro rivoluzioni, senza tuttavia offrire nessuna indicazione sull’argomento al quale si riferisce; non ci sembra lecito desumere che egli pensasse che ciò fosse vero anche per gli altri pianeti, o persino che ritenesse che questi ultimi si muovessero su epicicli. La seconda strategia, che si potrebbe definire cosmologica, si basa invece sul potere naturale del Sole, inteso in senso astrologico. Sarebbe interessante sapere se la prima strategia considerasse le stazioni planetarie fenomeni apparenti; le cose starebbero certamente così, nel caso in cui Vitruvio intendesse affermare che Mercurio e Venere si muovono su epicicli. Per la seconda strategia invece questi fenomeni erano reali. Comunque, entrambe le strategie erano realistiche, nel senso che si proponevano di determinare la posizione dei corpi celesti e i loro effettivi comportamenti; inoltre, come apprendiamo dal De architectura, nessuna delle due strategie era stata ideata o concepita per spiegare nient’altro che questi fenomeni particolari. Vitruvio non dice nulla sulle variazioni delle distanze dei pianeti dalla Terra o sulle variazioni delle dimensioni o della luminosità apparenti subite da alcuni pianeti durante il loro percorso intorno al circolo zodiacale. Inoltre, cosa altrettanto importante, non dice se esistessero elaborazioni quantitative di queste strategie che consentissero di determinare la posizione di un pianeta nella volta celeste in un momento dato.
In conclusione, il progetto destinato a «salvare i fenomeni », e in particolare i fenomeni planetari delle stazioni e delle retrogradazioni, ebbe origine nel I sec. a.C.; nella sua fase iniziale, fu un tentativo di comprendere e di assimilare un piccolo numero di idee elementari, relative al moto planetario, formulate nel contesto dell’astrologia oroscopica, come si evince anche dalle Naturales quaestiones di Seneca. Il progetto era stato ispirato dalla consapevolezza del fatto che queste idee erano in contrasto con l’eternità e la regolarità che per gli Elleni e i Romani erano esemplificate in modo ideale dai corpi celesti. Il problema divenne, in breve, una questione molto discussa nella scienza del cielo ellenica e romana. Per risolverlo emersero due linee sperimentali di approccio: la prima di carattere geometrico e la seconda di carattere cosmologico; è in questo contesto che Gemino, per la prima volta, formulò esplicitamente il progetto in questione, un contesto che egli e altri scrittori - come, per esempio, Plinio il Vecchio (23 d.C.-79) e Seneca - consideravano già completamente acquisito e assimilato e che svilupparono nei modi che erano loro più congeniali. Iniziò così a delinearsi, attraverso l’emergere di un un problema fondamentale trattato nell’Almagesto, lo scenario storico che vide l’elaborazione della teoria planetaria di Tolomeo.
Gemino e la trasmissione delle teorie planetarie babilonesi al mondo ellenico e romano
L’astrologia oroscopica greco-latina è in gran parte un prodotto del I sec. a.C.; in questo periodo, infatti, nei testi greci e latini compaiono per la prima volta gli oroscopi e l’indicazione degli strumenti necessari al loro calcolo, e sono composti trattati che descrivono questa nuova branca del sapere. Essa affonda le sue radici soprattutto nella scienza del cielo babilonese: si tratta di un’invenzione babilonese che gli Elleni e i Romani adattarono ai loro interessi e alle loro inclinazioni. Probabilmente, dunque, questi ultimi giunsero alla comprensione delle stazioni e delle retrogradazioni dei pianeti non attraverso misurazioni e osservazioni eseguite di propria iniziativa, ma grazie alla funzione che questi concetti svolgevano nell’astrologia babilonese, la quale pronosticava il destino degli individui attraverso il ricorso alle configurazioni della volta celeste al momento della nascita.
La trasmissione delle teorie planetarie babilonesi al mondo ellenico e romano nel I sec. a.C. si configura in realtà come un evento all’interno di un processo durato molti secoli. Sia gli Elleni sia i Romani furono, in epoche differenti e in misura diversa, agenti attivi di questo processo di ricezione di informazioni provenienti da una cultura estranea. Il tipo di informazioni che essi assunsero dai Babilonesi e il modo in cui le assimilarono furono determinati, nella maggior parte dei casi, dai loro interessi e dai loro obiettivi, come nel caso dello schema calendaristico contenuto nel succitato papiro Hibeh 27. Gli sforzi compiuti dagli scrittori greco-latini del I sec. a.C. per spiegare le stazioni e le retrogradazioni dei cinque pianeti costituiscono un analogo episodio di appropriazione creativa della scienza celeste mesopotamica, anche se con caratteristiche diverse. Infatti, nell’adattare alle proprie esigenze e ai propri interessi immediati le nuove informazioni sul comportamento dei pianeti derivate dall’astrologia oroscopica, gli autori greco-latini furono costretti a rivedere la propria concezione della scienza celeste e a porsi obiettivi di nuovo genere. Nel caso della spiegazione dei moti planetari, tuttavia, ciò avvenne inizialmente attraverso l’assimilazione di alcuni concetti, per di più di carattere molto generale, la cui origine babilonese non era esplicitamente riconosciuta da parte degli autori greco-latini.
Il quesito da porsi è quindi il seguente: a quale periodo risalgono i primi tentativi degli autori greco-latini di spiegare nei propri termini i dati numerici o uno schema aritmetico apertamente riconosciuti come babilonesi? La questione non è affatto trascurabile, poiché la scienza celeste babilonese era puramente aritmetica e formata principalmente da un corpus di elenchi, strutturati in base a un calendario lunare e a classi distinte di schemi numerici; e il fatto che, con questi mezzi, si fosse in grado di predire il luogo e la data dei fenomeni celesti (in particolare quelli lunari) costituisce uno dei massimi trionfi scientifici del mondo antico. Al contrario, la scienza del cielo greca, come si era venuta delineando a partire dal IV sec. a.C., era di natura eminentemente figurativa e qualitativa. Il suo scopo non era quello di produrre una teoria in grado di determinare le posizioni dei corpi celesti in un qualsiasi momento, bensì quello di rappresentare per mezzo di figure geometriche i cambiamenti di carattere generale osservabili nel cielo, inserendoli in una prospettiva filosofica che privilegiava la comprensione di ciò che le cose sono rispetto a quella di ciò che esse fanno. Tuttavia, l’opera di Tolomeo, redatta verso la fine del II sec. d.C., offre una sintesi di entrambe queste tradizioni: siamo in presenza di una scienza del cielo che non soltanto è in grado di soddisfare i tradizionali requisiti filosofici e cosmologici, ma è anche fondata su una serie di procedure di calcolo molto più rigorose e coerenti rispetto a quella del passato e corredata di tavole che consentono di determinare la posizione dei corpi celesti in un qualsiasi momento. L’opera di Tolomeo, inoltre, comprende regole di carattere generale per l’interpretazione del significato di queste posizioni, in particolare rispetto alle vicende umane, procedendo così nella direzione stabilita molti secoli prima dai Babilonesi.
La trasformazione dell’originaria scienza del cielo greco-latina in una disciplina che si proponeva di raggiungere gli stessi obiettivi della sua progenitrice e rivale babilonese fu il risultato della riflessione e dell’approfondimento del significato che le conoscenze babilonesi venivano ad assumere nell’ambito del mondo greco-latino. Quella che si verificò fu una trasformazione fondamentale dell’idea stessa di scienza del cielo nel mondo greco-latino, un mutamento che servì a definire il contesto intellettuale in cui si colloca il corpus tolemaico. All’interno di questo processo, un momento cruciale fu quello in cui gli Elleni e i Romani cominciarono a percepire le proprie ricerche in modo alternativo rispetto alla scienza babilonese, e forse persino in competizione con questa.
Ipsicle e Manilio sulla durata del giorno
Sebbene molti autori greco-latini anteriori a Tolomeo si servissero nei loro lavori degli schemi aritmetici babilonesi, adattandoli ai propri scopi, solamente tre di essi ne descrissero il funzionamento o il metodo attraverso cui erano elaborati: Ipsicle, Manilio e Gemino. Per una curiosa coincidenza, i primi due autori si occuparono entrambi del problema delle variazioni della durata del giorno e della notte nel corso dell’anno, una questione affrontata anche nello schema aritmetico contenuto nel papiro Hibeh 27.
Di Ipsicle si sa soltanto che visse, probabilmente, dopo Apollonio di Perge (262 ca. - 180 ca.), ammesso che egli sia veramente l’autore del trattato aggiunto come Libro XIV agli Elementi di Euclide e che l’Apollonio di cui si parla in questo libro sia proprio Apollonio di Perge (cap. XIX). In ogni caso, l’Anaphoricus di Ipsicle affronta sul piano quantitativo il problema considerato sul piano qualitativo nei Phaenomena, scritti in un periodo imprecisato tra il III e il I sec. a.C. e attribuito a Euclide. In quest’opera è trasposto in forma geometrica quello che oggi sappiamo essere uno schema babilonese sulla variazione annuale della durata del giorno e della notte (basato sul principio che la loro durata per un giorno dato dipende dal tempo che i 6 corrispondenti segni zodiacali, o segmenti di 30° del circolo zodiacale, impiegano per sorgere). Ipsicle dimostra in modo dettagliato che lo stesso schema può essere utilizzato per calcolare la durata del giorno e della notte in qualsiasi periodo dell’anno e per qualunque località. Egli inizia con la dimostrazione di alcuni teoremi aritmetici, che poi utilizza per quantificare il tempo di levata di ciascun segno per il ‘clima’ di Alessandria - ossia per qualsiasi località in cui il polo nord celeste si trovi a un’altezza sull’orizzonte suppergiù identica a quella corrispondente ad Alessandria -, partendo dal presupposto che il rapporto tra il giorno più lungo e quello più corto sia, per quel ‘clima’, di 7:5.
Sempre a questo proposito, Manilio (inizio del I sec. d.C.) enuncia una serie di regole per stabilire la durata del giorno e della notte durante ciascun ‘mese zodiacale’, ossia nel numero di giorni che il Sole impiega per attraversare un segno zodiacale. Queste regole sono esposte in modo sommario e prive di quella validità universale che Manilio attribuisce loro, ma l’aspetto più interessante è il fatto che egli, a differenza di Ipsicle che espone il suo schema senza specificarne l’origine, rivendica la paternità del metodo proposto. In breve, sia Ipsicle che Manilio si propongono di esporre uno schema aritmetico per la determinazione della durata del giorno e della notte in qualsiasi periodo dell’anno, ma nessuno dei due riconosce l’origine babilonese delle proprie informazioni. Inoltre, né Ipsicle né Manilio si curano d’inserire le proprie descrizioni all’interno del più ampio contesto della teoria astronomica greco-latina; e nessuno dei due spiega perché i risultati derivanti dall’applicazione degli schemi indicati debbano essere considerati come elementi costitutivi della conoscenza scientifica del cielo.
Il capitolo XVIII dell’Introductio astronomiae di Gemino: l’exeligmós
Il cap. XVIII dell’Introductio astronomiae di Gemino è il primo testo greco-latino che tenti di spiegare, facendolo proprio, uno schema aritmetico di cui è riconosciuta l’origine babilonese. Com’è ovvio, si tratta soltanto di un riconoscimento implicito: infatti, è possibile che quando Gemino afferma che i parametri di cui si serve sono frutto di osservazioni, si riferisca in realtà a qualcun altro. Comunque questo dimostrerebbe che lo schema, di cui ci è nota l’origine babilonese, era già stato assimilato in qualche modo dalla cultura greco-latina. Gemino analizza il moto della Luna ‘in longitudine’, ossia il suo moto nella direzione del moto annuale del Sole, misurato in gradi lungo l’eclittica: la sua esposizione si differenzia da quelle di Ipsicle e di Manilio non soltanto per l’argomento, ma anche perché in essa l’autore presenta uno schema aritmetico caldeo (cioè, babilonese) in modo tale da comprovarne la validità.
Come spiega Gemino, si può osservare la Luna descrivere lungo l’eclittica archi di diversa amplitudine, che variano di giorno in giorno (la misura di questo arco è detta ‘moto diurno’): essi aumentano da un minimo fino a un massimo, per diminuire poi di nuovo fino al minimo. Il ciclo corrispondente a questo moto longitudinale non uniforme della Luna è il ritorno lunare: un ‘ritorno lunare’ - o ‘mese anomalistico’, nella terminologia moderna - è il periodo che intercorre fra due archi diurni minimi. Il moto della Luna era stato osservato accuratamente dai Babilonesi, i quali raccoglievano i loro dati in tavole astronomiche che indicavano la distanza angolare in longitudine percorsa ogni giorno dalla Luna lungo l’eclittica. Nel sito dell’antica Uruk, in Mesopotamia (l’attuale Warka irachena), gli scavi archeologici moderni hanno riportato alla luce alcune tavole di questo genere, che consistono unicamente di colonne di numeri, senza che si sia conservato nulla che possa servire per spiegarle. Il contributo di Gemino fornisce un tentativo di chiarificazione dei principî e dei parametri aritmetici su cui si basavano questo tipo di tavole.
Gemino apre il capitolo - nella versione in cui la sua opera ci è giunta - con la descrizione dell’exeligmós, vale a dire, del più breve intervallo di tempo contenente un numero intero di giorni, di mesi (sinodici) e di ritorni lunari (un mese sinodico è il periodo compreso tra una ‘congiunzione’ - quando il Sole e la Luna si trovano alla stessa longitudine sull’eclittica - e quella successiva, o tra una ‘opposizione’ - o Luna piena - e quella successiva). Egli afferma che è stato osservato che la durata di un mese sinodico è di quasi 29;2,33 (=29,042500) giorni e la durata di un ritorno lunare, o ‘mese anomalistico’, è di quasi 27;2,18 (=27,038333) giorni; inoltre, sempre in base alle osservazioni, l’exeligmós risulta composto da 669 mesi (sinodici), ossia 19.756 giorni, ossia 717 ritorni lunari (mesi anomalistici), ossia 723 rivoluzioni zodiacali della Luna, più 32°. Questi fenomeni, afferma Gemino, studiati da lungo tempo, erano ampiamente conosciuti. Rimaneva invece da determinare quella che egli chiama «l’irregolarità dell’arco diurno della Luna». Di conseguenza, il problema fondamentale del cap. XVIII è la determinazione del moto diurno minimo (m), del moto diurno massimo (M) e del moto medio (μ) della Luna, e della quantità costante che viene ad aggiungersi o a sottrarsi ogni giorno a questi archi (d). A questo proposito Gemino ricorda che, secondo le osservazioni, 11°/g<m<12°/g e 15°/g<M<16°/g.
A partire dal valore dell’exeligmós Gemino calcola il moto medio (periodico) della Luna: μ=(723x360°+32°)/19.756=13;10,35 (=13,176389)°/g (ma su questo calcolo di Gemino, che non è preciso, v. oltre). Come riconosce lo stesso Gemino, questo calcolo era stato eseguito per la prima volta dai Caldei, già associati in questo trattato all’astrologia. È probabile quindi che tutti i valori introdotti derivati dall’osservazione, fossero già noti ai Caldei, i quali erano stati forse proprio i primi a osservarli. La domanda che si pone è: quali sono i valori di m e M? Gemino inizia col calcolare che la durata media di un mese anomalistico (P) è di 27;33,20 (=27,555...) giorni; per ottenerlo basta dividere i 19.756 giorni dell’exeligmós per il corrispondenti 717 ritorni lunari o mesi anomalistici: P=19.756/717=27;33,20 (=27,555...) giorni (ma di nuovo qui vi è un errore di calcolo di Gemino, il quale fornisce un valore che corrisponde al valore osservativo prima menzionato, cioè 27;2,18 (=27,038333) giorni : v. oltre). Di seguito Gemino divide P in quattro sottointervalli uguali definiti dai moti diurni minimo, medio e massimo, ossia in modo tale che I(m,μ)=I(μ,M)=I(M,μ)=I(μ,m)=6;53,20 (=6,888...) giorni, dove, per esempio, I(m,μ) è l’intervallo compreso tra il giorno in cui la Luna effettua il suo moto minimo (arco minimo) e quello in cui effettua il suo moto medio (arco medio o aritmetico). Quindi, afferma Gemino, poiché il moto diurno medio della Luna è di 13;10,35°/g (=13,176388)°/g, dall’uguaglianza μ=(M+m)/2=13;10,35°/g segue che M+m=26;21,10 (=26,352778)°/g. Si osservi che in questo passaggio Gemino identifica il moto medio periodico con il moto medio aritmetico, confondendo due quantità che forniscono valori medi mediante calcoli diversi.
Tuttavia, la somma dei moti minimo e massimo è, in base all’osservazione, di soli 26°, e, di conseguenza, la parte frazionaria del valore dato poco sopra per M+m, ossia 0;21,10 (=0,352778)°/g, sembra sfuggire all’osservazione strumentale. Questo significa che, per trovare M e m, bisogna assegnare loro 0;21,10°/g, in modo tale che siano soddisfatte le seguenti tre condizioni (si ricordino i limiti superiori dei valori di M e m dedotti dalle osservazioni prima citati): (M+m)=26;21,10°/g, m≯12°/g e M≯16°/g.
A questo scopo, prima di tutto Gemino osserva che, in ciascuno dei quattro sottointervalli in cui ha diviso il mese anomalistico, la differenza d che viene ad aggiungersi o a sottrarsi giornalmente all’arco è costante. Questo comporta, osserva ancora Gemino, che è necessario trovare un valore d (in gradi al giorno) tale che dx6;53,2(=dx6,883889)=k°/g, dove k è il moto complessivo della Luna durante ciascuno dei quattro sottointervalli del mese anomalistico; tenendo presente la divisione del mese anomalistico, si ha M=μ+k e m=μ-k, e pertanto le condizioni che devono essere soddisfatte si possono esprimere nel modo seguente:
[1] 11°<(μ-k)<12°, 15°<(μ+k)<16°,
[(μ-k)-11°]+[(μ+k)-15°]=0;21,10 (=0,352778)°.
Il valore di d, afferma poi perentoriamente Gemino, è di 0;18°/g. Infatti, con i valori d = 0,18°/g e μ=13;10,35°/g, allora k=0,18°/gx6;53,20 g=2;4°; di conseguenza, si ottengono i seguenti valori per i moti diurni massimo e minimo:
M=(μ+k)=13;10,35+2;4=15;14,35 (=15,243055)°/g,
m=(m-k)=13;10,35-2,4=11;6,35 (=11,109972)°/g.
Alcune incongruenze contenute nella dimostrazione di Gemino
La spiegazione dell’exeligmós di Gemino contiene numerose incongruenze. Prima di tutto, occorre notare che l’exeligmós non è il ciclo più breve del suo genere, come si riteneva all’epoca di Gemino: esiste infatti un altro ciclo babilonese, il sáros, che è più corto. Il sáros corrisponde a un periodo di 223 mesi sinodici, durante il quale la Luna completa 239 ritorni lunari e percorre il circolo zodiacale per 241 volte, più 10;30 (=10,5)°; il sáros comprende 6585;20 (=6585,333...) giorni. Ciò che rende il ciclo di sáros particolarmente interessante è il fatto che in questi 223 mesi sinodici la Luna nuova (o piena) ritorna per 242 volte nella stessa posizione in rapporto allo stesso ‘nodo’ (il punto in cui l’orbita lunare interseca l’eclittica); in altre parole, questo ciclo contiene anche 242 mesi draconici.
È certo che il ciclo di sáros era noto in qualche forma agli autori greco-latini dell’epoca di Gemino. Il suo contemporaneo Plinio il Vecchio, nella Naturalis historia, afferma che le eclissi ricorrono secondo un ciclo di 223 mesi (le eclissi si verificano quando la Luna attraversa un nodo o si trova nelle sue vicinanze). La Introductio astronomiae, invece, è il primo testo greco o latino, tra quelli che ci sono pervenuti, che descrive l’exeligmós, un ciclo tre volte più lungo del sáros, senza fare tuttavia alcun accenno alla possibilità di servirsene per prevedere le eclissi. Gemino, infatti, non collega mai esplicitamente l’exeligmós con le eclissi e non menziona la relazione, di importanza fondamentale, tra 669 (=3x223) mesi sinodici e 726 (=3x242) mesi draconici. Si dovrà attendere Tolomeo per trovare la prima trattazione completa dell’exeligmós nella letteratura astronomica greco-latina (Syntaxis mathematica, IV, 2). In secondo luogo, il tentativo di Gemino di quantificare la differenza d che viene ad aggiungersi o a sottrarsi giornalmente al moto diurno della Luna è insoddisfacente anche perché dalle condizioni [1] relative al valore k nell’analisi prima descritta non si può dedurre un valore preciso, bensì una gamma di valori per k, M e m, in cui rientrano anche quelli indicati da Gemino. Si può sospettare, quindi, che egli fosse già in possesso dei valori dei moti diurni minimo e massimo m e M, oltre a quello di d, ma non avesse compreso che d dipende dalla durata media P del mese anomalistico e dalla differenza Δ=(M-m) tra il moto diurno massimo e quello minimo. In altri termini, Gemino conosceva i valori di d, m e M, ma non sapeva che d=2Δ/P=2x4;8°/(27; 33,20 g)=0;18 (=0,3)°/g.
Infine, si devono considerare attentamente alcune questioni relative ai calcoli eseguiti per giungere alle relazioni date in precedenza. Il valore esatto del moto medio diurno periodico è 13;10,34,51,55… (=13,176351)°/g, e non 13;10,35 (=13,176388)°/g, come nella formula data prima per m; la differenza è trascurabile, ed è possibile che Gemino abbia semplicemente arrotondato il risultato. Per quanto riguarda il calcolo di P, invece, il problema non è altrettanto facilmente risolvibile, poiché 19.756/717=27; 33, 13,18, 19…(=27,553695) giorni, e non 27;33,20 (=27,555...) giorni. Si potrebbe supporre che Gemino non fosse un grande esperto di matematica e che si sia accontentato di questo risultato. Oppure, seguendo Neugebauer, si potrebbe pensare che, in questo caso, egli abbia tentato di conciliare due diverse tradizioni babilonesi, la prima risalente agli schemi sul moto lunare di Uruk, nei quali è assegnata al mese anomalistico P una durata di 27;33,20 (=27,555...) giorni, riportata prima, e l’altra proveniente dai testi babilonesi sul ciclo di sáros, nei quali la durata del mese anomalistico è invece di 27;33,13,18,19… (=27,553695) giorni (per ottenerlo basta dividere i 6585;20 (=6585,333...) giorni del sáros per i corrispondenti 239 ritorni lunari o mesi anomalistici).
In realtà, è preferibile interpretare questa discordanza nel valore di P come una variante di un calcolo che parte dal numero di giorni contenuto in un exeligmós e lo divide per il valore del mese anomalistico medio osservato che Gemino ha indicato all’inizio del capitolo (27;33,20=27,550555... giorni), per ottenere il numero di mesi anomalistici o ritorni lunari contenuti in un exeligmós. Ciò equivale a ritenere che il calcolo di partenza di Gemino fosse 19.756/(27;33, 20)=717 ritorni lunari e che la relazione ora data servisse a garantire l’esattezza del calcolo eseguito con la relazione data prima. A sostegno di questa interpretazione, si può notare come sia possibile ricavare con lo stesso procedimento anche il numero dei mesi sinodici da quello dei giorni contenuti in un exeligmós e dal valore del mese sinodico medio osservato, fornito pure da Gemino (29;31,49,5=29,518259 giorni): 19.756/(29;31,49,5)= 669;0,27…= 669 mesi sinodici.
Comunque, la dimostrazione inoppugnabile che questo fosse effettivamente il modo in cui Gemino considerava i suoi dati è fornita dal valore che egli assegna al moto zodiacale (o siderale) della Luna durante un exeligmós. Nei testi babilonesi sul ciclo di sáros che ci sono pervenuti, come si è visto, è indicato che nei 223 mesi sinodici di un sáros la Luna effettua 241 rivoluzioni zodiacali più 10;30° (=10,5°) Curiosamente, il valore indicato da Gemino è diverso: secondo lui, infatti, la Luna effettua 241 rivoluzioni zodiacali più 10;40° (=10,666...°) in 223 mesi sinodici, ossia in un terzo di un exeligmós (v. sopra). Tale stranezza può essere spiegata se si parte dal presupposto che il valore del moto zodiacale della Luna sia stato ottenuto da Gemino dividendo il numero di giorni in un exeligmós per il valore che egli fornisce (si tratta di un dato di osservazione) per l’anno (siderale), 365;4 (=365,066...) giorni, e se s’interpreta correttamente il significato del valore risultante. Infatti, dato che 19.756/(365;15)=54;05,20,19,42,…≈54;05,20(=54,088...) anni e che il Sole descrive in un anno un arco di 360°, ne consegue che, nel corso di un exeligmós, il Sole completa 54 rivoluzioni zodiacali e avanza di altri 32°: infatti, 0;05, 20x360° (=0,088... x360°) = 32°.
Ora, se il Sole fosse una stella fissa, la Luna completerebbe esattamente una rivoluzione zodiacale in un mese sinodico e, di conseguenza, nei 669 mesi sinodici di un exeligmós, completerebbe esattamente 669 rivoluzioni zodiacali. Come Gemino ben sa, però, il Sole è dotato di un moto proprio diretto in senso opposto alla rotazione diurna delle stelle fisse. Questo significa che, per raggiungere il Sole, la Luna deve percorrere più di 360° da una congiunzione (od opposizione) a quella successiva. Ora, dato che un exeligmós contiene un numero intero di mesi sinodici, il totale della distanza percorsa dalla Luna in più per raggiungere il Sole equivale alla distanza totale percorsa dal Sole nel corso dello stesso ciclo. Di conseguenza, in un exeligmós, la Luna compie 723 (=669+54) rivoluzioni zodiacali e avanza di altri 32°.
In conclusione, sebbene sia possibile attribuire il citato errore di calcolo all’incompetenza o alla confusione di Gemino, esso potrebbe anche essere interpretato come un indizio di un ragionamento soggiacente, mirato a ricavare il numero dei mesi sinodici e anomalistici, oltre a quello delle rivoluzioni zodiacali, dal rapporto tra il numero dei giorni in questo ciclo e i valori osservativi forniti da Gemino per il mese sinodico medio, il mese anomalistico medio e l’anno (siderale).
Il progetto di Gemino: un nuovo compito per l’astronomia greco-latina
Gemino parte da due classi di dati numerici che egli sostiene siano derivati dall’osservazione: (A) i valori del mese sinodico medio, del mese anomalistico medio, dell’anno (siderale) e il numero di giorni in un exeligmós; (B) il numero di mesi sinodici, di mesi anomalistici o ritorni lunari e di rivoluzioni zodiacali contenuti nell’exeligmós. A questi vanno aggiunti quei valori che non sono stati derivati dall’osservazione (o, almeno, Gemino non lo afferma), cioè il moto diurno massimo della Luna M, il moto diurno minimo m, il moto diurno medio m, la quantità k=(M-m)/4, la differenza d che va ad aggiungersi o a sottrarsi giornalmente all’arco e, infine, i valori reali del moto diurno della Luna nel corso di un mese anomalistico.
È evidente che Gemino ritenga di poter ottenere questi ultimi valori dai dati di osservazione delle classi (A) e (B). Il suo errore nel valutare d, di cui non afferra il legame con il valore della differenza M-m, non ha importanza. Il fatto che egli introduca di proposito limiti derivati dall’osservazione per ridurre la gamma di possibili valori per M e m, e il metodo seguito per determinare m sembrano sufficienti a dimostrare di quale natura fosse il ragionamento che cercava di costruire. Comunque, Gemino organizza anche i dati osservativi derivando quelli della classe (B) da quelli della classe (A). In sostanza, dunque, il procedimento seguito per spiegare l’exeligmós consiste nello specificare i principali parametri derivati dall’osservazione, nel ricavare da essi altri parametri osservabili, e infine nel dedurre altri dati numerici relativi al moto della Luna nel corso di un mese anomalistico. Lo scopo di Gemino era quello di organizzare le informazioni numeriche riguardanti l’exeligmós in accordo con i criteri correnti di razionalità. Più precisamente, la sua ricostruzione potrebbe essere fondata sul presupposto secondo cui una teoria astronomica è valida quando è il frutto di una deduzione matematica effettuata a partire da alcuni parametri fondamentali, derivati dall’osservazione.
Ora, prescindendo dal fatto che i parametri fondamentali utilizzati da Gemino possano differire in qualche dettaglio da quelli ipotizzati, non c’è dubbio che la sua esposizione dell’exeligmós sia profondamente diversa dalla ricostruzione grafica moderna. Infatti, mentre quest’ultima non asserisce nulla riguardo ai rapporti tra i dati tabulari contenuti nello schema di Uruk e il reale moto della Luna, l’analisi di Gemino, fondata, come si è visto, su affermazioni riguardanti ciò che si presume sia stato osservato del comportamento della Luna, spinge il lettore a credere che le distanze percorse giornalmente dalla Luna siano realmente comprese tra due estremi e varino in misura costante, mediante l’aggiunta o la sottrazione di una quantità fissa. Le conseguenze di tutto ciò, sia per il trattato di Gemino sia per la successiva storia dell’astronomia, sono di grande rilievo.
Considerato in rapporto al trattato nel suo insieme, l’argomento contenuto nel cap. XVIII è un vero disastro. In primo luogo, occorre notare che, qualunque fosse il modo in cui i Caldei (Babilonesi) avevano dedotto e concepito l’exeligmós, Gemino lo ha profondamente frainteso. Si direbbe piuttosto che in questo capitolo egli sia partito difilato nel tentativo d’inserire i dati numerici di origine babilonese in un contesto culturale ad essi estraneo. Nel far questo, egli è stato costretto, però, a sacrificare il proprio progetto, delineato nel cap. I, nel quale, come si è visto, afferma che il compito degli astronomi è quello di spiegare i moti del Sole, della Luna e dei cinque pianeti riconducendoli a una serie di moti circolari e uniformi (v. sopra), e fornisce perfino un esempio di ciò che intendeva dire, attribuendo la diversità delle stagioni astronomiche, definite dai solstizi e dagli equinozi, all’eccentricità dell’orbita circolare su cui il Sole si muove a velocità costante. Considerata sotto questo profilo, l’analisi del moto lunare contenuta nel cap. XVIII è incompleta, dato che Gemino si limita a descrivere il moto apparente della Luna e resta debitore verso i lettori della spiegazione di come questo moto apparente possa essere ricondotto a una serie di moti reali, rispondenti ai requisiti descritti nel cap. I. Tuttavia, un’operazione del genere sarebbe stata estremamente difficile, se non impossibile; in poche parole, il trattato di Gemino, così come lo conosciamo, non contiene le risorse necessarie per derivare in modo coerente e unitario la sua ricostruzione aritmetica e schematica del moto lunare apparente da una rappresentazione geometrica del suo moto reale, così come aveva fatto nel cap. I per il Sole. In sostanza, Gemino è costretto a rinunciare al proprio progetto di spiegare i moti apparenti o osservabili dei corpi celesti e di ricondurli ai loro moti reali.
Ciononostante, gli sforzi da lui compiuti nel cap. XVIII rappresentano un notevole contributo allo sviluppo della scienza del cielo greco-latina. In questo capitolo si cristallizza il bisogno di un progetto interamente nuovo, che si serva dei parametri derivati dall’osservazione per quantificare dei modelli geometrici, all’interno di una teoria tesa a determinare, mediante procedimenti di tipo geometrico, la posizione di un dato corpo celeste in un qualsiasi momento. Non c’è dubbio che un simile progetto oltrepassasse di molto l’orizzonte di Gemino. Appare particolarmente significativo il fatto che egli, pur ‘derivando’ i valori del moto diurno della Luna da parametri osservativi, non stabilisca mai un’epoca per il moto lunare (un’indicazione cioè dell’istante dal quale convenzionalmente si incomincia a misurare la longitudine della Luna) né dia indicazioni su come determinarla; è a causa di questo, infatti, che l’Introductio astronomiae non contiene informazioni sufficienti a calcolare la posizione della Luna in un determinato giorno, passato o futuro. Inoltre, la realizzazione di un simile progetto avrebbe richiesto un esame critico di alcune questioni fondamentali, che Gemino affronta soltanto parzialmente e di sfuggita. Se si fosse stati davvero convinti - come potrebbe esser stato Gemino - che l’accuratezza di una teoria astronomica è garantita dal suo essere fondata sull’elaborazione matematica di parametri derivati dall’osservazione, sarebbe stato necessario specificare il tipo di osservazioni adeguate e i metodi per eseguirle, per non parlare delle procedure necessarie per derivare da queste i parametri. Ancora: anche se l’idea che il moto della Luna debba essere interpretato come una deviazione regolare o sistematica da un moto medio diurno si rivelò uno strumento valido, era importante decidere in che modo andasse calcolato questo valore medio, evitando di confondere valori aritmetici e valori periodici, come accade invece a Gemino.
In conclusione, nel tentativo di spiegare i dati riguardanti il moto diurno longitudinale della Luna, Gemino fu costretto a rinunciare a un progetto che affondava le sue radici nel I sec. a.C., quando gli autori greci e latini divennero sempre più consapevoli della varietà dei moti descritti dalle stelle erranti o pianeti. Infatti, la spiegazione dello schema lunare contenuta nel suo stesso trattato è chiaramente in contraddizione con l’obiettivo di dar conto dei moti apparenti di questi corpi celesti, riconducendoli a moti reali di tipo circolare e uniforme. Il fallimento di Gemino e le prospettive che esso apriva si articolarono in una serie di questioni del tutto inedite, riguardanti la vecchia distinzione tra reale e apparente, oltre che il problema della natura e del ruolo dell’osservazione e il ruolo dell’argomentazione matematica nella scienza del cielo. Non bisogna dimenticare, tuttavia, che Gemino anticipava anche alcuni strumenti per rispondere a queste domande: le idee che si riveleranno più fertili sono, da una parte, la convinzione che i dati derivati dall’osservazione possono essere strutturati mediante una ricostruzione matematica e, dall’altra, la possibilità di quantificare un moto irregolare come una deviazione regolare da un moto medio.
Tra spiegazione e predizione: le eclissi nel mondo romano
I Greci e i Romani concepivano il passato in un modo che, in una certa misura, consentisse di attenuare l’incertezza del futuro e ritenevano che l’esperienza personale fosse una base sufficiente per formulare alcune previsioni sugli eventi futuri. Non pensavano la stessa cosa, però, a proposito della scienza come sapere razionale, almeno per quanto riguarda il periodo più antico; i testi di scienza greca risalenti al V e al IV sec. a.C. che ci sono pervenuti limitano infatti il ruolo della scienza alla spiegazione dei fenomeni e attribuiscono un’importanza marginale o nulla alla predizione. Infatti, se il compito della scienza è quello di individuare le ragioni o le cause universali dei fenomeni, allora le spiegazioni scientifiche possono concernere il futuro solamente nel senso limitato che gli explananda devono poter essere rappresentati con esempi concreti in ogni momento. Così, Aristotele espone dettagliatamente la sua ben nota spiegazione delle eclissi in numerosi brani dei suoi scritti, ma non dice nulla di specifico riguardo alla previsione del momento del loro verificarsi. Al contrario, l’Almagesto di Tolomeo indica ai suoi lettori gli strumenti matematici necessari per calcolare il momento in cui le eclissi si produrranno, la loro ampiezza, la loro durata e così via. L’Almagesto, infatti, è la prima opera dell’antica astronomia greco-latina in cui l’idea della previsione dei fenomeni celesti è enunciata in maniera esplicita.
Per comprendere quando e per quale ragione l’antica scienza del cielo greco-latina si trasformò in uno strumento che consentiva di prevedere con precisione i fenomeni celesti, è necessario - dal momento che i fenomeni in discussione sono periodici - distinguere la predizione del prodursi di alcuni fenomeni celesti da una generica aspettativa riguardo al naturale ripetersi di tali eventi nel corso del tempo. Una previsione astronomica è una predizione del futuro verificarsi di un fenomeno celeste, espressa nella forma di un enunciato basato su una teoria astronomica riconosciuta o derivato da quest’ultima. L’enunciato deve poter essere considerato parte di questa teoria e, inoltre, deve identificare quanto meno il giorno in cui l’evento celeste si verificherà. Una previsione astronomica dunque, presupponendo una determinata base teorica, produce una ‘osservazione datata’, vale a dire, una segnalazione del verificarsi di un evento celeste in un momento ben determinato. Questa definizione esclude quindi le asserzioni che stabiliscono una correlazione tra il sorgere delle stelle e il verificarsi di fenomeni meteorologici nel corso dell’anno, contenute in numerosi calendari greci e latini pervenutici dall’Antichità. Tali asserzioni, infatti, non sono né datate con precisione - non si riferiscono a un anno preciso - né sono presentate come inferenze dedotte da una ben determinata teoria astronomica.
Nel seguito rivolgiamo la nostra attenzione a un fenomeno specifico, le eclissi solari e lunari. Occorre determinare quando, perché e in quale contesto, gli astronomi ellenici e romani iniziarono a interessarsi alla loro previsione. Dal momento che l’Almagesto di Tolomeo è la più antica opera tecnica, tra quelle greche e latine che ci sono pervenute, ad affermare esplicitamente che la previsione delle eclissi è uno dei compiti dell’astronomo, possiamo far riferimento a un preciso terminus ante quem; tuttavia, per individuare il terminus post quem è necessario rivolgersi al corpus dei documenti letterari che ci sono pervenuti, poiché non vi è nessuna prova certa (esplicita o implicita) che attesti questa idea nei documenti tecnici più antichi della scienza del cielo greco-latina.
I primi riferimenti alla previsione delle eclissi
Secondo un’autorevole tradizione interpretativa, la prima fonte letteraria in cui si trova un riferimento alla previsione di un’eclissi è il celebre racconto di Erodoto (490_480-424 ca.) su Talete (VI sec. a.C.) e sul suo intervento in una battaglia tra Medi e Lidi:
In seguito, poiché Aliatte non consegnava gli Sciti a Ciassare che li reclamava, tra i Lidi e i Medi ci fu guerra per cinque anni, e in questi anni spesso i Medi sconfiggevano i Lidi, spesso i Lidi sconfiggevano i Medi; una volta combatterono una battaglia di notte. Mentre combattevano con uguale fortuna, nel sesto anno durante uno scontro accadde che in pieno combattimento il giorno all’improvviso divenisse notte. Un tale cambiamento del giorno era stato preannunciato agli Ioni da Talete, indicando l’anno in cui il fenomeno avvenne davvero. I Lidi e i Medi, quando videro il giorno farsi notte, smisero di combattere ed entrambi si adoperarono di più perché si facesse la pace. (Erodoto, Historiae, I, 74)
Il credito che questa tradizione concede al riferimento di Erodoto è eccessivo, poiché esso non è sufficientemente preciso: in primo luogo, non si può affermare con certezza che si riferisca effettivamente a un’eclissi (l’autore non dice nulla sulle cause che avevano provocato l’oscuramento del cielo e omette il riferimento al terrore dei testimoni, generalmente presente in tutti i resoconti letterari più tardi delle eclissi); in secondo luogo, anche ammettendo che la causa dell’oscuramento fosse un’eclissi, il racconto è ambiguo. Da un lato, esso potrebbe voler dire che Talete l’aveva prevista specificando l’anno in cui si sarebbe prodotta, dall’altro, potrebbe significare che egli l’aveva spiegata precisando che tali fenomeni avevano luogo soltanto in determinati momenti del percorso annuale del Sole, quando, cioè, le sue congiunzioni con la Luna soddisfano certe condizioni; le due alternative sono ugualmente problematiche e nella letteratura antica del periodo successivo a Erodoto si fa riferimento a entrambe. Infine, non è necessario pensare che si trattasse di un’eclissi: se invece la causa dell’oscuramento fosse stata una perturbazione atmosferica stagionale, il racconto di Erodoto potrebbe voler dire che Talete l’aveva prevista - forse basandosi su un almanacco annuale che metteva in correlazione fenomeni stellari e meteorologici, del genere di quelli a cui si fa riferimento nella letteratura dell’epoca di Erodoto - o che l’avesse spiegata come un evento ricorrente nel corso dell’anno. Tutte queste ipotesi, inoltre, danno per scontato un fatto non certo, cioè che il fenomeno osservato dagli eserciti rivali fosse lo stesso preannunciato da Talete agli Ioni. Dunque, il brano delle Storie di Erodoto in cui si fa riferimento a Talete non costituisce una valida testimonianza di una previsione astronomica e, tanto meno, del fatto che previsioni di questo genere fossero un compito degli astronomi.
La prima fonte letteraria greca o latina in cui la previsione delle eclissi è considerata un’attività di competenza degli astronomi risale invece al I sec. d.C.: si tratta del Libro II della Naturalis historia di Plinio il Vecchio, nel quale si loda Ipparco per l’abilità dimostrata nel prevedere le eclissi durante un periodo di seicento anni, sulla base di una teoria astronomica. Prendendo alla lettera questo racconto, si potrebbe far risalire il terminus post quem a Ipparco, ma non si ha nessuna prova diretta, risalente a quel periodo, che possa servire a confermare o a negare le affermazioni di Plinio. Bisogna infatti tenere conto della fama dell’opera In Arati et Eudoxi Phaenomena commentariorum libri tres di Ipparco, nel genere letterario degli Aratea, e della sua elevata statura di autore scientifico. Di conseguenza, è ugualmente possibile che Plinio si riferisca a una procedura babilonese che serviva a determinare il percorso compiuto giornalmente dalla Luna lungo un periodo di seicento anni, o che egli l’attribuisca a Ipparco basandosi sui suoi riferimenti alle eclissi e alle predizioni.
Qui, di nuovo, ci rifiutiamo di cedere alla duplice sollecitazione della tradizione interpretativa secondo cui bisogna valutare gli antichi testimonia soprattutto in termini di veridicità e falsità, e giungere a un verdetto anche nei casi in cui non è possibile formularlo in modo oculato attraverso il ricorso alle prove documentali che risalgono al periodo in questione. Quel che ci interessa è di indagare i motivi che condussero Plinio a riferirsi in quei termini a Ipparco. A questo proposito, bisogna innanzi tutto osservare che il brano di Plinio si apre con il racconto di una versione di una storia singolare, frequentemente narrata dagli autori antichi, quella cioè di Gaio Sulpicio Gallo e dell’eclissi lunare che, a quanto sembra, si produsse durante una battaglia svoltasi nel 167 a.C. nei pressi di Pidna. Secondo Plinio, in questa occasione i Romani, grazie alla spiegazione di Gallo, compresero per la prima volta le cause naturali delle eclissi solari e lunari. La battaglia di Pidna ebbe una grande importanza storica perché segnò la fine della Terza guerra macedone, con la quale, in seguito alla vittoria di Lucio Emilio Paolo su Perseo (primogenito di Filippo V e alleato di Annibale), la Macedonia cedette come potenza mondiale di fronte all’espansione di Roma e, successivamente, fu divisa dai Romani in quattro repubbliche tributarie. Non è quindi sorprendente che gli autori greci e latini la considerassero un momento decisivo dell’ascesa di Roma e del declino del mondo greco e che gli eventi verificatisi in questa circostanza siano stati esaminati in diversi resoconti letterari e storici.
Particolarmente significativo è il racconto del ruolo svolto da Gallo in questa battaglia nella narrazione di Tito Livio (59-17). Si tratta infatti del brano più antico, tra quelli greci e latini che ci sono pervenuti, contenente un riferimento a una previsione astronomica che risponde ai nostri criteri, quella di un’eclissi di Luna. Livio è una delle fonti riconosciute di Plinio il Vecchio e l’analisi del suo racconto è il punto di partenza che permetterà di capire meglio il riferimento di Plinio a Gallo e il contesto culturale nel quale Plinio formulò esplicitamente l’idea secondo cui spetta agli astronomi il compito di prevedere le eclissi.
Secondo Livio,
dopo che i Romani ebbero compiute le difese dei propri accampamenti, Gaio Sulpicio Gallo, tribuno militare della seconda legione e pretore dell’anno avanti, convocati i soldati a parlamento con il permesso del console, dichiarò che nella notte successiva, a scanso di interpretazioni superstiziose del fenomeno, dall’ora seconda all’ora quarta di notte sarebbe venuta a mancare la Luna. Poiché questo fatto si ripeteva a data fissa per legge di Natura, poteva conoscersi in anticipo ed essere preannunziato. Pertanto, come non si stupivano, perché sono fissi tanto del Sole come della Luna il sorgere e il tramontare, che a volte la Luna risplendesse nella pienezza della sua sfera, a volte con un piccolo spicchio quando s’avvia a venir meno, così non dovevano prendere per un prodigio neppure che non potesse osservarsi, quando è celata dall’ombra della Terra. Nella notte sulla vigilia delle none di settembre, all’ora prevista essendosi verificata l’eclissi lunare, ai soldati romani la sapienza di Gallo parve poco meno che divina; mentre lo stesso fatto, come triste prodigio preannunziante la fine del regno e la rovina del popolo, scosse i Macedoni, e allo stesso modo gli indovini. Grida e ululati rintronarono nel campo macedone, sinché la Luna non riapparve nella sua luce. (Tito Livio, Ab urbe condita, XLIV, 37.5-9)
Livio, dunque, riferisce che Gallo, basandosi su una teoria astronomica, avrebbe preannunciato che nel corso della notte successiva si sarebbe verificata un’eclissi lunare. Non vi è alcuna ragione di escludere in partenza la possibilità storica che qualcuno, a quel tempo, fosse in grado di formulare una previsione astronomica del genere di quella che Livio attribuisce a Gallo. Come suggerisce l’analogia tra le fasi lunari e le eclissi, la predizione in questione potrebbe essere stata formulata sulla base di un semplice ciclo astronomico. Ai tempi di Livio infatti, gli scrittori greci e latini conoscevano i cicli delle eclissi, che erano tutti di origine babilonese (come il saros) e che avrebbero potuto certamente essere adattati allo scopo indicato da Livio, anche se con un diverso grado di difficoltà e, a lungo periodo, con scarso successo. Diodoro, sempre nel I sec. a.C., loda l’abilità dei Babilonesi nel predire le eclissi. Questo non significa che all’epoca di Livio, o nel secolo precedente, fosse una pratica comune usare questi cicli per predire le eclissi. Comunque Livio riteneva, a ragione, che questi ultimi potessero essere usati a questo scopo. Il resoconto di Livio è sorprendentemente accurato nei dettagli. La precisione quantitativa con cui sono riportati i dati non ha precedenti tra le numerose versioni della storia di Gallo che ci sono pervenute. Nel contempo, questo è anche l’unico brano in cui Livio indichi la durata di un’eclissi calcolandola attraverso le horae temporariae della notte, vale a dire, in dodicesimi dell’intervallo di tempo dal tramonto del Sole all’alba successiva.
Una tale precisione è assente, per esempio, nel suo resoconto dell’eclissi solare verificatasi a Roma nel 189 a.C. e supera ogni aspettativa, considerato in rapporto alle testimonianze contenute nei trattati astronomici greci e latini antecedenti o contemporanei. Ma la vera sorpresa che riserva il racconto di Livio è che alla data indicata, tra il 3 e il 4 settembre del 167 a.C., non si produsse alcuna eclissi; le eclissi, infatti, si verificano in tempo di plenilunio e nel 167 a.C. la Luna era piena il 20 agosto e il 18 settembre. Tuttavia, quell’anno la Luna raggiunse il plenilunio il 21 giugno e, nella notte tra il 21 e il 22 giugno, si produsse un’eclissi lunare che, teoricamente, avrebbe potuto essere osservata da Pidna. Quest’eclissi, che fu totale, non si verificò però tra la seconda e la quarta ora della notte: infatti, se si fa coincidere l’inizio dell’eclissi con il momento in cui la Luna comincia a entrare nel cono di penombra della Terra e il suo termine con il momento in cui ne esce, a Pidna l’eclissi iniziò molto prima del tramonto del Sole e finì all’inizio della sesta ora della notte. Invece, prendendo in considerazione soltanto la fase in cui la Luna è immersa nel cono d’ombra della Terra, l’eclissi iniziò comunque molto prima della seconda ora della notte, ma ebbe fine nel corso della quarta; per quanto riguarda poi la fase in cui la Luna è totalmente oscurata, questa cominciò all’inizio della prima ora della notte e terminò nel corso della seconda.
Si può pensare, allora, che forse gli eventi narrati da Livio si verificarono in effetti tra il 21 e il 22 giugno e che, forse, la data da lui indicata (3-4 settembre del calendario romano pregiuliano) corrisponde nel calendario giuliano (che entrò in vigore nel 46 a.C.) al 21-22 giugno. Purtroppo, però, ciò non è di alcun aiuto, dal momento che Livio precisa che la battaglia, svoltasi il giorno successivo all’eclissi lunare, ebbe luogo in un momento successivo al solstizio d’estate e nel 167 a.C. il Sole raggiunse il punto del solstizio d’estate il 26 giugno giuliano, più di 4 giorni dopo l’eclissi. In altre parole, se il 3-4 settembre del calendario pregiuliano corrisponde al 21-22 giugno del calendario giuliano – ma ciò è molto problematico dato il modo piuttosto confuso col quale si passò dall’uno all’altro dei detti calendari –, allora il 4 settembre non è la data della battaglia; mentre, se il 4 settembre è la data della battaglia, allora non può corrispondere al 21-22 giugno. Quindi, si deve concludere che nel racconto di Livio sono errati non soltanto il dato relativo alla durata dell’eclissi verificatasi a Pidna, ma anche la collocazione cronologica della battaglia; gli elementi chiave della previsione astronomica attribuita a Gallo - la data, il momento e la durata - sono errati o dubbi perché risultano inconciliabili con la cronologia stabilita da Livio.
Come la maggior parte degli storici antichi, Livio non si propone di registrare semplicemente i fatti. La sua grande opera in numerosi libri, Ab urbe condita, è una monumentale storia di Roma, dalla fondazione fino ai suoi tempi, nella quale egli attribuisce una maggiore importanza ai valori letterari, cioè didattici ed etici, della narrazione che alla sua effettiva accuratezza. Il brano in cui Livio si riferisce a Gallo, e quindi anche quello di Plinio il Vecchio, non devono essere interpretati come semplici resoconti di fatti isolati, ma come osservazioni che acquistano un significato solamente in relazione a uno specifico contesto letterario. Nella letteratura greco-latina, l’idea secondo cui le eclissi sono fenomeni naturali che si ripetono regolarmente in coincidenza di certe configurazioni del Sole, della Luna e della Terra, aveva già una lunga storia ed era usata come antidoto per neutralizzare il terrore provocato in molti dall’opinione secondo cui le eclissi erano presagi o segni di imminenti calamità inviati dagli dèi (al quale si fa riferimento nel Timeo, v. sopra). Tuttavia, essa fu introdotta per la prima volta in un contesto militare da Polibio (200 ca.-120 ca.).
Nelle sue Storie, Polibio introduce in diverse occasioni alcune riflessioni sull’arte del comando militare. Nella più lunga di queste digressioni l’autore espone alcune osservazioni sul valore dell’astronomia e, dopo averne sottolineato l’importanza per ciò che concerne la misurazione del tempo (e quindi per la tempestività, che nell’arte militare è una virtù indispensabile), osserva che un comandante che non vuole rischiare la sconfitta deve sapere che le eclissi non sono presagi di sventura. Polibio, quindi, cita un esempio, la sconfitta subita da Nicia a Siracusa nel 412 a.C.:
Il comandante ateniese Nicia avrebbe potuto salvare il suo esercito a Siracusa; egli aveva già scelto il momento della notte adatto per ritirarsi in luogo sicuro all’insaputa dei nemici, quando sospese la partenza in seguito a un’eclissi di Luna per paura che essa fosse di cattivo auspicio; la notte successiva, mentre tentava di allontanarsi dai suoi, cadde con gli altri comandanti e con tutto l’esercito nelle mani dei nemici che avevano avuto il tempo di conoscere il suo progetto. Se egli si fosse informato tempestivamente presso persone pratiche dei fenomeni celesti, non soltanto non avrebbe lasciato passare il momento favorevole all’azione, ma avrebbe potuto approfittare del timore superstizioso dei suoi avversari. L’ignoranza altrui, infatti, è di grande aiuto a chi ne sappia trarre profitto. (Polibio, Historiae, IX, 19, 1-4)
Purtroppo, Polibio non specifica in quale modo gli esperti dei fenomeni celesti avrebbero spiegato che le eclissi non sono presagi di sventura, o i motivi per i quali egli stesso non avesse timore di interferenze o di presagi divini, benché subito dopo precisi come questo genere di previsioni spettasse agli astronomi piuttosto che ai condottieri. Tuttavia è importante osservare che egli stabilisce una relazione tra l’educazione e la statura di un comandante militare e una certa conoscenza delle eclissi lunari e solari proprio in un’opera in cui sono analizzate le cause del successo dei Romani nell’imporre il loro dominio agli Elleni e alle altre popolazioni del mondo conosciuto. Benché Polibio abbia narrato la battaglia di Pidna nelle sue Storie, di una parte consistente del suo racconto ci sono pervenuti soltanto alcuni frammenti. Uno di questi è contenuto in un lessico del X sec. d.C. che si proponeva di conservare il contenuto del racconto dello storico greco, nel quale l’autore si limita ad affermare che l’eclissi si produsse durante il regno di Perseo e non menziona Gallo.
Diodoro, nel corso della sua discussione sulla scienza del cielo di quelli che definisce i Caldei di Babilonia (v. sopra), osserva che i Caldei, i quali condividevano gli stessi interessi astrologici degli Egizi, consideravano il Cosmo un prodotto della divina provvidenza, non generato ed eterno. Per i Caldei, gli eventi celesti non si producono per caso o spontaneamente, ma in virtù di decisioni ben definite e rigorosamente stabilite dagli dèi; pertanto, le apodosi dei presagi Caldei erano asserzioni relative a eventi futuri che servivano di ammonimento riguardo a ciò che sarebbe accaduto se non fossero stati eseguiti con successo gli appropriati rituali magici. Questo determinismo ha un’importanza decisiva nel caso in cui gli eventi previsti a partire da presagi astrali siano essi stessi astrali, quando cioè l’oggetto della previsione è costituito dalle eclissi lunari e solari. Scrive pertanto Diodoro:
Infatti dicono che [i pianeti] forniscono presagi a quanti sono disposti a prestare loro attenzione, in alcuni casi attraverso il momento della loro levata, in altri attraverso quello del loro tramonto, e in altri ancora attraverso il loro colore. [Dicono], infatti, che a volte [i pianeti] indicano le furie dei venti, e altre volte gli eccessi delle piogge o delle siccità; e in alcuni casi [indicano] l’apparizione delle comete e, inoltre, delle eclissi di Sole e di Luna, oltre ai terremoti e, in genere, tutte le situazioni generate dall’ambiente naturale, che possono essere benefiche o dannose non soltanto per le nazioni e ai luoghi, ma anche per i re e ai semplici cittadini. (Diodoro Siculo, Bibliotheca historica, II, 30.4-5)
Questo brano è piuttosto enigmatico: Diodoro non dice nulla di ciò che costituisce effettivamente la previsione di un’eclissi e non sembra turbato dalla singolarità della tesi secondo cui queste previsioni erano formulate sulla base dell’osservazione dei fenomeni planetari, né dall’implicazione che un’eclissi potesse essere allontanata per mezzo di qualche atto rituale. Tuttavia, dobbiamo notare che l’abilità attribuita ai Caldei non è estesa agli Elleni o, meglio, ai soldati ellenici che considerano le eclissi presagi di sventura. Le osservazioni di Diodoro, inoltre, sono deplorevolmente ambigue anche per quanto riguarda gli Egizi, e in particolare i Tebani; infatti, potrebbero significare che essi consideravano le eclissi segni a partire dai quali predire altri eventi.
In conclusione, Polibio enunciò per primo l’idea che per pervenire al successo un comandante militare deve apprendere attraverso gli insegnamenti degli astronomi che le eclissi non sono segni annunciatori di calamità. Un secolo più tardi, mentre Diodoro spiegava che la previsione delle eclissi era un’importante conoscenza degli astronomi caldei (e forse egizi), Livio, a quanto sembra, utilizzava liberamente queste affermazioni nell’elaborazione della storia delle gesta di Gallo a Pidna.
Cicerone e il valore dell’astronomia
Il resoconto più antico della battaglia di Pidna, con la descrizione dell’eclissi e la storia di Gallo, sembra essere dovuto a Cicerone. Questi, in effetti, menziona sia Gallo sia la battaglia di Pidna in un dialogo filosofico immaginario, il De re publica, ispirato alla Repubblica di Platone, e redatto tra il 53 e il 50. Il protagonista del dialogo - Scipione - rappresenta nell’azione drammatica Publio Cornelio Scipione Emiliano, secondogenito di Lucio Emilio Paolo e intimo amico di Polibio. Benché nelle sezioni introduttive del De re publica Cicerone, parlando in prima persona, indichi le circostanze in cui si svolge il dialogo, che poi riferisce per intero, in realtà il principale interprete delle sue concezioni è Scipione.
Il preciso contesto in cui emerge il riferimento a Gallo e a Pidna è uno scambio di opinioni tra Scipione e Tuberone riguardo alla possibilità di conoscere le cause di fenomeni celesti come la recente apparizione di due Soli, che in breve si trasforma in una discussione sul valore della comprensione del Cosmo in generale e in particolare dell’astronomia. Il problema delle eclissi è menzionato per la prima volta in un passaggio in cui Filo racconta un episodio concernente Gallo e i globi celesti, che quest’ultimo adoperava per mostrare i movimenti del Sole e della Luna e il modo in cui avvengono le eclissi. Subito dopo vi è una lacuna nel testo che ci è pervenuto, e al momento di riassumere Scipione afferma:
Ero io stesso molto affezionato all’uomo che sapevo essere stato stimato e prediletto anche dal padre mio Paolo. Ricordo che essendo ancora giovinetto ed essendo mio padre console in Macedonia e trovandoci noi al campo, tutta l’armata fu d’improvviso presa da un sacro terrore perché nella notte serena, d’improvviso, la Luna candida e piena era scomparsa. E allora lui (Gallo), essendo nostro generale un anno prima all’incirca d’essere eletto console, fu pronto il giorno dopo a spiegare pubblicamente in campo come non ci fosse alcun prodigio e come quello ch’era avvenuto in quel momento e che si sarebbe ripetuto sempre in futuro alla stessa data, fosse dovuto al fatto che il Sole era in un punto in cui non poteva più illuminare la Luna. - Ma è proprio vero? Ma è straordinario! - esclamò Tuberone - Quell’uomo osava spiegare cose simili a gente grossolana e osava dire cose simili a gente assolutamente ignara di tutto - Scipione - proprio così e con una grande… [lacuna nel testo] [Scipione] - nessuna vana ostentazione e nessuna parola indegna d’un uomo tanto serio; e ottenne il più grande successo perché riuscì a liberare quella gente angosciata da un infondato terrore religioso. (Cicerone, De re publica, I, 23-24)
Così, secondo Cicerone, il giorno successivo all’eclissi lunare Gallo rassicurò le truppe offrendo una spiegazione delle sue cause in cui si faceva riferimento alle posizioni relative assunte dal Sole, dalla Luna e dalla Terra e osservando come queste eclissi si verificassero regolarmente nel corso degli eventi celesti e non fossero di cattivo augurio. In effetti, la versione della storia di Gallo nel racconto di Cicerone fornisce molti elementi interessanti. Anzitutto, la teoria astronomica che Cicerone attribuisce a Gallo non è di origine caldea ma ellenica. Benché Diodoro affermi che i Caldei e gli Elleni concordavano nel ritenere che le eclissi lunari si verificavano quando la Luna entra nel cono d’ombra della Terra, egli non attribuisce ai Caldei una teoria analoga per quanto riguarda le eclissi solari. Inoltre, Cicerone era decisamente ostile a quell’astrologia caldea che Diodoro pone in relazione con queste spiegazioni delle cause delle eclissi.
Dal punto di vista di Cicerone, alla divinazione non va riconosciuto uno status di autentica conoscenza ed egli considera divinazione tutta l’astrologia caldea, come sostiene nel suo De divinatione. Cicerone riteneva dunque che la spiegazione dell’eclissi lunare proposta da Gallo fosse di origine ellenica o romana; tuttavia, questa spiegazione si discosta in modo significativo da quelle contenute nel corpus aristotelico perché pone in rilievo l’idea secondo cui le eclissi sono fenomeni naturali che si ripetono regolarmente. In effetti, il resoconto del De re publica individua nella periodicità delle configurazioni dei corpi celesti una componente essenziale della comprensione del fenomeno delle eclissi e apre così la strada all’elaborazione matematica e alla previsione delle eclissi. Ora, è vero che l’idea che le eclissi siano fenomeni periodici e ricorrenti è attestata nella letteratura greca più antica. Tuttavia, è necessario anche precisare che - basandosi su Aristotele - questa periodicità non era affatto considerata di decisiva importanza da tutti. Naturalmente, non è possibile dire se il rilievo attribuito da Cicerone alla periodicità delle eclissi derivi da una riflessione sugli sviluppi della teoria astronomica del suo tempo o se sia un artificio retorico della stessa storia di Gallo. Tenuto conto dello stupore di Tuberone, sembrerebbe infatti che le truppe temessero tutte le eclissi come presagi di sventura e in questo caso Gallo avrebbe potuto rassicurarle soltanto sottolineando la loro periodicità naturale. La versione narrata da Cicerone della storia di Gallo sembrerebbe un adattamento creativo dell’osservazione di Polibio secondo cui un bravo comandante deve sapere che cosa sono le eclissi e che esse non sono presagi di sventura. Per Cicerone, Polibio intendeva affermare che i comandanti devono conoscere la spiegazione causale delle eclissi. Comunque, Cicerone si distingue da Polibio nel sottolineare che l’astronomia rende un grande servizio ed è vantaggiosa per il popolo romano perché racchiude questa conoscenza. Mentre Polibio era disposto a valutare l’astronomia solamente per il suo contributo alle questioni di carattere militare e a pretendere che i futuri comandanti apprendessero l’astronomia soltanto nella misura in cui era utile al loro mestiere, Cicerone tendeva a valorizzarla come scienza. Come afferma esplicitamente, la conoscenza dell’astronomia di Gallo non faceva parte delle cognizioni del comando militare romano e andava molto al di là di ciò che auspica Polibio: questa conoscenza era, invece, un nobile interesse a cui Gallo si dedicava nel tempo libero e che lo distingueva dai suoi pari. In breve, Cicerone considerava l’astronomia come un’occupazione coltivata dai cittadini romani di elevata cultura che poteva influire in modo significativo sul modo in cui essi svolgevano la loro specifica attività, al servizio del popolo romano.
Non c’è alcun dubbio che la conversazione esposta nel De re publica sia un’invenzione letteraria e, anche se ciò non implica necessariamente che anche la storia di Gallo a Pidna sia un’invenzione, questo passo di Cicerone non può essere considerato una prova storica del fatto che Gallo avesse spiegato l’eclissi alle truppe romane atterrite, né della collocazione cronologica dell’eclissi e della battaglia. Come valutare, allora, l’affermazione di Livio secondo cui Gallo aveva predetto l’eclissi? Anche se il racconto di Livio è verosimile (come si è visto, Diodoro aveva divulgato l’idea secondo cui gli astronomi caldei prevedevano le eclissi e spiegavano le eclissi lunari nello stesso modo di quelli greci), è altrettanto possibile che si tratti di una pura invenzione, e non è possibile escludere a priori la possibilità che Livio avesse derivato da Cicerone l’idea secondo cui Gallo aveva predetto l’eclissi lunare osservabile nel 167 a.C. a Pidna.
Nel suo dialogo filosofico De senectute, portato a termine nel 43 a.C., Cicerone integra i suoi precedenti riferimenti a Gallo affermando:
Noi vedevamo Gaio Gallo, intimo amico di tuo padre, o Scipione, struggersi e consumarsi nello sforzo di misurare quasi il cielo e la Terra. Quante volte, avendo cominciato di notte a disegnare qualche figura, fu sorpreso dall’alba, e quante volte, avendo cominciato al mattino, fu sorpreso dalla notte! E come si compiaceva di predirci, molto tempo prima, le eclissi di Sole e di Luna! (Cicerone, De senectute, XIV, 49)
Egli attribuisce dunque a Gallo non soltanto la conoscenza delle cause delle eclissi ma anche la capacità di prevederle. È interessante osservare che, subito dopo aver narrato le gesta di Gallo a Pidna nel De re publica, Cicerone attribuisce le stesse capacità anche a Talete: «Ebbene è fama che sia stato proprio lui a predire per primo l’eclissi solare che si verificò sotto il regno di Astiage» (Cicerone, De divinatione, I, l); è questa la prima attribuzione chiara a Talete nella letteratura greco-latina.
Se i racconti di Cicerone su Gallo costituiscono lo sfondo su cui vengono a collocarsi quelli di Livio, allora bisogna prendere in considerazione la possibilità che Livio, ispirandosi a Polibio, abbia voluto rendere più completa la versione della storia di Gallo narrata da Cicerone, combinando tra loro le affermazioni di Cicerone su Gallo e sull’eclissi, situando la battaglia nel giorno successivo all’eclissi e aggiungendo, per intensificare l’effetto della narrazione, alcuni dettagli riguardo all’eclissi stessa provenienti da altre fonti. Probabilmente egli intendeva rielaborare i riferimenti a Gallo e a Talete contenuti negli scritti di Cicerone e indicare un’ulteriore ragione della vittoria dei Romani sui Macedoni a Pidna, inserendo così nella storia di Gallo un interessante motivo polemico. In questo modo, il mutamento nella concezione dell’astronomia greco-latina che porta a considerare la previsione delle eclissi come uno dei suoi obiettivi potrebbe essere stata una conseguenza accidentale dell’evoluzione dialettica di un topos letterario che affonda le sue radici più profonde nei commenti sul comando militare esposti nel II sec. a.C. da Polibio nelle sue Historiae. Questo topos ricorre in diversi contesti: Cicerone lo utilizza per dimostrare che la conoscenza dell’astronomia può essere utile e vantaggiosa per il popolo romano; Plinio il Vecchio ne estende i benefici a tutta l’umanità; Livio lo adatta alla sua descrizione moralistica e persino polemica della battaglia di Pidna; Valerio Massimo lo presenta come exemplum di discorso pubblico; Marco Fabio Quintiliano (35 ca.-96 ca.) lo cita come esempio del potere benefico dell’oratoria e come prova del valore dell’educazione retorica, e Sesto Giulio Frontino (30 ca.-103/104) come modello di valido comando militare.
Considerando i diversi contesti e i differenti modi in cui è narrata la storia di Gallo, è probabile che il topos debba essere interpretato essenzialmente come un prodotto dell’immaginazione letteraria. La storia ha una base reale, ma questa base sembra in realtà piuttosto fragile: a Pidna si svolse una battaglia nel corso della quale i Romani sconfissero i Macedoni. Nello stesso anno si produsse un’eclissi di Luna osservabile da quel luogo, e a quel tempo Sulpicio Gallo era vivo. La veridicità di ciascuna di queste asserzioni, tuttavia, si fonda su motivi indipendenti. Non è facile stabilire se Gallo abbia effettivamente partecipato alla battaglia di Pidna e, inoltre, ciò non sarebbe sufficiente a provare che egli avesse previsto l’eclissi o che, successivamente, l’avesse spiegata alle truppe. A questo riguardo disponiamo solamente delle fonti precedentemente esaminate, che forniscono esse stesse valide ragioni di dubitare di entrambe le possibilità.
Plinio il Vecchio e la nuova astronomia predittiva
Il modo in cui Plinio il Vecchio rielabora nella Naturalis historia il racconto su quanto fu fatto da Gallo a Pidna, consente di delineare un momento decisivo nella storia dell’astronomia ellenica e romana. Nel Libro II Plinio si occupa del Sole e della Luna e, dopo aver spiegato le cause naturali delle loro eclissi, affronta la questione della storia di queste spiegazioni ricordando quanto segue:
Il primo uomo di stirpe romana a divulgare l’analisi delle eclissi (di entrambi i tipi) è stato Sulpicio Gallo, che fu collega di Marco Marcello nel consolato, ma, all’epoca, era tribuno militare. Fu lui che liberò dall’apprensione (si era al giorno prima della sconfitta che Emilio Paolo inflisse al re Perseo): di fronte alle truppe riu nite, il suo comandante lo fece parlare e preannunciare l’eclissi; più tardi, egli trattò l’argomento anche in un libro. Ma presso i Greci il primo in assoluto a svolgere indagini fu Talete: al quarto anno della XLVIII Olimpiade predisse l’eclissi solare che si verificò sotto il regno di Aliatte, nell’anno 170 della fondazione di Roma. In seguito, Ipparco ha precisato le eclissi di entrambi gli astri per 600 anni, tenendo conto dei mesi, in quanto variano presso le singole popolazioni, dei giorni, delle ore, della configurazione dei luoghi e della visuale celeste che i popoli hanno: il tempo gli è testimone, egli fu davvero il confidente dei progetti della Natura. Grandiose sovrumane figure, voi che avete scoperto la legge di così grandi divinità e liberato ormai lo spirito infelice dei mortali, che nelle eclissi paventavano il manifestarsi di delitti, o una specie di morte delle stelle - timore che notoriamente provavano anche uno Stesicoro e un Pindaro, sublimi voci poetiche, di fronte al venir meno del Sole - o che, a proposito della Luna, sospettavano influssi di magia nera e perciò le venivano in soccorso con numerose cacofonie - per questo tipo di paura, ignaro del vero motivo, il generale ateniese Nicia non si azzardò a far uscire dal porto la flotta, e così mandò in rovina la potenza di Atene -: onore alla vostra genialità, portavoce del cielo, voi che nell’animo sapete accogliere la natura dell’Universo, scopritori di un ragionare con cui avete superato uomini e dèi! E davvero chi mai, vedendo questa realtà, e i ricorrenti travagli (è questa la definizione che si è voluta coniare) degli astri, non perdonerebbe la fatalità che lo domina per aver creato esseri mortali? (Plinio il Vecchio, Naturalis historia, II, 53-55)
Plinio combina così le letture di Polibio, Cicerone e Livio - tutti citati più volte come fonti nel Libro I - nell’elaborazione della sua opera, nella quale uno dei motivi fondamentali è l’idea che il risultato più elevato delle conquiste umane sia soccorrere l’umanità: citando le sue parole, «essere dio è, per un mortale, aiutare un mortale» (Plinio il Vecchio, Naturalis historia, II, 18). Una forma non trascurabile di quest’opera umanitaria è l’affrancamento dell’umanità dalla paura della morte e dal desiderio della vita dopo la morte. Per Plinio queste emozioni sono nemiche della ragione, prima tra tutte quella che nasce dall’ignoranza e perverte la ragione col culto della religione popolare e con le pratiche della magia e dell’astrologia, che offendono tutte la Natura e impediscono alla ragione un genuino rapporto con essa. Così, Gallo e Talete sono figure straordinarie perché hanno spiegato le cause delle eclissi e consentito di predire una singola eclissi e Ipparco è pressoché divino perché, come sostiene Plinio, ha consentito di predirle per un arco di tempo di 600 anni, e per questo non sarà mai abbastanza elogiato.
Un’innovazione fondamentale introdotta da Plinio consiste nell’aver presupposto che la capacità di spiegare e di prevedere le eclissi appartenesse al patrimonio intellettuale ellenico e romano. Questo è di per sé sufficiente a indicare un notevole allontanamento dal punto di vista di Diodoro; quelle che Diodoro considera cognizioni caldee (e forse egizie), sono assunte da Plinio come parte di un imperativo rivolto a tutti gli Elleni e i Romani, di una missione intellettuale fondata su un esercizio elevato della ragione e presumibilmente compiuta già ai tempi di Ipparco, circa cinquant’anni prima che Diodoro divulgasse le conoscenze caldee (ed egizie). Plinio però si spinge oltre: se Diodoro aveva presentato l’astronomia come una serie di teorie e cognizioni sparse, Plinio suggerisce che le indagini di Talete, di Ipparco e di Gallo siano fondate su una teoria coerente. Egli, infatti, nell’elogiare queste grandiose figure, fa riferimento alla conoscenza delle leggi del Sole e della Luna che ha liberato i mortali dal timore delle eclissi e alla teoria che ha consentito all’uomo di conquistare queste divinità. Inoltre, elabora ciò che Ipparco presumibilmente sapeva sulle condizioni temporali che reggono le interposizioni del Sole, della Luna e della Terra e che causano le eclissi, condizioni che quindi fanno riferimento alla questione della previsione. In tal modo, l’appropriazione di teorie astronomiche straniere da parte di Plinio il Vecchio pone il problema di come integrare, nella scienza del cielo ellenica e romana, i modelli cosmologici-geometrici utilizzati per spiegare le eclissi e l’apparato aritmetico necessario alla loro previsione, vale a dire come arrivare a una comprensione della teoria fisica delle eclissi che nel contempo consenta di calcolarne la data, la zona terrestre di osservabilità e persino, forse, il momento e la durata.
In conclusione, le prove documentali che ci sono pervenute dimostrano che il contributo decisivo alla trasformazione dell’astronomia greco-latina da scienza esplicativa e qualitativa in scienza quantitativa e in grado di predire i fenomeni, provenne da un numero ristretto di scrittori, soprattutto romani, nessuno dei quali era un astronomo. Questi scrittori, infatti, suscitarono e diffusero una forte aspettativa riguardo alle capacità degli astronomi ellenici e romani di predire le posizioni assunte dai corpi celesti, e quindi sollecitarono gli astronomi contemporanei e successivi ad affrontare questi nuovi compiti. Gli scrittori che elaborarono la storia di Gallo e dell’eclissi lunare diedero quindi anche origine all’idea che gli astronomi ellenici e romani dovessero essere in grado di formulare previsioni sul verificarsi delle eclissi, consolidando e confermando l’aspettativa, emergente nella stessa scienza del cielo ellenica e romana, che questa disciplina dovesse a un tempo essere esplicativa e in grado di formulare predizioni.
Bibliografia
Bouché-Leclercq 1899: Bouché-Leclercq, Auguste, L’astrologie grecque, Paris, E. Leroux, 1899.
Bowen 1988: Bowen, Alan C. - Goldstein, Bernard R., Meton of Athens and astronomy in the late fifth century B.C., in: A scientific humanist. Studies in memory of Abraham Sachs, edited by Erle Leichty, Maria de J. Ellis, and Pamela Gerardi, Philadelphia (Pa.), Samuel Noah Kramer Fund, The University Museum, 1988, pp. 39-81.
– 1991a: Bowen, Alan C. - Goldstein, Bernard R., Hipparchus’ treatment of early Greek astronomy. The case of Eudoxus and the length of daytime, “Proceedings of the American philosophical society”, 135, 1991, pp. 233-254.
– 1991b: Science and philosophy in classical Greece, edited by Alan C. Bowen, New York, Garland, 1991.
– 1994: Bowen, Alan C. - Goldstein, Bernard R., Aristarchus, Thales, and Heraclitus on solar eclipses. An astronomical commentary on P. Oxy. 53.3710 cols. 2.33-3.19, “Physis”, 31, 1994, pp. 689-729.
Clagett 1989-95: Clagett, Marshall, Ancient Egyptian science. A source book, Philadelphia (Pa.), American Philosophical Society, 1989-1995, 2 v.
Dreyer 1906: Dreyer, John L.E., History of the planetary systems from Thales to Kepler, Cambridge, Cambridge University Press, 1906.
Duhem 1908: Duhem, Pierre Maurice Marie, Σώζειν τὰ φαινόμενα. Essai sur la notion de théorie physique de Platon à Galilée, Paris, A. Hermann, 1908.
Goldstein 1991: Goldstein, Bernard R. - Bowen, Alan C., The introduction of dated observations and precise measurement in Greek astronomy, “Archive for history of exact sciences”, 43, 1991, pp. 93-132.
– 1997: Goldstein, Bernard R., Saving the phenomena, “Journal for the history of astronomy”, 28, 1997, pp. 1-12.
Grenfell 1906: The Hibeh Papyri, edited by Bernard P. Grenfell and Arthur S. Hunt, London-Boston, Sold at the offices of the Egypt exploration fund, 1906-1955, 2 v.; v. I: Egypt exploration fund. Graeco-Roman branch. no. 7.
Heath 1913: Heath, Thomas L., Aristarchus of Samos, the ancient Copernicus. A history of Greek astronomy to Aristarchus, together with Aristarchus’s Treatise on the sizes and distances of the sun and moon, Oxford, Clarendon Press, 1913.
Hunger 1989: Hunger, Hermann - Pingree, David, MUL.APIN. An astronomical compendium in cuneiform, Horn, F. Berger, 1989.
Jones 1997: Jones, Alexander, Studies in the astronomy of the Roman period: the standard lunar calendar, “Centaurus”, 39, 1997, pp. 1-36.
Lloyd 1984: Lloyd, Geoffrey Ernest Richard, Hellenistic science, in: The Cambridge ancient history, edited by I.E.S. Edwards [et al.], Cambridge- New York, Cambridge University Press, 1970-1998, 13 v.; v. VIII. 1.: The hellenistic world, 2. ed.: 1984, pp. 321-352; 591-598.
– 1987: Lloyd, Geoffrey Ernest Richard, The revolutions of wisdom. Studies in the claims and practice of ancient Greek science, Berkeley (Calif.), University of California Press, 1987.
Neugebauer 1957: Neugebauer, Otto, The exact sciences in antiquity, Providence (R.I.), Brown University Press, 1957 (trad. it: Le scienze esatte nell’antichità, Milano, Feltrinelli, 1974).
– 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin-New York, Springer-Verlag, 1975, 3 v.
– 1983: Neugebauer, Otto, Astronomy and history. Selected essays, New York-Berlin, Springer-Verlag, 1983.
Pannekoek 1961: Pannekoek, Anton, A history of astronomy, London, G. Allen & Unwin, 1961.
Sachs 1988-96: Sachs, Abraham, Astronomical diaries and related texts from Babylonia, completed and edited by Hermann Hunger, Wien, Verlag der Österreichischen Akademie der Wissenschaften, 1988- 1996, 3 v.
Spalinger 1994: Revolutions in time. Studies in ancient Egyptian calendrics, edited by Anthony John Spalinger, San Antonio (Tex.), Van Siclen books, 1994.