Scienza greco-romana. Ottica e teoria della luce
Scienza greco-romana. Ottica e teoria della luce
Ottica e teoria della luce
La moderna ottica fisica ha le sue radici storiche nell'ottica matematica greca; il più ovvio legame tra le due è l'uso della geometria dei raggi come strumento fondamentale di analisi; tuttavia queste evidenti somiglianze nascondono differenze decisive. Innanzitutto, mentre la moderna ottica fisica si occupa essenzialmente della luce, l'ottica antica si occupava per lo più della visione; anzi nella tradizione euclideo-tolemaica la luce era quasi ignorata come argomento di interesse teorico. Inoltre, a differenza dell'ottica moderna, che è suddivisa in campi relativamente autonomi ‒ l'ottica fisica e l'ottica fisiologica, la psicologia della visione, e così via ‒, nell'ottica antica tali distinzioni erano, se non proprio assenti, comunque nebulose. Se è vero che le fonti su cui si basa la nostra conoscenza dell'ottica antica si differenziano di solito per il tipo di approccio, che in alcuni casi è filosofico, in altri medico, in altri ancora matematico, tuttavia non è affatto sicuro che gli antichi studiosi dell'ottica si sentissero vincolati da queste rigide partizioni disciplinari. Galeno (129-199/200), per esempio, nonostante il suo interesse professionale per la medicina, nel De usu partium reputò necessario occuparsi della geometria dei raggi (anche se a un livello piuttosto superficiale), così da completare la sua analisi dell'anatomia e della fisiologia della visione. Analogamente, Tolomeo (100 ca.-178 ca.), sebbene nella sua Ottica facesse grande affidamento sull'analisi dei raggi, si dimostrò profondamente interessato a problemi di psicologia e di fisiologia della visione.
Prima di iniziare ad analizzare gli aspetti più propriamente tecnici dell'ottica matematica e due problemi che i teorici classici dell'ottica sembrano aver considerato significativi, ma marginali ‒ la concentrazione della luce attraverso specchi ustori e la formazione dell'arcobaleno ‒, sarà dunque utile prendere in esame l'ottica intesa nel suo significato più generale e affrontare una serie di problemi relativi alle fonti, alle prospettive interpretative, agli sviluppi concettuali e così via.
Linee generali di sviluppo
Le fonti e la loro interpretazione storica
La nostra conoscenza dello sviluppo dell'ottica nell'Antichità si basa su un gruppo molto limitato di fonti, la cui conservazione fino all'età moderna è il risultato non soltanto di eventi storici fortuiti, ma anche di una selezione consapevole. Secondo Diogene Laerzio (attivo forse verso la metà del III sec. d.C.), Democrito (470/457-360/350) scrisse almeno quattro trattati su questioni di ottica, nessuno dei quali è giunto fino a noi. Analogamente, a Teofrasto (371 ca.-287 ca.), discepolo di Aristotele (384/383-322), si attribuiscono quattro opere di argomento ottico, ma soltanto una, il De sensu, è a tutt'oggi conservata. Esempi del genere si potrebbero moltiplicare, ma già questi mettono in evidenza i due principali problemi che si trova ad affrontare chiunque tenti di ricostruire la storia dell'ottica antica.
Il primo è la scarsità delle fonti, soprattutto di quelle primarie; i lavori di ottica oggi disponibili rappresentano, infatti, una piccola parte rispetto a tutti gli studi su questo argomento prodotti nell'Antichità. Per esempio, nel caso dell'ottica matematica, sono arrivati fino a noi soltanto cinque trattati del periodo che va dal 300 a.C. al 170 d.C. circa: l'Ottica e la Catottrica di Euclide (attivo intorno al 300 a.C. ca.), Sugli specchi ustori di Diocle (180/190 a.C. ca.?), la Catottrica di Erone di Alessandria (I sec. d.C.?) e l'Ottica di Tolomeo. La seconda difficoltà consiste nel fatto che queste opere sono tutte in vario modo problematiche. Soltanto le prime due si sono conservate in greco e la loro autenticità è discussa. Il trattato di Diocle, invece, esiste solamente in arabo e né l'autore né la data sono certi. I restanti due trattati, infine, esistono soltanto in versioni latine medievali: la Catottrica di Erone è stata tradotta dal greco, l'Ottica di Tolomeo da un intermediario arabo. Inoltre, a peggiorare la situazione, la Catottrica di Erone ha subito una significativa riduzione prima di essere tradotta; né è andata meglio all'Ottica di Tolomeo, il cui testo oggi in circolazione manca di tutto il Libro I e della parte conclusiva del Libro V.
Anche le fonti che si occupano di ottica a un livello meno tecnico sono relativamente scarse e quelle che si sono conservate sono cronologicamente distribuite in modo non uniforme, analogamente alle fonti tecniche. Le più antiche, datate dall'inizio del IV alla prima metà del III sec. a.C., comprendono parti dei dialoghi di Platone (in particolare il Timeo), molte opere di Aristotele ‒ le più significative delle quali sono il De anima, il De sensu et sensibili e i Meteorologica ‒ il De sensu di Teofrasto e i Problemata pseudoaristotelici, un'opera compilativa che si è formata nell'arco di numerosi secoli, ma che è stata chiaramente costruita intorno a un originario nucleo peripatetico. Per trovare la successiva fonte importante, il De rerum natura di Tito Lucrezio Caro, dobbiamo saltare al I sec. a.C., e fare un altro salto di circa due secoli per le ultime due fonti, il De usu partium e il De placitis Hippocratis et Platonis di Galeno.
È dunque evidente che la nostra conoscenza dell'evoluzione dell'ottica antica si fonda in gran parte su fonti di seconda o terza mano e ciò pone il problema della dubbia attendibilità di queste fonti, molte delle quali furono composte molto tempo dopo gli eventi di cui trattano. Gran parte di ciò che Diogene Laerzio riferisce a proposito dei presocratici, per esempio, non sembra molto affidabile, in quanto le sue Vite probabilmente furono scritte all'inizio del III sec. d.C., cioè dopo più di sei secoli dai fatti di cui parla. Inoltre molte delle fonti primarie valgono come secondarie, poiché gran parte di quello che sappiamo ‒ o crediamo di sapere ‒ sul pensiero ottico prima della metà del IV sec. a.C. si basa su notizie fornite da Aristotele, al quale, più che l'esattezza storica, interessava sottolineare la superiorità delle proprie teorie rispetto a quelle dei suoi predecessori. Ciò che scelse di dirci su di esse, pertanto, è determinato dall'attinenza con l'argomento in discussione. Lo stesso vale per Galeno, al quale siamo debitori di numerose conoscenze a proposito del pensiero stoico sulla fisiologia e sulla sensazione, ma che non era certo d'accordo con gli stoici, e in particolare con Crisippo (280 ca.-205 ca.), il quale, anzi, fu scelto nel De placitis come bersaglio di una violenta e prolungata polemica. Quale attendibilità, dunque, può avere la testimonianza di fonti come queste? La risposta non è scontata: da un lato, non c'è ragione di credere che Aristotele e Galeno distorcessero di proposito le opinioni dei loro predecessori; dall'altro, nel presentarle selettivamente e fuori dal loro contesto, i due pensatori si attenevano a precise necessità retoriche, non storiche.
Sebbene non esaustivo, questo quadro è tuttavia sufficiente a mostrare quanto ogni profilo storico basato su tali fonti e ogni loro interpretazione debbano essere valutati con cautela. Tuttavia, è possibile tracciare alcune linee generali di sviluppo facendo riferimento a tre principali tradizioni di ricerca. La prima di queste può essere definita 'filosofica', nella misura in cui si interessa principalmente dei fondamenti fisici ed epistemologici della visione. All'interno di questa tradizione, era prestata grande attenzione a questioni di causalità fisica: per esempio, cosa distinguesse gli attributi visibili dagli altri attributi sensibili; quale fosse la natura della vista e in che cosa differisse dagli altri sensi; quale tipo di legame potesse essere stabilito tra l'occhio e l'oggetto che conduceva alla percezione visiva, ma non a quella tattile od olfattiva o a tutte le altre sensazioni; infine, quale fosse, in questo legame, l'entità mediatrice. A questo ambito vanno anche ricondotti problemi epistemologici di grande importanza, quali il modo di produzione della conoscenza percettiva e intellettiva a partire dalla sensazione visiva; che cosa significasse 'vedere' caratteristiche fisiche come la forma, la dimensione e così via; quale fosse l'entità mediatrice tra l'impressione visiva e quella percettiva; se la visione potesse essere veridica e, se sì, in quali condizioni. Queste domande furono formulate in vario modo in un periodo di tempo che va tra il 500 a.C. ca. e il 200 d.C., e le prime risposte teoriche (in special modo quelle degli atomisti) facevano leva su principî materiali, mentre le successive ‒ in particolare quelle di Aristotele e degli stoici ‒ propendevano più verso principî qualitativi.
La seconda tradizione di studi può essere definita 'medica' e, nonostante le sovrapposizioni con quella filosofica, se ne distingue per l'attenzione rivolta all'anatomia e alla fisiologia del sistema visivo. Per lo sviluppo di questa seconda tradizione è stata decisiva l'opera dei medici alessandrini Erofilo (intorno al 300 a.C.) ed Erasistrato (attivo intorno al 270 a.C.), nei cui studi pionieristici sull'anatomia dell'occhio e sul sistema nervoso è presente una chiara descrizione dei nervi ottici che collegano gli occhi alla parte anteriore del cervello. Sicuramente fu Erofilo il primo a riconoscere che, diversamente dagli altri nervi sensoriali, i nervi ottici sono cavi; questo fatto suffragava l'idea che attraverso questi nervi, a partire dal cervello fino all'interno degli occhi, scorresse una sorta di effluvio psichico chiamato 'pneuma'. Il successo definitivo di questo modello neurologico fu sancito da Galeno, la cui opera anatomica e fisiologica era fondamentalmente un'elaborazione (pur con sfumature stoiche) di quella dei suoi predecessori alessandrini, in particolare di Erofilo.
Infine, la terza tradizione di ricerca, quella dell'ottica matematica, almeno nelle sue fasi iniziali si occupava essenzialmente dell'analisi dei raggi. Gli albori di questa tradizione sono un po' più oscuri rispetto a quelli delle altre due; è però sicuro che l'uso della geometria dei raggi è precedente ad Aristotele. È possibile, ma tutt'altro che certo, che la teoria dei raggi antica abbia le sue origini nella scenografia (prospettiva) e nel rilievo topografico, che avevano entrambi un approccio estremamente matematico. Comunque, a parte il problema delle origini, non c'è dubbio che, al tempo in cui Euclide compose l'Ottica e la Catottrica, la teoria dei raggi aveva raggiunto un grado di sviluppo piuttosto alto, almeno rispetto ad Aristotele.
Sfortunatamente, la mancanza di testimonianze scritte per il periodo che va da Euclide a Erone di Alessandria rende quasi impossibile seguire la linea di sviluppo dell'ottica fino agli inizi dell'era cristiana; neppure la Catottrica di Erone è molto utile a questo scopo, a causa della sua impostazione sommaria e del suo taglio pratico. Per questa ragione, l'evoluzione dello scenario in cui va collocata l'Ottica di Tolomeo non può essere delineata con sicurezza; essa, però, rappresenta con certezza un grado di sviluppo teorico che è tanto avanzato rispetto a Euclide almeno quanto Euclide lo era rispetto ad Aristotele. Per quanto ne sappiamo, fu Tolomeo a razionalizzare compiutamente lo studio dell'ottica secondo la triplice struttura di ottica propriamente detta (l'analisi della visione diretta), catottrica (l'analisi della riflessione) e diottrica (l'analisi della rifrazione). Tolomeo sembra essere stato un pioniere anche nella verifica sperimentale dei principî ottici, un'innovazione metodologica che condizionò lo studio dell'ottica per tutti i secoli successivi. Inoltre, cosa forse ancora più importante, Tolomeo allargò il campo dell'analisi ottica fino a comprendervi problemi non soltanto matematici, ma anche fisici, fisiologici e psicologici. Il risultato fu una sintesi notevolmente comprensiva e coerente all'interno della quale tutte e tre le tradizioni di ricerca ‒ filosofica, medica e matematica ‒ si trovarono a convergere pienamente.
Modelli fisici della visione
Il modo più semplice per capire le antiche teorie della visione è quello di valutarle nel contesto dei problemi che le hanno generate. Il più importante fra questi riguarda la causalità fisica, ovvero che tipo di relazione esiste fra l'occhio e gli oggetti visibili tale da produrre la visione, e in quale modo essa si stabilisce. È immediatamente chiaro che questa relazione si realizza attraverso un contatto mediato, non diretto; per spiegare questa mediazione, i teorici antichi facevano ricorso a tre ipotesi alternative fondamentali: l''estromissionismo', per cui l'occhio invia qualcosa all'oggetto; l''intromissionismo', per cui l'oggetto invia qualcosa all'occhio; infine una forma mista secondo la quale l'occhio e l'oggetto si raggiungono l'un l'altro.
La più antica tra le teorie intromissioniste sembra essere stata formulata dagli atomisti, che spiegavano il meccanismo della visione in termini materialistici piuttosto grossolani. La teoria materialistica più radicale era quella avanzata da Epicuro (341-270) alla fine del IV sec. a.C. e riproposta da Tito Lucrezio Caro nella prima metà del I sec. a.C. Entrambi questi pensatori spiegavano la visione in termini di copie di dimensione atomica (eídōla o simulacra) che si staccano continuamente dagli oggetti e sono proiettate verso l'esterno in tutte le direzioni. Queste copie, mantenendo durante la proiezione il loro assetto originario, servono come rappresentazioni formali degli oggetti dai quali provengono e, come tali, costituiscono le immagini necessarie alla visione. Nel De rerum natura (IV, 230-238) Lucrezio sostiene che queste immagini, entrando negli occhi, sono sentite visivamente in un modo simile a come sentiamo la forma con le mani: entrambi i tipi di sensazione sono riducibili a interazioni atomiche. In questo modo la vista non sarebbe altro che una specie di tatto.
Meno radicale nelle sue connotazioni materialistiche è la teoria attribuita a Democrito, il quale identificava le entità mediatrici per la vista non nelle copie atomiche, ma nelle impressioni fisiche prodotte da queste copie nell'aria circostante. Alla fine, quando queste impressioni raggiungevano la superficie dell'occhio vi erano impresse sopra dall'émphasis ('riflessione' o 'presentazione'); il risultato era una sorta di impronta rappresentativa dalla quale era tratta l'immagine visiva. Per Democrito, quindi, gli oggetti esterni si facevano percepire visivamente in modo indiretto mediante effetti fisici, piuttosto che direttamente mediante copie materiali. Di conseguenza, nella sua teoria, il mezzo attraverso il quale questi effetti erano trasmessi all'occhio veniva ad assumere un significato decisivo.
Tuttavia, ancor più di Democrito è stato Aristotele a sottolineare l'importanza dell'aria come mezzo necessario per la trasmissione all'occhio dell'informazione visiva. La chiave per capire la teoria di Aristotele sta nella sua concezione di che cosa sono la 'potenza' e l''atto'. L'aria, per esempio (oppure ogni altro mezzo ottico, come l'acqua), è unica nel suo essere potenzialmente trasparente. Per diventare trasparente in atto, però, deve essere illuminata; di conseguenza, la luce è definita per la sua potenzialità di rendere tali mezzi attualmente trasparenti. Gli oggetti, da parte loro, sono potenzialmente visibili in virtù del loro colore, che costituisce il 'sensibile proprio' della vista. L'occhio, infatti, possiede un'unica potenzialità: rendere sensibile il colore (e soltanto il colore) mediante la vista. Quindi, per essere visto, un oggetto deve condurre il suo colore all'occhio e lo fa producendo un'alterazione della forma nel mezzo aria, trasformandolo da essenzialmente trasparente ad accidentalmente colorato. Propagandosi istantaneamente attraverso il mezzo, che deve essere assolutamente continuo, quest'alterazione della forma raggiunge l'occhio, dove è attualizzata la sua potenzialità di essere vista. In termini causali, il mezzo trasparente continuo e l'occhio costituiscono la causa materiale, il colore la causa formale e quella efficiente e il vedere la causa finale della visione.
Sia Aristotele sia gli atomisti proposero una teoria fondamentalmente intromissionista e sottolinearono la causazione materiale, ma qui le somiglianze finiscono. A differenza degli atomisti, che fondamentalmente spiegavano la luce in termini di particelle emesse da sorgenti luminose, Aristotele la concepiva non come una sorgente diretta od oggetto proprio della vista, ma come un catalizzatore di essa, con l'unica funzione di attualizzare la trasparenza: di qui la caratterizzazione della luce come "il colore della trasparenza". Sempre a differenza degli atomisti, Aristotele poneva la causa prossima della visione non in una materia proiettata attraverso lo spazio o in impulsi meccanici che si propagano nell'aria, ma in effetti formali trasmessi attraverso un substrato materiale continuo. Aristotele, quindi, rifiutava di assumere come base per la visione rappresentazioni materiali a favore di quelle qualitative e ciò era collegato, come si vedrà, alla sua posizione sull'astrazione percettiva e su quella intellettiva.
Per quanto riguarda le teorie estromissioniste, le versioni più antiche si basavano sull'idea che l'occhio vedesse diffondendo la propria luce sugli oggetti visibili. Questo sembra valere sicuramente per il pitagorico Alcmeone (attivo intorno al 500 a.C.), che, secondo Aristotele, aveva dedotto che l'occhio contiene fuoco innato a causa del lampo che si vede quando esso è colpito. Empedocle (V sec. a.C.) è andato oltre, paragonando l'occhio a una lanterna il cui fuoco brilla fino agli oggetti circostanti, attraverso membrane protettive trasparenti. La stessa idea, cioè che la visione sia dovuta all'emissione di fuoco o luce intraoculare, in Problemata XXXI sembra essere alla base della spiegazione del perché i miopi socchiudano gli occhi per vedere: secondo quest'ipotesi, infatti, essi concentrano la corrente della visione (ópsis) restringendo l'apertura attraverso cui essa fluisce.
La teoria euclideo-tolemaica dei raggi visivi, che rientri davvero o meno all'interno di questa tradizione pitagorica, mostra evidenti affinità con essa, sebbene a un livello generale e non specifico. L'ipotesi di base della teoria dei raggi visivi è la seguente: l'occhio emette un flusso visivo lungo linee radiali a partire da un punto collocato al suo interno. Queste linee radiali, formando un fascio che diverge in modo costante a mano a mano che procedono verso l'esterno, producono un cono il cui vertice costituisce il centro della (o di) vista e la cui base rappresenta il campo visivo. Tutto ciò che, all'interno di questo campo, è toccato dal flusso visivo è visto; ciò che non è toccato rimane invisibile. Quindi, diversamente dagli atomisti, per i quali l'occhio era un recettore passivo, i sostenitori della teoria dei raggi visivi lo consideravano l'agente primario della vista.
La terza e ultima alternativa teorica, cioè la forma mista tra l'ipotesi intromissionista e quella estromissionista, fu adottata da Platone e dagli stoici. Così come è formulata nel Timeo, infatti, la teoria di Platone sembra incorporare elementi sia della concezione atomistica sia di quella pitagorica. In un passo del Timeo (45b-c) Platone sembra prendere una posizione fondamentalmente estromissionista, spiegando la visione sulla base di un fuoco oculare che fluisce dagli occhi. Mescolandosi con la luce del giorno, questa corrente ignea forma un corpo omogeneo che unisce fisicamente e visivamente sia l'occhio sia l'oggetto: è quindi attraverso questo legame che l'oggetto è percepito visivamente. Più avanti però, quando passa a trattare il problema della percezione del colore, Platone inclina verso l'intromissionismo (Timaeus, 67 d-e): la percezione del colore, spiega, risulta da una collisione tra il flusso di fuoco che emana dall'occhio e una corrente di particelle che emana dagli oggetti colorati. A seconda della dimensione di queste particelle, il fuoco oculare rimane inalterato oppure è dilatato o contratto. Il risultato è la percezione della trasparenza (se non c'è alterazione), della bianchezza (se c'è dilatazione) o della nerezza (se c'è contrazione). Secondo Platone, quindi, il colore è fondamentalmente di origine soggettiva piuttosto che oggettiva, un'affezione psicologica piuttosto che un effetto fisico.
Gli stoici, invece, spiegavano la visione nei termini di una cooperazione tra la luce esterna e il pneuma oculare, che è una sorta di flusso igneo che emana dall'occhio nell'aria circostante. Una volta venuta a contatto con il pneuma oculare, l'aria, se adeguatamente illuminata, si trasforma in un'estensione percipiente dell'occhio, creando un legame simpatetico tra l'occhio e tutti gli oggetti che si trovano all'interno del suo campo visivo. Secondo Galeno questo legame simpatetico è analogo a un bastone da passeggio per mezzo del quale la mano riesce a sentire gli oggetti circostanti. Per gli stoici, quindi, la vista sembrerebbe essere una forma di tatto e il processo visivo nel suo complesso comprenderebbe un'estensione dell'occhio verso l'esterno e un'estensione complementare verso l'interno dell'informazione visiva appropriata.
Nessuna di queste teorie, con l'eccezione forse della teoria atomistica, tratta dunque la luce in maniera indipendente o ne offre una spiegazione fisica coerente. Per lo più, infatti, la luce non è neppure considerata dai teorici antichi come visibile di per sé; essa, invece, assume il ruolo di agente secondario della visione: attualizzando la trasparenza potenziale del mezzo (Aristotele); combinandosi, nella sua forma aerea, con il fuoco oculare per facilitare il contatto visivo con gli oggetti esterni (Platone); pneumatizzando il mezzo aria per prepararlo alla trasformazione percettiva a opera del pneuma psichico emesso attraverso la superficie corneale dell'occhio (stoici e Galeno); infine, illuminando gli oggetti esterni per rendere effettivamente visibili i loro colori (Tolomeo). In nessuno di questi casi la luce emerge come un'entità fisica il cui status funzionale sia sostanzialmente indipendente dalla percezione visiva.
Modelli anatomici e fisiologici
Per il periodo precedente al 300 a.C. non abbiamo testimonianze di un modello anatomico o fisiologico della visione chiaramente formulato, anche se ci furono tentativi di spiegare la natura funzionale dell'occhio sulla base della sua struttura fisica o della composizione elementare. Empedocle, per esempio, credeva che l'occhio contenesse passaggi della misura giusta per accogliere proprio quelle particelle che, entrando, suscitavano la visione e non, per esempio, la sensazione di calore o quella di durezza. Democrito sottolineava la natura acquea dell'occhio, che, secondo la sua ipotesi, lo rendeva particolarmente suscettibile alle impressioni cosiddette 'enfatiche' che servivano da immagini visibili. Aristotele era d'accordo con Democrito nel sostenere che l'umore oculare era fondamentale per la vista, tuttavia non perché tale umore si prestasse alle impressioni enfatiche, ma perché la sua trasparenza permetteva alle forme di colore visibili di passare dentro e attraverso gli occhi.
Mentre Democrito e Aristotele prendevano in considerazione l'acqua, Diogene di Apollonia (attivo intorno al 430 a.C.) pensava all'aria come al fondamento elementare della visione in quanto principio animatore di tutte le forme di vita. Egli supponeva che l'aria, pervadendo il cervello e l'occhio, così come tutti gli altri canali dei sensi, formasse un mezzo continuo attraverso il quale le impressioni sensoriali in generale e quelle visibili in particolare potessero passare all'interno fino alla sede della percezione. Retrospettivamente, questa spiegazione è significativa per due ragioni: in primo luogo, perché l'aria di Diogene sembra preludere al pneuma delle teorie successive; in secondo luogo, perché Diogene, rispondendo forse a suggestioni di Alcmeone, assegnava al cervello un ruolo centrale nella percezione.
Per quanto riguarda l'anatomia del sistema visivo, sembra che Diogene e Aristotele (come forse Alcmeone) fossero stati a conoscenza dell'esistenza dei nervi ottici e del loro collegamento con il cervello e che considerassero questi nervi come passaggi o dotti. Tuttavia non esiste alcuna prova che essi avessero più di una vaghissima idea sul significato funzionale di questi nervi o che avessero ragioni anatomiche per supporre che formassero dotti. Di solito, la vera scoperta dei nervi ottici è attribuita al medico alessandrino Erofilo, che, insieme al suo più giovane collega Erasistrato, isolò il canale ottico come parte di una struttura neurologica complessiva centrata sul cervello e costituita di nervi sensoriali e motori. Inoltre, si dice che Erofilo avesse distinto nell'occhio quattro diverse tuniche (tra cui la retina, la cornea e l'iride) e che, forse, sia stato il primo a osservare il lume, o apertura, nei nervi ottici; di qui deriverebbe la sua convinzione che essi formassero dotti o condotti. Insieme a questo sistema neurologico, Erofilo ed Erasistrato articolarono un modello della sensazione basato sull'ipotesi che, in quanto supremo principio guida, il cervello agisce ed è agito attraverso il pneuma, il quale è diffuso in tutti i canali nervosi che si dipartono dal cervello stesso. Il percorso visivo che inizia dall'occhio e che si dirama attraverso i nervi ottici cavi è quindi riempito con il pneuma che si origina nel cervello. Quest'ultimo non soltanto dirige fisicamente il sistema ottico attraverso il pneuma come mezzo, ma valuta anche l'informazione visiva che gli è ritrasmessa sempre attraverso lo stesso pneuma. È il cervello, in definitiva, il responsabile dell'inizio e della conclusione del processo della percezione visiva.
Questa è certamente l'opinione di Galeno, che, sebbene sia stato sicuramente influenzato dagli stoici, tuttavia seguiva Erofilo (e Platone) nel collocare la facoltà guida (hēgemonikón) nel cervello invece che nel cuore, dove la collocavano invece gli stoici (e Aristotele). Galeno, inoltre, aggiunse alcuni dettagli al modello anatomico e fisiologico di Erofilo ed Erasistrato: per esempio, fornì una circostanziata descrizione della produzione del 'pneuma psichico' (pneũma psychikón) nel cervello secondo i vari gradi di elaborazione nel cuore e nel sistema arterioso. Questo sistema, alla fine, alimentava i ventricoli del cervello attraverso la rete mirabile. Il pneuma, scorrendo attraverso il canale ottico, serviva inoltre da mezzo per la percezione, proprio come sostenevano Erofilo e gli stoici.
Come gli stoici, inoltre, Galeno credeva che, quando era colpita dal pneuma oculare che defluiva attraverso la superficie della cornea, l'aria illuminata che circonda l'occhio fosse trasformata in un'estensione percipiente dello stesso. Tuttavia, egli si differenziava dagli stoici per due aspetti decisivi: innanzitutto, rifiutava l'analogia con il bastone da passeggio e l'implicazione che la vista potesse essere ridotta a una forma di contatto fisico. Al contrario, egli sottolineava l'importanza primaria del colore nel processo visivo, facendone l'oggetto proprio della vista e spiegando così la visione in termini di trasmissione del colore all'occhio attraverso il mezzo pneumatizzato. Galeno, inoltre, localizzava la sede della sensibilità visiva nel cristallino, che doveva questa sensibilità al carico di pneuma visivo proveniente dal cervello. Perciò lo stadio 'soggettivo' della percezione visiva cominciava sulla superficie anteriore del cristallino, dove gli effetti di colore passati attraverso l'aria pneumatizzata producevano il loro primo impatto sensibile.
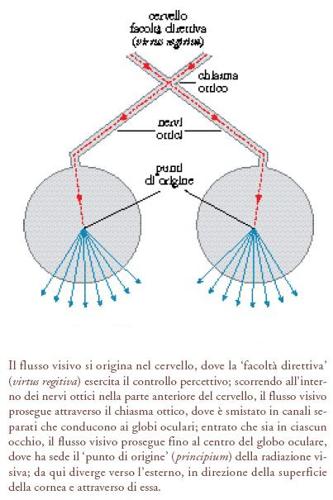
Nel formulare le sue tesi di anatomia e fisiologia dell'occhio, Galeno attinse evidentemente al modello 'alessandrino' di Erofilo ed Erasistrato; probabilmente anche Tolomeo nell'Ottica si era ispirato a questo stesso modello nel concepire la sua teoria della visione. Egli situava il suo principio guida (virtus regitiva o 'facoltà direttiva') nel cervello, per mezzo del quale erano regolate tutte le funzioni dei sensi mediante un 'principio nervoso' (principium nervosum) che si estendeva ininterrottamente fino agli occhi attraverso i due nervi ottici. È anche probabile che Tolomeo conoscesse il chiasma ottico e lo concepisse funzionalmente come il luogo in cui erano fuse le due immagini generate dagli occhi. Egli riteneva che la sede della sensibilità visiva fosse sulla superficie della cornea, dove l'effetto di colore trasmesso all'occhio produceva un'impressione sensibile. Tolomeo, quindi, sembra aver fatto proprio un modello della visione che nelle sue linee generali non differiva da quello di Galeno; in questo caso si può concludere con un certo grado di sicurezza che il flusso visivo ipotizzato da Tolomeo non fosse altro che un pneuma di tipo geometrico (fig. 2).
La psicologia della percezione visiva
Un elemento comune a tutte le teorie della visione proposte nell'Antichità consisteva nell'idea che ciò che si vedeva non fosse l'oggetto vero e proprio, ma 'qualcosa' concernente l'oggetto. In altre parole, si pensava che la vista fosse mediata da qualcosa che rappresentava l'oggetto visibile, sia che fosse un simulacro, un'impressione fisica sulla cornea, una dilatazione o una contrazione del fuoco oculare, o un'impressione di colore trasmessa all'occhio attraverso il mezzo trasparente. Ma allora ci si poteva chiedere come fosse possibile 'vedere' cose che non erano nell'ente mediatore come la dimensione, la distanza o il movimento; come fosse possibile, per esempio, riconoscere che un certo oggetto era alto un po' meno di due metri se l'impressione di colore che lo rappresentava era necessariamente abbastanza piccola da stare sulla superficie della cornea; come si potesse riconoscere che l'oggetto in questione era un uomo, se l'impressione di colore che lo rappresentava chiaramente non poteva contenere la nozione di uomo; oppure perché, di fatto, si vedeva l'oggetto rappresentato invece dell'ente mediatore che lo rappresentava. Evidentemente, la visione non comportava soltanto la percezione fisica di dati sensoriali, ma anche giudizi inferenziali che si basavano su quei dati e andavano al di là di essi; perciò l'iniziale impressione dei sensi doveva avere implicazioni ulteriori e la facoltà sensoriale doveva essere capace di coglierle.
Sebbene sia probabile che vari pensatori avessero già riconosciuto questo fatto, Aristotele però è il primo a prenderlo pienamente in considerazione nella teoria della percezione sensoriale sviluppata nel Libro II e nel Libro III del De anima. La chiave per capire questa teoria sta nella distinzione in essa operata tra "sensibili (aisthētá) speciali", "sensibili comuni" e "sensibili accidentali". Per ogni senso, afferma Aristotele, c'è un sensibile speciale che è adatto unicamente a quello e a nessun altro: il sapore è adatto al gusto, ma non alla vista, mentre il colore è adatto alla vista, ma non al tatto. Tuttavia vi sono certi sensibili che si possono apprendere con più di un senso, come la forma, per esempio, che può essere vista e sentita al tatto, così come la quiete e il moto; questi sensibili, perciò, sono definiti 'comuni'. Infine, vi sono sensibili che vanno anche al di là di questi, come ‒ per fare l'esempio dello stesso Aristotele ‒ il fatto che l'immagine bianca di fronte a noi sia il figlio di Diare. In effetti queste caratteristiche accidentali non sono per niente sensibili, ma sono il risultato di giudizio percettivo e di inferenza. In questa triplice differenziazione dei sensibili è implicito un modello di percezione sensoriale articolato in tre distinti livelli di conoscenza. In termini di visione, per esempio, al livello più basso si percepiscono gli effetti di colore trasmessi agli occhi attraverso i mezzi continui trasparenti. Oggettivamente, le impressioni che ne risultano consistono soltanto dei colori e dei loro contrasti; tuttavia, come i dipinti, tali impressioni di colore agiscono da rappresentazioni, trasmettendo attributi spaziali - come dimensione, forma, distanza e così via - che sono impliciti ma non realmente presenti in esse. Questi attributi sono inferiti dal cosiddetto 'senso comune' (aísthēsis koinḗ), una facoltà dell'anima che agisce come una sorta di camera di compensazione per tutti i sensibili che si trovano a una certa distanza percettiva dai sensibili speciali. Dunque è attraverso il senso comune che le disparate impressioni sensibili di 'rosso', 'rotondo', 'liscio', 'dolce', 'piccolo' e 'duro' convogliate attraverso i cinque sensi esterni sono riunite in un'impressione percettibile unitaria di 'mela'.
Che Aristotele distinguesse tra mera sensazione (che ha come oggetto i sensibilia) e percezione (che ha come oggetto i perceptibilia) è evidente, anche se questa differenza non si riflette nel suo vocabolario. Entrambi i processi, infatti, sono designati dal termine complessivo aísthēsis e i loro rispettivi oggetti dal termine aisthētón. Analogamente, nonostante il vocabolario, Aristotele distingueva tra 'percezione' e ciò che può essere chiamato 'appercezione': il livello al quale si apprendono i sensibili accidentali (cioè gli intelligibilia), che sono inferiti attraverso la ragione e il riconoscimento. Nel complesso, la teoria della percezione sensoriale elaborata da Aristotele può essere capita meglio nel contesto della sua teoria dell'astrazione: i sensibilia (sensibili speciali) si trovano al livello di astrazione più basso; i perceptibilia (sensibili comuni) a un livello più elevato e gli intelligibilia (sensibili accidentali) al livello di astrazione più alto.
Sostanzialmente è questo schema percettivo che, con opportuni aggiustamenti per adeguarlo al modello estromissionistico di radiazione, fu adottato da Tolomeo nella sua teoria della visione contenuta nell'Ottica. Si prenda la sua gradazione degli oggetti visibili (res visibiles). Secondo Tolomeo, tali oggetti esistono a tre livelli: quelli che sono "visibili intrinsecamente" (quae vere videntur), quelli che sono "visibili primariamente" (quae primo videntur) e quelli che sono "visibili secondariamente" (quae sequenter videntur). Al livello della visibilità intrinseca sta la "compattezza luminosa" (lucida spissa), che non è visibile di per sé, ma nondimeno è un prerequisito per la visione, in quanto rende gli oggetti effettivamente sensibili al flusso visivo incidente. I colori, d'altro canto, sono visibili primariamente, poiché costituiscono l'oggetto proprio (e perciò il solo) della visione. Dunque, anche per Tolomeo, così come per Aristotele, la luce funziona da catalizzatore piuttosto che come un vero oggetto della visione e il colore funziona come dato sensoriale primario della visione.
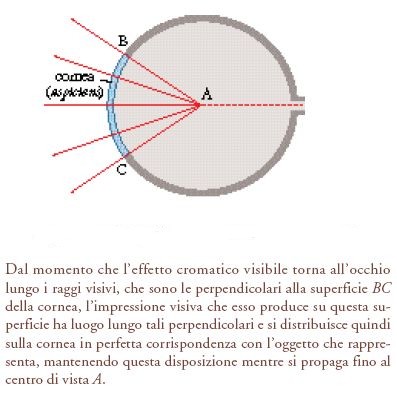
A un primo approccio, Aristotele può sembrare una strana fonte d'ispirazione teorica per Tolomeo. Per Aristotele, dopo tutto, l'occhio non riveste alcun ruolo nel trasformare l'oggetto da potenzialmente ad attualmente visibile, mentre per Tolomeo esso ha un ruolo centrale. Tuttavia, nonostante questa differenza fondamentale sul modo in cui si stabilisce il contatto fisico tra l'occhio e l'oggetto, entrambi concordano sul fatto che l'effetto di colore che ne risulta, essendo qualitativo, richiede un sostrato materiale per essere trasmesso fino all'occhio. Secondo Tolomeo, questo sostrato è costituito dal flusso visivo, che subisce la 'passione' (passio) della 'colorazione' (coloratio) colpendo l'oggetto potenzialmente visibile (cioè luminoso e compatto); questa passione è poi ritrasmessa indietro attraverso il flusso visivo fino alla superficie della cornea (il termine di Tolomeo per la cornea è aspiciens o 'vedente'), dove produce un'impressione di colore sensibile; è dunque sulla superficie della cornea, che ha inizio la sensazione visiva (fig. 3).
Una volta che l'impressione di colore è percepita sensibilmente sulla superficie della cornea, essa passa all'interno attraverso il flusso che riempie il complesso ottico che conduce alla parte anteriore del cervello, che è la sede della facoltà direttiva. Questa, esercitando la sua capacità di discriminazione (virtus discernitiva), desume dalle impressioni di colore che le si presentano i visibili secondari, i quali consistono di attributi spaziali come dimensione, forma e distanza. Sotto questo aspetto, quindi, la facoltà direttiva opera praticamente nello stesso modo del senso comune di Aristotele, astraendo informazioni che sono implicite, ma non realmente presenti, nelle impressioni sensibili. I visibili secondari di Tolomeo sono sostanzialmente la stessa cosa dei sensibili comuni di Aristotele e forniscono una rappresentazione percettiva completa dell'oggetto in tutti i suoi dettagli fisici rilevanti.
Sebbene fondasse la sua teoria della percezione spaziale sulla geometria dei raggi, nondimeno Tolomeo era ben consapevole dell'impossibilità di spiegare in modo esauriente la percezione di certe caratteristiche spaziali, come distanza e dimensione, solamente sulla base della geometria dei raggi. Ci sono in gioco anche fattori psicologici: la brillantezza relativa dei colori, per esempio, può condurre alla percezione (o meglio all'errata percezione) che, tra oggetti della stessa dimensione che si trovino a uguale distanza, i più debolmente colorati siano più lontani ‒ di qui l'uso della prospettiva dei colori tra i pittori murali per dare l'effetto di profondità spaziale nei loro paesaggi. Così anche oggetti lontani, quali il Sole o la Luna, sono percepiti molto più grandi quando sono all'orizzonte che quando sono allo zenit, sebbene in entrambe le posizioni essi abbiano esattamente la stessa dimensione angolare. Quindi, come l'errata percezione della dimensione relativa o della profondità spaziale dovuta alla brillantezza variabile dei colori, questo errore di percezione (generalmente conosciuto come l''illusione della Luna') è di origine interamente psicologica, non fisica o sensibile.
Quale notevole rilievo nella sua teoria della percezione visiva Tolomeo attribuisse alla psicologia diventa chiaro se si esamina la sua tipologia delle illusioni ottiche, alle quali dedica una considerevole parte del Libro II dell'Ottica. Secondo Tolomeo esistono tre tipi di illusioni ottiche: il primo e più elementare riguarda le anomalie che si possono verificare nelle circostanze fisiche in cui ha luogo la visione e deriva generalmente dal mancato raggiungimento delle condizioni-soglia. Per fare un esempio, nella miopia non si vedono bene gli oggetti lontani poiché il flusso visivo che li raggiunge è troppo scarso. Su un disco che ruota, i singoli colori sono visti mescolati e non separati poiché si muovono a velocità troppo elevata per poter essere distinti. Un oggetto opaco posto vicino a uno estremamente brillante appare ancora più opaco di quanto sia, poiché è messo in ombra dal suo più brillante vicino. Percezioni errate di questo tipo hanno un'origine 'oggettiva' più che 'soggettiva'; poiché derivano da anomalie nelle condizioni fisiche in cui ha luogo la visione.
Il secondo tipo di illusioni, invece, si verifica a livello della sensazione ed è perciò d'origine autenticamente soggettiva. Queste illusioni risultano da certe 'passioni' (a parte la colorazione) che fanno sì che il flusso visivo agisca in modo anomalo; una rottura, o rimbalzo completo, del flusso visivo su una superficie riflettente costituisce una di tali 'passioni', che, di solito, ha come esito il fatto che l'oggetto è visto dietro la superficie e non dove si trova davvero. Anche un'incurvatura, o rimbalzo incompleto, del flusso su una superficie rifrangente dà luogo a un'errata percezione della posizione, con l'oggetto che sembra stare più vicino o più lontano di quanto realmente si trovi. Inoltre, sia l'incurvatura sia la rottura del flusso visivo possono distorcere la forma o la dimensione dell'oggetto percepito. La cosiddetta 'illusione oculogira' è un altro esempio di come effetti fisici subiti dal flusso visivo possono causare false percezioni; essa si verifica quando per un po' di tempo giriamo velocemente su noi stessi e poi ci fermiamo: le cose che ci circondano sembrano ruotare intorno a noi.
La causa principale di questa percezione errata è, spiega Tolomeo, una sorta di vortice inerziale che continua a far scorrere rapidamente il flusso visivo sopra gli oggetti circostanti; consapevoli della nostra immobilità, siamo così portati a inferire che il movimento percepito sia negli oggetti che ci circondano, non in noi. Il terzo tipo di illusione si verifica al livello della percezione e della ragione: esse derivano da un errato giudizio psicologico piuttosto che da circostanze fisiche o da 'passioni' subite dal flusso visivo. A questo riguardo un esempio significativo è dato dalla percezione della profondità dovuta all'ombreggiatura, che risulta da particolari contrasti cromatici, usati dai pittori illusionisti per trarci in inganno nella percezione della profondità nelle scene dipinte su muri piani. Lo stesso vale per la prospettiva cromatica, usata dai pittori nei paesaggi per dare l'illusione della distanza: più lontano si vuol far apparire un oggetto, più opaco e indistinto è il colore con il quale esso è reso. Di origine psicologica è anche l'illusione che ha luogo quando, stando fermi nell'acqua che scorre velocemente, abbiamo l'impressione di essere noi a muoverci e non l'acqua; o quando, posti su una barca, siamo lentamente trasportati dalla corrente del fiume e a noi talora sembra che sia la linea di costa a muoversi e non viceversa. In questa descrizione delle illusioni ottiche sono degni di nota quattro aspetti. In primo luogo, il fatto stesso che esista: infatti, non si conoscono precedenti di nessun tipo per un esame così completo delle illusioni ottiche e delle loro presunte cause. Secondariamente, non soltanto l'esame è completo, ma è anche sistematico. In terzo luogo, questa tipologia tripartita rivela un modello di percezione visiva fondamentalmente di tipo aristotelico; secondo questo modello, infatti, la visione si svolge in fasi distinte, ma interdipendenti, cominciando con l'impressione fisica, passando attraverso la sensazione e la percezione e culminando nella conoscenza intellettuale. Infine, la fusione di questo modello della percezione visiva a più fasi con il modello alessandrino di psicologia della visione dà alla teoria di Tolomeo una coerenza e una completezza alla quale nessuno dei suoi predecessori si era avvicinato.
L'ottica matematica e la teoria dei raggi visivi
L'ottica propriamente detta: l'analisi della visione diretta
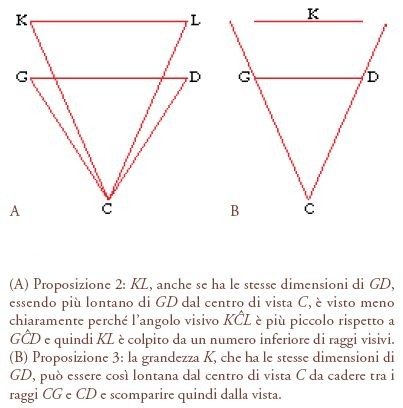
Che il concetto di raggio sia precedente all'opera di Euclide è evidente dall'uso che, nel Libro III dei Meteorologica, Aristotele fa dello studio dei raggi per spiegare la formazione dell'arcobaleno. A tutti gli effetti, però, le origini della teoria dei raggi greca risalgono all'Ottica di Euclide, dal momento che questa breve opera rappresenta il primo approccio sistematico all'ottica geometrica. Euclide pone le basi teoriche del proprio pensiero nei primi tre postulati dell'Ottica, dove descrive la generazione del cono visivo: "Supponiamo che linee rette divergano dagli occhi verso l'esterno […] che questi raggi visivi formino un cono il cui vertice è collocato nell'occhio e la cui base si forma sui confini degli oggetti visibili; [e] che gli oggetti con i quali il flusso visivo entra in contatto siano visti". Essendo assolutamente discreti, questi raggi visivi divergono sotto forma di fasci dal vertice del cono visivo verso l'esterno, e, così facendo, gli intervalli esistenti fra di essi si ampliano. È sulla base di questi intervalli interradiali che Euclide spiega la variazione dell'acutezza visiva con la distanza; nella seconda proposizione dell'Ottica, infatti, egli afferma che lo stesso oggetto è visto tanto meno chiaramente, quanto più lontano si trovi dal centro della vista, in quanto sottende un angolo visivo più piccolo ed è quindi toccato da un numero minore di raggi visivi. Nella proposizione successiva, poi, egli dimostra che per ogni oggetto esiste una distanza alla quale esso scomparirà dalla vista, in quanto cade negli intervalli interradiali ed è quindi invisibile (fig. 4).
Il problema principale di questa concezione dei raggi visivi è che, se la visione dovesse aver luogo mediante raggi discreti, allora ogni cosa dovrebbe apparire discontinua, in forma puntiforme, piuttosto che continua. Tolomeo si rende conto di questo problema e lo risolve affermando che, in realtà, il flusso visivo non emana dall'occhio sotto forma di fasci radiali, ma come un vero e proprio continuo. Tuttavia, anche se il cono visivo che ne risulta è continuo, per ragioni di studio può essere trattato come se fosse composto di raggi visivi discreti, che perciò devono essere considerati entità virtuali piuttosto che reali. Alla luce di queste considerazioni egli spiega le variazioni nell'acutezza visiva non in base agli intervalli interradiali, ma all'intensità della radiazione visiva misurata lungo il raggio assiale immaginario che si estende dal vertice del cono visivo, che si trova proprio al centro dell'occhio. Più lontano è posto l'oggetto lungo l'asse visivo, meno intensa è la radiazione visiva che lo colpisce e, quindi, meno chiaramente è visto. Analogamente, più grande è la distanza laterale dell'oggetto dall'asse visivo, più obliquamente è colpito dai raggi incidenti. Inoltre, via via che l'impatto diventa più obliquo esso sarà progressivamente meno intenso, e, quindi, l'oggetto sarà visto meno chiaramente. Dunque, qualunque sia la distanza lineare tra l'occhio e l'oggetto, lungo l'asse visivo la visione risulterà costantemente più chiara.
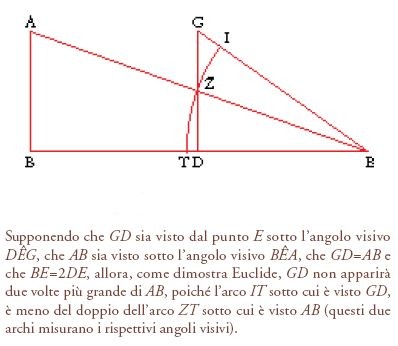
La funzione principale del cono visivo come strumento analitico è di rendere conto della percezione spaziale. Sia Euclide che Tolomeo, per esempio, forniscono ai raggi una direzione privilegiata cosicché le cose colpite dai raggi più a sinistra appaiono più a sinistra delle cose colpite più a destra. Lo stesso vale per la percezione dell'alto e del basso. È la direzione privilegiata a spiegare perché linee parallele sembrano convergere alla distanza. Più le linee si allontanano dal centro di vista, più a sinistra sono i raggi che colpiscono la linea di destra e più a destra sono i raggi che colpiscono la linea di sinistra. Così pure, quando un piano è visto da un'altura, le sue zone più lontane appaiono più alte di quelle più vicine, poiché sono viste per mezzo di raggi più alti. La nostra abilità nel percepire la direzione dei raggi è quindi un fattore decisivo nella percezione dello spazio, in quanto ci permette di mappare il campo visivo in orizzontale e in verticale. In questo processo un altro fattore decisivo è l'angolo al vertice del cono visivo, dal momento che quest'angolo è fondamentale nella nostra percezione della dimensione. Come spiega Euclide nella prop. 5 dell'Ottica, più largo è il campo visivo sotteso da un dato oggetto, più grande appare quest'oggetto, sebbene, come mostra nella prop. 8, il cambio di dimensione apparente non sia proporzionale alla distanza, in quanto lo stesso oggetto visto a una distanza doppia non appare grande la metà (fig. 5). Mentre Euclide fa dipendere la valutazione della dimensione soltanto dall'angolo visivo, Tolomeo si rende conto del fatto che nel processo è implicato molto più di questo; dopo tutto, noi non percepiamo un albero vicino come più grande di una montagna lontana, anche se l'angolo visivo sotteso dal primo può essere considerevolmente maggiore di quello sotteso dalla seconda.
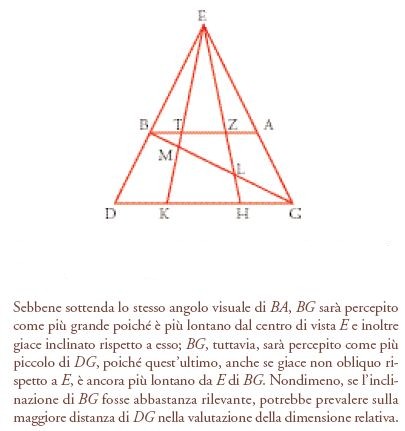
Nella percezione della dimensione, dunque, Tolomeo adduce due fattori supplementari: in primo luogo la distanza. Entro limiti ragionevoli, afferma nel Libro II dell'Ottica, abbiamo una capacità innata di giudicare la distanza grazie alla lunghezza dei raggi. Di conseguenza, due oggetti possono sottendere angoli visivi uguali, ma se uno di essi è visto con raggi più lunghi e, per questa ragione, si ritiene che si trovi più lontano dal punto di vista, sarà percepito come più grande dell'altro. Tuttavia, la distanza e l'angolo visivo non sono gli unici fattori che determinano la percezione della dimensione; anche l'orientamento e l'inclinazione giocano un ruolo. Di conseguenza, di due oggetti che sottendono angoli visivi uguali e che giacciono esattamente alla stessa distanza dall'occhio lungo l'asse visivo, quello che è più obliquo rispetto al punto di vista sarà percepito come più grande (fig. 6). Nondimeno, la nostra valutazione definitiva della dimensione non dipende soltanto dalla geometria, ma anche dalla psicologia. In certe circostanze, perciò, nella percezione della dimensione relativa di un certo oggetto l'inclinazione può prevalere sulla distanza o sull'angolo; mentre, in altre circostanze, la distanza può prevalere sull'inclinazione o sull'angolo. Inoltre, come già si è detto, la brillantezza relativa di un oggetto può influenzare la percezione della sua dimensione.
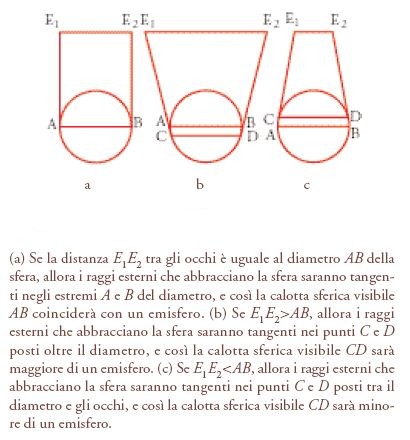
Euclide analizza i raggi sulla base di un singolo cono visivo e, quindi, di un singolo centro della visione. Egli, cioè, ignora quasi completamente il problema della visione binoculare, anche se lo affronta indirettamente nelle proposizioni 25-27 dell'Ottica, nelle quali egli mette in relazione la dimensione della calotta sferica, vista con entrambi gli occhi, con la distanza tra gli occhi e il diametro della sfera: se sono uguali, si vedrà un emisfero; se la prima è maggiore del secondo, si vedrà più di un emisfero; infine, se la prima è minore del secondo si vedrà meno di un emisfero (fig. 7). Tuttavia, concentrandosi sul problema della percezione della dimensione, Euclide rimane ai margini della questione ben più fondamentale di come, in circostanze normali, due occhi producono una e non due immagini. Resta il problema di esaminare le condizioni necessarie e sufficienti per una corretta visione binoculare.
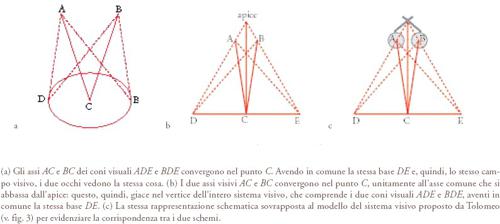
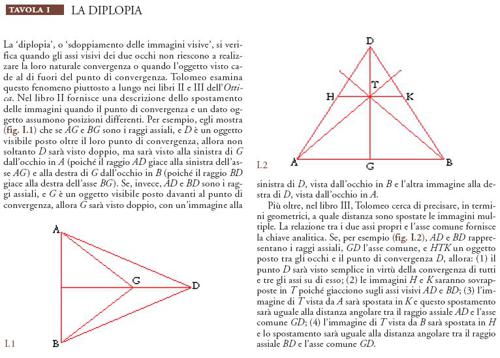
A questo proposito l'analisi di Tolomeo (e forse è la parte più innovativa della sua teoria) suppone che gli occhi lavorino naturalmente di concerto in modo tale da assicurare che le immagini da essi ricavate individualmente siano perfettamente fuse prima di raggiungere la facoltà percettiva. Questa fusione è ottenuta facendo intersecare in un solo punto dell'oggetto visibile gli assi di entrambi i coni visivi. In questo modo i due coni avranno in comune la stessa base e, quindi, lo stesso campo visivo, cosicché vedranno sostanzialmente la stessa cosa (fig. 8a). Gli occhi, tuttavia, non controllano il proprio puntamento; questo ruolo è svolto dalla facoltà direttiva, che agisce per mezzo dell''apice' (principium), dove si uniscono i due nervi ottici (cioè nel chiasma ottico). Formando il vertice dell'intero sistema visivo, l'apice è il punto dove ha origine il cosiddetto 'asse comune', il quale, quindi, fornisce la linea di riferimento fondamentale per l'intero sistema visivo, definendo il punto di intersezione sull'oggetto visibile sul quale i due assi propri del cono visivo devono continuamente convergere, inclinandosi opportunamente l'uno sull'altro (fig. 8b, c).
La trattazione di Tolomeo della visione binoculare ‒ chiave di volta dei suoi studi di ottica propriamente detta ‒ rappresenta una conquista notevole. Essa, tuttavia, non è priva di problemi; per esempio, nel supporre che il campo visivo sia planare, e quindi assumendo che i due coni visivi possano avere in comune la stessa base, Tolomeo non considera il fatto che con due occhi vediamo di più che con uno, un fatto che Galeno invece riconosce occupandosi della visione binoculare nel Libro X del De usu partium. Tolomeo trascura anche il fatto che la visione binoculare permette di vedere a tre dimensioni. A posteriori, naturalmente, l'origine del problema è chiara: l'analisi che Tolomeo fa della visione binoculare è sbilanciata sul versante matematico a scapito di quello psicologico; eppure, nonostante tutti i suoi difetti, essa rappresenta un passo significativo verso una teoria della visione veramente completa.
Catottrica: l'analisi della visione riflessa
Tolomeo include dunque la rottura dei raggi visivi su una superficie riflettente tra quelle 'passioni' subite dal flusso visivo che producono percezioni errate o illusioni. Nel caso della riflessione (come pure della rifrazione), simili errori di percezione derivano dal fatto che, anche se il vero contatto visivo tra il flusso e l'oggetto si ha lungo il raggio riflesso, l'oggetto è percepito sul prolungamento del raggio incidente, come se la rottura non fosse mai avvenuta. Nella riflessione, quindi, siamo sempre ingannati, poiché ciò che noi percepiamo (cioè l'immagine) è un'entità puramente psicologica, un prodotto della nostra immaginazione visiva. Stando così le cose, la funzione principale della catottrica è di razionalizzare la disparità tra ciò che si percepisce nello specchio e ciò che è visto in realtà. In definitiva, questa razionalizzazione si fonda sull'uguaglianza tra l'angolo di incidenza (i) e l'angolo di riflessione (r). L'enunciazione di questa uguaglianza (i=r) costituisce la cosiddetta 'legge degli angoli uguali'.
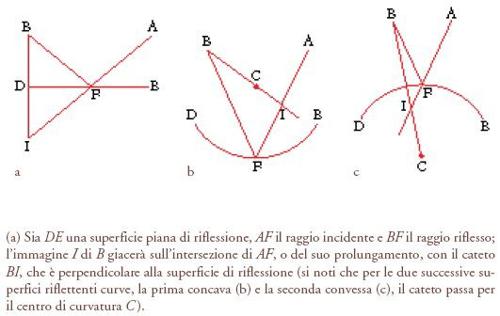
Tale legge è fondamentale per poter determinare la localizzazione dell'immagine nella riflessione; questa, però, dipende anche da altri principî: uno di questi, già menzionato, è che l'immagine appare sul prolungamento della linea d'incidenza; un altro è che l'immagine giace sul cateto di riflessione, che è la perpendicolare condotta dall'oggetto visibile alla superficie riflettente; l'ultimo principio consiste nel fatto che tutte le linee e i punti significativi ‒ cioè il raggio incidente e quello riflesso, il prolungamento del raggio incidente, il cateto, il centro di vista, l'oggetto (preso come punto), il punto di riflessione e l'immagine del punto-oggetto ‒ devono giacere sullo stesso piano. Allora, qualunque sia la forma della superficie riflettente, l'immagine giacerà sull'intersezione tra il raggio incidente, o il suo prolungamento, e il cateto (fig. 9).
Euclide, Erone e Tolomeo erano a conoscenza di questa regola di base per determinare la localizzazione dell'immagine, e tutti e tre l'applicarono in vari modi all'analisi della riflessione. Non sorprende che l'uso che Euclide fece di questa regola sia stato assai meno articolato e sistematico di quello di Tolomeo, mentre Erone se ne servì essenzialmente per spiegare in che modo gli specchi possono essere manovrati per creare effetti ottici sbalorditivi.
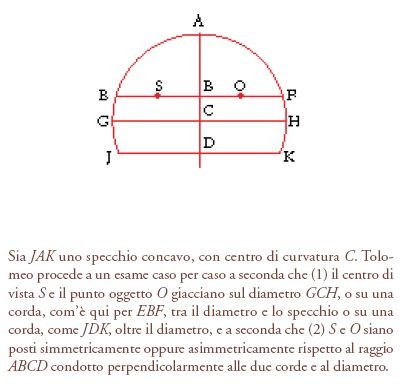
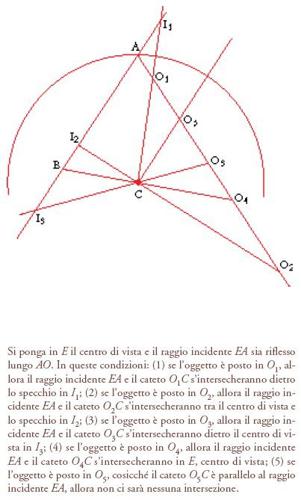
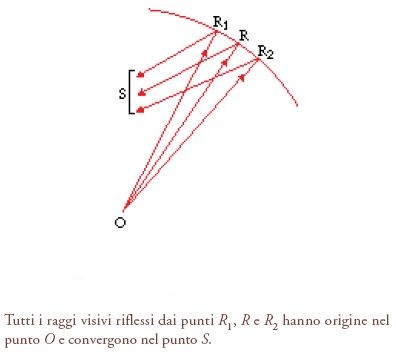
L'analisi che Euclide e Tolomeo hanno dedicato alla formazione e alla distorsione dell'immagine a seconda della forma della superficie riflettente, parte dalla questione delle immagini multiple, cioè se sia possibile vedere in uno specchio più di un'immagine dello stesso oggetto. La risposta è che, mentre da un dato centro della vista negli specchi piani e convessi si può vedere una sola immagine, invece negli specchi concavi a volte se ne può vedere più di una e quindi è possibile stabilire una netta distinzione tra gli specchi concavi, da un lato, e quelli piani e convessi, dall'altro. Questa distinzione si può estendere alla localizzazione delle immagini rispetto alla superficie riflettente: negli specchi concavi le immagini appaiono ora dietro ora davanti a essa, mentre negli specchi piani e convessi appaiono sempre dietro la superficie riflettente. Inoltre, nel caso degli specchi concavi e piani, le immagini sono sempre rovesciate, con la destra al posto della sinistra, ma non capovolte, mentre negli specchi concavi a volte sono capovolte, altre volte non lo sono. Naturalmente vi sono differenze fondamentali tra gli specchi piani e quelli convessi; la forma apparente degli oggetti, per esempio, negli specchi convessi è chiaramente distorta, ma non lo è in quelli piani. Analogamente, negli specchi convessi è alterata la dimensione apparente degli oggetti, che sembrano più piccoli del dovuto; negli specchi piani, invece, gli oggetti mantengono la loro dimensione. Negli specchi convessi anche la distanza apparente degli oggetti è modificata, ma ciò non avviene in quelli piani. Di tutte queste distorsioni Euclide e Tolomeo danno conto in un modo o nell'altro, anche se, come ci si poteva aspettare, la trattazione di Tolomeo è più sistematica di quella di Euclide. Passando all'esame degli specchi concavi, il divario nel grado di elaborazione tra Tolomeo ed Euclide si amplia notevolmente, dal momento che l'approccio di Tolomeo non soltanto è più sistematico, ma anche più comprensivo. Per esempio, a differenza di Euclide, che lo sfiora appena, Tolomeo dedica grande attenzione al problema delle riflessioni multiple negli specchi concavi, mostrando come il numero delle riflessioni (e quindi delle immagini) possibili varia con il variare della collocazione relativa dell'occhio e dell'oggetto rispetto alla superficie riflettente (fig. 10). Anche per quanto riguarda la formazione dell'immagine Tolomeo ha un approccio più sistematico e comprensivo di quello di Euclide. Innanzitutto, egli individua negli specchi concavi cinque casi generali di formazione delle immagini a seconda di dove si intersecano la linea di incidenza e il cateto: come mostra la fig. 11, le due linee possono intersecarsi dietro lo specchio (caso 1), tra l'occhio e la superficie dello specchio (caso 2), dietro l'occhio (caso 3), nel centro della vista (caso 4), o possono non intersecarsi affatto (caso 5). Nei casi 1 e 2 si vede un'immagine nitida; ma cosa avviene negli altri tre casi? La conclusione logica sarebbe che, in queste condizioni, non si veda alcuna immagine. In tutti e cinque i casi, però, il flusso visivo è riflesso verso l'oggetto e quindi vi è contatto visivo; questo significa che, in ogni caso, qualcosa deve essere visto. Così, quando l'intersezione è indeterminata (caso 5) o ha luogo nel centro della vista (caso 4), la facoltà visiva, guidata presumibilmente dalla facoltà direttiva, traspone l'immagine sulla superficie dello specchio. Fondendosi con questa superficie e assumendone quindi il colore, l'immagine diventa indistinguibile da essa e si vede un'immagine fantasma. Quando, invece, l'intersezione ha luogo dietro l'occhio (caso 3), la facoltà visiva traspone l'immagine in un luogo tra l'occhio e lo specchio, dove essa appare vaga e indefinita; ciò che vediamo è quindi determinato psicologicamente piuttosto che matematicamente. Il fatto che, per spiegare questi tre casi, Tolomeo faccia ricorso a fattori psicologici è istruttivo per almeno due motivi. Innanzitutto, egli mette in evidenza la sua idea che tutte le immagini, 'reali' o 'virtuali' secondo gli standard moderni, sono di origine interamente soggettiva e, perciò, non esistono al di fuori di un agente che le percepisce (quest'idea fu sostenuta praticamente da tutti i teorici dell'ottica dopo Tolomeo fino al XVII sec.); in secondo luogo, testimonia la netta priorità dell'aspetto empirico e della coerenza teorica rispetto a quella matematica nella trattazione della percezione visiva.
Diottrica: l'analisi della visione rifratta
Esistono testimonianze, anche se scarse, che indicano come la rifrazione fosse stata oggetto di studio almeno fin dal III sec. a.C. Il postulato VI della Catottrica di Euclide, per esempio, afferma che se un corpo qualsiasi è messo sul fondo di un vaso vuoto, in modo tale da non poter essere visto al di sopra del bordo di questo, esso finisce per apparire al di sopra del bordo, se nel vaso è versata dell'acqua. Apuleio di Madaura (125 ca.-180 ca.) attribuisce ad Archimede (287-212) un trattato sugli specchi in cui, secondo Teone di Alessandria (attivo nel 370 d.C. ca.) e Olimpiodoro (400 d.C. ca.), si sarebbe occupato della rifrazione. Comunque stiano le cose, non vi sono però riscontri testuali che suffraghino tale testimonianza e non vi è nulla, nella testimonianza stessa, che suggerisca un qualche significativo sviluppo nella conoscenza della rifrazione prima che Tolomeo ne intraprendesse uno studio completo nel Libro V dell'Ottica.
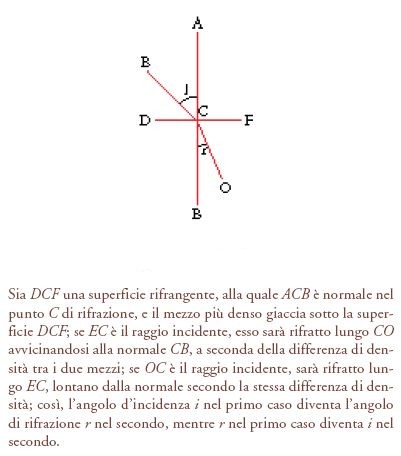
Tolomeo procede in base all'assunto che la rifrazione sia un caso speciale di riflessione. A livello fisico, per esempio, i due tipi di frazionamento (fractio) dei raggi possono essere compresi per analogia con il movimento di un proiettile: la riflessione comporta il perfetto rimbalzo contro una superficie rigida, la rifrazione un rimbalzo imperfetto (passaggio ostacolato) sulla superficie di un mezzo denso ma permeabile, la cui permeabilità lo rende trasparente. Il flusso visivo, colpendo tale superficie e passando nel mezzo, è deviato in direzione della normale a seconda della densità del mezzo. Maggiore è la densità, più forte è la deviazione, sinché, alla fine, la densità diventa sufficiente a rendere la superficie impermeabile. A questo punto la deviazione da rifrazione si trasforma in un rimbalzo di riflessione. Nel passare, invece, da un mezzo più denso a uno più rado, il flusso visivo è deviato lontano dalla normale a seconda della differenza della densità tra i due mezzi; così gli angoli di incidenza e di rifrazione, i e r, sono reciproci e interscambiabili a seconda che si consideri il raggio in entrata o in uscita dal mezzo più denso (fig. 12). Collegate al livello della dinamica, riflessione e rifrazione lo sono anche in altri modi: in entrambi i casi esiste una fondamentale disparità tra ciò che è percepito attraverso l'interfaccia riflettente/rifrangente e ciò che è visto in realtà; e la disparità si estende allo spostamento e alla distorsione delle immagini. In entrambi i casi, inoltre, l'immagine è posta all'intersezione tra il raggio incidente e la perpendicolare condotta dall'oggetto alla superficie di riflessione/rifrazione (cioè il cateto). In entrambi i casi, ancora, i punti e le linee radiali pertinenti giacciono su un unico piano; infine, in entrambi i casi, una precisa determinazione della localizzazione dell'immagine dipende, in ultima analisi, da una precisa determinazione della relazione tra i e r.
Nell'opera di Tolomeo la conferma induttiva della legge degli angoli uguali nella riflessione e il tentativo di determinare la relazione tra i e r nella rifrazione si basano entrambi sull'esperimento; è indubbio, però, che la sua procedura sperimentale e i risultati da essa prodotti siano stati condizionati dalle aspettative teoriche di Tolomeo, dato che egli riteneva che la rifrazione fosse un caso speciale di riflessione. Tolomeo, quindi, anticipò l'idea che la relazione tra i e r nella rifrazione sarebbe stata simile, ma non identica, a quella nella riflessione; in altre parole, fra le due relazioni non vi sarebbe stata un'uguaglianza, ma una qualche forma di proporzionalità diretta.
L'interesse di Tolomeo per la rifrazione non era soltanto teorico; infatti la distorsione provocata dalla rifrazione è un fenomeno che ha risvolti pratici, specialmente in astronomia, dove il suo effetto di disturbo delle osservazioni celesti non è poco significativo. In realtà, Tolomeo non fu il primo a collegare la distorsione provocata dalla rifrazione a tali effetti. Strabone (prima del 60 a.C.-20 d.C. ca.) e Cleomede (forse 150-200 ca.) facevano ricorso alla rifrazione per spiegare perché i corpi celesti appaiano significativamente ingranditi sull'orizzonte (la già menzionata 'illusione della Luna'). A loro modo di vedere, la ragione risiede nel fatto che, nel procedere verso l'esterno, i raggi visivi devono passare attraverso l'atmosfera, che è densa e piena di vapore; in queste condizioni, gli oggetti che si trovano al di là dello strato atmosferico appariranno ingranditi, come se fossero immersi nell'acqua. Nell'Almagesto (I.3) anche Tolomeo seguì questa strada, spiegando l'ingrandimento dei corpi celesti all'orizzonte sulla base della rifrazione atmosferica, anche se, al tempo in cui scrisse l'Ottica, egli era consapevole del fatto che tale ingrandimento è apparente, non reale, e dunque indotto psicologicamente piuttosto che fisicamente. In ogni caso, nonostante questa correzione delle precedenti idee sbagliate sull''illusione della Luna', molti pensatori di epoca successiva continuarono a collegarla alla rifrazione atmosferica.
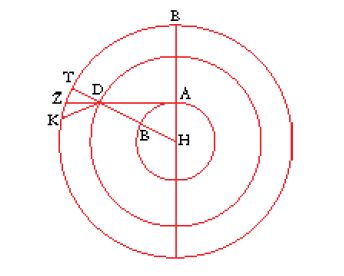
Anche se non causa distorsioni percepibili della dimensione, la rifrazione atmosferica ha però un effetto sulla localizzazione apparente, un fatto che fu chiaramente riconosciuto da Cleomede - il quale notò una differenza tra le posizioni previste e quelle osservate di una stella all'orizzonte - nonché da Tolomeo, che cercò di spiegarla in maniera esauriente nel corso della sua analisi complessiva della rifrazione nel Libro V dell'Ottica. In termini generali, Tolomeo ci informa che la posizione apparente di tutti i corpi celesti rispetto all'orizzonte è spostata verso l'alto a causa della rifrazione atmosferica; ne risulta che, quando questi corpi sono osservati all'orizzonte, in realtà essi giacciono sotto di esso e più si trovano vicini all'orizzonte, maggiore è lo spostamento verso l'alto nella loro localizzazione apparente. Per dimostrare questo fatto, Tolomeo si servì della rifrazione da un mezzo più denso a uno più rado: il cerchio AB nella fig. 13 rappresenta la Terra, ADZ una linea di vista sull'orizzonte e K una stella. Se il punto D è sul confine tra l'atmosfera densa e l'aria (o l'etere) più rada dietro di essa, allora il raggio AD sarà deviato lontano dalla normale TD lungo DK; tuttavia, K sarà visto sul prolungamento DZ del raggio incidente AD e così apparirà più alto di quanto realmente è. Quando la stella si alza sopra l'orizzonte in direzione di E, che è lo zenit di chi guarda, l'entità della deviazione verso l'alto diminuirà costantemente a mano a mano che l'angolo di incidenza si avvicina a 90°, valore per il quale non si ha nessuna rifrazione.
Ciò a cui mira quest'analisi è chiaro: se si può valutare, anche in maniera approssimata, lo spostamento sull'orizzonte causato dalla rifrazione, allora si possono correggere adeguatamente le osservazioni celesti. Tolomeo, però, si preclude questa possibilità, affermando che, senza conoscere la profondità dell'atmosfera rifrangente (compresi aria e fuoco), non si può sperare di pervenire a una ragionevole stima dell'effetto di spostamento. Che, sotto questo aspetto, lo scetticismo di Tolomeo sia strumentale oppure no (e probabilmente non lo è), la rifrazione atmosferica fu praticamente trascurata come problema pratico dagli astronomi successivi fino alla svolta del XVII sec., allorché Tycho Brahe e Giovanni Keplero lo portarono alla ribalta nel tentativo di migliorare l'accuratezza delle osservazioni astronomiche.
L'analisi degli specchi ustori
Nell'Apologia, Apuleio di Madaura fornisce un elenco di argomenti presumibilmente affrontati nel trattato di catottrica da lui attribuito ad Archimede. Dopo aver enumerato sei problemi che riguardano la formazione e la distorsione delle immagini negli specchi, l'elenco si conclude con il "perché gli specchi concavi, se sono tenuti rivolti verso il Sole, incendiano le esche poste nelle vicinanze" e "che cosa fa vedere tra le nuvole archi di diversi colori". Per quanto riguarda Apuleio e la sua presunta fonte, quindi, specchi ustori e arcobaleni formano parte integrante del canone catottrico. Tuttavia, le poche testimonianze testuali che abbiamo per il periodo che va grosso modo dal 300 a.C. al 200 d.C., non sembrano confermarlo. È vero che la Catottrica di Euclide si conclude (in modo piuttosto incongruo) con una proposizione dedicata agli specchi ustori, ma in nessun'altra opera del periodo, o del millennio successivo, l'esame degli specchi ustori o degli arcobaleni è incluso tra gli oggetti generali dell'ottica; la ragione principale del perché ciò non avviene sta probabilmente nel carattere anomalo dei due fenomeni: infatti, mentre da un lato si riteneva che entrambi comportassero riflessione, dall'altro nessuno di essi dà luogo alla formazione di immagini, fenomeno che è il centro dell'attenzione analitica della catottrica antica. Inoltre, nel caso degli specchi ustori sono i raggi luminosi, non quelli visivi, a essere riflessi, e - come si è visto - tra i teorici dell'ottica antichi la luce occupava, nella migliore delle ipotesi, una posizione ambigua.
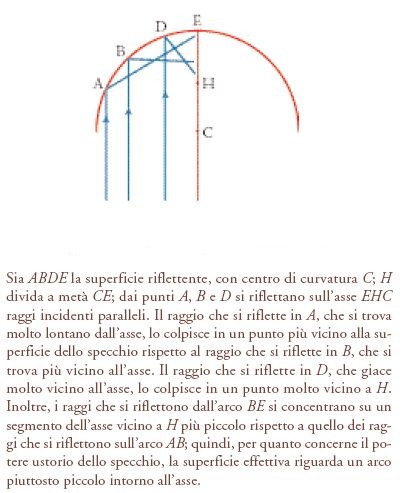
La più antica analisi conosciuta degli specchi ustori si trova nella Catottrica di Euclide, il cui ultimo teorema (prop. 30) è dedicato al potere incendiario degli specchi sferici concavi. In questo teorema Euclide si impegna a stabilire due punti fondamentalmente contraddittori. Il primo è che tutti i raggi luminosi che colpiscono la superficie dello specchio non ad angolo retto, come DA‸X e DB‸X nella fig. 14, si riflettono non nel centro di curvatura C, ma in qualche punto X tra questo e lo specchio. Ciò implica che i raggi di questo non si raccoglieranno, in nessun punto sull'asse, in numero sufficiente per accendere una fiamma. Il secondo punto, in contrasto con il primo, è che i raggi luminosi che passano attraverso il centro di curvatura e colpiscono lo specchio ad angolo retto, come DG, EH e FK, si riflettono indietro verso il centro di curvatura. I raggi di questo tipo, conclude il teorema, non soltanto si riuniscono in numero sufficiente ad accendere una fiamma, ma si riuniscono nel centro di curvatura. Naturalmente questa conclusione è tanto inadeguata quanto semplicistica è la sua giustificazione matematica. Gli specchi sferici concavi non hanno nessun punto focale, tanto meno il centro di curvatura; hanno piuttosto un'area focale rappresentata da un segmento lungo l'asse delimitato dalla superficie dello specchio e da un punto medio rispetto al centro di curvatura. Più vicino all'asse è il punto di riflessione, più vicino al punto medio sarà proiettato sull'asse il raggio riflesso, mentre più lontano dall'asse è il punto di riflessione, più vicino alla superficie dello specchio sarà proiettato sull'asse il raggio riflesso (fig. 15). Per questa ragione gli specchi sferici concavi sono relativamente inefficienti come specchi ustori, anche se possono servire allo scopo se l'esca è posta abbastanza vicina al punto medio H, dove si ha la massima accumulazione di raggi.
Questi fatti sono dimostrati rigorosamente nelle proposizioni 2 e 3 del trattato Sugli specchi ustori di Diocle, la cui distanza cronologica piuttosto ridotta dalla Catottrica di Euclide (circa un secolo) non riflette la notevole distanza nell'analisi tra le due opere. Diocle, infatti, oltre alla trattazione più approfondita degli specchi sferici concavi, fornisce la prima analisi conosciuta della proprietà focale degli specchi parabolici. Innanzitutto dimostra che, in effetti, la parabola fa convergere i raggi paralleli in un unico punto. La dimostrazione è la seguente. FBM (fig. 16) è una parabola con asse ABZ e il segmento BE di quest'asse è uguale alla distanza da B al vertice del cono retto dal quale è generata la parabola; D divide BE in due parti uguali; tutte le linee parallele che colpiscono la parabola, come ST e QR, saranno riflesse in D poiché in tutti questi casi gli angoli di incidenza e di riflessione (le tangenti nei punti di riflessione simulano uno specchio virtuale piano) saranno uguali. Avendo così dimostrato la proprietà focale della parabola, e avendo anche fornito i parametri necessari per determinare la distanza focale, Diocle prosegue sul versante pratico per mostrare come generare una parabola di dimensioni adatte basandosi sulla proprietà che i punti di questa sono equidistanti da un punto (fuoco) e da una retta (direttrice).
Oltre che per la sua priorità cronologica, l'analisi di Diocle degli specchi parabolici è significativa almeno per altre tre ragioni. Innanzitutto, ci sono motivi piuttosto cogenti per supporre che la base di essa risalga ad Archimede e, inoltre, che la scoperta della proprietà focale della parabola, se non il metodo fuoco-direttrice per generarla, sia stata fatta oltre cinquant'anni prima che fosse scritto Sugli specchi ustori. In secondo luogo, il fatto che Apollonio di Perge ometta di occuparsi esplicitamente della proprietà focale delle parabole ‒ il che sembra piuttosto incomprensibile alla luce della sua trattazione della stessa proprietà per ellissi e iperboli ‒ può semplicemente essere un riconoscimento del fatto che un'adeguata dimostrazione c'era già stata per opera di Diocle (che all'incirca era contemporaneo di Apollonio) o di uno dei suoi predecessori. Infine, Diocle offre una giustificazione pratica per la fabbricazione di specchi ustori: se usati nelle cerimonie religiose per immolare vittime sacrificali, essi potevano suscitare meraviglia tra gli astanti ignari. Gli effetti creati con gli specchi, in breve, potevano essere utilizzati per ispirare timore religioso ‒ aspetto, questo, ripreso circa tre secoli dopo da Erone, che dedica due teoremi della sua Catottrica alle illusioni di tipo spettacolare appositamente progettate per l'uso nei templi.
L'analisi dell'arcobaleno
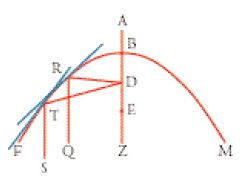
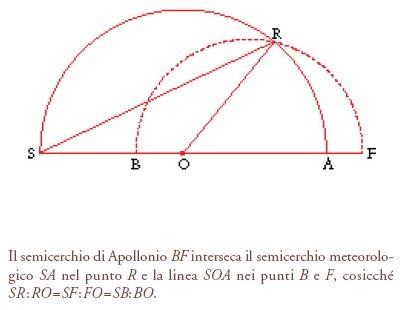
I Meteorologica di Aristotele non rappresentano forse il primo tentativo di dare una spiegazione dell'arcobaleno, ma certamente nell'Antichità è stato quello più elaborato e storicamente più influente. Aristotele, per esempio, sembra abbia seguito tradizioni anteriori nel supporre che l'arcobaleno si crei per riflessione dalle nuvole da pioggia, e la basilare teoria dei colori che la sua spiegazione sottende era lungi dall'essere originale; ciò che la distingue è l'intelaiatura analitica, dal momento che Aristotele sembra essere stato il primo a spiegare sistematicamente l'arcobaleno secondo principî geometrici. Le linee fondamentali della sua analisi sono le seguenti. SRA (fig. 17) rappresenta metà di un cerchio massimo appartenente a quella che è stata chiamata modernamente la 'sfera meteorologica'. SOA rappresenta l'orizzonte; per ragioni pratiche il Sole si trova in S e l'occhio in O. La nuvola responsabile della comparsa dell'arcobaleno si troverà così da qualche parte sull'arco RA, rivolta verso il Sole e l'occhio. Ora, secondo Aristotele, ciò che causa la comparsa dell'arcobaleno è la riflessione dei raggi visivi dalla nuvola che lo fronteggia al Sole; in un certo senso, quindi, l'arcobaleno è semplicemente l'immagine del Sole rispecchiata nella nuvola. Tuttavia, a riflettere l'immagine del Sole non è la nuvola nel suo complesso, ma le singole gocce d'acqua che la compongono. Dal momento che l'immagine si forma in riflettori così minuscoli, del Sole appare soltanto il colore e non la forma; quindi ciò che complessivamente si vede è un insieme di queste minuscole immagini di colore, che formano una fascia ad arco nella nuvola che fronteggia il Sole. Ma che cosa determina la forma e la dimensione di quest'arco? Secondo Aristotele, entrambe dipendono dall'individuazione del punto R di riflessione, che è dove il cosiddetto 'semicerchio di Apollonio' interseca il semicerchio SA. Se, dunque, la linea SOA è presa come asse e se il triangolo SRO è ruotato intorno a esso, l'arco formato da R costituirà il nucleo geometrico dell'arcobaleno, e l'arcobaleno stesso consisterà di una stretta banda di colori disposta su entrambi i lati di questo nucleo. La dimensione dell'arco varierà con la posizione di S, diminuendo continuamente a mano a mano che S si alza sull'orizzonte.
I colori effettivi dell'arcobaleno sono generati secondo la debolezza relativa della luce solare vista all'interno della banda che circonda R. Questa banda si compone di tre colori principali. Il colore che sta più in alto, il rosso, è il più vivido poiché la distanza OR₁S (fig. 18) che il raggio visivo percorre in questo caso è inferiore a ORS, che è a sua volta inferiore a OR₂S. Dunque, più corto è il percorso dei raggi, più forte è l'impressione visiva. Così, l'immagine di colore vista attraverso il punto R₁ appare più intensa di quella vista attraverso il punto R (verde), che appare più intensa di quella vista attraverso il punto R₂ (blu). La comparsa di una quarta tinta, il giallo, tra la banda rossa e quella verde è dovuta, nella concezione di Aristotele, allo schiarimento relativo del rosso che è vicino al più debole verde. Dall'alto in basso, quindi, questo arco è formato da rosso, giallo, verde e blu. Contemporaneamente, a poca distanza, sotto l'arco principale, se ne forma uno secondario che è un'immagine riflessa del primo (cioè, dall'alto in basso, blu, verde, giallo e rosso) e assai meno vivido di quello.
È evidente che questa spiegazione è irta di difficoltà: perché, per esempio, le bande vicine del rosso dell'arco principale e di quello secondario sono separate da una banda scura e non da una chiara, dal momento che, in entrambi i casi, ci dovrebbe essere una progressione verso un colore più vivido? Perché la banda secondaria è invertita? Perché Aristotele basa la sua analisi sui raggi visivi, quando la teoria della visione da lui delineata nel De anima e nel De sensu si basa sull'intromissione? Perché, nella formazione dell'arcobaleno, la maggior parte delle coppie dei raggi di incidenza e di riflessione non rispettano la ragione richiesta dal semicerchio di Apollonio? In ogni caso, nonostante questi problemi, la spiegazione dell'arcobaleno fornita da Aristotele servì ‒ con varie modifiche di alcuni dettagli ‒ come modello per i secoli successivi.
Conclusioni
Per quanto riguarda lo sviluppo teorico, la dottrina classica dei raggi visivi raggiunse il suo culmine verso la fine del II sec. d.C.; che i secoli successivi rappresentino un periodo di semplice assimilazione, se non di arretramento, è indicato dal fatto che nella Tarda Antichità, diversamente dall'Almagesto, l'Ottica di Tolomeo praticamente sembra non essere stata letta, forse perché era troppo avanzata per le necessità che quel pubblico dimostrava di avere. L'ottica, dopo tutto, non era parte integrante del canone delle arti liberali e coloro che ne raccomandavano lo studio ‒ come Vitruvio (attivo verso la fine del I sec. a.C.) e, più tardi, Proclo (attivo verso la metà del V sec. d.C.) ‒ lo facevano più per interessi pratici che teorici. Anche tra le persone colte della Tarda Antichità, il livello della conoscenza e dell'interesse teorico per l'ottica sembra si fosse notevolmente abbassato. Galeno vale come esempio, dal momento che, sebbene si fosse sentito in dovere di dare una descrizione matematica del cono visivo nel Libro X del De usu partium, riconobbe che le conoscenze tecniche che una simile descrizione richiedeva non erano alla portata dei suoi lettori. E, nel decidere di comporre un commentario sull'ottica, Teone di Alessandria fece riferimento, come base testuale, non all'Ottica di Tolomeo, ma al suo più antico antecedente Euclide.
Come per altre discipline scientifiche, anche per l'ottica si ebbe un rinnovato sviluppo nel IX e nel X sec., cioè quando il pensiero greco ed ellenistico fu assimilato da pensatori arabi. Decisiva, in questo senso, fu la riscoperta dell'Ottica di Tolomeo. La trattazione della rifrazione presente nel Libro V spinse Ibn Sahl al-Isrā῾ilī, matematico arabo del X sec., ad affrontare il problema delle lenti ustorie e a formulare correttamente la legge della rifrazione. Analogamente ispirato dall'Ottica, ma su scala più generale, Ibn al-Hayṯam (1039) riesaminò l'intera intelaiatura teorica dell'ottica di Tolomeo. Il risultato, raccolto nel Kitab al-Manazir (Libro dell'Ottica), fu una riconsiderazione a vasto raggio dell'ottica fisica e della teoria della visione secondo un modello intromissionista basato su una radiazione puntiforme indifferenziata.
A tutti gli effetti, la formulazione della teoria intromissionista di Ibn al-Hayṯam e la sua diffusa accettazione da parte dei teorici medioevali, particolarmente nell'Occidente latino, segnò la fine della tradizione classica dei raggi visivi. La scienza dell'ottica trovava ora il suo fondamento fisico nella radiazione di luce e colore piuttosto che nel flusso visivo; uno spostamento dell'analisi, questo, che produsse nella teoria della visione una separazione tra la causa fisica e l'effetto percettivo. Questa separazione fu decisiva per lo sviluppo dell'ottica moderna nel XVII sec., quando i raggi visivi della teoria classica furono interamente trasformati nei raggi luminosi della moderna analisi ottica.
Bibliografia
Beare 1906: Beare, John Isaac, Greek theories of elementary cognition from Alcmaeon to Aristotle, Oxford, Clarendon Press, 1906.
Boyer 1959: Boyer, Carl B., The rainbow from myth to mathematics, New York, T. Yoseloff, 1959.
De Pace 1981-82: De Pace, Anna, Elementi aristotelici nell’Ottica di Claudio Tolomeo, “Rivista critica di storia della filosofia”, 36, 1981, pp. 123-138; 37, 1982, pp. 243-276.
Knorr 1985: Knorr, Wilbur R., Archimedes and the pseudo-euclidean catoptrics. Early stages in the ancient geometric theory of mirrors, “Archives internationales d’histoire des sciences”, 35, 1985, pp. 27-105.
– 1994: Knorr, Wilbur R., Pseudo-Euclidean reflections in ancient optics, “Physis”, 31, 1994, pp. 1-45.
Lejeune 1948: Lejeune, Albert, Euclide et Ptolémée, deux stades de l’optique géométrique grecque, Louvain, Bibliothèque de l’Université, 1948.
– 1957: Lejeune, Albert, Recherches sur la catoptrique grecque d’après les sources antiques et médiévales, Bruxelles, Palais des Académies, 1957.
Lindberg 1976: Lindberg, David C., Theories of vision from Al-Kindi to Kepler, Chicago, University of Chicago Press, 1976.
Rashed 1990: Rashed, Roshdi, A pioneer in anaclastics: Ibn Sahl On Burning Mirrors, “Isis”, 81, 1990, pp. 464-491.
Saint-Pierre 1972: Saint-Pierre, Bernard, La physique de la vision dans l’antiquité. Contribution à l’établissement des sources anciennes de l’optique médiévale, unpublished Ph. Diss., University of Montréal, 1972.
Simon 1988: Simon, Gérard, Le regard, l’être et l’apparence dans l’optique de l’antiquité, Paris, Éditions du Seuil, 1988.
– 1992: Simon, Gérard, L’Optique d’Ibn al-Haytham et la tradition ptoléméenne, “Arabic sciences and philosophy”, 2, 1992, pp. 203-235.
Smith 1981: Smith, A. Mark, Saving the appearances of the appearances. The foundations of classical geometrical optics, “Archive for history of exact sciences”, 24, 1981, pp. 73-99.
– 1982: Smith, A. Mark, Ptolemy’s search for a law of refraction. A casestudy in the classical methodology of saving the appearances and its limitations, “Archive for history of exact sciences”, 26, 1982, pp. 221-240.
– 1988: Smith, A. Mark, The psychology of visual perception in Ptolemy’s Optics, “Isis”, 79, 1988, pp. 189-206.
Solmsen 1961: Solmsen, Friedrich, Greek philosophy and the discovery of the nerves, “Museum Helveticum”, 18, 1961, pp. 150-197; ora in: Solmsen, Friedrich, Kleine Schriften, Hildesheim, G. Olms, 1968, 3 v.; v. I, pp. 536-582.
Stratton 1917: Stratton, George Malcolm, Theophrastus and the Greek physiological psychology before Aristotle, London, G. Allen & Unwin, 1917.