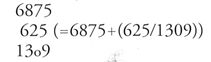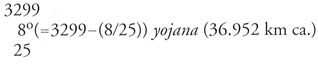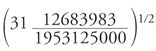Scienza indiana: periodo classico. Matematica

Scienza indiana: periodo classico. Matematica

Matematica

'Gaṇita' ('matematica')

Prima dell'introduzione e diffusione dell'astrologia oroscopica e dell'astronomia matematica nella società indiana, l'occupazione che più di ogni altra richiedeva calcoli era probabilmente quella del contabile. Questo infatti veniva detto gaṇaka o saṃkhyāyaka, termini sanscriti traducibili entrambi con 'colui che calcola', 'calcolatore'. Nel Mahābhārata (Grande poema dei Bhārata; 2.5.62), il saggio Nārada raccomanda al re Yudhiṣṭhira di richiedere ogni mattina un resoconto dettagliato delle entrate e delle spese al calcolatore (gaṇaka) e allo scriba (lekhaka). Anche l'Arthaśāstra (Trattato sull'utile) di Kauṭilya (1.19.9) fa riferimento a questo impegno quotidiano del re. Il calcolatore e lo scriba di un re ricevono ciascuno uno stipendio di 500 paṇa, mentre lo stipendio più alto, 48.000 paṇa, è corrisposto a un ministro, a un principe, ecc., e il più basso, 60 paṇa, a un servo che si occupa di accudire gli animali (ibidem, 5.3.3-17). I sovrintendenti ai dipartimenti governativi sono assistiti da cinque funzionari: calcolatori, scribi, ispettori delle monete (rūpadarśaka), tesorieri (nīvīgrāhaka) e supervisori (uttarādhyākṣa) (ibidem, 2.9.28). Secondo un testo giuridico posteriore, la Bṛhaspatismṛti (Codice tradizionale di Bṛhaspati; 1.1.81-90), una corte consta di dieci funzionari, fra cui il gaṇaka, che conta il denaro e fa l'inventario dei beni, e il lekhaka, che scrive le sentenze.

Nel Kalpasūtra (Scrittura sul rituale monastico; 1.61) jaina di Bhadrabāhu, opera in lingua ardhamāgadhī, un gaṇaga (in sanscrito, gaṇaka) figura tra gli attendenti del re Siddhārtha. Si narra che la moglie di questi, Triśālā, avesse ricevuto nel suo grembo il feto di Mahāvīra (fondatore della religione jaina) da Devānandā, moglie del brahmano Ṛṣabhadatta.

Anche in alcuni testi del Canone buddhista, composto in lingua pāli, si fa riferimento a calcolatori (gaṇaka) e a 'ministri-calcolatori' (gaṇaka-mahāmātra).

Il racconto 107 del Majjhimanikāya (Mucchio dei discorsi medii), il Gaṇakamoggallānasutta (Discorso dell'esperto di calcoli Moggallāna), narra di una conversazione tra il Buddha e un gaṇaka brahmano di nome Moggallāna, dalla quale apprendiamo che un gaṇaka si guadagnava da vivere eseguendo calcoli (gaṇanā), aveva allievi residenti presso di lui ai quali insegnava il calcolo (saṅkhāna), e per prima cosa a contare da uno a cento. In questo racconto i termini, in lingua pāli, gaṇanā e saṅkhāna (in sanscrito, saṃkhyāna) sembrano designare rispettivamente il calcolo in generale ‒ come dire la matematica ‒ e un calcolo di tipo relativamente elementare che ha inizio con il contare. La gaṇanā ('abilità nel far calcoli') in questione è presumibilmente la stessa dell'episodio di Upāli narrato in una sezione del Vinayapiṭaka (Cesta della disciplina), il Mahāvagga (Sezione dei testi estesi; 1.49.1-2), in cui è indicata come una delle tre competenze che consentono di guadagnarsi da vivere (le altre sono lekha, 'scrittura', e rūpa, 'ispezione delle monete'). Secondo l'iscrizione della grotta di Hāthīgumphā, queste tre arti, insieme a vyavahāra ('giurisprudenza') e vidhi ('riti religiosi'), costituivano le cinque materie che il re Khāravela (II o I sec. a.C.) studiò tra i sedici e i ventiquattro anni di età.

La differenza tra gaṇanā e saṅkhāna non è sempre chiara. Nelle opere del Canone buddhista essi ricorrono più volte insieme a muddā (in sanscrito, mudrā) per designare le tre tecniche di calcolo. Secondo l'Avyākaṭasaṃyutta (Testo coordinato sulle [questioni] non definite; 1.13-14) del Saṃyuttanikāya (Mucchio dei testi interconnessi; 44), un re usava esperti di tre tecniche di calcolo: gaṇaka, muddika e saṅkhāyaka. Il termine muddā, che in genere significa 'gesto delle dita' oppure 'sigillo', in questa triade potrebbe avere il significato di 'indigitazione', cioè dell'arte di contare servendosi delle dita delle due mani, ma non sembrano esservi altre prove del fatto che questa tecnica fosse in uso nell'India antica.

Nel Lalitavistara (Descrizione estesa dei giochi [del Buddha]; cap. 12), opera in sanscrito del primo buddhismo mahāyāna (scuola del 'Grande veicolo'), un ministro-calcolatore di nome Arjuna assiste in qualità di testimone a una competizione di 'calcolo numerico' (saṃkhyā-gaṇanā) e rimane stupefatto dall'abilità di un bodhisattva.

Secondo l'Arthaśāstra (1.2-5), un principe apprende la scrittura (lipi) e il calcolo (saṃkhyāna) dopo il rito della tonsura e quindi, dopo l'iniziazione, le quattro discipline (vidyā), cioè la filosofia, i Veda con le materie correlate, le conoscenze pratiche, quali l'agricoltura e il commercio, e la politica. Questo saṃkhyāna è elementare quasi quanto il saṅkhāna di Moggallāna, anche se nell'Arthaśāstra un calcolatore è generalmente definito saṃkhyāyaka, e non gaṇaka.

Nel Mahābhārata (3.70), il re Ṛtuparṇa si mostra orgoglioso della propria abilità nel saṃkhyāna, oltre che nel gioco dei dadi, poiché riesce a dare una stima corretta del numero di noci, 2095, che si trovano su due rami di un albero di vibhītaka (Terminalia bellerica). Saṃkhyāna implica, quindi, anche una sorta di stima statistica delle quantità di noci, di raccolto, e così via.

La parola che in seguito avrebbe comunemente designato la scienza matematica non è però né gaṇanā, né saṃkhyāna, bensì gaṇita; questo termine sanscrito trae probabilmente origine dalla parola gaṇiya, usata nei testi canonici jaina composti in lingua ardhamāgadhī. Si narra che il primo tīrthaṅkara ('facitore del guado') jaina, Ṛṣabha, abbia insegnato le 72 arti, le 64 virtù femminili, le 100 arti manuali e le tre opere. Secondo l'opera jaina Samavāyaṅga (Il membro delle combinazioni; 72), le prime tre delle 72 arti sono leha, gaṇiya e rūva, corrispondenti rispettivamente a lekha, gaṇanā e rūpa ('scrittura', 'calcolo' e 'ispezione delle monete') dei testi canonici buddhisti. Il termine gaṇiya compare anche, per esempio, nel Ṭhāṇaṅga (Il membro delle possibilità; 716) assieme a bhaṃga ('calcolo combinatorio'), respiro, fiori, amore, ecc., in una lista dei dieci elementi sottili.

Nell'Arthaśāstra (2.7.10, 2.21.15), l'inventario delle merci è chiamato gaṇita. Nel Mahābhārata (1.2.19), coloro i quali sono capaci di usare la regola del tre sono chiamati 'coloro che sanno la verità della saṃkhyā ('numero') e del gaṇita'. Śūdraka, autore della Mṛcchakaṭikā (Carretto d'argilla, IV o V sec. d.C.), dice di aver appreso il Ṛgveda (Veda degli inni), il Sāmaveda (Veda dei canti), il gaṇita, le arti e la scienza degli elefanti (ibidem, 1.4).

Āryabhaṭa I, nel primo verso dell'Āryabhaṭīya (Trattato di Āryabhaṭa, 499 d.C. o poco più tardi), elenca i tre argomenti di cui tratterà nei capitoli successivi, ossia gaṇita, kāla-kriyā ('misura del tempo') e gola ('geometria sferica').

I numerali

I numerali vedici (v. cap. VI, par. 1) continuarono a essere usati nella società hindu dei secoli successivi; buddhisti e jaina, invece, elaborarono sistemi propri per i numeri maggiori di mille. Il sistema buddhista è basato sul sistema centesimale, che è analogo a quello decimale ma ha per base cento anziché dieci e prevede quindi l'introduzione di un nuovo termine per ogni multiplo di cento; se 10ⁿ (dove n è un numero dispari maggiore di 6 o 8) si chiama x, 10ⁿ⁺¹ è detto mahā-x ('grande x'). Il sistema jaina è invece sulla base di diecimila. Da mille (sahassa) in su si hanno 'dieci sahassa', 'cento sahassa' e 'dieci-cento sahassa'. Analogamente, da koḍi (10⁷) in su si hanno 'dieci koḍi', e così via.

A parte la scrittura della civiltà dell'Indo, la più antica scrittura indiana conosciuta è la kharoṣṭhī, probabilmente di origine aramaica; il suo uso restò circoscritto all'India nordoccidentale e all'Asia centrale tra il IV sec. a.C. e il IV d.C. Nel III sec. a.C. comparve negli editti dell'imperatore Aśoka un'altra scrittura chiamata brāhmī, prototipo di numerose scritture dell'Asia meridionale e sudorientale. Il suo rapporto con la kharoṣṭhī non è certo. Queste scritture avevano i propri simboli numerici e usavano segni particolari non soltanto per le unità ma anche per le decine, le centinaia, le migliaia, e così via; alcuni di questi simboli e segni erano ottenuti per addizione, altri per moltiplicazione, e in nessuna delle due scritture i sistemi numerici erano di tipo posizionale. I numerali della brāhmī restarono in uso nell'epigrafia anche dopo i primi secoli dell'era cristiana, quando nei calcoli quotidiani e nella letteratura matematica fu introdotto il sistema di numerazione posizionale.

La testimonianza più antica sull'uso del sistema decimale posizionale in India è fornita dallo Yavanajātaka (Oroscopia secondo gli Occidentali, 269-270 d.C.) di Sphujidhvaja, un testo di astrologia che nelle strofe del colophon (79.60-62) esprime gli anni 71 e 191 dell'era Śaka con le seguenti parole a valore numerico: viṣṇu(1)-graha(7) e nārāyaṇa(1)-aṅka(9)-indu(1). È questo il primo esempio di notazione dei numeri mediante parole, basata su associazioni naturali e culturali fra cose e numeri come 'Luna' e 1, 'occhio' e 2, 'fuoco' e 3, ecc. (la corrispondenza non è biunivoca). Le parole-numero sarebbero diventate molto comuni nei testi matematici di epoca più tarda, soprattutto in campo astronomico.

Nell'Aṇuogaddāra (Le porte della disquisizione; 423), testo jaina del III-V sec. d.C., si parla di un numero che occupa 29 'posizioni' (ṭhāṇa) decimali. Nell'Abhidharmakośabhāṣya (Commento al tesoro dell'Abhidharma; 5.26) il buddhista Vasubandhu, vissuto nel IV o nel V sec. d.C., usa come metafora una sorta di abaco, in cui un dischetto ha il valore di un'unità, una decina, un centinaio, ecc., a seconda del posto in cui lo si fa rotolare; il brano in questione compare nel contesto di una teoria filosofica attribuita a Vasumitra, probabilmente del I o II sec. d.C. Lo stesso testo (3.93-94), nel definire il numerale asaṃkhya (=10⁵⁹), dà i nomi di 60 'posizioni' (sthāna) decimali. Āryabhaṭa (nato nel 476 d.C.), definendo la propria notazione alfabetica dei numeri (Āryabhaṭīya, 1.2), usa il termine kha ('cielo' o 'posto mancante' o 'spazio') per le posizioni della notazione e, nella stessa accezione, il termine sthāna quando elenca i nomi di 10 posizioni decimali (ibidem, 2.2); la regola per l'estrazione delle radici quadrate e cubiche (ibidem, 2.4-5) si basa sul sistema posizionale.

L'associazione di aṅka ('segno') e 9 nell'esempio precedente tratto dallo Yavanajātaka mostra chiaramente che in queste espressioni verbali il sistema decimale posizionale si basa su 9 simboli e non comprende lo zero; quest'ultimo è dunque escluso dal concetto di aṅka, qui come nella matematica indiana posteriore.

Non sappiamo se la numerazione decimale posizionale indiana prevedesse sin dagli inizi un simbolo per lo zero, che non tutte le numerazioni posizionali avevano, come dimostra la notazione sessagesimale antico-babilonese, ma mancano riferimenti allo zero nello Yavanajātaka. Nel Chandaḥsūtra (Aforismi sulla metrica; 8.28-31) di Piṅgala, opera sulla prosodia sanscrita, lo zero (śūnya) e il due (dvi) sono usati come segni, rispettivamente, della moltiplicazione per due e dell'elevazione al quadrato nel calcolo delle potenze di due che compaiono nel membro destro dell'uguaglianza 2+2²+2³+…+2ⁿ=2×2ⁿ−2. La datazione di quest'opera è controversa, in quanto per alcuni è del 200 a.C., per altri del III sec. d.C. o più tardi. La più antica testimonianza dello zero sia come simbolo sia come numero si trova nella Pañcasiddhāntikā (Esposizione dei cinque siddhānta) di Varāhamihira (550 d.C. ca.).

La matematica dei jaina

Nei secoli a cavallo dell'era cristiana i jaina ebbero un ruolo di grande rilievo nello sviluppo della matematica indiana e ciò si spiega, almeno in parte, con il rigore religioso e il perfezionismo loro propri. La parte riguardante la matematica (saṅkhāna) del Ṭhāṇaṅga (Il membro delle possibilità), testo canonico jaina (in lingua ardhamāgadhī) del 747 d.C., consta di dieci argomenti, che presumibilmente abbracciano tutta la matematica nota agli Indiani dell'epoca. Essi sono: il calcolo di base (parikamma), procedimenti, ossia matematica per usi pratici (vyavahāra), la corda (rajju), la quantità (rāsi), la riduzione di frazioni (kalāsavanna), 'tanti quanti' (jāvaṃtāvati), il quadrato (vagga), il cubo (ghana), il quadrato del quadrato (vaggavagga) e modi di scegliere (vikappa, 'calcolo combinatorio'). Il contenuto di questi argomenti non è però specificato. I primi due capitoli ricordano le due parti principali della pāṭī (termine corrispondente al moderno 'algoritmo'), uno dei due campi principali della matematica indiana posteriore (l'altro è la bīja-gaṇita, 'matematica dei semi', concernente le equazioni algebriche); il terzo e il quarto, probabilmente da considerare in coppia, indicano rispettivamente la 'matematica delle figure' (kṣetra-gaṇita) e la 'matematica delle quantità' (rāśi-gaṇita); gli argomenti dal sesto al nono richiamano i nomi di quattro tipi di equazioni menzionate da Bhāskara I (attivo nel 629 d.C.), ma il loro significato non è chiaro.

Le conoscenze geometriche ebbero un ruolo determinante nella cosmografia jaina, che ha una forte impronta numerica rispetto a quella hindu e buddhista. Secondo opere jaina di cosmografia del V-VI sec., come la Jaṃbuddīvapaṇṇattī (Esposizione del Jaṃbudvīpa, V sec. d.C. o prima), tradizionalmente attribuita a Mahāvīra (morto nel 480 a.C. ca.), e la Tiloyapaṇṇattī (Esposizione dei tre mondi) di Jadivasaha (600 d.C. ca.), lo 'spazio del mondo', che avrebbe la forma di tre tronchi di cono (secondo la setta Śvetāmbara) o di tre prismi (secondo i Digambara) sovrapposti, è circondato dall'infinito 'spazio del non mondo'. Lo 'spazio del mondo' è suddiviso in tre 'mondi', superiore, medio e inferiore, e al centro del mondo medio è situato un continente circolare chiamato Jambūdvīpa (in ardhamāgadhī, Jaṃbuddīva), suddiviso in 7 regioni da 6 catene montuose parallele con orientamento est-ovest. Al centro di questo sorge il monte Meru, che è l'asse dell'Universo, mentre la regione più meridionale, a forma di arco, è Bhārata, ossia l'India. Jambūdvīpa è circondato da un numero infinito di oceani alternati a continenti che sono a forma di anelli concentrici.

I jaina calcolavano lunghezza di linee, aree di superfici, volume e inclinazione di diverse parti dello 'spazio del mondo'. Come valore di π usavano la radice quadrata di 10, cioè 10^1/2, oppure 3 (sull'origine di 10^1/2, v. Gupta 1986). Le loro formule relative al cerchio e alla sfera comprendono: c=(10d²)^1/2, A=c(d/4), V=9(d/2)³/2, a=[4(d−h)h]^1/2, b=(a²+6h²)^1/2, B=(10^1/2ah)/4, dove d, c e A sono, rispettivamente, diametro, circonferenza e area del cerchio, V il volume della sfera di diametro d, e a, b, h, e B sono, rispettivamente, la corda, l'arco, l'altezza (di solito chiamata 'profondità' o 'freccia') e l'area di un settore circolare. Per la radice quadrata di un numero non quadrato, usavano la formula approssimata (a²+r)^1/2≈a+[r/(2a)]. Per esempio, la circonferenza del continente circolare Jambūdvīpa, il cui diametro è di 10⁵ yojana (unità di lunghezza equivalente a 11,22 km ca.), era calcolata nel modo seguente: (10×10¹⁰)^1/2 = (316.227²+484.471)^1/2≈316.227+484.471/(2×316.227) yojana e la parte frazionaria era espressa in unità di lunghezza più piccole.

Il calcolo combinatorio è uno dei settori della matematica prediletti dagli Indiani. Era usato in diversi campi al di fuori della matematica: religione, filosofia, prosodia, musica, architettura, astrologia e medicina. Come si è detto, un trattato canonico jaina lo includeva nella matematica. La Viyāhapaṇṇattī (Esposizione sui conflitti [dei pianeti]; 9.32), per esempio, elenca i vari modi in cui un essere vivente, due esseri viventi, …, dieci esseri viventi, esseri viventi numerabili e non numerabili possono essere distribuiti nei sette inferni. In un altro brano (8.5) è correttamente indicato in 49 il numero di modi di scegliere, da due gruppi di tre oggetti ciascuno, un insieme contenente almeno un oggetto di ciascun gruppo.

Gli Indiani conoscevano inoltre la regola degli esponenti. L'Aṇuogaddāra (Le porte della disquisizione; 423), per esempio, esprime il numero N di tutti gli esseri umani in quattro modi. Tre di questi sono: (1) N occupa 29 posizioni decimali; (2) N è uguale 'al quadrato sesto di due moltiplicato per il quadrato quinto di due', ossia 2⁽²⁶⁾×2⁽²⁵⁾; (3) N 'è divisibile per due 96 volte'. Dalla definizione (2) si ha allora: N=2⁽²⁶⁾×2⁽²⁵⁾=2⁶⁴×2³²=2⁹⁶=79.228.162.514.264.337.593.543.950.336, che dimostra le definizioni (1) e (3).

I jaina misero a punto un elaborato sistema di numeri, distinguendo tra numeri 'numerabili' (saṃkhyeya), 'non numerabili' (asaṃkhyeya) e 'infiniti' (ananta), sistema che fu usato nella loro ontologia. Secondo l'Aṇuogaddāra (497-519), l'insieme dei numeri non numerabili è suddiviso in tre sottoinsiemi, cioè numeri 'restrittivamente non numerabili', 'propriamente non numerabili' e 'non numerabilmente non numerabili'; analogamente, l'insieme dei numeri infiniti è suddiviso in tre sottoinsiemi, cioè numeri 'restrittivamente infiniti', 'propriamente infiniti' e 'infinitamente infiniti'. L'insieme dei numeri numerabili comincia con 2 (poiché non si può 'contare' se si ha un solo oggetto) e termina col numero minore, diciamo a, dell'insieme dei numeri restrittivamente non numerabili, meno uno. Il numero a è ottenuto mediante un procedimento immaginario che consiste nel riempire di semi di senape bianca quattro granai di diametro pari al diametro del Jambūdvīpa (10⁵ yojana) e di altezza pari alla centesima parte di questo; il numero a si può considerare un analogo dell''aleph zero', il più piccolo numero cardinale transfinito della matematica moderna. Il più piccolo numero di ciascuno degli altri sottoinsiemi è dato, rispettivamente, da a^a, b^b con b=(a^a)², c^c con c=b^b, d^d con d=c^c, ed e^e con e=(d^d)², mentre il più grande, escluso l'insieme dei numeri infinitamente infiniti per il quale non esiste un massimo, è dato dal più piccolo numero del sottoinsieme successivo meno uno.

I secoli V e VI: gli inizi

Āryabhaṭa I

Āryabhaṭa I è così chiamato per distinguerlo da un astronomo omonimo, Āryabhaṭa II, autore del Mahāsiddhānta (Grande siddhānta). Āryabhaṭa I è considerato uno dei più influenti matematici e astronomi dell'India grazie a due opere, l'Āryabhaṭīya (Trattato di Āryabhaṭa) e l'Āryabhaṭasiddhānta (Siddhānta di Āryabhaṭa). Quest'ultimo testo non si è conservato, ma è menzionato da Varāhamihira (VI sec.) di Avantī (l'odierna Ujjain) e usato da Bhāskara I di Valabhī (presso l'attuale Bhāvnagar), che ne riporta gli elementi fondamentali nel cap. 7 del Mahābhāskarīya (Trattato esteso di Bhāskara), e da Brahmagupta di Bhillamāla (capitale dei Gurjara), autore del Khaṇḍakhādyaka (Bocconcini, 665 d.C.), basato sul 'sistema della mezzanotte' dell'Āryabhaṭasiddhānta, in cui il giorno civile era calcolato da una mezzanotte a quella successiva. L'opera in questione influenzò principalmente l'India nordoccidentale. È noto inoltre che contribuì allo sviluppo dell'astronomia sasanide e islamica. L'Āryabhaṭīya, invece, godette di notevole popolarità soprattutto nell'India meridionale, dove fu commentato sia in sanscrito sia in lingua telugu; il più antico commento conosciuto è quello di Bhāskara I (629 d.C.).

Āryabhaṭa I nacque nel 476, come dichiara egli stesso nell'Āryabhaṭīya (3.10): "Quando erano passati sessanta volte sessant'anni e tre quarti dello yuga, erano trascorsi ventitré anni dalla mia nascita". Aveva cioè 23 anni nel 499 d.C. (come si evince calcolando 3600−3101, poiché l'ultimo quarto, chiamato kaliyuga, dello yuga iniziò nel 3102 a.C.); l'anno in questione, il 499 d.C., è di solito considerato la data di composizione dell'Āryabhaṭīya.

All'inizio del cap. 2 afferma di "riportare qui [in questo libro] le conoscenze rispettate a Kusumapura". Kusumapura, 'Città dei fiori', è stata identificata con Pāṭaliputra (presso l'odierna Patna), capitale dell'Impero dei Gupta, dove è possibile che Āryabhaṭa abbia lavorato. Egli non rivela il suo luogo di nascita, ma Bhāskara I lo definisce 'un uomo dell'Aśmaka'; si deve dunque presumere che Āryabhaṭa nacque nell'Aśmaka, regione situata tra i fiumi Godavari e Narmada (Āryabhaṭīya, ed. Shukla).

L'Āryabhaṭīya è suddiviso in quattro 'quarti' (pāda) così intitolati: (1) Quarto in dieci versi gīti; (2) Quarto sulla matematica (gaṇita; in 33 versi āryā); (3) Quarto sulla misura del tempo (kālakriyā; in 25 versi āryā); (4) Quarto sulla geometria sferica (gola; in 50 versi āryā).

Il primo capitolo e gli altri tre sono a volte considerati come due opere indipendenti. Infatti il cap. 1, che consta di tabelle di dati numerici, si può considerare un supplemento alla seconda parte (capp. 2-4), che invece fornisce numerose regole per le tre materie trattate. Ciascuna parte ha un verso introduttivo e uno conclusivo; il metro usato nella prima è la gīti, nella seconda l'āryā. I numeri sono espressi in notazione alfabetica nella prima parte, con numerali ordinari nella seconda. Anche il fatto che la seconda parte consti di 108 versi āryā sembra confermarne l'indipendenza (il numero 108, come il 18 e il 1008, è sacro per gli Indiani). Il cap. 1 consta di 13 versi. Nel primo verso l'autore rende omaggio al dio Brahmā e menziona l'argomento dei tre capitoli successivi. Il v. 2 espone un sistema di notazione alfabetica dei numeri. I dieci versi successivi (a cui si riferisce il titolo del capitolo) contengono tabelle di parametri astronomici e di differenze di seni espresse in quella notazione; per esempio, il numero delle rivoluzioni del Sole nello yuga, 4.320.000, è espresso come khyughṛ=(2+30)×10⁴+4×10⁶. L'ultimo verso è dedicato a un commento conclusivo.

Il cap. 2 dell'Āryabhaṭīya è, dopo gli Śulbasūtra (Aforismi sulla costruzione di altari), il più antico testo matematico sanscrito che ci sia pervenuto. Non presenta una chiara suddivisione interna ma può essere ripartito in quattro sezioni: (1) regole per il calcolo di base (vv. 2-5); (2) regole per le figure geometriche (vv. 6-18); (3) regole per le figure e le quantità (vv. 19-24); (4) regole per le quantità numeriche (vv. 25-33).

Āryabhaṭa dà i nomi delle prime posizioni decimali, e dice: "[Ciascuna] posizione è dieci volte più grande della posizione [precedente]" (v. 2). I nomi sono basati sui primi otto nomi della numerazione non posizionale vedica (cap. VI, par. 1), discostandosene soltanto negli ultimi tre termini. Per la posizione di 10⁷ introduce la denominazione koṭi, già usata nelle tradizioni non vediche, spostando arbuda alla posizione successiva. È degno di nota che Āryabhaṭa I conservi ancora il termine vedico niyuta per 10⁵, che sarà sostituito dal termine lakṣa delle tradizioni non vediche negli elenchi dei matematici posteriori.

La regola di Āryabhaṭa per l'estrazione della radice quadrata è la seguente: "Si divida la [posizione] non quadrata [ossia quella non pari] per due volte la radice quadrata [contenuta in essa]. Mentre il quadrato [del quoziente] è sottratto dalla [posizione] quadrata [cioè, dispari], il quoziente è [abbassato] alla posizione (sthāna) successiva come [parte della] radice quadrata" (Āryabhaṭīya, 2.4).

Espressioni estremamente concise di questo tipo sono caratteristiche degli antichi matematici indiani, che attribuivano molta importanza alla trasmissione orale (sampradāya); quest'ultima avrebbe supplito alla concisione dei testi.

Per il cerchio, egli dà l'area come prodotto della semicirconferenza per la metà del diametro (v. 7) e il valore del rapporto tra circonferenza e diametro, cioè π (=3,141592…), come (62.832):(20.000)=3,1416 (v. 10), di gran lunga migliore del valore 10^1/2 (=3,1622…) dei jaina, all'epoca prevalente. Non sappiamo in quale modo Āryabhaṭa l'abbia ottenuto. Secondo alcuni l'avrebbe ricavato da solo a partire da poligoni regolari inscritti e circoscritti o anche soltanto inscritti (Sengupta 1927; Sarasvati Amma 1979). Altri invece postulano un influsso greco (Toomer 1973; van der Waerden 1983) o cinese (Qian 1990).

Dopo aver stabilito che la corda che sottende un arco pari a un sesto della circonferenza di un cerchio è uguale al raggio (v. 9b), Āryabhaṭa enuncia un principio per ottenere 'mezze corde', cioè seni, in un quarto di cerchio: "Si divida un quarto della circonferenza di un cerchio 'uniforme' per mezzo di triangoli e quadrilateri [in modo da ottenere] sul semidiametro dato tanti seni quanti se ne desiderano" (v. 11). Secondo i suoi commentatori, a cominciare da Bhāskara I, quello che s'intende presentare in questo passo è un metodo chiamato 'produzione del seno' (jyā-utpatti) o 'procedimento grafico' (chedyaka-vidhi), esplicitamente enunciato da Varāhamihira e altri. La trigonometria, comprendente tavole di seni, risulta essere uno dei più utili strumenti per l'astronomia indiana.

Un altro prezioso strumento per l'astronomia era il calcolo basato sulla proporzionalità fra i lati di triangoli rettangoli simili. Rientrano in questa categoria i problemi relativi allo gnomone e alla sua ombra (vv. 14-16). Si tratta naturalmente di casi particolari di proporzione (v. oltre).

Il teorema di Pitagora è così espresso da Āryabhaṭa: "Il quadrato del braccio (base, a) e il quadrato della verticale (b) costituiscono insieme il quadrato dell'orecchio (ipotenusa, c)" (v. 17a), vale a dire a²+b²=c². Quest'espressione si colloca tra quella degli Śulbasūtra, dove è data in termini puramente geometrici, senza la parola 'quadrato (numerico)' (varga), e quella delle opere matematiche posteriori, a cominciare dal Brāhmasphuṭasiddhānta (Siddhānta corretto di Brahmagupta), in cui il modo di calcolarla è il seguente: c=(a²+b²)^1/2.

Āryabhaṭa fornisce dunque regole e formule corrette per figure piane, mentre sono errate le formule per il volume V del tetraedro (v. 6), V=(A/2)×h, in cui A è l'area della base e h l'altezza, e della sfera (v. 7), V=A(A)^1/2, in cui A è l'area di un cerchio massimo.

Āryabhaṭa dà anche formule corrette per somme di progressioni aritmetiche, successioni di numeri naturali, serie di quadrati e di cubi (vv. 19-22), ma non parla di progressioni geometriche. Dati

A(n)  =a+(a+d)+(a+2d)+...+[a+(n-1)d],

S(n)  =1+2+...+n,

S₂(n) =S(1)+S(2)+...+S(n),

Sⁱ(n) =lⁱ+2ⁱ+...+nⁱ (per i=2, 3),

le formule di Āryabhaṭa sono:

A(k+n)-A(k)=n{a+[k+(n-1)/2]d}=(a_k+1+a_k+n)n/2,

n =[{[8dA(n)+(d-2a)²]^1/2-2^a}/d+1]/2,

S₂(n) =n(n+1)(n+2)/6=[(n+1)³-(n+1)]/6,

S²(n) =n(n+1)(2n+1)/6,

S³(n) =[S(n)]².

I matematici posteriori usano i termini śreḍhī e paṅkti, che significano entrambi 'fila', per designare in generale le successioni di numeri. Questi termini però non ricorrono nell'Āryabhaṭīya, dove compaiono invece upaciti ('pre-pila') per la serie naturale 1, 2, 3, …, n, citi ('pila') per la somma S(n), citi-ghana ('un solido di pile') per S₂(n), varga-citi-ghana ('un solido di pile quadrate') per S²(n) e ghana-citi-ghana ('solido di pile cubiche') per S³(n).

Le identità algebriche fornite nei due versi seguenti (23-24) sono:

[(a+b)²−(a²+b²)]/2=ab,

{[4ab+(a−b)²]^1/2+(a−b)]}/2=a,

{[4ab+(a−b)²]^1/2−(a−b)]}/2=b.

Queste identità, come pure le formule per le serie, espresse algebricamente, sono pensate in primo luogo per il calcolo, ma possono anche essere interpretate ed espresse per la geometria. I commenti mostrano che questo accadde effettivamente per le serie ed è probabile che sia stato così anche per le identità. In questo senso esse si riferiscono anche a figure oltre che a quantità.

Il cap. 2 dell'Āryabhaṭīya prosegue con un problema puramente numerico concernente l'interesse. Se x è l'interesse sul capitale A per una certa unità di tempo e a è la somma di x e dell'interesse su x per un periodo di tempo t, si ha x+x(x/A)t=a. Āryabhaṭa prescrive (v. 25): x={[Aat+ +(A/2)²]^1/2−(A/2)}/t.

I problemi di proporzioni erano risolti mediante il trairāśika o 'calcolo relativo a tre quantità' (la regola del tre), che è così enunciato: "Quando nel trairāśika si moltiplica il risultato b (phala) [di una certa misura a (pramāṇa)] per una misura scelta c (icchā) e il prodotto è diviso per a, si ha ciò che risulta da c, cioè x (icchā-phala)" (v. 26). Il rapporto fra le quattro quantità è spesso formulato nel modo seguente: "Se da a si ottiene b, che cosa (x) si ottiene da c?". Questa è la 'formulazione verbale' (vācoyukti) di un trairāśika. I dati numerici sono disposti solitamente in riga, a b c, e l'incognita x è determinata in base alla regola suddetta: x=(b×c):a, che compare già, espressa con una terminologia arcaica, nel Jyotiṣavedāṅga (Membro ausiliario del Veda sull'astronomia).

Il calcolo relativo a tre quantità era indispensabile non soltanto per l'astronomia, ma anche per l'economia monetaria. Il primo dei sette esempi per questo tipo di calcolo forniti nel commento di Bhāskara I è il seguente: "Cinque pala di legno di sandalo sono stati da me acquistati per nove rūpaka. Quanto legno di sandalo si può avere per un rūpaka?". Pala e rūpaka sono rispettivamente un'unità di peso e un'unità monetaria.

In relazione alla regola del tre, Āryabhaṭa enuncia regole per l'addizione, la sottrazione, la moltiplicazione e la divisione di frazioni (v. 27).

Per le equazioni lineari del tipo ax+b=cx+d, Āryabhaṭa prescrive: "Si divida la differenza fra i rūpaka b, d di due uomini per la differenza fra le loro gulikā a, c. Il risultato è il prezzo x di una gulikā, se [le loro proprietà] convertite in denaro sono uguali" (v. 30), vale a dire x=(d−b)/(a−c). Gulikā significa 'perlina' o 'pallina', il che fa supporre che all'epoca di Āryabhaṭa, nel procedimento adoperato per la soluzione di equazioni, le quantità incognite fossero indicate da perline o da palline. Un suo contemporaneo, il buddhista Yaśomitra, fa riferimento alle gulikā usate come segnanumeri in un abaco. Un tipico esempio di applicazione di questa regola è fornito da Bhāskara I: "Un primo mercante possiede 7 cavalli sempre dotati di segni propizi e di forza, e vedo anche che in mano ha denaro per 100 [unità]. Un secondo [invece] ha 9 cavalli e denaro per 80 [unità] come suoi beni. Se [si suppone che abbiano] beni uguali, si dica qual è il prezzo di un cavallo, e l'ammontare dei beni uguali" (Āryabhaṭīyabhāṣya, ed. Shukla, 2.30).

Quantità negative erano ammesse almeno per b e d, come dimostra un altro esempio di Bhāskara I: "9 gulikā più un debito (ṛṇa) di 24 rūpaka sono uguali a 2 gulikā e 18 rūpaka. Qual è dunque il prezzo di una gulikā?". In altri termini, si richiede di risolvere l'equazione 9x+(−24)=2x+18. Un'espressione moderna del procedimento di risoluzione è: (9−2)x=18−(−24), da cui 7x=18+24=42 e, infine, x=42/7==6. Per la sottrazione della quantità negativa l'autore cita un verso in pracrito contenente la regola: a−(−b)=a+b.

L'ultima regola (vv. 32-33) fornisce un metodo generale, chiamato kuṭṭaka ('polverizzatore'), per risolvere un sistema indeterminato di equazioni lineari del tipo seguente: "Dividendo un numero intero incognito N successivamente per i numeri interi a₁, a₂,…, a_n, si ottengono rispettivamente i resti r₁, r₂,…, r_n. Qual è il numero N?", ossia N=a_ix_i+r_i, in cui 0≤r_i⟨a_i per i=1, 2,…, n. Āryabhaṭa ricava dapprima x₂ (o x₁) dalle prime due equazioni, x₂=(a₁x₁+c₁)/a₂, dove c₁=r₁−r₂, poi riduce a₁ e a₂ a termini sempre più piccoli (il nome 'polverizzatore' ha origine da questo procedimento) per il tramite di divisioni successive (il cosiddetto 'algoritmo euclideo'), cosicché l'equazione risultante può essere risolta per tentativi; da quella soluzione, seguendo un determinato procedimento, si ottiene una soluzione per l'equazione originaria. Successivamente, calcola il valore di N, poniamo n, con questa soluzione e quindi risolve l'equazione a₁a₂x+n =a₃x₃+r₃, esattamente allo stesso modo. Ripetendo tale procedimento, Āryabhaṭa ottiene il valore di N che soddisfa tutte le equazioni: N=a_ix_i+r_i.

Il kuṭṭaka era usato in astronomia. Per esempio, poniamo che a sia il numero dei giorni di un ciclo yuga e b il numero delle rivoluzioni di un pianeta nello yuga. Se, trascorsi y giorni dall'inizio dello yuga, il pianeta ha compiuto la rivoluzione x volte con un resto pari a r, abbiamo: (by)/a= =x+(r/a), ossia, y=(ax+r)/b. Se, quindi, si conosce r o la longitudine media del pianeta, si ricavano i possibili valori di y e di x mediante il kuṭṭaka. Bhāskara I e altri chiamano questo tipo di kuṭṭaka 'polverizzatore senza resto' (nir-agra-kuṭṭaka), mentre il tipo trattato da Āryabhaṭa è denominato 'polverizzatore con resto' (sa-agra-kuṭṭaka). Quest'ultimo è ricondotto al precedente, come si è visto, nel procedimento di risoluzione.

Āryabhaṭa risolveva così cinque tipi di equazioni: un'equazione lineare a un'incognita (v. 30), un tipo speciale di equazioni lineari simultanee a più incognite (v. 29), un sistema indeterminato di equazioni lineari (vv. 32-33), un'equazione di secondo grado a un'incognita (vv. 20 e 25) e alcuni tipi di forme normali di equazioni di secondo grado (vv. 23-24).

Varāhamihira

Varāhamihira è una delle più insigni personalità nel campo dell'astrologia indiana. La sua attività si svolse ad Avantī (l'odierna Ujjain) nel VI sec. d.C.

Egli suddivideva la 'scienza astrale' (jyotiḥśāstra) in tre rami principali: matematica e astronomia matematica (gaṇita o tantra); astrologia oroscopica (horā); astrologia naturale o divinazione in generale (saṃhitā) (Bṛhatsaṃhitā, Grande raccolta; 1.8-9, 2.2, 2.19). Fu autore di diverse opere di carattere astrologico. Il suo unico testo sul gaṇita, la Pañcasiddhāntikā (Sintesi delle cinque esposizioni conclusive), è un compendio dei testi di cinque scuole astronomiche precedenti. Le sue opere sono importanti anche dal punto di vista della storia della matematica anche se apparentemente non ha scritto nulla di matematica propriamente detta.

Nella Pañcasiddhāntikā la corrispondenza parola-numero (per es., 'occhio'=2, ecc.), basata sul sistema posizionale decimale, compare nella sua forma più evoluta. In questo sistema, una posizione mancante è designata da Varāhamihira con le parole ambara, ākāśa, kha, ecc., tutte aventi il significato di 'cielo' o 'spazio', oppure con la parola bindu 'punto' (quest'ultimo termine indica che nel VI sec. il punto era stato introdotto come simbolo per designare la posizione mancante).

Nella stessa opera compare anche lo zero come numero, cioè come oggetto di operazioni matematiche (addizione, sottrazione, ecc.). Per esempio, Varāhamihira esprime la velocità media quotidiana del Sole in ciascuno dei 12 segni zodiacali a partire dall'Ariete nel modo seguente: "La velocità quotidiana del Sole è, nell'ordine, di 60 [minuti] meno 3, 3, 3, 3, 2, 1, [poi] più 1, 1, 1, 1 e [infine] meno 0, 1 [queste scritture significano, nell'ordine, 60−3 (4 volte), 60−2, 60−1, 60+1 (4 volte), 60−0, 60−1]" (Pañcasiddhāntikā, 3.17).

L'esistenza del simbolo zero sia per le posizioni mancanti nella numerazione posizionale sia nei calcoli eseguiti con questa notazione, diede origine presumibilmente al concetto di zero come numero. Infatti, non è possibile calcolare, per esempio, 15+20=35, senza presupporre la regola per cui 5+0=5. Diverso è il caso dell'abaco, in cui non esiste un simbolo per le posizioni mancanti.

L'autore enuncia esplicitamente il 'procedimento grafico' per costruire una tavola dei seni, secondo un metodo che era stato soltanto accennato da Āryabhaṭa I, e fornisce una tavola dei seni per il raggio R=120 (ibidem, 4.1-15).

Nel capitolo sulla combinazione dei profumi contenuto nella sua opera sulla divinazione, la Bṛhatsaṃhitā (76.22), egli enuncia una regola per calcolare il numero delle combinazioni possibili, _nC_r, di n oggetti presi r a r, e un metodo chiamato 'diffusione per simboli' (loṣṭaka-prastāra) per enumerare correttamente tutte le possibili combinazioni. Nello stesso capitolo fornisce i valori corretti, 84 e 1820, rispettivamente per ₉C₃ e ₁₆C₄, ma afferma erroneamente che il numero dei modi di prendere 4 ingredienti per profumi da un gruppo di 16, tenendo conto delle posizioni 1:2:3:4 (ibidem, 76.13-21), è 4!×4×₁₆C₄=174.720 (essendo 4!=1×2×3×4); il numero esatto è invece quello delle disposizioni di 16 elementi a quattro a quattro, ossia ₁₆P₄=16×15×14×13= 43.680.

Nello stesso capitolo Varāhamihira usa un quadrato magico di ordine quattro per preparare i profumi "buoni per tutti gli scopi". Esso consta delle quattro serie: 2, 3, 5, 8; 5, 8, 2, 3; 4, 1, 7, 6 e 7, 6, 4, 1 (ibidem, 76.23-26). Si tratta del più antico quadrato magico in India: non è regolare perché non è costituito dai numeri da 1 a 16, ma da due serie dei numeri da 1 a 8; tuttavia è 'pan-diagonale', nel senso che non soltanto le due diagonali principali, ma anche tutte le diagonali 'spezzate' hanno come somma la costante magica, in questo caso 18. È presumibile che Varāhamihira abbia prima costruito un quadrato magico con i numeri da 1 a 16 e che successivamente lo abbia modificato, sottraendo 8 dai numeri maggiori di 8 e ottenendo il quadrato non regolare.

La lamina di rame di Sankheda

La lamina di rame di Sankheda contiene la più antica iscrizione conosciuta attestante l'uso della numerazione posizionale decimale. Vi è registrata una concessione fondiaria, con la data espressa sia in parole, sia in cifre: "l'anno trecentoquarantasei 346". I numerali 3, 4 e 6 qui usati sono quelli originariamente usati nella numerazione additiva della scrittura brāhmī. L'era a cui la data fa riferimento è stata identificata con l'era Cedi, che ebbe inizio nel 249 d.C.; l'anno 346 corrisponde dunque al 595-596 d.C.

Tra VII e VIII secolo: la riorganizzazione

Per indicare un indovino (o astrologo), Varāhamihira non usa la parola gaṇaka, bensì i termini tradizionali sāṃvatsara ('colui che si occupa degli anni') o daivacintaka ('colui che riflette sulla volontà divina') o daivajña ('colui che conosce la volontà divina'). Amarasiṃha (attivo fra il V e il VII sec.), invece, nel lessico sanscrito Nāmaliṅgānuśāsana (Insegnamento del genere dei nomi; 2.8.14), elenca il termine gaṇaka nel gruppo delle parole tradizionali. Brahmagupta (628 d.C.) lo usa diverse volte nel Brāhmasphuṭasiddhānta (Siddhānta corretto di Brahmagupta; 13.1, 15.1-17, 18.56-59, 61, 75-87, 91) per designare un esperto di astronomia matematica. La parola ricorre anche nel commento di Bhāskara I (629 d.C.) all'Āryabhaṭīya (Trattato di Āryabhaṭa; esempio 23, 2.32-33) per indicare l'interlocutore in una discussione riguardante un problema astronomico (che comportava un'equazione lineare indeterminata). Dalla prima metà del VII sec. gaṇaka designa dunque un esperto di astronomia matematica o di astrologia oroscopica. Sembra che i gaṇaka usassero una tavola coperta da un sottile strato di polvere (o di sabbia) per eseguire calcoli astronomici, definiti da Brahmagupta (ibidem, 10.62, 66, 67) col termine 'spolvero' (dhūlī-karman).

La parola gaṇaka fu usata in questa nuova accezione anche in testi non matematici; tuttavia ancora nel XII sec. era usata nel significato originario di calcolatore, come testimonia il Mānasollāsa (Il diletto dell'animo), opera sulla politica e altri argomenti attribuita al re Someśvara III (1127-1138) della tarda dinastia Cālukya, in cui il sovrintendente al tesoro reale è chiamato appunto gaṇaka (2.2.95-125).

Il VII sec. vide la riorganizzazione della matematica indiana, con la suddivisione in due campi principali: aritmetica e misurazione, e algebra, in seguito definite rispettivamente pāṭī-gaṇita ('matematica degli algoritmi') o vyakta-gaṇita ('matematica delle quantità note'), e bīja-gaṇita ('matematica dei semi') o avyakta-gaṇita ('matematica delle quantità incognite'). Per 'semi' s'intendono le equazioni algebriche (samīkaraṇa, lett. 'rendere [entrambe le parti] uguali'), che, come i semi delle piante, hanno la potenzialità di generare le soluzioni dei problemi matematici.

Brahmagupta dedicò un capitolo a ciascuno dei due campi nel trattato astronomico Brāhmasphuṭasiddhānta. Il capitolo sull'algebra non è sistematico nell'ordine degli argomenti, come invece saranno testi di algebra più tardi, quali il Bījagaṇita (Matematica dei semi) di Bhāskara II (1150 d.C.). Ciò indica probabilmente che l'algebra, ancora priva di un nome specifico, all'epoca di Brahmagupta era un campo recente nella matematica indiana, anche se l'uso di equazioni per la risoluzione di problemi matematici aveva già una lunga storia e non mancavano opere sulle equazioni, come attesta Bhāskara I, contemporaneo di Brahmagupta.

Brahmagupta

Brahmagupta, figlio di Jiṣṇu, a quanto egli stesso afferma, scrisse il trattato di astronomia Brāhmasphuṭasiddhānta, in 25 capitoli, all'età di trent'anni, nell'anno 550 dell'era Śaka (corrispondente al 628 d.C.). Era nato dunque nel 598, e risulta ancora attivo all'età di 67 anni, nel 665, quando compose un'altra opera sull'astronomia, il Khaṇḍakhādyaka (Bocconcini). Il commentatore Pṛthūdakasvāmin (attivo nell'864) lo chiama 'il maestro di Bhillamāla', città capitale della dinastia Cāpa all'epoca del re Vyāghramukha e identificata con l'odierna Bhinmal, città del Rajasthan presso il monte Abu, vicino al confine con il Gujarat.

Nel Brāhmasphuṭasiddhānta cinque sono i capitoli dedicati in modo particolare alla matematica. Il cap. 12, intitolato semplicemente Gaṇita, il termine all'epoca più comune per designare la matematica, verte su aritmetica e misurazione; il cap. 18, dedicato all'algebra, era intitolato Kuṭṭaka (Polverizzatore), con riferimento al primo argomento trattato, cioè le equazioni lineari indeterminate. Questi due capitoli costituiscono l'insieme delle conoscenze matematiche indiane del tempo. Il cap. 19, Conoscenze relative allo gnomone e all'ombra, tratta delle misurazioni delle ombre e delle luci e può essere considerato un supplemento alla sezione sulla matematica applicata delle ombre nel cap. 12. Sappiamo che il cap. 20, Estensione (o Supplemento) all'accatastamento dei metri, si occupa della combinatoria della prosodia, argomento trattato anche dagli studiosi di metrica a cominciare da Piṅgala, ma non è stato ancora decifrato. Nel cap. 21, Astronomia sferica, c'è una piccola sezione (vv. 17-23) chiamata Jyāutpatti (Produzione di seni) che tratta di trigonometria, argomento che nell'Āryabhaṭīya fa parte del capitolo sulla matematica.

Brahmagupta introduce così gli argomenti che tratterà nel cap. 12: "Colui che conosce bene ciascuna delle venti operazioni fondamentali (parikarman), a cominciare dall'addizione, e delle otto matematiche per usi pratici (vyavahāra), l'ultima delle quali si occupa delle ombre, è un matematico (gaṇaka)" (v. 1). Le venti operazioni fondamentali sono: otto calcoli aritmetici (addizione, sottrazione, moltiplicazione, divisione, elevazione al quadrato, estrazione della radice quadrata, elevazione al cubo ed estrazione della radice cubica) relativi sia a numeri interi sia a frazioni, cinque classi (jāti) di riduzioni di frazioni a denominatore comune e sette tipi di calcoli basati sulle proporzioni (regole del tre, del cinque, del sette, del nove e dell'undici, regola inversa del tre e permuta). Gli otto tipi di matematica per usi pratici sono: composti (miśraka: un composto è, per es., la somma del capitale investito e dell'interesse), serie (śreḍhī), figure piane (kṣetra), scavi (khāta), pile di mattoni (citi), taglio di tronchi (krākacika), mucchi di granaglie (rāśi) e ombre (chāyā).

Le regole di Brahmagupta per i primi sei calcoli aritmetici riguardano soltanto le frazioni, forse perché si pensava che quelle per i numeri interi fossero troppo elementari per il lettore. L'autore aggiunge tuttavia un breve supplemento alla fine del capitolo sulla moltiplicazione e divisione dei numeri interi e dà numerose regole aggiuntive per le frazioni, tra cui una formula per il quadrato di un numero accompagnato da una frazione sessagesimale: [a+(b/60)]²≈a²+(ab/30), come dire che si trascura rispetto agli altri il termine b²/3600.

La sezione sulla 'matematica per usi pratici delle figure piane' può essere suddivisa in quattro sottosezioni: misure di triangoli e quadrilateri, loro costruzione, un problema che coinvolge due asceti, e misure di un cerchio.

Brahmagupta consegue risultati notevoli su alcune proprietà dei quadrilateri. A lui si deve una formula che estende all'area di un quadrilatero inscritto in un cerchio la formula di Erone per l'area di un triangolo: A=[(s−a)(s−b)(s−c)(s−d)]^1/2, dove a, b, c, d sono le lunghezze dei quattro lati e s è la loro semisomma. La regola per il calcolo delle due diagonali e₁ ed e₂ è: e₁= [(ad+bc):(ab+cd)×(ac+bd)]^1/2, e₂=[(ab+cd): (ad+bc)×(ac+bd)]^1/2. Egli indica anche un metodo per costruire un quadrilatero inscrivibile in un cerchio, i cui lati e le cui diagonali sono razionali o interi, e le cui diagonali sono ortogonali: se a₁, b₁, c₁ e a₂, b₂, c₂ sono i tre lati (razionali o interi) di due triangoli rettangoli (di ipotenuse c₁ e c₂), i quattro lati del quadrilatero in questione saranno c₂a₁, c₂b₁, c₁a₂, c₁b₂. Nelle formule per la circonferenza e per l'area di un cerchio il rapporto π prende il valore 3 per fini pratici e 10^1/2 per calcoli accurati.

Nelle quattro sezioni successive sono trattati i solidi. Le formule per il volume di una piramide, di un tronco di piramide e di un cono sono corrette, ma non lo sono quelle per il volume e per la superficie di una sfera.

Nel primo verso del cap. 18 Brahmagupta sottolinea l'importanza del metodo del polverizzatore: "Poiché è quasi impossibile comprendere i quesiti [posti da altri] senza il polverizzatore, ne parlerò rispondendo a tali quesiti". Oltre al polverizzatore, in questo capitolo Brahmagupta si occupa di diversi argomenti riguardanti le equazioni algebriche; nell'ordine: (1) polverizzatore (kuṭṭaka, inclusi il polverizzatore con resto e il polverizzatore costante senza resto, vv. 3-29); (2) numeri positivi (dhana) e negativi (ṛṇa) e zero (kha) (vv. 30-35); (3) due serie di forme normali algebriche (v. 36); (4) numeri irrazionali (karaṇī, vv. 37-40); (5) numeri incogniti (avyakta, vv. 41-42); (6) equazioni lineari a un colore, cioè equazioni lineari a un'incognita (ekavarṇa-samīkaraṇa, v. 43); (7) eliminazione del termine medio [di un'equazione di secondo grado a un'incognita] (madhyaharaṇa, vv. 43-50); (8) equazioni a più colori, cioè a più incognite (anekavarṇa-samīkaraṇa, vv. 51-59); (9) equazioni con un prodotto (bhāvitaka, axy=bx+cy+d, vv. 60-63); (10) equazione 'natura del quadrato' (vargaprakṛti, vv. 64-95), ossia l'equazione indeterminata di secondo grado Px²+t=y² (v. cap. IX, par. 2, per i rapporti fra gli Śulbasūtra e la matematica posteriore); (11) quattro serie di forme normali (due delle quali identiche a quelle del punto 3, vv. 96-99). Brahmagupta afferma che la padronanza di questi argomenti rende "maestro tra gli esperti della dottrina [astronomica] (tantra)" (v. 2).

Brahmagupta descrive sistematicamente la regola dei segni per le sei operazioni aritmetiche tra numeri positivi e negativi e lo zero. Le regole per lo zero, espresse in notazione moderna, sono: a+(−a)=0, a±0=a, 0±0=0, a×0=0×a=0, 0×0=0, 0:a=0, a:0=a/0, 0:0=0, 0²=0, 0^1/2=0. Brahmagupta definisce la frazione a/0 'zero-denominatore' (kha-hara), vale a dire 'quella il cui denominatore è zero', ma non ne specifica il valore.

Nella numerazione posizionale i calcoli possono far intervenire operazioni con lo zero, escluse la divisione e la radice quadrata. Le regole per queste ultime sembra siano state motivate dalle equazioni lineari e quadratiche. Nella risoluzione dell'equazione ax+b=cx+d, le regole per la divisione 'per zero' e 'di zero' diventano necessarie quando a=c e b=d rispettivamente; nella risoluzione di ax²+bx=c, secondo l'algoritmo fornito da Brahmagupta e altri, si rende necessaria una regola per la radice quadrata di 0 quando b²+4ac=0.

Brahmagupta fornisce regole di calcolo anche per le sei operazioni aritmetiche con i numeri irrazionali. Queste regole non sono date direttamente per K^1/2 ma per K, denominato karaṇī. Per esempio, la regola per l'addizione (⊕) di due karaṇī, K₁ e K₂, è la seguente: quando il prodotto, K₁K₂, è un quadrato, K₁⊕K₂=[(K₁/a)^1/2+(K₂/a)^1/2]²×a, dove a è qualsiasi numero che renda K₁/a e K₂/a quadrati. La regola per la divisione delle karaṇī è basata sulla razionalizzazione del divisore e quella per la radice quadrata sulla relazione [R+K^1/2]^1/2=[(R+m)/2]^1/2+[(R−m)/2]^1/2, in cui m è un numero intero tale che R²−K=m² .

Nella prima metà del VII sec. gli Indiani avevano a disposizione numeri sia razionali sia irrazionali, ed erano in grado di eseguire con essi le sei operazioni aritmetiche. Ciò favorì senza dubbio lo sviluppo dell'algebra in India.

Il termine comunemente usato dagli autori successivi per incognita è avyakta ('immanifesto' o 'ignoto'). Ricorre spesso anche il termine varṇa ('colore'), soprattutto quando il problema comporta più incognite (ma nel trattato non s'incontrano nomi di colori per designarle). Non sappiamo perché si usasse il termine colore, anche se forse è da connettere con la gulikā ('perlina') di Āryabhaṭa. Sembra che Brahmagupta scrivesse i due membri di un'equazione ponendoli uno sopra l'altro (per un'equazione di secondo grado), come faceva anche Bhāskara I, suo contemporaneo, ma sul modo che egli aveva di esprimere le equazioni non abbiamo altre notizie.

Bisogna notare che in quest'opera non compare la parola yāvattāvat ('tanto quanto'), menzionata da Bhāskara I a proposito della gulikā di Āryabhaṭa e che nell'algebra indiana posteriore sarebbe diventata il termine più comune per indicare le incognite. Ciò fa supporre che yāvattāvat appartenesse in origine a una tradizione diversa da quella delle 'perline' e dei 'colori' (forse a quella jaina, dato che il termine è attestato nell'elenco dei dieci argomenti di matematica riportato in un testo canonico jaina).

Il risultato più notevole conseguito da Brahmagupta in algebra è un teorema sull'equazione 'natura del quadrato', ora noto come 'lemma di Brahmagupta'. Nella notazione odierna esso è espresso nel modo seguente: se (x, y, t)=(a₁, b₁, c₁) e (x, y, t)=(a₂, b₂, c₂) sono due terne di soluzione dell'equazione Px²+t=y² (denominata da Brahmagupta appunto 'natura del quadrato'), anche (a₁b₂+a₂b₁, Pa₁a₂+b₁b₂, c₁c₂) è una soluzione della stessa equazione. Brahmagupta dimostra anche che, quando l'equazione è stata risolta per t=−1 o ±2 o ±4, può essere risolta anche per t=1 con l'applicazione del medesimo lemma. Lo studio dell'equazione 'natura del quadrato' fu probabilmente dettato dal problema di trovare la diagonale di un quadrato, trattato negli Śulbasūtra (Aforismi sulla costruzione di altari; v. cap. IX, par. 2).

Nella sezione sulla trigonometria del cap. 21 Brahmagupta prescrive un metodo per la costruzione di una tavola di seni, chiamato 'produzione dei seni', che corrisponde al 'procedimento grafico' di Bhāskara I. Il testo presenta due tavole di seni; in esse sono tabulati i valori di J_i=Rsen(αi) per i=1, 2, 3,…, n rispettivamente per R=3270 e n=24 (cap. 2) e per R=150 e n=6 (cap. 25). Dopo la seconda tavola sono date due formule d'interpolazione per trovare valori approssimati di seni non inclusi nelle tavole. Una consiste in un'interpolazione lineare, Rsen(αi+θ)≈J_i+(θ/α) ×K_i+1, con 0⟨θ⟨α, mentre l'altra è equivalente alla formula di Newton-Stirling troncata alle differenze del secondo ordine, Rsen(αi+θ)≈J_i+(θ/α)×[(K_i+K_i+1)/2]−(θ/α)²×[(K_i−K_i+1)/2] (ricordiamo che K_i=Rsen(αi)−Rsen[α(i−1)]).

Bhāskara I

Bhāskara I, attivo nella prima metà del VII sec. nel Saurāṣṭra, forse a Valabhī, presso l'odierna Bhāvnagar, compose tre opere che esponevano gli insegnamenti di Āryabhaṭa I, "basandosi sulla continuità della tradizione". In ordine cronologico esse sono: il Karmanibandha (Trattato sul calcolo [astronomico]), noto anche come Mahābhāskarīya (Trattato esteso di Bhāskara); un commento in prosa all'Āryabhaṭīya scritto nell'anno 551 dell'era Śaka (629 d.C.); infine, una versione abbreviata della prima opera, anch'essa intitolata Karmanibhanda o Laghubhāskarīya (Trattato conciso di Bhāskara). Di particolare importanza per la storia della matematica indiana è la seconda, cioè il commento all'Āryabhaṭīya, da cui si ricavano informazioni preziose su alcuni aspetti della matematica indiana del VII secolo.

Qui ogni verso del cap. 2 dell'Āryabhaṭīya, dedicato alla matematica, è commentato con una parafrasi, con la spiegazione dei termini tecnici, l'elenco dei relativi sinonimi, risposte a interrogativi e a obiezioni, e infine con esempi, per lo più in versi, di problemi da risolvere mediante l'applicazione della regola esposta nel verso. Dopo ciascun esempio l'autore fornisce un elenco o una tabella (denominati nyāsa o sthāpanā) dei dati numerici dell'esempio, un calcolo (karaṇa) che risolve il problema, e talvolta una verifica (pratyayakaraṇa) della soluzione. In epoca successiva la verifica fu trascurata, ma ai tempi di Bhāskara la si considerava molto importante. Dai calcoli relativi agli esempi si possono desumere alcune informazioni sui procedimenti e le espressioni matematiche del tempo.

Una posizione mancante (kha) nella numerazione posizionale decimale era indicata da un cerchietto ('o'), detto bindu (lett. 'punto'), che era posto anche in alto a destra di un numero negativo. Una frazione era espressa con il numeratore sopra il denominatore (come si fa oggi) ma senza barra divisoria e la parte frazionaria di un numero era posta sotto la sua parte intera. Così, per esempio, il diametro del cerchio di riferimento della tavola dei seni di Āryabhaṭa I, la cui circonferenza è 21.600, è

poiché il valore che Āryabhaṭa I prende per π è 62.832/20.000, mentre la circonferenza della Terra, il cui diametro, sempre secondo Āryabhaṭa I, è di 1050 yojana (11.760 km ca.), vale

Bhāskara I chiamava un numero irrazionale K^1/2 'karaṇī K'. Per esempio, calcolando il volume di una sfera di diametro 2 secondo la formula (errata) di Āryabhaṭa I esprime il risultato come:

,

che equivale a

Egli, inoltre, esprimeva l'equazione ax+b=cx+d come

a b

c d

e ciò significa che probabilmente non conosceva ancora l'uso delle abbreviazioni yā per yāvattāvat e rū per rūpaka, pur conoscendo le parole in questione. Commentando il termine gulikā ('perlina') usato da Āryabhaṭa, Bhāskara I dice: "Queste stesse gulikā, i cui valori non sono noti, sono dette yāvattāvat, mentre i rūpaka (unità di moneta) sono gli stessi anche in questo caso" (Āryabhaṭīyabhāṣya, ed. Shukla, 2.30). In epoche successive, la suddetta equazione di primo grado sarebbe stata espressa come

yā a   rū  b

yā c rū d.

Bhāskara I chiama le equazioni algebriche 'semi' (bīja) e ne enumera quattro tipi; da questi hanno origine gli otto tipi di matematica 'degli affari materiali' o 'per usi pratici' (vyavahāra-gaṇita). Dopo aver spiegato brevemente ognuno degli argomenti di cui si occupa la 'matematica per usi pratici', osserva:

Per questa matematica per usi pratici dagli otto nomi vi sono 4 semi [detti] primo, secondo, terzo e quarto, [o altrimenti detti] yāvattāvat, vargāvarga [equazioni quadratiche?], ghanāghana [equazioni cubiche?] e viṣama [equazioni a più incognite?]. Per ciascuno di questi [argomenti] dai maestri, a partire da Maskari, Pūraṇa e Mudgala, è stato composto un libro di regole ed esempi. Come può dunque questo maestro [Āryabhaṭa] esporre tutto ciò nel presente libretto? (ibidem, 1.1)

Le opere di Maskari e degli altri di cui parla, sembrano irrimediabilmente perdute.

Nel commento all'Āryabhaṭīya, inoltre, Bhāskara I spiega in dettaglio il polverizzatore, sia con resto sia senza, e le sue applicazioni in astronomia, fornendo numerosi esempi. Anche nel Mahābhāskarīya espone lo stesso argomento. Quanto alla geometria, è probabile che conoscesse una dimostrazione del teorema di Pitagora.

Il termine sanscrito che più si avvicina a dimostrazione è upapatti. Bhāskara I lo usa in diversi casi. Per esempio, nel confutare la formula jaina per la circonferenza di un cerchio di diametro d, c =(10d²)^1/2, afferma che "per questo vi è soltanto una tradizione (āgama), ma nessuna upapatti"; dimostra poi l'erroneità delle formule per l'area di un settore circolare, B=10^1/2ah/4, e per l'arco di questo, b=10^1/2[(a/4)+(h/2)], dove a e h rappresentano rispettivamente la corda e la freccia (o l'altezza); queste due formule sono basate sul valore di 10^1/2(=3,16227…) attribuito dai jaina al rapporto π tra la circonferenza e il diametro di un cerchio. Nel Mahābhāskarīya egli dà un'approssimazione razionale molto accurata del seno di un angolo θ, ossia: Rsenθ≈4Rθ (180−θ) /{40.500+ −[θ(180−θ)]}.

Kaṭapayādi, la notazione alfabetica dei numeri

Brahmagupta e Bhāskara I usavano i numerali ordinari e le parole/numero basate sull'associazione tra cose e numeri. Intorno alla stessa epoca anche nell'India meridionale si cominciò a usare una notazione alfabetica detta kaṭapayādi (lett. 'quella che comincia per k, ṭ, p e y'). Essa è usata nel Candravākya (Proposizioni sulla Luna) del leggendario astronomo Vararuci, vissuto, secondo la tradizione, nel IV sec. d.C. L'opera più antica in cui compare questa notazione sembra però essere il Grahacāranibandhana (Compilazione sul corso dei pianeti) di Haridatta (683 d.C.). La kaṭapayādi divenne molto popolare nella letteratura matematica (soprattutto in astronomia) e in altri campi come l'epigrafia e la musica.

In questa notazione, basata sulla numerazione posizionale decimale, ciascuna sillaba di una parola (o di una successione di sillabe) corrisponde a una posizione decimale; soltanto la prima consonante di una sillaba e l'eventuale vocale iniziale hanno valori numerici. Essa consente di realizzare con facilità successioni di sillabe che hanno un significato ordinario e al tempo stesso un valore numerico. Così, a-na-nta-pu-ra significa sia 'Città dell'Infinito (o di Viṣṇu)' sia 2(r)1(p)6(t)0(n)0(a)≡21.600. La notazione kaṭapayādi ha diverse varianti, di cui la più significativa è quella di Āryabhaṭa II, che assegna a ogni consonante una posizione decimale in ordine ascendente.

Il Manoscritto di Bakhshālī

Il Manoscritto di Bakhshālī è il più antico manoscritto esistente della matematica indiana. È stato riportato alla luce in cattive condizioni a Bakhshālī, presso Peshawar (oggi in Pakistan), nel 1881 ed è attualmente conservato nella Bodleian Library dell'Università di Oxford. La parte superstite consta di 70 fogli frammentari. È scritto su corteccia di betulla nel più antico tipo di scrittura śāradā, usata nell'India nordoccidentale fra l'VIII e il XII secolo. La lingua è un sanscrito ampiamente influenzato dai dialetti di quelle regioni.

L'opera consiste in una disordinata raccolta di regole matematiche e di esempi tratti da vari testi; è in versi e gli esempi sono svolti in commenti in prosa. Spesso è data la verifica delle soluzioni.

Nel colophon della sezione sulla regola del tre si legge: "Questo è stato scritto da Chajakaputra (figlio di Chajaka), brahmano e re dei matematici, per Hasika, figlio di Vasiṣṭha, affinché possa essere usato [anche] dai suoi discendenti". Ciò lascia supporre che il compilatore-commentatore dell'opera (o almeno di una sua parte) fosse il figlio di Chajaka. Poco distante compare il frammento di una parola ‒rtikāvati, che dovrebbe indicare la regione di Mārtikāvata, probabile luogo di composizione.

Le datazioni sinora proposte per il testo di Bakhshālī oscillano fra il III e il XII sec., ma un recente studio comparativo ha messo in luce numerose affinità con il commento di Bhāskara I all'Āryabhaṭīya, soprattutto per lo stile espositivo e la terminologia. Si può dunque ipotizzare che entrambe le opere risalgano più o meno allo stesso periodo, anche se non è da escludere che alcune regole ed esempi del Manoscritto di Bakhshālī siano di epoca precedente.

Le regole menzionate nella parte superstite del manoscritto sono: (1) operazioni aritmetiche (l'addizione, ecc.), inclusa la formula di approssimazione della radice quadrata (a²+r)^1/2≈a+[r/(2a)]−[(r/(2a)]²/{2[a+r/(2a)]} (sulle origini di questa formula, v. cap. IX, par. 2); (2) regole generali applicabili a diversi tipi di problemi, come la regola del tre, la regula falsi, ecc.; (3) regole per problemi puramente numerici, come equazioni algebriche e progressioni aritmetiche; (4) regole per questioni relative al denaro, come comprare e vendere, ecc.; (5) regole per i problemi dei viaggiatori, come equazioni riguardanti i viaggi, ecc.; (6) regole per problemi geometrici, come il calcolo del volume di solidi irregolari. Le regole del primo tipo compaiono soltanto come citazioni nei 'calcoli' degli esempi, la maggior parte delle altre vi figura autonomamente e potrebbe appartenere al capitolo 'composti' (un composto è, per es., la somma del capitale investito e dell'interesse) o a quello 'serie matematiche' di un libro sulle pāṭī ('algoritmi'). Queste regole non sono però organizzate secondo la classificazione abituale degli otto tipi di matematica applicata; il criterio scelto dal compilatore non è chiaro.

Il Manoscritto di Bakhshālī usa la numerazione posizionale decimale, con un punto per indicare lo zero. Per le operazioni matematiche si usano spesso abbreviazioni di parole; per esempio, yu sta per yuta ('aumentato'), gu per guṇa o guṇita ('moltiplicato'), e così via. Per la sottrazione si usa il segno +, che era in origine la lettera iniziale della parola ṛṇa ('debito') nelle scritture in uso nel periodo delle dinastie Kuṣāṇa e Gupta, tra il II e il VI sec., sopravvissuto soltanto come simbolo per la sottrazione (o per una quantità negativa) nella scrittura śāradā e in altri alfabeti dell'India settentrionale.

Il simbolo yā per l'incognita compare una volta ed è usato non in un'equazione algebrica, ma in un esempio pratico per ridurre i dati a una forma in cui si possa applicare meccanicamente una certa regola. Questo uso limitato del simbolo sembra confermare l'ipotesi qui avanzata riguardo alla datazione di quest'opera, ossia che essa appartenga all'incirca alla stessa epoca in cui era attivo Bhāskara I, che non faceva uso del simbolo in questione.

Vīrasena

Nel 781 d.C., Vīrasena, uno studioso della setta jaina dei Digambara, compose un commento in pracrito intitolato Dhavalā (La bianca) al Chakkhaṇḍāgama (Dottrina in sei sezioni) di Puṣpadanta e Bhūtabali, nel quale usa numerose formule geometriche. Egli calcola, per esempio, il volume dello 'spazio del mondo' (loka-ākāśa) usando, allo scopo di confutarlo, il procedimento della setta Śvetāmbara; dimostra infatti che così si trova un volume di soli 164 e 28/113 rajju cubici, mentre dovrebbe essere di un loka cubico, cioè 7³=343 rajju cubici (7 rajju=1 loka).

Come si è detto, la setta Śvetāmbara sostiene che lo 'spazio del mondo' consiste in tre tronchi di cono sovrapposti, dei quali i due superiori hanno le stesse dimensioni. Vīrasena calcola il volume di ciascun tronco di cono non ricorrendo a una formula, bensì scomponendolo. Elimina innanzitutto il cilindro centrale, trasformando la porzione rimanente in un pentaedro che chiama 'cesto per spulatura', lasciandone intatto il volume. Poi scompone il pentaedro in un prisma triangolare e in un numero infinito di parallelepipedi rettangolari, i cui volumi formano una progressione geometrica di ragione 1/4.

Nel calcolare il volume del cilindro centrale l'autore cita un verso sanscrito che prescrive la formula c=3d+(16d+16)/113 per la circonferenza di un cerchio di diametro d. Questa strana formula era ottenuta, con ogni probabilità, come approssimazione della formula di Āryabhaṭa I, c=(62.832/20.000)d, nella quale il rapporto indicato approssimava π. L'ideatore della formula deve aver innanzitutto ottenuto 355/113 quale terzo convergente della frazione continua per 62.832/20.000, e quindi aggiunto 16/113 al membro destro dell'uguaglianza provvisoria c=(355/113)d, come correzione necessaria affinché c assuma il valore 62.832 quando d=20.000, come nel caso della formula di Āryabhaṭa I.

Per la somma della progressione geometrica infinita, la formula che egli usa è sostanzialmente S=a+(a/p)+(a/p²)+…= =ap/(p−1), in cui p>1, anche se non è detto esplicitamente.

Śrīdhara

Śrīdhara fu attivo in un'epoca imprecisata tra Brahmagupta (628), del quale critica una delle formule geometriche, e Govindasvāmin (800 ca.-850 ca.), che cita la formula di Śrīdhara per la somma delle successioni di numeri naturali. Śrīdhara è uno dei primi autori a scrivere trattati separati per ciascuno dei due campi principali della matematica, ossia la matematica degli algoritmi (pāṭī-gaṇita) e quella dei 'semi' (ossia delle equazioni, bīja-gaṇita). Di lui si conservano il Pāṭīgaṇita (Matematica degli algoritmi), la Triśatikā ([Libro in] trecento versi) o Gaṇitasāra (Essenza della matematica) e la Gaṇitapañcaviṃśī (Matematica in venticinque versi), appartenenti tutti alla matematica degli algoritmi. È certo che egli dedicò almeno un'opera alla matematica dei 'semi' (equazioni), della quale Bhāskara II cita parte di una regola per un'equazione di secondo grado a un'incognita nel Bījagaṇita (Matematica dei semi, 1150 d.C.).

Anziché le 10 posizioni decimali di Āryabhaṭa I, Śrīdhara adottò le 18 posizioni in cui il niyuta vedico per 10⁵ è sostituito dal lakṣa non vedico, mentre per le ultime quattro posizioni (da 10¹⁴ a 10¹⁷) sono ripristinati i nomi vedici (da 10⁹ a 10¹²). Questi nomi, con trascurabili differenze dovute all'uso di sinonimi, furono adottati dalla gran parte dei matematici hindu.

Il Pāṭīgaṇita inizia con un indice dei contenuti e, dopo le 18 posizioni decimali e le tavole dei pesi e delle misure, tratta le 29 operazioni di base e i 9 tipi di matematica pratica. Dall'indice sappiamo quali argomenti trattasse la parte perduta. Le 29 operazioni di base comprendono gli 8 calcoli aritmetici per i numeri interi e altrettanti per le frazioni, 6 riduzioni di frazioni a un comune denominatore e 7 calcoli basati sulle proporzioni. I 9 tipi di matematica applicata sono gli 8 argomenti abituali, che cominciano con 'composti', più uno nuovo, chiamato 'verità dello zero'.

La parte a noi pervenuta del capitolo sulla matematica per usi pratici contiene molti argomenti nuovi. Nella sezione sulle 'successioni' sono presentate per la prima volta regole per le progressioni geometriche e per l'espressione geometrica di una progressione aritmetica (per mezzo di un trapezio). Come il Manoscritto di Bakhshālī, anche Śrīdhara ammette le frazioni come ragioni di progressioni aritmetiche.

Nella Triśatikā, Śrīdhara usa 10^1/2 per π e fornisce per la prima volta in India le formule corrette per il volume della sfera, V=(d³/2)+[(d³/2)/18], dove è usata l'approssimazione razionale 19/6 per 10^1/2, ossia (3²+1)^1/2≈3+1/(2×3), e per il volume del tronco di cono, V={h{10[d₁²+d₂²+(d₁+d₂)²]²}^1/2}/24, dove h è l'altezza e d₁ e d₂ sono i diametri dei cerchi di base. Si è ipotizzato che Śrīdhara usasse 22/7 per π.

Virahāṅka

Virahāṅka, vissuto in un'epoca non precisata tra il VI e l'VIII sec., è l'autore di un trattato di prosodia, dal titolo Vṛttajātisamuccaya (Raccolta di metri vṛtta e jāti). Il vṛtta è un verso il cui metro è regolato dal numero e dalla posizione delle sillabe in ciascun quarto della stanza, mentre la jāti è un verso il cui metro è regolato dal numero di more (mātrā) e dalla posizione delle sillabe in ciascun quarto. La lunghezza di una sillaba può essere di una mora (breve) oppure di due more (lunga).

Ovviamente esiste una sola successione di una mora, cioè una sola sillaba breve. Successioni di due more si possono ottenere con una sillaba lunga oppure con due sillabe brevi. Le sequenze di n more (n>2) si ottengono tutte, ciascuna una volta sola, aggiungendo o una sillaba lunga alle successioni di n−2 more o una sillaba breve alle successioni di n−1 more. Se a_n è il numero delle successioni di n more, allora si ha la relazione a_n=a_n−2+a_n−1, con a₁=1, a₂=2, che dà luogo a una successione di Fibonacci, chiaramente riconosciuta ed esplicitamente formulata da Virahāṅka (Vṛttajātisamuccaya, 6.49) oltre 400 anni prima del matematico pisano.

Dal IX al XIV secolo: gli sviluppi successivi

Govindasvāmin

Seguace della scuola di matematica e astronomia di Āryabhaṭa I, Govindasvāmin fu attivo nella prima metà del IX sec. in Kerala. Si sono conservati i suoi commenti al Mahābhāskarīya (Trattato esteso di Bhāskara) di Bhāskara I e alla seconda metà dello Horāśāstra (Trattato sull'astrologia) di Parāśara (databile tra il 600 e il 750); tre sue opere sull'astronomia, sull'astrologia e la matematica sono invece note soltanto da riferimenti e citazioni.

Nel commento (1540 ca.) alla Līlāvatī (La giocosa) di Bhāskara II, Śaṅkara Vāriyar cita numerose regole di Govinda sui calcoli aritmetici con numeri interi e razionali senza specificare da quali testi siano state tratte. È probabile che la maggior parte di queste regole provenisse dal Gaṇitamukha (Introduzione alla matematica), la sua opera sulla matematica che non ci è pervenuta.

Govindasvāmin dimostra un profondo interesse per i fondamenti logici della regola del tre. Nel commento al Mahābhāskarīya (1.7) fornisce una definizione, con una spiegazione dettagliata, dei quattro termini (pramāṇa, pramāṇa-phala, icchā e icchā-phala) della regola del tre e, in tre versi citati da Śaṅkara, confronta questi quattro termini con i costituenti dell'inferenza (anumāna) così come descritta dai logici indiani. Secondo questa scuola filosofica, il modello d'inferenza è: "Su quella montagna c'è fuoco perché c'è fumo. Dove c'è fumo c'è fuoco, come in cucina". Secondo Govindasvāmin i quattro termini della regola del tre corrispondono nell'ordine al fumo e al fuoco nella cucina, e agli stessi nella montagna. La regola del tre può quindi essere considerata un'inferenza.

Mahāvīra

Mahāvīra, matematico jaina della setta Digambara, fu attivo in Karnataka durante il regno di Amoghavarṣa (814 ca.-880 ca.), al quale rende omaggio all'inizio dell'unica sua opera a noi pervenuta, il Gaṇitasārasaṃgraha (Compendio dell'essenza della matematica).

Il Gaṇitasārasaṃgraha è un trattato sulle pāṭī ('algoritmi'), però organizzato diversamente da altre opere di questo genere. Il libro è voluminoso (consta di oltre 1130 versi contenenti regole ed esempi) ed è suddiviso in nove capitoli, il primo dedicato alla terminologia, gli altri otto ai cosiddetti vyavahāra, termine che sembra avere qui il significato non di 'matematica per usi pratici', bensì di 'procedimento matematico' o 'algoritmo', in quanto comprende tutti gli argomenti dell'opera, incluse le operazioni fondamentali (parikarman).

Il cap. 1, Terminologia, contiene un elogio della matematica, pesi e misure, regole per lo zero e i numeri negativi, la notazione parola/numero, i nomi delle posizioni decimali e gli otto meriti di un calcolatore. Mahāvīra afferma qui esplicitamente che una quantità negativa non ha una radice quadrata poiché non è un quadrato.

Il cap. 2, Procedimenti per le operazioni di base, fornisce le regole per gli otto tipi ordinari di calcoli aritmetici con i numeri interi, tranne l'addizione e la sottrazione, mentre sono enunciate quelle per la somma e la differenza di progressioni aritmetiche e geometriche.

Nel cap. 3, Procedimenti per la riduzione di frazioni a denominatore comune, sono trattate le suddette otto operazioni in riferimento alle frazioni e particolarmente interessante risulta la scomposizione delle frazioni. Una delle regole di Mahāvīra a questo riguardo è, in notazione moderna, (q/p)=(1/r)+[s/(rp)], dove r e s sono numeri interi che soddisfano la condizione p+s=qr.

Il cap. 4, Procedimenti per problemi vari, verte sulle diverse classi (jāti) di problemi che si traducono in un'equazione di primo o secondo grado a un'incognita. Per esempio, uno dei problemi della classe 'prodotto parziale' può essere espresso, modernamente, come x−[(b/a)x][(d/c)x]=e, di cui Mahāvīra fornisce la soluzione x={ac/(bd)±{[ac/(bd)−4e]ac/(bd)}^1/2}/2. Sembra che Mahāvīra sia stato il primo in India ad ammettere due soluzioni per un'equazione di secondo grado. Śrīdhara si occupa di analoghi problemi di 'classi' nella sezione sui 'composti' del Pāṭīgaṇita (Matematica degli algoritmi).

Il cap. 5, Procedimenti sulla regola del tre, è dedicato alle regole del tre, del cinque, del sette e del nove, alla regola inversa del tre e alla vendita di creature viventi. Questi argomenti sono di solito inclusi tra le 'operazioni fondamentali'.

Il cap. 6, Procedimenti sui composti, verte sull'interesse, la distribuzione proporzionale, i temi detti kuṭṭīkāra ('frazionamento' o 'analisi'), le successioni di numeri e il calcolo combinatorio applicato alla prosodia sanscrita. I kuṭṭīkāra risolvono diversi tipi di equazioni determinate e indeterminate di primo e secondo grado, e comprendono inoltre due metodi relativi al polverizzatore, cioè per la determinazione di soluzioni dell'equazione y=(ax+c)/b in numeri interi. In uno di essi Mahāvīra, come Āryabhaṭa I e Brahmagupta, arresta l'algoritmo euclideo per la determinazione del massimo comun divisore fra a e b (supposti relativamente primi) in un punto a partire dal quale si possono facilmente trovare soluzioni per tentativi; nell'altro lo porta avanti fino a ottenere come resto l'unità. In quest'ultimo caso sono eliminati i tentativi dal metodo del polverizzatore, che si riduce così a un algoritmo perfettamente meccanico. Mahāvīra fornisce anche diversi esempi numerici del 'polverizzatore con resto', vale a dire del problema di trovare un intero N che diviso per due interi a e b dia per resto rispettivamente c₁ e c₂, ossia N=ax+c₁=by+c₂.

Il cap. 7, Procedimenti per il calcolo geometrico, presenta una classificazione di figure piane, calcoli pratici (vyāvahārika) di triangoli, quadrilateri e cerchi (con π=3), calcoli accurati (sūkṣma) degli stessi (con π=10^1/2), 'procedimenti per generare' (janya-vyavahāra) triangoli e quadrilateri razionali a partire da determinati numeri chiamati 'semi' (bīja) mediante terne pitagoriche, e 'procedimenti demoniaci' (paiśācika-vyavahāra). Questi ultimi comprendono fra l'altro la determinazione di figure piane in base a equazioni nelle quali intervengono sia aree sia lati, oppure la sola area, la suddivisione dell'area di un trapezio isoscele, e calcoli relativi a cerchi circoscritti e inscritti.

Il cap. 8, Procedimenti per gli scavi, è dedicato ai volumi delle figure solide, ossia scavi, pile di mattoni e taglio di tronchi, di solito trattati come procedimenti separati.

Il cap. 9, Procedimenti delle ombre, verte sulla determinazione delle direzioni (caso raro in un testo di matematica), delle ombre agli equinozi, della lunghezza dell'ombra in rapporto all'ora, e dei problemi riguardanti lo gnomone e la sua ombra.

In una certa misura la matematica di Mahāvīra fu influenzata dal suo credo jaina. Per esempio, i nomi delle posizioni decimali sono quelli tradizionali delle opere canoniche jaina, come l'Aṇuogaddāra (Le porte della disquisizione). La notazione parola/numero contiene tipici termini jaina, come kaṣāya ('attaccamento agli oggetti terreni') = 4, tattva ('principî elementari') = 7, e così via. Alcuni degli argomenti da lui trattati, come l'area di una figura piana a forma di conchiglia, hanno origine in trattati canonici jaina.

Āryabhaṭa II

La datazione di Āryabhaṭa II, autore del trattato astronomico Mahāsiddhānta (Grande siddhānta), è controversa. I confronti testuali inducono a pensare a un'epoca anteriore a quella di Bhāskara II, quindi in genere al X sec., ma una ricerca statistica sui parametri astronomici da lui usati, basata sul metodo dei minimi quadrati, sposta la datazione al 1500 circa (Billard 1971; Mercier 1993).

Due dei 18 capitoli della sua opera, pervenuta integralmente, sono consacrati alla matematica, il cap. 15, Algoritmi, in 120 versi, e il cap. 18, Polverizzatore, in 70 versi. Il primo abbraccia l'intero ambito dell'aritmetica, tratta le operazioni fondamentali (inclusi gli otto calcoli aritmetici con numeri interi, frazioni e zero e calcoli basati sulle proporzioni) e gli otto tipi di matematica per usi pratici. Il secondo, diversamente dall'omonimo capitolo del Brāhmasphuṭasiddhānta (Siddhānta corretto di Brahmagupta), tratta quasi esclusivamente dell'argomento indicato dal titolo, cioè il polverizzatore e le sue applicazioni in astronomia, tranne negli ultimi quattro versi, che forniscono metodi di verifica dei risultati di calcoli aritmetici.

Nel cap. 16, discutendo delle dimensioni della Terra, l'autore enuncia la formula corretta per l'area S della superficie di una sfera, S=cd, dove d è il diametro e c la circonferenza di un cerchio massimo.

Śrīpati

Attivo all'incirca tra il 1039 e il 1056 nel Maharashtra, Śrīpati fu un autore prolifico nell'ambito delle scienze astrali (jyotiḥśāstra) e della matematica. Come la Triśatikā (Libro in trecento versi) di Śrīdhara e il cap. 15 del Mahāsiddhānta di Āryabhaṭa II, il suo Gaṇitatilaka (Ornamento della matematica) è un testo sugli algoritmi nel quale sono affrontati i consueti argomenti relativi alle operazioni fondamentali e alla matematica per usi pratici. Il trattato di Śrīpati sull'algebra (bījagaṇita), menzionato da Munīśvara (n. nel 1603), non si è conservato, ma il testo astronomico di cui egli è autore, il Siddhāntaśekhara (Corona dei siddhānta, 1040 ca.), include un capitolo su questo argomento (cap. 14, Avyaktagaṇita, Matematica delle incognite) e uno sull'aritmetica (cap. 13, Vyaktagaṇita, Matematica delle quantità note). In quest'ultimo capitolo Śrīpati, seguendo le orme di Brahmagupta, prende in esame le 20 operazioni fondamentali e gli otto tipi di matematica per usi pratici.

Il cap. 14 è importante per la storia dell'algebra poiché rappresenta uno stadio intermedio tra il cap. 18 del Brāhmasphuṭasiddhānta di Brahmagupta (628) e il Bījagaṇita (Matematica dei semi) di Bhāskara II (1150). Gli argomenti trattati sono, nell'ordine: (1) terminologia e moltiplicazione di incognite (dove le incognite sono indicate da nomi di colori, come kālaka, 'nero', e nīlaka, 'blu', oltre che con il termine yāvattāvat); (2) gli otto calcoli aritmetici con numeri positivi e negativi; (3) i quattro calcoli aritmetici con lo zero; (4) i sei calcoli aritmetici con i numeri irrazionali (introdotti da una definizione di numero irrazionale); (5) due serie di forme normali algebriche; (6) i 'quattro semi'; (7) il polverizzatore; (8) il 'quadrato moltiplicato'; (9) la fattorizzazione di numeri interi.

I 'quattro semi' sono le 'equazioni a un colore' (di primo grado), le 'equazioni a più colori', l''eliminazione del termine medio' e le 'equazioni con prodotto'. Essi erano già stati trattati nel cap. 18 dell'opera di Brahmagupta; un commento anonimo a questo capitolo riporta la stessa serie di 'quattro semi', ma non è certo che sia stato Brahmagupta a raggrupparli e farne un unico concetto.

La fattorizzazione è invece un nuovo capitolo aggiunto da Śrīpati. Egli considera due metodi. Il primo consiste nel vedere se il numero è divisibile per 2, per 3, per 5, ecc. Il secondo è il seguente: se il numero è un quadrato, la sua radice è un divisore, ma se il numero non è un quadrato, per esempio n=a²+r(con r>0), se esiste un numero b tale che 2a+1−r=b², allora n=(a+1+b)(a+1−b).

Jayadeva

Nulla si sa di questo autore, ma 20 versi contenenti il metodo cakravāla ('ciclico') per l'equazione 'natura del quadrato' Px²+t=y² sono citati da Udayadivākara nel commento Sundarī (La bella, databile al 1073) al Laghubhāskarīya (Trattato conciso di Bhāskara). I primi sette versi, insieme ai relativi commenti di Udayadivākara, sono citati da Śaṅkara Vāriyar nel commento (1540 ca.) alla Līlāvatī. L'attività di Jayadeva sembra collocarsi in un'epoca di poco anteriore a Śrīpati (attivo tra il 1039 e il 1056); questi, discutendo dell'equazione 'natura del quadrato', non parla infatti del metodo ciclico.

Il cakravāla è un metodo ricorsivo che, con l'ausilio del polverizzatore, fornisce una soluzione dell'equazione per qualunque t a partire da una soluzione per t=±4, ±2 o ±1. Combinato con la regola di Brahmagupta, questo metodo fornisce una soluzione dell'equazione per t=1 (equazione di Pell).

Bhāskara II

Bhāskara II nacque nel 1114 in una famiglia di studiosi e letterati. Visse a Vijjaḍaviḍa alle falde del monte Sahya, situato all'estremità settentrionale dei Ghati occidentali, e completò la sua opera più importante, il Siddhāntaśiromaṇi (Diadema dei siddhānta), all'età di 36 anni. Bhāskara II è l'autore anche di un manuale di astronomia, il Karaṇakutūhala (Meraviglia dei Karaṇa), nel 1183, e di un commento (di data ignota) allo Śiṣyadhīvṛddhidatantra (Opera per l'accrescimento delle conoscenze degli studenti) di Lalla. Il Siddhāntaśiromaṇi si compone di quattro parti, due sulla matematica, la Līlāvatī (La giocosa) e il Bījagaṇita (Matematica dei semi), e due sull'astronomia, il Grahagaṇitādhyāya (Capitolo sui calcoli riguardanti i pianeti) e il Golādhyāya (Capitolo sull'astronomia sferica), che vengono spesso considerate come opere indipendenti.

Il Bījagaṇita segna l'apice dell'algebra indiana. È organizzato in maniera più sistematica del cap. 14 del Siddhāntaśekhara di Śrīpati e consta di una parte introduttiva e di una principale. La parte introduttiva contiene, nell'ordine: (1) le sei operazioni aritmetiche con numeri positivi e negativi; (2) le operazioni con lo zero; (3) quelle con i colori (le incognite); (4) quelle con i numeri irrazionali; (5) il polverizzatore; (6) l'equazione 'natura del quadrato'. Queste sono le conoscenze richieste per lo studio della 'quaterna di semi' (bīja-catuṣṭaya) trattata nella parte principale. Nell'algebra le quantità negative sono ammesse sia per i coefficienti delle equazioni sia per le loro soluzioni; infatti gli esempi di Bhāskara II relativi al polverizzatore comprendono y=(−60x±3)/13 e y=(18x±10)/(−11). Nel paragrafo sullo zero Bhāskara II paragona le proprietà di una frazione che ha zero a denominatore a quelle di Dio: è infinita, e non varia aggiungendo o togliendo una quantità finita. Il polverizzatore, che per Brahmagupta s'identificava con l'algebra, è qui soltanto uno degli strumenti per lo studio delle equazioni. Più importanti, secondo Bhāskara II, sono l'equazione 'natura del quadrato' e il metodo ciclico di Jayadeva. Il quarto degli esempi relativi a questa equazione, 61x²+1=y², coincide con il problema posto da Fermat nella lettera del 1657 a Frénicle.

La parte principale tratta della 'quaterna di semi' in cinque paragrafi: (1) equazioni a un colore (equazioni di primo grado a un'incognita); (2) eliminazione del termine medio per equazioni a un colore (equazioni di secondo grado a un'incognita); (3) equazioni a più colori (sistemi di equazioni a più incognite); (4) eliminazione del termine medio per equazioni a più colori; (5) equazioni con un prodotto delle incognite (equazioni del tipo axy=bx+cy+d).

Gli argomenti dei paragrafi (1), (2), (3) e (5) sono quelli tradizionali già trattati da Brahmagupta e Śrīpati, ma il paragrafo (4) rappresenta il più importante contributo di Bhāskara II all'algebra; qui egli esamina diversi tipi di equazioni di secondo grado o superiore (fino a sei) a più incognite, fornendo le relative soluzioni o indicandone di possibili. Bhāskara II prescrive regole per equazioni del tipo: ax²+bx+c=u², ax⁴+bx²=u², ax⁶+bx⁴=u², ax²+bx+c=a′y²+b′y+c′, ecc. Gli esempi che egli porta sono: x²+y²+z²+u²=x³+y³+z³+u³, x²+y²=u³ e x³+y³=u² (tutti e due insieme), x³+12x=6x²+35, ecc. Il titolo del paragrafo 'eliminazione del termine medio' indica che la soluzione delle equazioni di ordine più elevato avviene per lo più mediante la riduzione a equazioni di secondo grado, ma svolgono un ruolo molto importante anche l'equazione 'natura del quadrato' e il polverizzatore.

All'inizio della parte principale del Bījagaṇita, Bhāskara II fa riferimento al concetto tradizionale di 'quaterna di semi', in cui i 'semi' sono equazioni algebriche; nell'apertura dell'opera, tuttavia, l'autore afferma che "il seme [cioè il fondamento] della matematica delle quantità note menzionato in precedenza [cioè, nella Līlāvatī] è la matematica delle quantità incognite".

Qui ci si riferisce a un altro significato di 'seme', bīja, ossia alla stessa matematica delle equazioni, bīja-gaṇita, vista come il seme che genera la matematica degli algoritmi, pāṭī-gaṇita. Bhāskara II attribuisce al bīja anche il significato di intelligenza (mati o dhī). In diversi passi della sua opera afferma che "pāṭī ['algoritmo'] è la regola del tre, e bīja ['equazione'] è intelligenza senza macchia" e che "la sola intelligenza è bīja, perché il potere del pensiero è enorme".

Bhāskara II è noto anche per aver usato un rapporto equivalente al differenziale d(sinθ)=cosθdθ nel calcolo della velocità istantanea dei pianeti.

Ṭhakkura Pherū

Uno studioso jaina di nome Ṭhakkura Pherū (attivo nel 1315), figlio di Canda della famiglia Dhaṃdha, scrisse libri in pracrito su matematica, astronomia, architettura e gemmologia. Il testo sulla matematica, il Gaṇitasāra (Essenza della matematica), consta di quattro capitoli e un supplemento. I primi tre capitoli sono consacrati agli argomenti tradizionali degli algoritmi e denotano l'influenza di Śrīdhara: i 25 calcoli fondamentali con i numeri interi, le frazioni e lo zero, e con le proporzioni (cap. 1), le 8 classi di calcoli con le frazioni (cap. 2) e gli 8 tipi di matematica per usi pratici (cap. 3). Il cap. 4 e il supplemento includono argomenti nuovi, come i quadrati magici.

Apparentemente Ṭhakkura Pherū è stato il primo in India a fornire metodi generali per la costruzione di quadrati magici. La sua trattazione, pur concisa (soltanto nove versi), comprende la classificazione dei quadrati magici in tre tipi a seconda dell'ordine (cioè del numero n di caselle su un lato del quadrato), ossia, 'dispari' (viṣama), 'pari' (sama, in cui n è divisibile per 4) e 'pari-dispari' (samaviṣama, in cui n è divisibile per 2 ma non per 4). ṭhakkura Pherū fornisce un metodo generale per costruire i quadrati pari e uno per quelli dispari, mentre per i quadrati pari-dispari dà soltanto l'esempio di un quadrato di ordine 6.

Nārāyaṇa Paṇḍita

Nārāyaṇa, figlio di Narasiṃha, completò il suo trattato sugli algoritmi, la Gaṇitakaumudī (Luce lunare sulla matematica), il 14 ottobre del 1356. Scrisse anche un testo sulla matematica delle equazioni, intitolato Bījagaṇitāvataṃsa (Ghirlanda della matematica dei semi). Per la Gaṇitakaumudī Nārāyaṇa adotta apparentemente l'impostazione di Bhāskara II nella Līlāvatī, perché si ha una suddivisione in: (1) termini tecnici (inclusi i nomi delle 18 posizioni decimali); (2) 8 calcoli fondamentali; (3) regole varie; (4) matematica per usi pratici (vyavahāra). La matematica per usi pratici di Nārāyaṇa comprende però, oltre agli argomenti abituali, anche il polverizzatore, l'equazione 'natura del quadrato', l'acquisizione di parti (bhāga-ādāna), cioè la fattorizzazione, la manifestazione di frazioni (aṃśa-avatāra) o partizioni, le catene di cifre e la matematica dei quadrati magici (bhadra-gaṇita). Il modo in cui sono stati trattati gli ultimi quattro argomenti, a partire dalla fattorizzazione, ha una particolare importanza. Nessuno di essi è nuovo, ma qui sono trattati più estesamente e approfonditamente.

Il Bījagaṇitāvataṃsa, modellato sul Bījagaṇita di Bhāskara II, ha una parte introduttiva i cui contenuti corrispondono grosso modo a quelli del Bījagaṇita, a eccezione di alcune regole, che sono migliorate o aggiunte; per esempio, nella parte dedicata all'equazione 'natura del quadrato', è enunciata una regola per ottenere una radice quadrata approssimata: se Pa²+1=b², allora P^1/2≈b/a. L'altra sezione, la più importante, non è stata ancora studiata interamente, ma stando ai versi iniziali, l'argomento principale è la stessa 'quaterna di semi' del Bījagaṇita.

I secoli XV-XVII: la nuova scuola dell'India meridionale

L'India meridionale vide fiorire tra il XV e il XVII secolo numerosi matematici e astronomi di talento. Di particolare rilevanza è la tradizione accademica che ebbe come capostipite Mādhava di Saṅgamagrāma (attivo fra il 1380 e il 1420), spesso denominata scuola di Mādhava. Questi fu maestro di Parameśvara (attivo fra il 1380 e il 1460), che fu maestro del figlio, Dāmodara (attivo intorno al 1450), il quale a sua volta ebbe come discepoli Nīlakaṇṭha (1444 - m. dopo il 1542), Jyeṣṭhadeva (attivo fra il 1500 e il 1575 ca.) e Śaṅkara Vāriyar (attivo negli anni 1540-1556).

Mādhava di Saṅgamagrāma

Mādhava, abitante a Saṅgamagrāma presso Cochin, in Kerala, fu uno dei più brillanti matematici del mondo. Il suo nome è ricordato se non altro per la scoperta di uno sviluppo in serie di potenze di π e forse anche per quella delle principali funzioni trigonometriche. I versi che riguardano queste serie non figurano nei testi astronomici di Mādhava che ci sono pervenuti, ma in opere successive.

Śaṅkara Vāriyar attribuisce esplicitamente a Mādhava la formulazione dei due metodi per il calcolo della lunghezza della circonferenza di un dato cerchio. Utilizzando il primo di essi è possibile calcolare il perimetro dei poligoni regolari con 2ⁿ lati circoscritti al cerchio, per n 2, ossia a partire dal quadrato circoscritto. Il secondo dà la seguente formula: c=4d−(4d/3)+(4d/5)−···+ +(−1)ⁿ⁻¹[4d/(2n−1)]+(−1)ⁿ[4dn/(4n²+1)], in cui d è il diametro e l'ultimo termine è un termine correttivo. Se si dividono entrambi i membri di questa formula (senza il termine correttivo) per 4d, si ottiene la serie per π/4 che Leibniz avrebbe scoperto 270 anni più tardi (1673 ca.). Śaṅkara Vāriyar fornisce una dimostrazione della formula, basata sulla proprietà per cui un arco piccolo è approssimativamente uguale al proprio seno (moltiplicato per il raggio). Nel corso della dimostrazione, si serve della somma aq/p=Σ_i(−1)ⁱa(p−q)ⁱ/qⁱ, per i che va da 0 a ∞, e dell'approssimazione aΣ_n(na)ⁱ≈(ma)ⁱ⁺¹/(i+1), per n che va da 1 a m. Egli dà anche le seguenti uguaglianze:y=θ−θ×θ²/(2²+2)R²+θ×[θ²/(2²+2)R²]×[θ²/(4²+4)R²]+ −… e θ=(Ry/x)−[Ry³/(3x³)]+[Ry⁵/(5x⁵)]−…, dove θ è l'arco di un cerchio di raggio R e x=Rcosθ, y=Rsenθ. È probabile che molte di queste formule risalgano allo stesso Mādhava.

Śaṅkara Vāriyar cita la strofa di Mādhava che esprime, con la notazione parola-numero, un'ottima approssimazione per π con 11 cifre decimali, 2.827.433.388.233/ (9×10¹¹)=3,141 592 653 59… (il valore di π è 3,141 592 653 58…). Nīlakaṇṭha, suo maestro, si riferisce al medesimo verso nel commento all'Āryabhaṭīya (Trattato di Āryabhaṭa) e inoltre cita i versi di Mādhava che esprimono, con la notazione kaṭapayādi, una tavola dei seni per (in notazione sessagesimale) R=3438;44,48 (cioè 3438+44/60+ +48/3600). Essa contiene 24 'seni maggiori' (mahā-jyā), cioè Rsen(225i) per i=1, 2, …, 24, calcolato fino alla seconda posizione sessagesimale. Esiste un breve commento anonimo intitolato Mahājyānayanaprakāra (Metodo per il calcolo dei seni maggiori) in tre versi, probabilmente di Mādhava. Nīlakaṇṭha cita anche, dimostrandola, la formula d'interpolazione di Mādhava, equivalente all'approssimazione del secondo ordine della serie di Taylor: Rsen(225i+θ)≈J_i+(2/D)×(J₂₄₋i−J_i/D) e Rcos(225i+θ)≈J_24−i+ −(2/D)×(J_i−J_24−i/D), dove J_i=Rsen(225i), θ è un arco minore di 225° (con il valore per R dato sopra, l'intera circonferenza vale circa 21.600) e D=4R/2θ≈13751/(2θ); si noti che J_24−i=Rcos (225i).

Nīlakaṇṭha Somayāji e altri

Nīlakaṇṭha, figlio di Jātavedas, nacque intorno al 14 giugno 1444 a Kuṇḍapura presso Tirur, in Kerala, e fu discepolo di Dāmodara ad Ālattūr, nella stessa regione; morì dopo il 1542. Scrisse brevi trattati di astronomia, tra cui il Golasāra (Essenza dell'astronomia sferica), il Siddhāntadarpaṇa (Specchio dell'esposizione conclusiva) e il Candracchāyāgaṇita (Matematica delle ombre della Luna), e compose anche un'opera più estesa, il Tantrasaṃgraha (Compendio della dottrina [astronomica]), in otto capitoli, nel 1501.

A lui si deve un elaborato commento all'Āryabhaṭīya, composto verso il 1510, che dimostra il suo grande talento sia in campo matematico sia astronomico. Per fare soltanto alcuni esempi, Nīlakaṇṭha riscoprì il vero significato della regola di Āryabhaṭa per le differenze dei seni. Afferma esplicitamente l'incommensurabilità della circonferenza e del diametro di un cerchio, come dire l'irrazionalità del loro rapporto π‚ anche se non si sa se l'abbia dimostrata; inoltre, cita e dimostra le formule di Mādhava per l'interpolazione nella tavola dei seni e per la somma e la differenza dei seni.

Nel Golasāra (3.9) Nīlakaṇṭha enuncia una formula per l'ampiezza θ di un arco di cerchio, θ≈[J²+(4I²/3)]^1/2, dati J=Rsenθ e I=R−Rcosθ (si tratta di un'ottima approssimazione per un arco minore di 15°). Questa formula è dedotta nel commento all'Āryabhaṭīya mediante successive bisezioni dell'arco, ricorrendo alla proprietà secondo la quale il senoverso di un arco è approssimativamente uguale a un quarto di quello di un arco di grandezza doppia, e inoltre a una formula per la somma di una progressione geometrica infinita.

La sua Jyotirmīmāṃsā (Riflessione sull'astronomia) occupa un posto unico nell'astronomia indiana perché vi è esposta una metodologia di tale scienza. Nīlakaṇṭha condanna le spiegazioni mitologiche dei fenomeni astronomici e sottolinea l'importanza dell'osservazione: è sulla base di questa che le teorie e i calcoli astronomici devono essere controllati e corretti.

Śaṅkara Vāriyar, allievo di Nīlakaṇṭha, è autore di numerosi commenti a trattati di astronomia e di matematica. La sua fama è dovuta più a questi testi che al manuale di astronomia, il Karaṇasāra (Essenza dei Karaṇa), che scrisse intorno al 1554. Il suo commento (1540 ca.) alla Līlāvatī (La giocosa) di Bhāskara II è ricco d'informazioni e contiene numerose citazioni dalle opere dei maggiori matematici a lui precedenti.

A Śaṅkara Vāriyar si deve anche la realizzazione della Yuktidīpikā (Illustrazione del ragionamento, 1530 ca.), un commento in versi ai primi quattro capitoli del Tantrasaṃgraha di Nīlakaṇṭha, basata sulla Yuktibhāṣā (Discorso sul ragionamento) di Jyeṣṭhadeva, opera in lingua malayalam, concepita come un'esposizione del ragionamento (o fondamento logico) delle teorie astronomiche enunciate nel Tantrasaṃgraha e dell'apparato matematico su cui si basano. Essa contiene, tra l'altro, la spiegazione delle formule per l'area della superficie, S=cd, e per il volume, V=Sd/6, di una sfera. L'autore decompone la sfera in un certo numero di corone circolari, nel primo caso, e in un certo numero di dischi, nel secondo. Le dimostrazioni sono caratterizzate dall'uso della proprietà secondo la quale il seno è proporzionale alla differenza delle differenze dei seni, (K_i−K_i+1)/J_i=(a/R)² (v. par. 4), e della somma approssimata della serie dei quadrati, Σi²≈n³/3, per i che va da 1 a n.

La matematica indiana ebbe dunque un proprio, eccezionale sviluppo fino al XVII secolo. Fu soltanto negli anni Venti del sec. XVIII che Jagannātha (1652-1744), su richiesta di Jai Singh Sawai (1688-1744) suo mecenate, tradusse in sanscrito gli Elementi di Euclide con il titolo Rekhāgaṇita (Matematica delle rette). Per la compilazione di quest'opera, Jagannātha si basò sulla versione araba di Naṣīr al-Dīn al-Ṭūsī.

Bibliografia

Alsdorf 1974: Alsdorf, Ludwig, Die Pratyayas. Ein Beitrag zur indischen Mathematik, in: Kleine Schriften, Wiesbaden, Steiner, 1974, pp. 600-660 (1. ed.: "Zeitschrift für Indologie und Iranistik", 9, 1933, pp. 97-157).

Bag 1979: Bag, Amulya Kumar, Mathematics in ancient and medieval India, Varanasi, Chaukambha Orientalia, 1979.

Billard 1971: Billard, Roger, L'astronomie indienne. Investigation des textes sanskrits et des données numériques, Paris, École Française d'Extrême-Orient, 1971.

Datta 1983: Datta, Bibhutibhusan - Singh, Avadesh Narayan, Hindu trigonometry, revised by Kripa S. Shukla, "Indian journal of history of science", 18, 1983, pp. 39-108.

Gupta 1967: Gupta, Radha Charan, Bhāskara I's approximation to sine, "Indian journal of history of science", 2, 1967, pp. 121-136.

‒ 1969: Gupta, Radha Charan, Second order interpolation in Indian mathematics up to the fifteenth century, "Indian journal of history of science", 4, 1969, pp. 86-98.

Hayashi 1989: Hayashi, Takao - Kusuba, Takanori - Yano, Michio, Indian values for π derived from Āryabhaṭa's value, "Historia scientiarum", 37, 1989, pp. 1-16.

Ifrah 1981: Ifrah, Georges, Histoire universelle des chiffres. Lorsque les nombres racontent les hommes, Paris, Seghers, 1981 (trad. it.: Storia universale dei numeri, Milano, Mondadori, 1983).

Joseph 1991: Joseph, George G., The crest of the peacock. Non-European roots of mathematics, London-New York, I.B. Tauris, 1991 (trad. it.: C'era una volta un numero. La vera storia della matematica, Milano, Il Saggiatore, 2000).

Pingree 1970-94: Pingree, David, Census of the exact sciences in Sanskrit, series A, Philadelphia, American Philosophical Society, 1970-; v. I-V: 1970-1994.

‒ 1978: Pingree, David, History of mathematical astronomy in India, in: Dictionary of scientific biography, edited by Charles C. Gillispie, New York, Scribner, 1970-1980, 16 v.; v. XV: 1978, pp. 533-633.

‒ 1981: Pingree, David, Jyotiḥśāstra. Astral and mathematical literature, Wiesbaden, O. Harrassowitz, 1981.

‒ 1992: Pingree, David, On the date of the Mahāsiddhānta of the second Āryabhaṭa, "Gaṇita Bhāratī", 14, 1992, pp. 55-56.

Qian 1990: Qian, Baocong, Zhongguo shuzue shi [A history of Chinese mathematics], Beijing, Xinhua shudian, 1964 (trad. giapp.: Chūgoku sūgaku shi, trad. di Hideki Kawahare, Tokyo, 1990).

Rajagopal 1986: Rajagopal, Cadambur T. - Rangachari, M.S., On medieval Kerala mathematics, "Archive for history of exact sciences", 35, 1986, pp. 91-99.

Rosu 1989: Rosu, Arion, Les carrés magiques indiens et l'histoire des idées en Asie, "Zeitschrift der Deutschen Morgenländischen Gesellschaft", 139, 1989, pp. 120-158.

Sarasvati Amma 1979: Sarasvati Amma, T.A., Geometry in ancient and medieval India, Delhi, Motilal Banarsidass, 1979.

Sarma 1972: Sarma, K. Venkateswara, A history of the Kerala school of Hindu astronomy (in perspective), Hoshiarpur, Vishveshvaranand, 1972.