serie di funzioni, criteri di convergenza per una

serie di funzioni, criteri di convergenza per una

serie di funzioni, criteri di convergenza per una condizioni necessarie e/o sufficienti per stabilire la convergenza di una serie di funzioni.

Il criterio di convergenza di Cauchy per una serie di funzioni stabilisce che condizione necessaria e sufficiente perché una serie di funzioni sia convergente per un valore x della variabile è che per ogni numero ε > 0 prefissato esista un indice N, dipendente da ε ed eventualmente da x, tale che per n ≥ N e per ogni p ≥ 0 sia:

formula

Se tale condizione è soddisfatta per ogni x di un intervallo (a, b) del dominio D delle funzioni con un indice N indipendente da x, allora la serie è uniformemente convergente. Una serie uniformemente convergente in un intervallo (a, b) è assolutamente convergente in ogni punto di (a, b).

Una serie di funzioni si dice totalmente convergente in (a, b) se la serie delle norme dei suoi termini,

formula

è convergente. Una serie totalmente convergente in (a, b) è uniformemente convergente in tale intervallo.

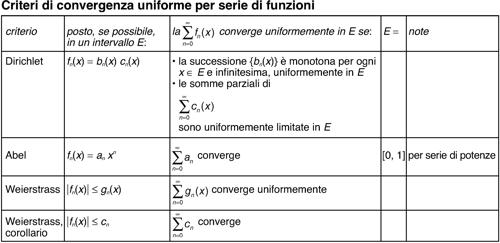
I criteri di convergenza per le serie di funzioni non differiscono da quelli per le serie numeriche. Criteri particolari si stabiliscono per la convergenza uniforme; in particolare il criterio di → Weierstrass per l’uniforme convergenza di una serie di funzioni (si veda la tavola dei criteri di convergenza uniforme per una serie di funzioni).