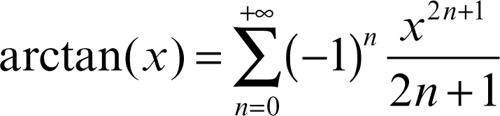Gregory-Leibniz, serie di
Gregory-Leibniz, serie di
Gregory-Leibniz, serie di in analisi, sviluppo di → Maclaurin della funzione arcotangente:
valido nell’intervallo (−1, 1). Tale sviluppo, descritto da J. Gregory nel 1668, era già noto anche ai matematici indiani. Esso fu riscoperto da Leibniz nel caso particolare x = 1, che fornisce
Anche se il calcolo del quadruplo delle somme parziali di questa serie è uno dei metodi per la determinazione di valori approssimati di π, la sua lentissima convergenza non permette in realtà un calcolo accurato di π. Per questo furono escogitate diverse varianti, la più famosa delle quali è dovuta a John Machin (1680? - Londra 1751), che nel 1706 ne calcolò 100 cifre decimali attraverso una formula che da lui prende il nome. Per giungere alla formula di Machin si calcoli con la serie di Gregory-Leibniz il valore α = arctan(1/5):
Mediante le formule di duplicazione da tan(α) = 1/5 si ottiene tan(2α) = 5/12 e poi tan(4α) = 120/119 e quindi 4α è di poco maggiore di π/4. Posto allora β = 4α − π/4, risulta
da cui
Calcolati α e β si ha poi π = 4(4α − β). Questa è la formula di Machin, che può essere espressa anche come π = 4(4arctan(1/5) − arctan(1/239)).
Per apprezzare la rapidità di convergenza di queste serie si osservi che bastano sei addendi della prima serie e due della seconda (valutati con 9 cifre decimali per controllare gli errori di arrotondamento) per ottenere sette cifre decimali di π.