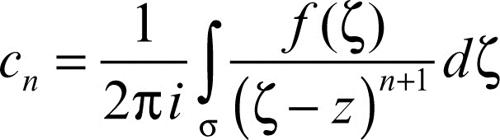Laurent, serie di
Laurent, serie di
Laurent, serie di serie di potenze positive o negative di z − z0 in cui si sviluppa una funzione analitica ƒ(z), olomorfa in una corona circolare Ω di centro z0. L’espressione della serie è:
A essa si dà il nome di sviluppo in serie di Laurent della funzione ƒ(z). I coefficienti cn si ottengono, per ogni n ∈ Z, dalle formule
dove σ è un qualsiasi ciclo contenuto in Ω, percorso in verso antiorario. Se il raggio minore della corona si riduce a 0, per cui la corona costituisce un intorno di z0, escluso il punto stesso, la serie
si chiama componente olomorfa di ƒ in z0, mentre
si chiama componente caratteristica o semplicemente caratteristica. La caratteristica permette di classificare la singolarità di ƒ in z0: se tutti i coefficienti di indice negativo sono nulli, e quindi I2(z) = 0, non vi è singolarità; se solo un numero finito è diverso da zero, la caratteristica si riduce a un polinomio di → Laurent e z0 è un polo per ƒ; se infiniti coefficienti sono nulli, z0 è una singolarità essenziale per ƒ.
La serie di Laurent relativa al punto all’infinito è uno sviluppo di ƒ della forma
convergente per |z| > R; in questo caso la caratteristica è formata dalle potenze con esponente n > 0. Se una funzione possiede un numero finito di singolarità, essa è somma delle relative componenti caratteristiche, più una costante.