Maclaurin, serie di

Maclaurin, serie di

Maclaurin, serie di caso particolare della serie di → Taylor, in cui il centro è nell’origine. La sua importanza consiste nel fatto che, per la sua semplicità strutturale, le più importanti funzioni ammettono semplici sviluppi in serie di Maclaurin, tramite i quali è possibile costruire gli sviluppi di moltissime funzioni mediante operazioni algebriche e di composizione. Molte serie di Taylor con centro in un punto generico possono infatti essere ridotte a opportune serie di Maclaurin e, quindi, non necessitano del calcolo di derivate per la determinazione dei loro coefficienti. Per esempio, se si desidera la serie di Taylor di ln(3 + 2x) nell’intorno del punto x = 1, basta eseguire una trasformazione quale la seguente:

per ricondurne lo sviluppo a quello di ln(1 + z), con z = 2(x − 1)/5, sviluppabile in serie di Maclaurin. Si avrà dunque:

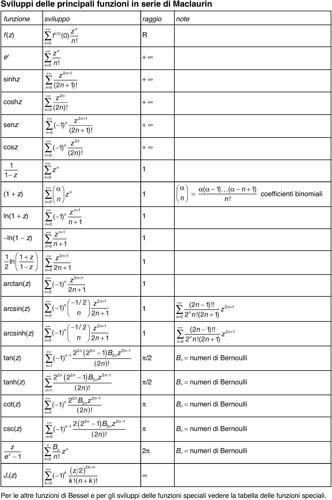
Per gli sviluppi in serie di Maclaurin si veda la relativa tavola.