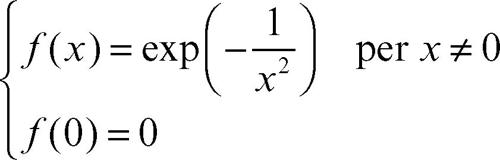Taylor, serie di

Taylor, serie di

Taylor, serie di per una funzione di variabile reale ƒ(x): R → R, dotata di derivate di ogni ordine in un punto x₀, è la → serie di potenze

Sotto opportune ipotesi essa converge a ƒ(x) in un intervallo (x₀ − h, x₀ + h), detto intervallo di convergenza: per esempio, si può richiedere che le derivate soddisfino in tale intervallo la condizione |ƒ⁽ⁿ⁾(x)|/n! ≤ M /hⁿ, con M costante. Si dice allora che ƒ(x) è sviluppabile in serie di Taylor in un intorno di x₀. Esistono funzioni di classe C ^∞ non sviluppabili, o perché la loro serie di Taylor non converge per nessun x ≠ x₀, oppure perché converge ma non alla funzione generatrice: per esempio la funzione così definita

è dotata nell’origine di derivate di ogni ordine, che però sono tutte nulle, per cui la sua serie di Taylor converge alla funzione identicamente nulla.

La serie di Taylor permette di estendere al campo complesso la definizione di funzione reale. Basta infatti porre la variabile complessa z al posto della variabile reale x per ottenere una serie di potenze, il cui cerchio di convergenza ha raggio almeno h. In particolare, se h è arbitrario, si ha che il raggio R è ∞ e si ottiene una trascendente intera. Per esempio, dallo sviluppo di e^x, valido su tutto R, si ottiene la definizione della funzione esponenziale e^z in tutto C. Le funzioni ottenute con questo metodo di → prolungamento dal reale al complesso godono automaticamente della proprietà di essere funzioni analitiche e sono l’unica estensione analitica della funzione reale data. Se l’intervallo di convergenza della serie reale era limitato, la serie prolungata ammetterà sulla circonferenza di convergenza dei punti singolari, e può risultare polidroma. Per esempio, lo sviluppo di ƒ(x) = arctan(x) si estende e definisce arctan(z) come somma della serie

ma tale sviluppo vale solo nel cerchio |z| < 1, pur essendo la funzione ƒ(x) di classe C^∞ (R). Il motivo sta nel fatto che la derivata di ƒ(z) è 1/(1 + z ²) e questa funzione, regolare in R, non lo è in C, ammettendo due poli semplici nei punti z = ±i. La loro presenza impone che sia R = 1, non potendo esistere singolarità di una funzione analitica all’interno del suo cerchio di convergenza. Si noti inoltre che arctan(z) è funzione polidroma, definita in C{±i } (si tratta di due punti di diramazione): lo sviluppo precedente ne fornisce solo la parte principale nel cerchio di convergenza, mentre il resto della funzione può essere ottenuto mediante prolungamento analitico secondo Weierstrass (→ funzione analitica). In definitiva, una funzione è sviluppabile in serie di Taylor se e solo se è analitica: nell’esempio precedente, la funzione exp(−1/z ²) prolungata nel campo complesso non è continua nell’origine, dove presenta una singolarità essenziale e il suo sviluppo di Taylor è fittizio.