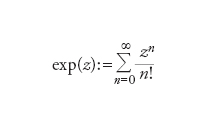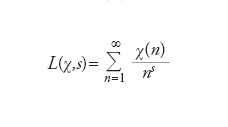serie L di Dirichlet
serie L di Dirichlet
Sia m un numero intero. Un carattere di Dirichlet modulo m è una funzione χ:ℕ→ℂ tale che: (a) χ(1)=1; (b) χ(p+m)=χ(p) per ogni p∈ℕ (si esprime questo fatto dicendo che χ ha periodo m); (c) χ(pq)=χ(p)χ(q) per ogni coppia (p,q) di numeri interi (si esprime questo fatto dicendo che χ è moltiplicativa in senso stretto); (d) χ(p)=0 se p e m non sono primi tra loro (cioè MCD(p;m)≠1). Se n è un numero naturale positivo e s è un numero complesso, si ponga: ns=exp(s log(n)). Nella formula precedente si è indicato con exp l’esponenziale complessa, definita per ogni numero complesso z dalla serie convergente
dove n!=(n−1)∙∙∙2∙1 indica il fattoriale del numero naturale n (con la convenzione usuale che 0! valga 1). Sia χ un carattere di Dirichlet modulo m. La funzione L di Dirichlet associata al carattere χ è la serie L(χ,s) definita nel modo seguente:
Usando il fatto che i numeri complessi χ(n) sono radici m-esime dell’unità per tutti gli interi n, si può dimostrare che la serie L(χ,s) è assolutamente convergente nel semipiano complesso {s∈ℂ tali che ✄(s)>1} formato dai numeri complessi s con parte reale ✄(s) maggiore di 1. Essa è inoltre convergente (non necessariamente assolutamente) nel semipiano {s∈ℂ tali che ✄(s)>0} formato dai numeri complessi con parte reale maggiore di 0. È noto infine che le funzioni L(χ,s) possono essere continuate analiticamente a funzioni meromorfe su tutto il piano complesso. Se χ è il carattere banale (cioè χ(n)=1 per tutti i numeri interi n), allora la funzione L di Dirichlet corrispondente è detta funzione zeta di Riemann ed è indicata con il simbolo ζ(s).