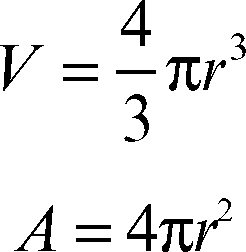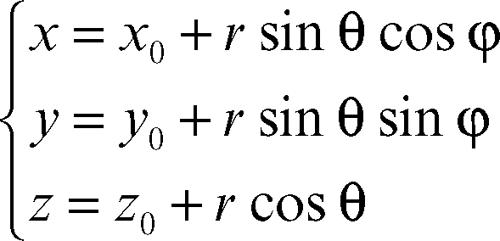sfera

sfera

sfera nell’ordinaria geometria dello spazio euclideo tridimensionale, luogo dei punti dello spazio aventi da un punto fisso C una distanza minore o uguale a una prefissata distanza r > 0. Il punto C è detto centro della sfera, la distanza r è detta raggio della sfera. Il termine raggio e il corrispondente simbolo r sono utilizzati sia per rappresentare la distanza tra il centro C e un qualsiasi punto P della superficie della sfera sia per rappresentare uno qualsiasi dei segmenti CP. Ogni segmento che congiunge due qualsiasi punti della superficie sferica è detto corda della sfera. Ogni corda passante per il centro C prende il nome di diametro e misura 2r. Un piano α, rispetto una sfera Σ di centro C e raggio r, è detto:

• esterno se la distanza tra α e C è maggiore di r. In tal caso α e Σ sono privi di punti comuni;

• tangente se la distanza tra α e C è uguale a r. In tal caso α e Σ hanno un punto doppio in comune;

• secante se la distanza tra α e C è minore di r. In tal caso α e Σ hanno in comune tutti i punti di un cerchio.

L’intersezione di un piano con una sfera è un cerchio. Se il piano secante passa per il centro della sfera si ottiene il cerchio di circonferenza massima della sfera (avendo il massimo raggio possibile, uguale a quello della sfera). Le circonferenze massime costituiscono le → geodetiche della sfera. Intersecando la sfera con un fascio di piani passanti per un suo diametro (corda massima della sfera, passante per il centro della sfera stessa) e con un fascio di piani perpendicolari al diametro, si ottiene un doppio sistema di curve: le prime (meridiani) sono cerchi massimi, mentre le seconde (paralleli) sono cerchi di raggio variabile; le curve dei due sistemi sono perpendicolari fra loro e sono atte a costituire un sistema di coordinate, che si dicono sferiche (→ coordinate sferiche).

Le misure del volume e della superficie di una sfera di raggio r sono rispettivamente

In coordinate cartesiane, una superficie sferica di centro C(x₀, y₀, z₀) e raggio r è una superficie quadrica rappresentata dall’equazione

mentre, in coordinate sferiche è rappresentata dalle equazioni

I piani e gli assi di simmetria di una sfera sono costituiti, rispettivamente, da tutti i piani e da tutte le rette passanti per il suo centro (centro di simmetria). Le coppie di punti simmetrici rispetto al suo centro sono detti punti antipodali.

Le due parti in cui una sfera è divisa da un piano sono dette segmenti sferici a una base (in particolare possono essere due semisfere o emisferi), mentre il piano individua sulla superficie due calotte sferiche; due piani paralleli che taglino una sfera ne staccano un segmento sferico a due basi e sulla superficie si determina una zona sferica. Un cono indefinito con il vertice nel centro della sfera individua nella sfera un solido detto settore sferico e la sua intersezione con la superficie sferica individua una calotta sferica; la parte di sfera staccata da un diedro avente come spigolo un diametro è uno spicchio sferico e la superficie corrispondente si dice fuso sferico. Tre archi di cerchi massimi, aventi a due a due un punto in comune, individuano sulla superficie un → triangolo sferico.

La nozione di superficie sferica viene generalizzata in dimensione n qualsiasi. In uno spazio euclideo di dimensione n + 1, viene detta sfera n-dimensionale di centro C e raggio r (così intendendo la superficie sferica) l’insieme dei punti aventi da C distanza r. Così, una sfera 0-dimensionale è una coppia di punti, simmetrici rispetto a C; su una retta, una sfera 1-dimensionale è una circonferenza, una sfera 2-dimensionale è una sfera ordinaria, una sfera 3-dimensionale è una sfera dello spazio euclideo 4-dimensionale, e così via. Se si vogliono considerare tutti i punti che hanno distanza minore o uguale a r, si preferisce utilizzare il termine palla.