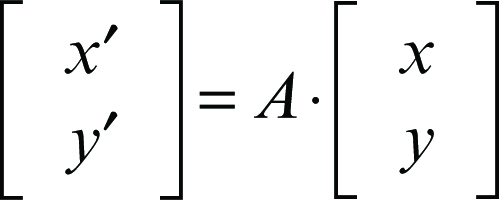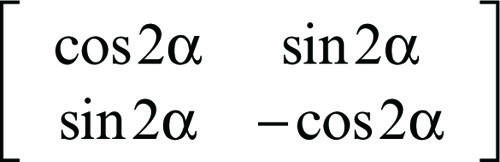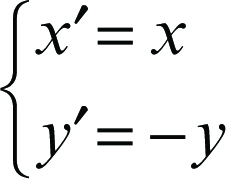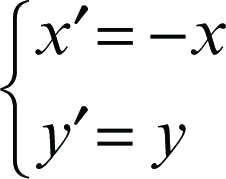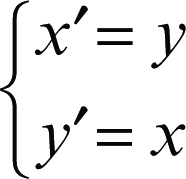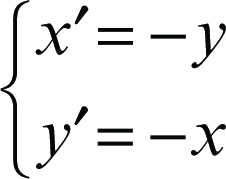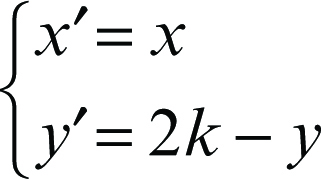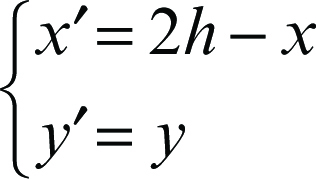simmetria assiale

simmetria assiale

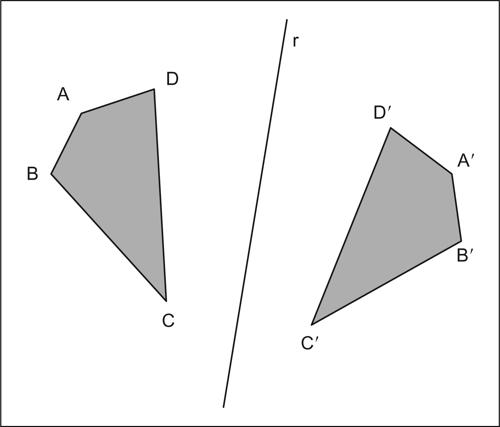
simmetria assiale detta anche riflessione se nel piano, ribaltamento se nello spazio tridimensionale, in geometria, particolare trasformazione isometrica del piano o, più in generale, di uno spazio di dimensione n ≥ 2, per cui, fissata una retta r, a ogni punto P corrisponde il punto P′ tale che r risulti l’asse del segmento PP′. La retta r è detta asse della simmetria. È una trasformazione involutoria (coincide con la propria inversa e composta con sé stessa dà l’identità) e invertente (modifica l’orientamento del piano). Essendo una → isometria, ne ha tutti gli invarianti. Tutti e soli i punti fissi della trasformazione sono i punti dell’asse di simmetria mentre le rette perpendicolari all’asse sono rette unite (corrispondono cioè a sé stesse, ma globalmente e non punto per punto). Nel piano, la composizione di due simmetrie assiali dà luogo a una → traslazione (se i due assi sono paralleli) oppure a una → rotazione (se i due assi sono incidenti). Se le rette r e r′, assi delle due simmetrie, sono parallele e a distanza d, il prodotto delle due simmetrie è una traslazione con vettore di modulo 2d. Se le rette r e r′ sono incidenti in un punto O e formano un angolo di ampiezza α, il prodotto delle due simmetrie è una rotazione di centro O e angolo di ampiezza 2α. Ogni isometria del piano può essere ottenuta componendo al più tre simmetrie assiali (teorema delle tre simmetrie). Nel piano dotato di un riferimento cartesiano Oxy la simmetria rispetto a una retta passante per l’origine, di equazione y = mx (e che quindi forma un angolo di ampiezza α = arctan(m) con l’asse delle ascisse), ha equazioni:

dove x′ e y′ sono le coordinate del punto corrispondente nella trasformazione e A è la matrice, con determinante uguale a −1,

In particolare, sono notevoli le seguenti simmetrie:

• simmetria rispetto all’asse delle ascisse:

• simmetria rispetto all’asse delle ordinate:

• simmetria rispetto alla bisettrice del i e iii quadrante:

• simmetria rispetto alla bisettrice del ii e iv quadrante:

• simmetria rispetto a una parallela all’asse x (di equazione y = k):

• simmetria rispetto a una parallela all’asse y (di equazione x = h):

Simmetria assiale obliqua

Trasformazione affine del piano per cui, assegnata una retta r (asse della simmetria obliqua) e una direzione d (né parallela né perpendicolare a r) a ogni punto P del piano corrisponde un punto P′ tale che il segmento PP′ abbia direzione d e intersechi la retta r nel suo punto medio (→ affinità). Anche in questo caso, tutti i punti dell’asse sono fissi mentre le rette unite (a parte l’asse) sono tutte e sole le rette di direzione d.