simmetria

simmetria

simmetria termine che indica una trasformazione geometrica del piano o dello spazio oppure la proprietà di una figura; per analogia, il termine è utilizzato anche in altri campi della matematica (differenza simmetrica: → differenza; gruppo simmetrico: → simmetria, gruppo di (di una figura); → matrice simmetrica; relazione simmetrica: → relazione; → sistema simmetrico). Una figura piana si dice simmetrica (assialmente, centralmente oppure per rotazione) se corrisponde a sé stessa in una simmetria (rispettivamente una → simmetria assiale, una → simmetria centrale o una → simmetria rotazionale). Un triangolo isoscele è per esempio una figura simmetrica assialmente (rispetto all’altezza relativa alla base), un triangolo equilatero è simmetrico rispetto a ognuna delle sue altezze, un cerchio è simmetrico assialmente rispetto a ognuno dei suoi diametri e quindi è simmetrico centralmente rispetto al suo centro. Ogni poligono regolare con un numero pari di lati è simmetrico assialmente (rispetto alle diagonali e agli assi dei lati opposti) e centralmente (rispetto al punto di intersezione delle diagonali). Ogni poligono regolare presenta inoltre una simmetria rotazionale. Il concetto di figura simmetrica si estende naturalmente allo spazio tridimensionale, in cui si considera anche la simmetria rispetto a un piano o → simmetria planare. La sfera, che è simmetrica centralmente, è anche simmetrica rispetto a ognuno dei piani che individuano una sua circonferenza massima. Il cubo è simmetrico centralmente ed è anche simmetrico rispetto a 9 piani di cui 3 passanti per i punti medi degli spigoli tra loro paralleli e 6 congiungenti le coppie di spigoli opposti.

Il termine figura simmetrica è utilizzato anche con un significato più generale, identificando i diversi tipi di simmetria. Nel piano si usa così dire che una figura piana è simmetrica di ordine n quando a essa è associato il → gruppo diedrale D_n, cioè il gruppo delle isometrie che trasformano la figura in sé stessa e in cui n è l’ordine del sottogruppo di D_n formato dalle sole rotazioni (→ isometria). Secondo questa terminologia, il pentagono regolare (come peraltro molti fiori in natura) risulta una figura simmetrica di ordine 5 e un solido nello spazio è simmetrico se ammette un gruppo non banale di isometrie che lo trasformano in sé stesso. Il gruppo delle isometrie di un poliedro regolare con ν vertici e k facce che concorrono in un vertice ha 2kν elementi. Così, il gruppo delle isometrie di un tetraedro regolare ha 24 elementi ed è isomorfo al gruppo simmetrico S₄, mentre il gruppo delle isometrie del cubo ha 48 elementi.

☐ In algebra, la simmetria o proprietà simmetrica è la proprietà di cui gode una → relazione, definita su un insieme A, quando, per ogni coppia a, b di elementi di A, se a è in relazione con b, allora anche b è in relazione con a. L’uguaglianza in un insieme numerico è per esempio una relazione simmetrica mentre non lo è la relazione < («essere minore»). Tutte le relazioni di → equivalenza sono per definizione simmetriche.

☐ In statistica, si parla di simmetria in relazione alla forma assunta da una → distribuzione di dati statistici.

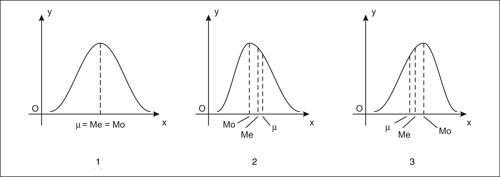
La distribuzione normale è una distribuzione simmetrica rispetto al suo valore centrale: se una distribuzione è simmetrica, allora moda (qui indicata con Mo), mediana (qui indicata con Me) e media aritmetica (indicata con μ) coincidono, ma non è vero l’inverso. Se una distribuzione non è simmetrica si distingue tra:

• distribuzione con asimmetria positiva, se

in tal caso un maggior numero di unità presenta le modalità di valore inferiore. Rispetto alla curva normale, il massimo è spostato verso sinistra;

• distribuzione con asimmetria negativa, se

in tal caso un maggior numero di unità presenta le modalità di valore superiore. Rispetto alla curva normale, il massimo è spostato verso destra.

In letteratura sono proposti diversi indici di asimmetria. Due indici assoluti sono dati dalle differenze

che sono positivi o negativi a seconda del corrispondente tipo di asimmetria. Un indice di asimmetria relativo proposto da K. Pearson, e perciò detto skewness di Pearson (skewness è il termine inglese per «asimmetria»), è il seguente:

in cui σ è lo → scarto quadratico medio. Questi indici, come altri proposti, hanno tuttavia il difetto di non garantire, se nulli, che la distribuzione sia simmetrica.