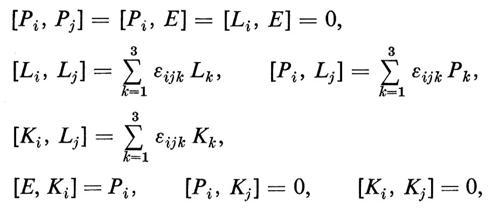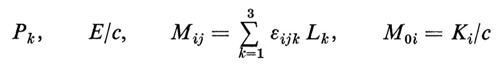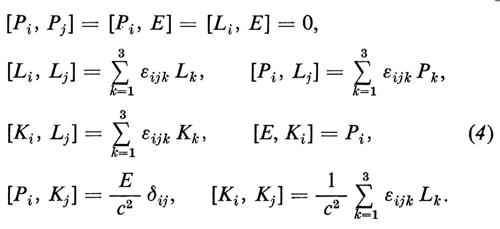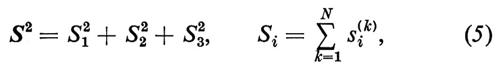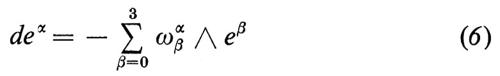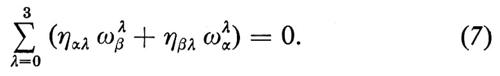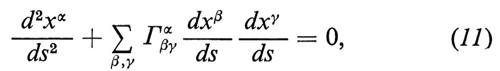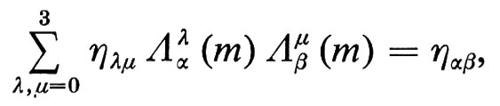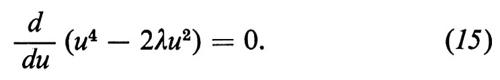Simmetrie e invarianze

Simmetrie e invarianze

di Luigi A. Radicati di Brozolo

SOMMARIO: 1. Introduzione e brevi cenni storici. □ 2. La struttura dello spazio-tempo assoluto. □ 3. Il ruolo della simmetria nella meccanica quantistica: a) considerazioni generali; b) la classificazione dei livelli atomici; c) l'invarianza relativistica e lo spin; d) la coniugazione di carica, l'inversione temporale, il teorema PCT. □ 4. Fisica e geometria: la concezione nemanniana. □ 5. Estensione dello schema geometrico: le simmetrie interne. □ 6. L'origine dell'asimmetria: a) la rottura spontanea della simmetria; b) biforcazioni con rottura di simmetria; c) la rottura spontanea della simmetria nelle teorie di gauge non abeliane; d) ordine e simmetria. □ 7. Conclusioni. □ Bibliografia.

1. Introduzione e brevi cenni storici.

Il concetto di simmetria interviene in contesti così diversi che è ben difficile trovare oggi riunite in una singola persona le competenze necessarie a discutere in maniera esauriente un tema che va dalle arti figurative alla musica, dalla matematica alle scienze naturali.

L'ultimo tentativo di abbracciare in un'unica visione i vari aspetti della simmetria fu probabilmente quello compiuto dal grande matematico H. Weyl (v., 1952), che, sul finire della vita, espose in un elegante libretto, dal titolo appunto Symmetry, che lui stesso definì il suo canto del cigno, il frutto delle sue meditazioni, che avevano spaziato dalla matematica pura alla fisica teorica, dalla filosofia all'arte. Ritentare a distanza di trent'anni un'impresa del genere sarebbe quanto meno presuntuoso e il tema deve perciò essere rigidamente confinato alle competenze dell'autore. Questo articolo perciò non tratterà che della simmetria nella fisica, dove il concetto di simmetria ha avuto, nel nostro secolo, applicazioni estremamente fruttuose. Del vastissimo sviluppo di tale concetto nella matematica, su cui le applicazioni alla fisica si fondano, tratta esaurientemente l'articolo di G. W. Mackey (v. gruppi).

La parola greca συμμετρία possedeva già il significato che oggi comunemente le attribuiamo: giusta proporzione, riduzione a una comune misura, corrispondenza, commensurabilità. Oggi diciamo che una figura, una struttura, un motivo ornamentale possiedono una simmetria se una qualche operazione spaziale, quale una traslazione, una rotazione, una riflessione rispetto a un punto, un asse, un piano, lascia invariate le relazioni reciproche fra gli elementi della struttura. Sono queste relazioni invarianti che costituiscono l'essenza della figura e non la sua particolare orientazione spaziale. E. Cassirer (v., 1910), nel suo libro Substanzbegriff und Funktionsbegriff, esprime chiaramente questo concetto: ‟Consideriamo geometriche solo quelle proprietà che restano invariate sotto certe trasformazioni spaziali. [...] Il concetto di indipendenza da queste trasformazioni deve essere aggiunto alla intuizione della forma individuale, che serve come punto di partenza, per dare a questa forma vera universalità e perciò vero carattere geometrico".

Al concetto di simmetria sono connessi quelli di regolarità, uniformità, ordine, concetti questi che hanno ispirato la scienza fin dal suo nascere. Una delle prime teorie dei moti planetari fu quella di Eudosso, altamente simmetrica perché basata su un insieme di cerchi concentrici; essa nacque, come riferisce Simplicio, in risposta al quesito di Platone di quali fossero i movimenti ‛uniformi' e ‛ordinati' che i pianeti, o meglio le loro sfere, dovevano avere per dar luogo al moto apparente, la cui irregolarità violava l'ordine e la simmetria, che invece, per gli antichi filosofi, il κόσμος doveva necessariamente possedere. Troviamo qui anticipato il motivo ispiratore della fisica attraverso tutto il suo sviluppo futuro: la ricerca, cioè, dell'ordine e della simmetria delle leggi fondamentali, spesso oscurati dall'apparente irregolarità dei fenomeni. In questo senso il quesito posto da Platone resta ancora oggi profondamente attuale.

Un'applicazione più concreta dei principî di simmetria fu fatta da Archimede, che fondò la sua teoria della leva sul teorema che pesi uguali sospesi a bracci uguali devono, per la simmetria della configurazione, essere in equilibrio (v. Weyl, 1949). Anche in questo caso la scienza greca anticipava il punto di vista moderno e, a distanza di ventitré secoli, P. Curie (v., 1894) sembra riecheggiare Archimede quando formula il suo famoso principio, ‟gli elementi di simmetria delle cause devono essere presenti negli effetti che producono", che si può dire apra l'epoca moderna dell'applicazione della simmetria alla fisica.

Nel lungo lasso di tempo che intercorre fra Archimede e P. Curie la ricerca della simmetria delle leggi della natura continuò a essere uno dei Leitmotive della fisica. All'inizio dell'epoca moderna Kepler si ispira alle proprietà di simmetria dei solidi regolari per spiegare le distanze dei pianeti dal Sole. Galileo con il principio di relatività pone su basi precise lo studio della simmetria dello spazio-tempo e nei Discorsi e dimostrazioni matematiche intorno a due scienze nuove esamina la simmetria delle leggi fisiche rispetto ai cambiamenti di scala (oggi diremmo rispetto al gruppo delle dilatazioni). Newton ebbe certo presente l'importanza dell'isotropia e dell'omogeneità dello spazio per la struttura delle leggi fisiche, e poco più tardi Euler, nel De motu corporum rigidorum, mostrò con un calcolo esplicito l'invarianza delle leggi della meccanica rispetto alle trasformazioni di Galileo e affermò chiaramente che lo stato di riposo e quello di moto rettilineo uniforme sono dinamicamente indistinguibili.

Le trattazioni successive della meccanica non sembrano tuttavia seguire esplicitamente questi spunti anticipatori dei fondatori della scienza moderna: la simmetria resta fino all'inizio di questo secolo qualcosa di mezzo fra un ideale astratto e un metodo pratico per la trattazione matematica di problemi particolari (la scelta delle coordinate più adatte), ma non sembra giocare una parte preponderante nel pensiero fisico dell'Ottocento.

È con l'inizio del nostro secolo che il problema della simmetria delle leggi fisiche, e quello ad esso collegato della struttura matematica dello spazio-tempo, diviene uno dei problemi centrali della fisica. Questo nuovo atteggiamento fu sostanzialmente dovuto alla possibilità, che si presentò allora per la prima volta, di formulare in maniera precisa, nel linguaggio della teoria dei gruppi, da poco sviluppata dai matematici, il concetto di simmetria delle equazioni della fisica e di dedurne tutte le conseguenze. Weyl (v., 1949), riecheggiando F. Klein, afferma che quello di gruppo è stato probabilmente il concetto più caratteristico della matematica del XIX secolo. ‟La definizione stessa di gruppo - dice Cassirer nel libro già citato - contiene un nuovo e importante aspetto logico, in quanto, per mezzo di questo concetto, si riduce ad unità matematica non tanto una collettività di elementi o strutture individuali, quanto un sistema di operazioni". L'applicazione di questo concetto alla fisica si è dimostrata di una straordinaria fertilità e ha dato luogo a una corrente di pensiero oggi ancora in pieno sviluppo. Ancora una volta si dimostrò quella che Wigner (v., 1960) ebbe a chiamare la ingiustificabile (unreasonable) applicabilità della matematica alla fisica, di un tipo di matematica, anzi, che gli stessi matematici consideravano all'inizio troppo astratta per trovare applicazioni nella fisica.

Nel linguaggio della teoria dei gruppi possiamo oggi dare una definizione di simmetria assai più precisa e generale della nozione comune strettamente legata a un'immagine geometrica: un insieme è simmetrico se le relazioni fra i suoi elementi sono invarianti rispetto a un gruppo di trasformazioni dei suoi elementi. Questa definizione non richiede in alcun modo che gli elementi dell'insieme abbiano un'interpretazione geometrica, né che le trasformazioni del gruppo siano rappresentabili come operazioni spaziali. Potremo per esempio dire che un sistema di equazioni possiede una certa simmetria se mantiene la stessa forma quando le grandezze che vi compaiono sono assoggettate alle trasformazioni di un gruppo. Così la celebre equazione della dinamica, F=ma, che esprime la proporzionalità fra la forza agente su un punto di massa m e l'accelerazione che questo subisce, è invariante rispetto alle trasformazioni del gruppo di Galileo generato dalle rotazioni spaziali, dalle trasformazioni a sistemi di riferimento in moto rettilineo uniforme e dalle traslazioni delle origini dei riferimenti spaziali e temporali.

Simmetria e invarianza rispetto a un gruppo di trasformazioni diventano dunque sinonimi e di simmetria si può quindi parlare in un senso assai più lato di quello comunemente attribuitole, anche quando gli elementi cui la si applica non hanno alcuna rappresentazione concreta.

La prima e più ovvia applicazione della teoria dei gruppi alla fisica fu la classificazione dei cristalli secondo le proprietà dei gruppi spaziali ad essi associati (v. gruppi). La simmetria dei cristalli era naturalmente ben nota ai cristallografi dell'Ottocento, ma solo lo studio delle proprietà dei gruppi discreti permise di elencare tutti i possibili gruppi di invarianza dei reticoli cristallini, reticoli che di là a poco divennero ‛visibili', grazie alla diffusione di raggi X e, più tardi, di elettroni.

Fu però la teoria dei gruppi continui di trasformazioni, iniziata da S. Lie intorno al 1870, quella che si dimostrò più fruttuosa nelle sue applicazioni alla fisica. Essa condusse in maniera naturale a definire il concetto di simmetria o invarianza delle leggi fisiche rispetto a un gruppo continuo di trasformazioni, concetto che rappresenta una delle innovazioni più significative della fisica del nostro secolo. Pur non essendosi occupato delle applicazioni alla fisica, Lie affermò tuttavia esplicitamente (prefazione alla parte III dell'opera Transformationsgruppen, p. VII): ‟I principî della meccanica hanno un'origine gruppale", origine che più tardi fu dimostrata da G. Hamel (v., 1904). Continuando questa linea di pensiero, Engel mostrò (v., 1916) la connessione fra il gruppo di invarianza della meccanica classica e le leggi di conservazione della quantità di moto, del momento angolare e della velocità del baricentro; poco più tardi, nel 1918, E. Noether generalizzò questo risultato a tutti i gruppi continui finiti e infiniti. Queste ricerche estendevano alla meccanica galileiana e relativistica il punto di vista già applicato con tanto successo alla geometria da Klein, che, nel suo famoso Erlangen Programm (1872), aveva affermato che una geometria è definita da un gruppo di trasformazioni ed è lo studio di quanto resta invariante rispetto ad esse.

Si apriva così quella che possiamo chiamare l'epoca moderna dell'applicazione della simmetria alla fisica, così ben caratterizzata da Weyl nel suo già citato Symmetry: ‟Condividiamo ancor oggi la sua [di Kepler] fede nell'armonia matematica dell'universo: essa ha retto all'esame di un'esperienza sempre più vasta. Oggi però non ricerchiamo più quest'armonia in forme statiche come i solidi regolari, ma in leggi dinamiche". Il concetto di simmetria ha assunto nella fisica di oggi un significato assai più astratto di quello comunemente usato e si riferisce alla simmetria delle leggi della natura rispetto a gruppi di trasformazioni non necessariamente agenti sullo spazio-tempo. Mentre le leggi fisiche esprimono relazioni a cui gli eventi fisici devono soddisfare, i principi di simmetria rappresentano condizioni imposte alle leggi stesse, condizioni che spesso consentono, anche se la forma esplicita delle leggi ci è ignota, di trarre conseguenze osservabili.

Lo scienziato che più di ogni altro comprese le conseguenze della simmetria delle leggi fisiche, mettendone in luce le profonde e rivoluzionarie implicazioni, fu certamente Einstein, con le due teorie della relatività speciale e di quella generale. Invero, come subito osservò Klein (v., 1910), relatività significa invarianza rispetto a un gruppo di trasformazioni e implica perciò una particolare simmetria delle equazioni della teoria, a sua volta riflesso della geometria postulata per l'insieme degli eventi fisici, cioè per lo spazio-tempo.

La teoria della relatività speciale ricevette prestissimo ampie conferme sperimentali e divenne così quasi subito parte integrante della fisica. La relatività generale, invece, la cui struttura gruppale è assai più complessa, rimase per lungo tempo un po' al di fuori della corrente principale della fisica del nostro secolo. Ciò fu dovuto in parte alla difficoltà di sottoporla a verifiche sperimentali stringenti e in parte al fatto che essa riguardava esclusivamente le interazioni gravitazionali e non sembrava possibile estenderla, nonostante gli sforzi dello stesso Einstein e di numerosi altri studiosi, alle altre interazioni. Oggi, a distanza di sessantacinque anni, siamo in grado di riconoscerne il carattere profondamente anticipatore e cominciamo a intravedere la possibilità di far discendere le caratteristiche di tutte le interazioni fondamentali dalle proprietà geometriche dello spazio (inteso in un significato esteso) ossia dalle sue proprietà di simmetria. È questo il programma ambizioso delle teorie di gauge non abeliane.

L'applicazione della teoria dei gruppi alla fisica iniziata da Einstein trovò il suo terreno più fertile nella meccanica quantistica, la cui struttura matematica particolarmente semplice permetteva di usare la teoria della rappresentazione lineare dei gruppi. Grazie all'opera di Weyl (v., 1928) e di Wigner (v., 1931), fu possibile, già alla fine degli anni venti, dare un'interpretazione relativamente semplice della struttura degli spettri atomici, tanto che M. von Laue poteva affermare che praticamente tutte le regole della spettroscopia seguono dalla simmetria del problema.

Gli stessi metodi applicati con tanto successo alla fisica atomica furono più tardi estesi dallo stesso Wigner, e, successivamente, da numerosi altri studiosi, alle molecole e ai solidi e poco più tardi ai nuclei, dimostrandosi, anche in questi casi, estremamente fruttuosi. Nel caso dei nuclei la situazione era alquanto diversa da quella della fisica atomica: mentre in quest'ultimo caso le forze, cioè quelle elettromagnetiche, erano ben note e le loro proprietà di simmetria rispetto alle rotazioni spaziali e alle permutazioni degli elettroni erano esatte, le forze nucleari erano invece mal note e la loro invarianza rispetto alle trasformazioni delle variabili interne era soltanto approssimata. Ciononostante i metodi della teoria dei gruppi si dimostrarono enormemente fecondi e permisero anche di comprendere, almeno fenomenologicamente, le proprietà delle varie particelle elementari che si andavano man mano scoprendo.

Verso la fine degli anni cinquanta, la scoperta della violazione della simmetria rispetto alle riflessioni spaziali e alla coniugazione di carica, nelle interazioni deboli, e di quella di numerose simmetrie interne approssimate valide solo per le interazioni forti contribuirono a mettere a fuoco l'importanza del fenomeno della rottura spontanea della simmetria. Questo fenomeno, già noto nell'ambito della fisica classica (si pensi alle transizioni di fase, ai cambiamenti di regime in idrodinamica o, più in generale, alla infinita varietà delle forme di aggregazione della materia), richiede che si spieghi come equazioni dotate di simmetria possano dar luogo, senza l'intervento di cause asimmetriche, a soluzioni stabili, o metastabili, asimmetriche. Lo studio dell'origine dell'asimmetria degli stati fisici da forze elementari simmetriche è uno dei campi di ricerca oggi più attivi. Ha implicazioni profonde in fenomeni diversissimi, come l'origine di correnti convettive nell'atmosfera terrestre e in quelle stellari; l'origine della dinamo magnetica, sorgente del campo magnetico terrestre e di quelli stellari; l'origine delle forme nelle strutture dissipative, come quelle biologiche o quelle astronomiche; e infine l'origine delle interazioni asimmetriche, osservate nelle condizioni fisiche attuali, da un'interazione unica altamente simmetrica che dominava nei primissimi istanti della formazione del cosmo. Il secolo che si era aperto con la scoperta delle profonde implicazioni della simmetria delle leggi fisiche affronta così al suo declino il problema di riconciliare tale simmetria con la sua violazione, senza la quale il cosmo si ridurrebbe all'informe caos. Va infatti notato che l'ordine e l'armonia del cosmo ci si rivelano proprio attraverso il riconoscimento di forme e strutture che rappresentano scelte definite fra l'infinità informe di possibilità che la simmetria originaria permetterebbe. La fisica moderna ci riporta dunque in forma più precisa al problema originario di come dall'osservazione di fenomeni asimmetrici si possa risalire alle loro più simmetriche cause.

2. La struttura dello spazio-tempo assoluto.

Tutta la fisica precedente la relatività generale è fondata sul postulato che l'insieme degli eventi fisici sia isomorfo a uno spazio affine a quattro dimensioni ???OUT-R???⁴ dotato di coordinate {t, x=(x₁, x₂, x₃)} che rappresentano il tempo e la posizione dell'evento. Questa struttura è data a priori, indipendentemente dalla presenza di materia e dall'esistenza di campi di forze: essa è la sede dei fenomeni fisici che ne lasciano invariate le proprietà geometriche. Le leggi che governano i fenomeni sono relazioni fra eventi (cioè fra gli elementi dello spazio-tempo), espresse normalmente come equazioni differenziali la cui forma è suggerita dall'esperienza.

Questa concezione dello spazio-tempo è comune alla fisica newtoniana e a quella della relatività speciale di Einstein, le quali tuttavia differiscono per la diversa topologia che presuppongono per ???OUT-R???⁴. Per determinare la geometria dello spazio-tempo (la parola geometria è qui usata nel senso astratto di Klein), occorre determinare quale sia il gruppo degli automorfismi di ???OUT-R???⁴, cioè il gruppo delle applicazioni lineari ???OUT-R???⁴→???OUT-R???⁴ che lasciano invariate le relazioni oggettive fra gli elementi dello spazio, ossia le leggi fisiche. Chiameremo tale gruppo il gruppo di simmetria dello spazio-tempo. È sulla oggettività delle leggi che la fisica newtoniana e quella della relatività einsteiniana differiscono. Per ambedue lo stato di quiete e quello di moto rettilineo uniforme (e solo questo) non sono oggettivamente distinguibili; ma, mentre la fisica newtoniana ammette che la contemporaneità fra due eventi in posizioni diverse sia una relazione oggettiva, quest'ipotesi non è più richiesta dalla relatività speciale. La possibilità di definire in maniera oggettiva la contemporaneità di due eventi spazialmente distinti riposa sull'ammissione che si possa disporre, per sincronizzare gli orologi, di segnali con velocità infinita, ipotesi che Einstein lasciò cadere in favore di quella che la luce fornisca il segnale più veloce.

È facile convincersi che il gruppo di simmetria dello spazio-tempo compatibile con la fisica newtoniana è un gruppo di Lie non compatto a 10 parametri, chiamato gruppo di Galileo, che indicheremo con G_∞, i cui elementi (τ, a, v, R) agiscono su ???OUT-R???⁴ nella maniera seguente:

(τ, a, v, R):(t, x)???14???(t+τ, a+vt+Rx). (1)

Questa azione rappresenta una traslazione temporale τ, una traslazione spaziale a, una trasformazione a un sistema in moto con velocità uniforme v e una rotazione spaziale rappresentata da una matrice 3×3 ortogonale (RR^t=1).

Il gruppo di Galileo G_∞ è il prodotto semidiretto del gruppo abeliano delle traslazioni spazio-temporali {(τ, a, 0, 1)} (1 è la matrice unità 3×3) e di un gruppo a 6 dimensioni {(0, 0, v, R)}, il quale, a sua volta, è il prodotto semidiretto di un gruppo di traslazioni a 3 dimensioni {(0, 0, v, 1)} e del gruppo delle rotazioni spaziali SO(3)={(0, 0, 0, R)}. I generatori infinitesimi E, P=(P₁, P₂, P₃), K=(K₁, K₂, K₃), L=(L₁, L₂, L₃) delle trasformazioni associate rispettivamente ai parametri τ, a, v, R costituiscono una base dell'algebra di Lie del gruppo G_∞ con prodotti anti simmetrici:

dove ε_ijk è il tensore isotropo antisimmetrico in 3 dimensioni.

Come si verifica facilmente, ogni trasformazione del gruppo G_∞ lascia invariati separatamente l'intervallo di tempo t′−t e il quadrato della distanza spaziale ∥x′−x∥² fra due eventi con coordinate temporali t e t′ e coordinate spaziali x e x′. La struttura dello spazio-tempo che deriva da questo gruppo di invarianza è quella di un fibrato ???OUT-R???⁴=(???OUT-R???, ???OUT-R???³, π) con base ???OUT-R??? (il tempo), fibra ???OUT-R???³ (lo spazio) e proiezione π sulla base data dalla convenzione per sincronizzare gli orologi. Come ha fatto osservare Weyl, questa struttura, in cui il tempo e lo spazio hanno un ruolo profondamente asimmetrico, è determinata dal gruppo G_∞ nello stesso modo in cui l'invarianza rispetto al gruppo euclideo E₃={a, R}, generato dalle traslazioni e dalle rotazioni, determina la geometria euclidea nello spazio ordinario.

La geometria galileiana dello spazio-tempo, per quanto in accordo con l'imponente massa di dati astronomici accumulati durante il XVIII e il XIX secolo, si dimostrò inadatta a rendere conto dei fenomeni elettromagnetici. Le equazioni di Maxwell, che contengono come parametro la velocità della luce c, non sono infatti invarianti rispetto a G_∞, che non può pertanto essere considerato il gruppo di simmetria dello spazio-tempo. Il gruppo di invarianza delle equazioni di Maxwell è un gruppo di Lie non compatto a dieci parametri, G_c, chiamato gruppo di Poincaré (o gruppo di Lorentz non omogeneo), i cui elementi sono gli automorfismi di ???OUT-R???⁴ che lasciano invariato il quadrato della ‛distanza' fra due eventi di coordinate x=(ct, x) e x′(ct′, x′), cioè la forma quadratica

(ct−ct′)²−∥x−x′∥²=(x−x′∣η(x−x′)). (2)

In questa relazione, η è la matrice diagonale 4×4 con elementi (1, −1, −1, −1) (tensore di Minkowski) e c è la velocità della luce. Gli elementi (a, Λ) e G_c dipendono da un vettore quadridimensionale a=(cτ, a) e da una matrice Λ, 4×4, dipendente da una matrice ortogonale R, 3×3, e da un trivettore v che soddisfa la relazione Λ^tηΛ=η. La loro azione su ???OUT-R???⁴ è

(a, Λ):x???14???a+Λx, x∈???OUT-R???⁴. (3)

L'insieme delle matrici Λ è il gruppo di Lie a sei parametri SO(3, 1) che prende anche il nome di gruppo di Lorentz omogeneo.

Le matrici Λ dipendono da c e la loro forma è tale che nel limite c→∞ la (3) si riduce alla (1). Il gruppo G_∞ appare perciò come un caso particolare e matematicamente meno elegante di G_c, il quale contrae (con la definizione di Wigner e Inonu) a G_∞ per c→∞. Einstein fu il primo a riconoscere che il gruppo G_c, già discusso da Poincaré, è il vero gruppo di invarianza dello spazio-tempo. Soltanto perché nella maggior parte dei fenomeni meccanici intervengono velocità molto minori di quella della luce l'azione del gruppo di Poincaré può essere approssimata con quella del gruppo di Galileo. Le basi dell'algebra di Lie del gruppo di Poincaré

hanno i seguenti prodotti antisimmetrici:

Solo i due ultimi prodotti differiscono da quelli dell'algebra di Lie del gruppo di Galileo e a questi si riducono nel limite c→∞.

Nel suo celebre discorso di Colonia, nel 1908, Minkowski osservò che il carattere di generalità e di eleganza di G_c avrebbe dovuto essere sufficiente a suggerire ai matematici di basare su di esso, anziché su G_∞, la geometria dello spazio-tempo. Se la cosa non avvenne e toccò a un fisico scoprire il vero gruppo di simmetria dello spazio-tempo, ciò è probabilmente dovuto alla scarsa importanza attribuita fino a quel tempo alla teoria dei gruppi come strumento di indagine fisica.

Come è ben noto, la concezione dello spazio-tempo che discende dal gruppo G_c è radicalmente diversa da quella galileiana. Per usare le parole di Einstein (v., 1955), ‟non esiste alcuna divisione oggettiva e razionale del continuo quadridimensionale in uno spazio tridimensionale e in un continuo unidimensionale", ossia, in linguaggio meno tecnico, e sono ancora parole di Einstein, ‟non vi è alcuna relazione spaziale o temporale assoluta (cioè indipendente dal sistema di riferimento) fra due eventi". La geometria galileiana si presenta come un'approssimazione, ben soddisfatta per velocità molto minori di quella della luce, della geometria minkowskiana fondata sul gruppo di Poincaré G_c. In quest'ultima la struttura fibrata dello spazio-tempo galileiano è perduta per l'impossibilità di definire in maniera invariante la simultaneità di due eventi in punti diversi e l'unica traccia dell'asimmetria fra spazio e tempo è nella segnatura (1, −1, −1, −1) della matrice minkowskiana. L'isotropia e l'omogeneità dello spazio tridimensionale postulate da Newton vengono ora estese allo spazio-tempo ???OUT-R???⁴, con le cautele necessarie per tener conto della non positività della ‛distanza' (2).

In virtù del teorema di Noether, l'esistenza di un gruppo di automorfismi dello spazio-tempo, dipendente da dieci parametri, implica l'esistenza di dieci leggi di conservazione, ossia l'esistenza, per ogni sistema isolato, di dieci costanti del moto. Ciò è vero tanto per la fisica newtoniana quanto per la relatività ristretta. Le dieci grandezze sono: l'energia e l'impulso del sistema, connesse ai parametri τ e a (traslazioni temporali e spaziali), il momento angolare, connesso ai tre parametri della matrice R, conseguenza dell'invarianza rispetto alle rotazioni spaziali, e la velocità del centro di massa, connessa ai parametri v, che proviene dall'invarianza rispetto al passaggio a un sistema di riferimento in moto rettilineo uniforme. Queste leggi di conservazione erano naturalmente ben note ai fisici del XIX secolo, ma soltanto l'applicazione sistematica dei concetti gruppali ha mostrato che esse riflettono unicamente le proprietà di simmetria dello spazio-tempo. Questo risultato, almeno per quanto riguarda la conservazione dell'impulso, era già noto a Newton, ma solo in questo secolo se ne è apprezzata la grande generalità.

3. Il ruolo della simmetria nella meccanica quantistica.

a) Considerazioni generali.

Il concetto di simmetria ha trovato la sua applicazione più fruttuosa nell'ambito della meccanica quantistica (v. quanti, teoria dei), sviluppata, a partire dal 1925, per interpretare i fenomeni atomici e più tardi estesa con successo a quelli nucleari e subnucleari. Come è noto (v. atomo), le righe di emissione che caratterizzano lo spettro di un atomo sono spiegabili come transizioni fra due livelli energetici dell'atomo causate dall'accoppiamento fra gli elettroni e il campo elettromagnetico. La frequenza della luce emessa in queste transizioni è proporzionale alla differenza fra le energie degli stati iniziale e finale. Però non tutte le righe che potrebbero ottenersi accoppiando fra loro tutti gli stati stazionari sono effettivamente presenti nello spettro: molte appaiono vietate da regole di selezione empiricamente dedotte dagli spettroscopisti. Si osserva inoltre che, in presenza di un campo magnetico (o elettrico), la maggior parte delle righe spettrali si scinde in diverse componenti, le cui intensità stanno fra loro in rapporti ben definiti.

Un atomo con più di un elettrone è, dal punto di vista dinamico, un sistema estremamente complicato; ciononostante i suoi livelli energetici sono definibili per mezzo di pochi numeri quantici interi o seminteri. È stato uno dei successi più significativi dell'applicazione dei concetti di simmetria alla meccanica quantistica l'aver dimostrato, come disse Weyl (v., 1928) nel suo celebre trattato Gruppentheone und Quantenmechanik, che ‟tutti i numeri quantici, ad eccezione del cosiddetto numero quantico principale, sono indici che caratterizzano le rappresentazioni di gruppi". La struttura dell'insieme degli stati atomici non dipende cioè dai dettagli della dinamica, ma solo dalle proprietà di simmetria dell'atomo stesso rispetto alle rotazioni e alle riflessioni spaziali e allo scambio degli elettroni.

Il successo dei metodi gruppali nella meccanica quantistica è dovuto alla linearità dello spazio degli stati di un sistema quantistico, la quale, a sua volta, esprime il contenuto del principio di sovrapposizione. Più precisamente (v. quanti, teoria dei: Meccanica quantistica), l'insieme ℋ degli stati di un sistema quantistico, detto spazio degli stati, ha la struttura di uno spazio di Hilbert complesso, e le grandezze osservabili, come l'energia, il momento angolare ecc., sono rappresentate da operatori autoaggiunti su ℋ, il cui spettro è l'insieme dei valori che le grandezze in questione possono assumere. L'insieme degli operatori lineari autoaggiunti su ℋ è uno spazio vettoriale, A(ℋ), detto spazio delle osservabili. Solo gli elementi di questo spazio che commutano fra loro sono simultaneamente osservabili. Un insieme di operatori autoaggiunti A₁, ..., A_n, che commutano fra loro, si dice completo se i loro autovettori simultanei A_iϕ_α1,...,_αn=α_iϕ_α1,...,_αn sono univocamente individuati dagli autovalori α₁, ..., α_n.

Consideriamo ora un gruppo G e una sua rappresentazione unitaria (v. Wigner, 1931; v. Weyl, 1928) sugli spazi ℋ e A(ℋ) di un sistema fisico, definita dall'omomorfismo U:G+U(ℋ) di G nel gruppo degli operatori unitari su ℋ che associa a ogni g∈G l'operatore unitario U_g. Un sottospazio ℋ_α⊂ℋ (o A_α(ℋ)⊂A(ℋ)) si dice G-invariante se, per ogni g∈G, Ug^(α) ℋ_α⊂ℋ_α, dove, Ug^(α) è la restrizione di U_g al sotto spazio ℋ_α. Un sottospazio G-invariante ℋ_α si dice irriducibile se non contiene alcun sottospazio G-invariante oltre a ℋ_α e al vettore nullo; la restrizione U^(α) di U al sottospazio ℋ_α è detta rappresentazione irriducibile. Sottospazi irriducibili appartenenti a rappresentazioni diverse sono ortogonali. Le rappresentazioni irriducibili dei gruppi di interesse fisico sono ormai note e classificate. Se U^(α) e U^(β₎ sono due rappresentazioni irriducibili, il loro prodotto tensoriale, cioè la rappresentazione U^(α)×U^(β):g???14???Ug^(α)×Ug^(β), non è in generale irriducibile, ma può venire decomposto nella somma diretta di rappresentazioni irriducibili: Ug^(α)×Ug^(β)=⊕_γ Ug^(γ) (per maggiori dettagli v. gruppi).

Possiamo ora dare la definizione di sistema quantistico G-invariante. Un sistema quantistico è G-invariante se tutte le sue grandezze osservabili A sono G-invarianti, cioè se, per ogni g∈G, U−_g ¹ A U_g=A. Se A₁, ..., A_n è un sistema completo di operatori autoaggiunti che commutano, in generale solo un sottoinsieme di essi, A₁, ..., A_k, k≤n, è G-invariante e solo le funzioni degli operatori di questo sottoinsieme sono effettivamente osservabili. Pertanto a un insieme α=(α₁, ..., α_k) di autovalori di A₁, ..., A_k corrispondono in genere più autovettori indipendenti, i quali generano un sottospazio ℋ_α di ℋ, che è chiamato livello o multipletto. Se le dimensioni di ℋ_α sono maggiori di uno, il livello α si dice degenere. La degenerazione dei livelli di un sistema quantistico appare dunque come una diretta conseguenza della simmetria, la quale impedisce di misurare tutti gli operatori di un sistema completo. Tale degenerazione si rimuove solo introducendo qualche effetto asimmetrico, quale un campo elettrico o magnetico, che permetta di misurare gli operatori non G-invarianti.

Oltre alla degenerazione dei livelli energetici, la G-invarianza di un sistema quantistico ha un'altra importante consegnenza sulle probabilità di transizione fra livelli diversi. Consideriamo l'elemento di matrice (ϕ_γ, A_βϕ_α) di un operatore A_β∈A_β(ℋ) fra due stati ϕ_α∈ℋ_α e ϕ_γ∈ℋ_γ. In generale lo stato A_βϕ_α non appartiene a un sottospazio irriducibile di ℋ. Solo se A_βϕ_α ha una proiezione non nulla su ℋ_γ l'elemento di matrice è diverso da zero; in caso contrario si dice che esiste una regola di selezione per la transizione da ϕ_α a ϕ_γ causata da A_β. La teoria dei gruppi permette di determinare quali spazi irriducibili compaiano nel prodotto A_β(ℋ)ℋ_α e i loro pesi relativi. Se le transizioni da ϕ_α a due stati ϕ_γ e ϕ_δ, appartenenti a sottospazi irriducibili diversi, sono ambedue permesse, è quindi anche possibile predire il valore del rapporto ∣(ϕ_γ, A_βϕ_α)∣²/∣(ϕ_δ, A_βϕ_α)∣² fra le probabilità di transizione ai due stati e il valore del rapporto fra le intensità delle righe emesse nelle transizioni ϕ_α→ϕ_γ e ϕ_α→ϕ_δ.

b) La classificazione dei livelli atomici.

Il gruppo di invarianza dell'hamiltoniana di un atomo isolato è il gruppo di Poincaré o, se si trascurano gli effetti relativistici, quello di Galileo. In generale non ci interessa però il moto dell'atomo nel suo insieme, ma solo il moto interno dei suoi N elettroni. Ci si può dunque porre nel sistema di riferimento in cui l'impulso del baricentro, che supponiamo coincida con il nucleo, è nullo e trascurare le trasformazioni a sistemi di riferimento in moto e le traslazioni spaziali, le quali, quando l'impulso è nullo, agiscono in maniera banale. Rimane pertanto il gruppo ???OUT-R???×SO(3), dove ???OUT-R??? è il gruppo abeliano delle traslazioni temporali e SO(3) quello delle rotazioni spaziali.

Accanto a questa simmetria di natura puramente geometrica, ve ne sono altre due, che discendono dalle proprietà generali della dinamica dell'atomo. Questa è governata dalle interazioni elettromagnetiche, le quali sono invarianti rispetto all'inversione delle coordinate spaziali, e cioè rispetto al gruppo Z₂, i cui elementi sono l'identità 1 e l'operatore di inversione spaziale P, P²=1, P:x???14???−x. Nel caso classico l'invarianza rispetto a Z₂ non dà luogo ad alcun effetto osservabile, mentre, come vedremo, nel caso quantistico essa è responsabile di un'importante regola di selezione. Inoltre gli elettroni dell'atomo sono indistinguibili fra loro, caratteristica questa senza analogo classico. Ogni osservabile deve perciò essere invariante rispetto al gruppo S_N delle permutazioni degli N elettroni che compongono l'atomo. Il gruppo di simmetria di un atomo isolato con N elettroni, nel sistema in cui il nucleo è a riposo, è pertanto il prodotto diretto G=???OUT-R???×SO(3)×Z₂×S_N.

Le rappresentazioni irriducibili di G sullo spazio ℋ degli stati legati dell'atomo possono venire classificate con gli autovalori degli invarianti dei singoli gruppi. Questi invarianti sono: a) il generatore delle traslazioni temporali H, che rappresenta l'energia, i cui autovalori E〈0 caratterizzano le rappresentazioni di ???OUT-R???; b) il quadrato del momento angolare J², i cui autovalori J(J+1), dove J=0, 1, 2,... o J=1/2, 3/2,..., a seconda che N sia pari o dispari, caratterizzano le rappresentazioni irriducibili del gruppo SO(3) delle rotazioni spaziali che hanno dimensioni 2J+1; c) l'operatore di inversione spaziale P, i cui autovalori (parità) w=±1 caratterizzano le rappresentazioni di Z₂; d) i caratteri del gruppo delle permutazioni (v. gruppi), i cui autovalori determinano la simmetria dello stato rispetto alle permutazioni degli elettroni. Il principio di esclusione di Pauli (v. oltre) richiede che, fra tutte le rappresentazioni di S_N sullo spazio degli stati di N elettroni, solo quella antisimmetrica si realizzi in natura. Questa condizione, come vedremo nel È c, permette di spiegare le proprietà chimiche degli atomi.

Ciascun livello atomico antisimmetrico rispetto a S_N può dunque venire classificato con i tre numeri quantici (E, J, w). Nel punto seguente vedremo come a questi è possibile aggiungerne altri legati a simmetrie approssimate.

La simmetria di scambio delle coordinate di spin. - Gli elettroni possiedono, oltre alla carica e alla massa, anche un momento angolare intrinseco di spin s=1/2 (v. oltre), in unità ℏ, la cui componente lungo un asse può assumere due valori, m_s=±1/2. Scambiare due elettroni significa scambiare non solo le loro coordinate spaziali, ma anche le loro variabili di spin m_s. Per il principio di esclusione, solo stati antisimmetrici nello scambio simultaneo di tutte queste variabili sono permessi.

Nel caso dell'elio, che ha due soli elettroni, l'insieme di questi stati antisimmetrici si divide, se si trascurano correzioni relativistiche, in due sottoinsiemi distinti: a) stati simmetrici rispetto allo scambio delle coordinate spaziali e perciò antisimmetrici rispetto a quelle di spin (stati del paraelio); b) stati antisimmetrici rispetto allo scambio delle variabili spaziali e perciò simmetrici rispetto a quelle di spin (stati dell'ortoelio).

Weyl (1925) ha mostrato che esiste una corrispondenza biunivoca fra le rappresentazioni irriducibili del gruppo delle permutazioni S_N sullo spazio a 2N dimensioni delle variabili di spin di N elettroni e quelle del gruppo U(2) delle trasformazioni unitarie in due dimensioni. Queste ultime sono individuate da N e dagli autovalori dell'operatore

dove gli operatori s_i, [s_i, s_j]=is_k, s²_i=1/4 sono una base dell'algebra degli operatori lineari sullo spazio a due dimensioni generato dai vettori χ_ms, m_s±1/2, tali che s₃χ_ms=m_sχ_ms. Dalle regole di commutazione degli operatori s_i segue che gli autovalori di S² sono S(S+1), dove S, che è chiamato spin totale, può assumere i valori S=N/2, N/2−1, N/2−2,... fino a zero o 1/2, a seconda che N sia pari o dispari. È facile verificare che, nel caso di due elettroni, gli stati del paraelio, antisimmetrici rispetto alle variabili m_s dei due elettroni, sono stati con S=0, quelli simmetrici dell'ortoelio sono invece stati con S=1.

La simmetria rispetto allo scambio degli elettroni è perciò responsabile della separazione dei livelli dell'atomo di elio in due serie distinte, con S=0 e S=1, fra le quali, come vedremo, non possono aversi transizioni (v. fig. 1). Questo risultato di fondamentale importanza, che non aveva alcuna interpretazione nella meccanica classica, è stato ottenuto da Heisenberg (v., 1926).

Poco dopo, Wigner (v., 1927) dimostrò che le considerazioni di Heisenberg sulle conseguenze della simmetria di scambio potevano venire estese con buona approssimazione ad atomi con un numero qualsiasi di elettroni. Si poteva cioè ammettere che il gruppo SO(3)×Z₂×S*_N, dove S*_N è il gruppo delle permutazioni delle sole variabili di spin, fosse una simmetria approssimata dell'atomo, utilizzabile per classificare i livelli energetici. Le rappresentazioni irriducibili di tale gruppo sono caratterizzate dagli autovalori di quattro operatori: a) S², definito nella (5), con autovalori S(S+1), S=N/2, N/2−1,...; b) L², con autovalori L(L+1), dove L=0, 1,... è chiamato momento angolare orbitale; c) J², con autovalori J(J+1), dove J=∣L+S∣, ∣L+S−1∣,..., ∣L−S∣ è chiamato momento angolare totale; d) P, con autovalori w=±1.

Va sottolineato che S*_N non è una simmetria esatta dell'atomo: essa è violata quando cade in difetto la possibilità di separare lo scambio delle coordinate spaziali da quello delle coordinate di spin, ciò che avviene negli atomi con molti elettroni, dove gli effetti relativistici non sono più trascurabili. In questo caso né L né S sono più numeri quantici ‛buoni'. Tuttavia, in molti casi, la classificazione dei livelli basata sul gruppo di simmetria SO(3)×Z₂×S*_N è in buon accordo con quella empiricamente introdotta dagli spettroscopisti. Con ipotesi plausibili sull'energia di interazione fra il momento angolare orbitale L e quello di spin S si può calcolare la separazione fra i livelli J=∣L+S∣, ..., ∣L−S∣ (formula di Landé) e anche questa è in buon accordo con le osservazioni. (Per ulteriori dettagli v. gruppi).

Le regole di selezione. - Una delle conferme più significative della validità della classificazione dei livelli esposta più sopra è data dal confronto fra le regole di selezione che discendono dalle simmetrie esatte o approssimate e quelle osservate sperimentalmente (v. Wigner, 1931). Consideriamo una riga spettrale dovuta alla transizione fra due stati ϕ₁, ϕ₂ appartenenti a due sottospazi ℋ₁ e ℋ₂, dove gli indici 1 e 2 stanno per (E₁J₁w₁L₁S₁), (E₂J₂w₂L₂S₂). La conservazione dell'energia richiede che la frequenza ω della riga emessa sia proporzionale alla differenza di energia (E₂−E₁) dei due stati; l'intensità della riga stessa è, secondo i principi della meccanica quantistica, proporzionale al quadrato dell'elemento di matrice fra ϕ₁ e ϕ₂ dell'operatore H′=∫ d³xj(x, t)•A(x, t), che rappresenta l'energia di interazione fra la densità di corrente j(x, t), dovuta agli elettroni dell'atomo, e il potenziale vettore A(x, t) del campo elettromagnetico. Nella maggior parte delle transizioni atomiche la lunghezza d'onda della luce emessa è molto maggiore delle dimensioni atomiche. In questo caso si dimostra che l'elemento di matrice (ϕ₂, H′ϕ₁) è approssimativamente proporzionale a (E₂−E₁)(ϕ₂, D•eϕ₁), dove e è il vettore di polarizzazione della luce emessa e D è l'operatore di dipolo elettrico della distribuzione di carica. Il problema di spiegare le regole di selezione per le transizioni atomiche si riduce pertanto a quello di determinare sotto quali condizioni l'elemento di matrice (ϕ₂, D ϕ₁) si annulli. Per questo basta esaminare il comportamento dell'operatore di dipolo rispetto ai gruppi di invarianza discussi più sopra.

Poiché l'operatore di dipolo elettrico D cambia segno per inversione spaziale, P:D???14???−D, le transizioni di dipolo elettrico sono vietate fra stati appartenenti a sottospazi caratterizzati dallo stesso autovalore di P, cioè con la stessa parità w. È questa la celebre regola di selezione di O. Laporte, la cui giustificazione Wigner considerava come uno dei risultati più importanti dell'applicazione della teoria dei gruppi alla meccanica quantistica. (Notiamo di passaggio come le transizioni fra stati diversi causate da operatori con parità definita permettano di determinare soltanto le parità relative di due stati, mentre le parità assolute dei singoli stati non sono invece definibili). Inoltre, poiché D non dipende dalle variabili di spin, il suo elemento di matrice si annulla se ϕ₂ e ϕ₁ appartengono a sottospazi con S diversi. Questo spiega, in particolare, l'assenza, già segnalata, di transizioni di dipolo elettrico fra gli stati dell'ortoelio (S=1) e quelli del paraelio (S=0). Infine si può dimostrare che lo stato D ϕ₁ ha componenti non nulle solo nei sottospazi con momento angolare totale J₂=J₁ o J₂=J₁±1. Possiamo dunque concludere che le regole di selezione valide per le transizioni di dipolo elettrico, e cioè w₂=−w₁, J₂−J₁=0, ±1, L₂−L₁=0, ±1, S₂−S₁=0, sono una diretta conseguenza dell'invarianza dell'hamiltoniana (non relativistica) rispetto al gruppo SO(3)×Z₂×S*_N e non dipendono dai dettagli della dinamica.

c) L'invarianza relativistica e lo spin.

La coordinata di spin dell'elettrone m_s=±1/2 era stata introdotta ad hoc su basi puramente fenomenologiche da W. Pauli (v., Über den Einfluss..., 1925), per spiegare l'effetto Zeeman anomalo (v. atomo) e i due valori del momento angolare totale J che si presentano, per ogni valore di L±0, negli spettri dei metalli alcalini. Poco dopo, Pauli stesso (v., Über den Zusammenhang..., 1925) aveva mostrato che, se all'esistenza di questo nuovo grado di libertà ‛interno' si aggiungeva il postulato che non più di un elettrone potesse occupare lo stesso stato quantico (principio di esclusione o di Pauli), si otteneva una spiegazione di tutte le periodicità della tabella degli elementi di Mendeleev e in particolare dell'esistenza di gusci chiusi con 2, 8, 18, 32,... elettroni. Come abbiamo già visto, si giustificava pure la mancanza di stati con S=1 per due elettroni con momento orbitale nullo e le particolarità dello spettro dell'atomo di elio. Poco dopo, E. Fermi (v., 1926), P. A. M. Dirac (v., 1926) e Pauli (v., 1927) mostrarono che la termodinamica statistica di particelle che obbediscono al principio di esclusione è assai diversa da quella di Bose-Einstein valida per i fotoni e in genere per particelle di spin intero. Questa nuova statistica, detta di Fermi-Dirac, che permette solo l'esistenza di stati antisimmetrici nello scambio di due elettroni, è in accordo con i risultati sperimentali sui calori specifici e si riduce, come quella di Bose-Einstein, a quella di Boltzmann nel limite classico.

Alla coordinata di spin m_s, introdotta su base empirica da Pauli, fu attribuito, da R. L. de Kronig (v. van der Waerden, 1960) e, poco dopo, indipendentemente, da G. E. Uhlenbeck e S. Goudsmit (v., 1925), il significato di momento angolare intrinseco (spin) dell'elettrone. Tuttavia sia l'origine dello spin sia la condizione che gli stati di N elettroni dovessero appartenere alla rappresentazione antisimmetrica di S_N restavano misteriose e ingiustificate.

È stato uno dei trionfi dell'applicazione dei principî di simmetria l'aver mostrato come lo spin dell'elettrone sia una naturale conseguenza della richiesta che l'equazione quantistica dell'elettrone sia invariante rispetto alle trasformazioni del gruppo di Poincaré. Fu Dirac (v., 1928) che per primo dimostrò che lo spin 1/2 dell'elettrone è automaticamente contenuto in un'equazione per la funzione d'onda che è del primo ordine nella derivata temporale, come l'equazione di Schrödinger, ma, a differenza di questa, per soddisfare l'invarianza di Poincaré, contiene solo derivate spaziali del primo ordine.

Più tardi Wigner (v., 1939) si pose il problema di classificare tutte le rappresentazioni unitarie continue irriducibili del gruppo di Poincaré sullo spazio di Hilbert degli stati di una particella libera. Il problema è complicato per il fatto che il gruppo di Poincaré non è compatto e le sue rappresentazioni unitarie irriducibili hanno dimensioni infinite. Wigner mostrò che fra gli invarianti che classificano le rappresentazioni ve ne è uno, S², che è naturale interpretare come quadrato dello spin della particella, i cui autovalori sono S(S+1), dove S=0, 1/2, 1, 3/2,... .

Questa classificazione non predice che l'elettrone debba necessariamente appartenere alla rappresentazione S=1/2. Tuttavia Pauli (v., 1940), utilizzando risultati precedenti di M. Fierz (v., 1939), riuscì a dimostrare che una teoria relativistica di particelle libere con spin intero (S=0, 1, 2,...) non è compatibile con l'ipotesi che esse soddisfino il principio di esclusione, mentre per particelle con spin semintero (S=1/2, 3/2,...) solo il principio di esclusione permette di garantire la positività dell'energia. Questo risultato, di cui più tardi G. Lüders e B. Zumino (v., 1958) e N. Bourgoyne (v., 1958) diedero una nuova dimostrazione sotto ipotesi più generali, è il famoso teorema spin-statistica, che afferma che particelle con spin semintero seguono la statistica di Fermi-Dirac, quelle con spin intero quella di Bose-Einstein. Dal fatto che gli elettroni soddisfino la statistica di Fermi-Dirac (da questo dipende la stabilità della materia) segue dunque che il loro spin deve essere semintero: S=1/2 è la soluzione più semplice.

La richiesta che la teoria dell'elettrone sia in accordo con i principi della relatività speciale, ossia con le proprietà di simmetria dello spazio-tempo, ha dunque permesso di dimostrare come due proprietà così fondamentali delle particelle elementari e dei loro composti, cioè lo spin e la statistica, siano intimamente connesse; nel caso particolare dell'elettrone, questo permette di spiegare tutte le proprietà chimiche degli atomi e in generale le proprietà della materia condensata. Dal comportamento delle particelle con spin 1/2 alle basse temperature discendono anche le proprietà delle stelle degeneri come le nane bianche e le stelle neutroniche.

d) La coniugazione di carica, l'inversione temporale, il teorema PCT.

La teoria relativistica degli elettroni e della loro interazione con il campo elettromagnetico, cioè l'elettrodinamica quantistica (v. quanti, teoria dei: Elettrodinamica quantistica) possiede, accanto all'invarianza relativistica e a quella per riflessioni spaziali, una nuova simmetria, detta coniugazione di carica, che non corrisponde ad alcuna trasformazione dello spazio-tempo, ma esprime l'invarianza della teoria rispetto a un gruppo Z₂={1, C}, che commuta con il gruppo di Poincaré. L'operatore unitario di coniugazione C assegna a ogni stato con carica q uno stato con le stesse proprietà rispetto alle trasformazioni dello spazio-tempo, ma con carica −q. Questa proprietà di simmetria condusse Dirac (v., 1930) a suggerire l'esistenza di particelle positive coniugate dell'elettrone, identificate poi con i positroni, scoperti da Anderson nei raggi cosmici, che differiscono dall'elettrone solo per il segno della carica e del momento magnetico. Oggi si sa che l'invarianza rispetto alla coniugazione di carica si estende anche alle interazioni forti ed è così possibile associare a ogni particella un'antiparticella con la stessa massa, lo stesso spin e la stessa parità, ma con carica, numero barionico, momento magnetico ecc., opposti. La maggior parte delle antiparticelle associate alle particelle elementari oggi conosciute sono state sperimentalmente osservate.

Occorre distinguere bene fra la simmetria delle leggi e quella degli stati effettivamente realizzati in natura. Il mondo in cui viviamo non è simmetrico rispetto alla coniugazione di carica: i protoni (massicci) sono positivi e gli elettroni (leggeri) sono negativi. Tuttavia la teoria delle interazioni fra particelle cariche è completamente simmetrica rispetto allo scambio di protoni con antiprotoni e di elettroni con positroni (su questo problema v. cap. 6).

Particelle con carica nulla possono essere autoconiugate, cioè possono essere autostati di C con autovalori ±1: in questo caso particella e antiparticella coincidono. Per esempio, dal fatto che l'interazione fra il campo elettromagnetico e la densità di corrente (che cambia segno sotto C) sia invariante per coniugazione di carica si deduce che il fotone è uno stato autoconiugato con autovalore −1. Da questo segue, per esempio, che lo stato fondamentale del positronio (sistema legato costituito da un elettrone e da un positrone) e quello del mesone π⁰, i quali entrambi decadono in due fotoni, sono autostati di C con autovalore +1.

L'elettrodinamica quantistica (come del resto la meccanica classica) è invariante anche rispetto all'inversione del tempo, T:t???14???−t, x???14???x. Questa operazione è rappresentata sullo spazio di Hilbert da un operatore antiunitario V, cioè tale da trasformare il prodotto scalare di due vettori ϕ, ψ nel complesso coniugato (Vϕ, Vψ)=(-ϕ-,-ψ). Wigner (v., 1932) ha dimostrato che l'invarianza rispetto a T non conduce ad alcuna degenerazione se vi è simmetria rispetto alle rotazioni spaziali, mentre, se tale simmetria è violata, si ottiene, per sistemi con spin semintero, uno sdoppiamento dei livelli (degenerazione di Kramers) che dà luogo a effetti osservabili, per esempio nei cristalli con bassa simmetria.

L'invarianza rispetto alla coniugazione di carica C e alle riflessioni spaziali non è valida per tutte le interazioni fondamentali. Le interazioni deboli, responsabili fra l'altro dei decadimenti β dei nuclei, violano sia C che P (v. Lee e Yang, 1956), come è stato confermato misurando grandezze che cambiano segno rispetto a queste operazioni, quale, per esempio, il prodotto scalare s•p di un momento angolare e di un impulso. Le interazioni deboli sono tuttavia invarianti rispetto al prodotto CP, che è però a sua volta violato per lo meno in un altro fenomeno, il decadimento in due pioni della particella K0₂. È possibile però dimostrare che il prodotto PCT delle tre operazioni discrete di inversione spaziale, coniugazione di carica e inversione temporale, rappresentato sullo spazio di Hilbert da un operatore antiunitario θ, è una simmetria di ogni teoria di campo locale, invariante rispetto al gruppo di Lorentz proprio, nella quale gli operatori dei campi soddisfino alle regole di commutazione normali (teorema PCT; v. Pauli, 1955).

4. Fisica e geometria: la concezione riemanniana.

La ricerca di una formulazione relativistica della gravitazione condusse Einstein ad abbandonare quella che era stata l'ipotesi fondamentale di tutta la fisica precedente, cioè l'indipendenza della geometria dello spazio-tempo dai fenomeni fisici che in esso avvengono. Già sessant'anni prima, Riemann, nella sua famosa tesi di abilitazione Über die Hypothesen, welche der Geometrie zu Grunde liegen (1854), aveva osservato: ‟Se lo spazio è una varietà continua, la sua struttura metrica deve essere ricercata al di fuori di esso, nelle forze di legame che su di esso agiscono". (Per le connessioni fra la geometria riemanniana e la relatività generale v. Weyl, 1921⁴).

Il programma enunciato da Riemann trovò la sua realizzazione, sia pure parziale, nella relatività generale (v. Einstein, 1916), che considerava fra gli ‛effetti' della materia solo quelli gravitazionali. Solo per questi vale il principio di equivalenza, conseguenza dell'uguaglianza fra massa inerziale e massa gravitazionale, che asserisce la possibilità di definire localmente un sistema di coordinate spazio-temporali, anzi un insieme di sistemi di coordinate, ottenuti l'uno dall'altro per trasformazioni di Lorentz, rispetto ai quali è assente ogni effetto gravitazionale. Va sottolineato che la relatività generale applica la concezione riemanniana non già al solo spazio, come Riemann pensava, ma allo spazio e al tempo contemporaneamente, poiché, come ha insegnato la relatività speciale, la distinzione fra i due è priva di significato oggettivo.

Einstein ha esplicitamente sottolineato, fin dal suo primo articolo del 1916, che alla base della relatività generale vi è un principio di invarianza. Il rinunciare all'assioma ‟continuum spatii et temporis est absolutum" è una conseguenza necessaria del postulato ‟le leggi della fisica devono essere di natura tale da valere in sistemi di riferimento in moto arbitrario" (v. Einstein, 1955) e non già solo in quelli in moto uniforme, come richiedeva la relatività speciale. Questa richiesta di invarianza rispetto ad arbitrarie trasformazioni di coordinate conduce immediatamente ad abbandonare la struttura rigida di ???OUT-R???⁴ e a considerare lo spazio come una varietà differenziabile M. Ad essa la gravitazione conferisce una struttura metrica agendo come la ‟forza di legame" di cui parlava Riemann. In parole più precise, la gravitazione definisce su M un campo tensoriale covariante g di rango due, simmetrico e non degenere (metrica pseudoriemanniana), che rappresenta la generalizzazione del potenziale gravitazionale newtoniano. Il tensore metrico g è legato alla distribuzione di energia dalle equazioni di Einstein (v. relatività), che sono un sistema di equazioni alle derivate parziali non lineari del secondo ordine, le quali generalizzano l'equazione di Poisson.

Il ruolo della simmetria nella relatività generale diviene chiaro se si assume il punto di vista di E. Cartan (v., 1946). Questo consiste nel considerare lo spazio tangente T_m(M) a ogni punto m∈M e l'insieme dei riferimenti lorentziani su di esso, cioè l'insieme delle quaterne di vettori (e₀, e₁, e₂, e₃) di T_m(M) il cui prodotto interno è (e_α, e_β)= η_αβ, dove η è il tensore diagonale di Minkowski (1, −1, −1, −1). L'insieme di questi riferimenti nel punto m è in corrispondenza biunivoca con il gruppo di Lorentz omogeneo ℒ=SO(3, 1) e può perciò venir denotato con ℒ(M)_m. L'unione delle fibre ℒ(M)_m è il fibrato dei riferimenti lorentziani (inerziali) ℒ(M)=⋃_m∈Mℒ(M)_m di cui M è la base e SO(3, 1) il gruppo di struttura (v. geometria differenziale). Esso è l'ambiente proprio della relatività generale, dove si realizza, rispettando l'invarianza locale per le trasformazioni di Lorentz, la concezione riemanniana di una descrizione puramente geometrica della gravitazione.

Una connessione riemanniana su ℒ(M) induce su M una connessione di Levi-Civita ω (v. geometria differenziale), cioè una matrice 4×4 di 1-forme su M che definiscono la derivata esterna dei riferimenti lorentziani (e⁰, e¹, e², e³) sullo spazio duale di T_m(M):

La connessione ω è legata da una relazione non lineare (seconda equazione di struttura di Cartan) alla 2-forma di curvatura della varietà R,

R=dω+ω⋀ω, (8)

che soddisfa alle identità di Bianchi

dR+ω⋀R−R⋀ω=0. (9)

Sia ω che R hanno, accanto al loro significato geometrico, una immediata interpretazione fisica: la prima rappresenta le forze apparenti, mentre la seconda è legata alle forze di marea. Come vuole il principio di equivalenza, le forze apparenti possono essere eliminate localmente con una scelta opportuna della base su T_m(M). In effetti, per l'invarianza locale di Lorentz, la base (e⁰, e¹, e², e³) è determinata a meno di una trasformazione di Lorentz Λ(m)∈ℒ(M)_m, per effetto della quale la connessione ω si trasforma secondo la relazione

ω→Λ^-1 ω Λ+Λ^-1 dΛ. (10)

È dunque possibile scegliere Λ in maniera che ω si annulli nel punto m∈M (non in ogni punto, però, se non quando R=0). Sotto la trasformazione (10) la curvatura si trasforma omogeneamente, R→Λ^-1 RΛ, mentre le identità di Bianchi (9) restano invariate.

La separazione fra inerzia e gravitazione, che stava alla base del postulato dell'esistenza di uno spazio-tempo assoluto, perde quindi il suo significato oggettivo. In una base naturale su T_m(M), nella quale cioè e_α=∂/∂x^α, dove (x⁰ x¹, x², x³) è un sistema di coordinate locali su M, l'equazione della geodetica, che è l'equazione del moto di una particella puntiforme sotto l'azione dell'inerzia e della gravità, assume la forma

dove s è un parametro lungo la curva, s→x^α(s) (α=0, 1, 2, 3), e Γα_βγ sono i coefficienti della 1-forma di connessione di Levi-Civita ω nella base scelta (v. geometria differenziale). I due termini della (11), che rappresentano rispettivamente l'effetto dell'inerzia e della gravitazione, non hanno separatamente significato oggettivo, mentre la loro somma è invariante rispetto a un arbitrario cambiamento di coordinate.

Se Λ è una matrice 4×4 di funzioni Λα_β, tali che, per per ogni m∈M,

l'insieme {Λ:M→SO(3,1)}, che soddisfa la (10), è un gruppo dipendente da sei funzioni arbitrarie, che lascia invariate le identità di Bianchi (9), l'equazione della geodetica (11) e le equazioni di Einstein, e che rappresenta perciò il gruppo di simmetria della relatività generale. Richiedere l'invarianza rispetto a questo gruppo di trasformazioni equivale a postulare che ogni osservatore possa scegliere arbitrariamente i suoi sistemi inerziali scegliendo una funzione Λ:M→SO(3, 1) che annulli localmente la connessione di Levi-Civita (10).

Ci troviamo qui per la prima volta di fronte a una simmetria locale anziché globale, la quale, invece di dipendere da un numero finito di parametri, dipende da sei funzioni arbitrarie. Una invarianza così vasta è una conseguenza necessaria della richiesta che la dinamica e non soltanto la cinematica possa essere ricondotta alla geometria. Come è stato dimostrato da Noether (v., 1918; v. anche Weyl, 1932²), l'invarianza rispetto a trasformazioni dipendenti da funzioni arbitrarie dà luogo a leggi di conservazione locali anziché globali, come avviene nel caso di trasformazioni dipendenti da un numero finito di parametri. Questa località delle leggi di conservazione riflette la possibilità di scegliere localmente, anziché globalmente, il sistema di riferimento, ossia l'impossibilità di dare una separazione oggettiva fra inerzia e gravitazione.

5. Estensione dello schema geometrico: le simmetrie interne.

Nella geometria della varietà riemanniana a quattro dimensioni, nella quale si ambienta la gravitazione, l'elettromagnetismo non trova una giustificazione naturale, ancorché sia possibile definire sulla varietà una 2-forma F e la sua forma duale che soddisfano alle equazioni di Maxwell. L'elettromagnetismo trova cioè posto in una varietà riemanniana a quattro dimensioni, ma deve essere postulato ad hoc. Un tentativo fatto da Weyl (v., 1921⁴) di far discendere l'elettromagnetismo dal requisito di invarianza rispetto ad arbitrarie trasformazioni di scala del tensore metrico g, cioè rispetto alla trasformazione g→λg, dove λ è una funzione del posto, urtò contro insormontabili difficoltà. Poco più tardi, però, lo stesso Weyl (v., 1929) riuscì a mostrare che l'origine delle interazioni elettromagnetiche doveva ricercarsi nell'invarianza rispetto ad arbitrarie trasformazioni, dipendenti dalle coordinate dello spazio-tempo, della fase dei campi complessi che descrivono le particelle cariche (trasformazioni di gauge). Anche l'elettromagnetismo, dunque, come la gravitazione, trae la sua origine dall'invarianza della teoria rispetto a un gruppo di trasformazioni locali: per la gravitazione si tratta di trasformazioni locali dei sistemi di riferimento, per l'elettromagnetismo di trasformazione della fase dei campi carichi. Nei due casi, osservatori in punti differenti possono scegliere arbitrariamente il proprio riferimento.

Una trasformazione di fase è rappresentata da un elemento del gruppo U(1), cioè da un numero complesso di modulo uno. In un importante lavoro, Mills e Yang (v., 1954) hanno mostrato che l'idea di Weyl poteva estendersi al caso di particelle la cui fase fosse un quaternione di norma uno, cioè al caso in cui una trasformazione di fase fosse un elemento del gruppo SU(2). Si introduceva così l'idea di trasformazioni di gauge non abeliane, idea che si dimostrò più tardi estremamente fruttuosa, dando luogo a una teoria (Weinberg, 1967; Salam, 1968) che descrive in maniera unificata le interazioni elettromagnetiche e quelle deboli e a un'altra basata su un gruppo diverso, che descrive le proprietà delle interazioni forti (v. Fritzsch e altri, 1973; v. Weinberg, 1973).

Per comprendere questi sviluppi, occorre ricordare che, mentre negli anni venti le forze conosciute erano essenzialmente solo quelle elettromagnetiche e quelle gravitazionali, l'indagine dei fenomeni nucleari e subnucleari, iniziata alla fine del secolo scorso, ma sviluppatasi specialmente dopo la scoperta del neutrone nel 1932, ha rivelato l'esistenza di due nuovi tipi di interazioni, le interazioni forti e quelle deboli (v. particelle elementari: Campi e particelle), che agiscono alle piccole distanze fra le particelle elementari. Lo schema della relatività generale si è rivelato insufficiente a descrivere le proprietà di queste interazioni e i fisici sono stati così condotti ad attribuire in maniera fenomenologica a ogni particella dei gradi di libertà interni, non legati cioè alla geometria dello spazio-tempo. Così le particelle dotate di interazioni forti furono classificate secondo le rappresentazioni irriducibili di un gruppo, SU(2) (trasformazioni unitarie in due dimensioni con determinante uno), che agisce in maniera banale sullo spazio-tempo (gruppo di spin isotopico) e rispetto al quale le interazioni forti sono invarianti. Un'ulteriore invarianza di tali interazioni rispetto a un gruppo U(1) fu più tardi introdotta per giustificare la conservazione nelle interazioni forti di una grandezza additiva, l'ipercarica, e anzi il gruppo di invarianza venne poi esteso da SU(2)×U(1) a SU(3) (v. Gell-Mann e Ne'eman, 1964). Queste proprietà di simmetria, che chiameremo globali, in quanto le trasformazioni ad esse connesse non dipendono dalla posizione delle particelle nello spazio-tempo, hanno permesso di interpretare numerosi fenomeni, quali le relazioni fra le energie dei livelli di nuclei isobarici (v. nuclei atomici: Struttura dei nuclei), le relazioni fra le masse di varie particelle elementari e le regole di selezione di numerose reazioni.

Tuttavia il fatto che queste simmetrie siano peculiari di un solo tipo di interazioni fondamentali (le interazioni forti), mentre sono violate dalle altre, ha condotto a ritenere che esse siano manifestazioni secondarie di proprietà di simmetria esatte, che caratterizzano le interazioni fra quelle che oggi si pensano essere le vere entità fondamentali, cioè i quarks (costituenti dei protoni, dei neutroni, ecc.) e i leptoni (elettroni, neutrini, ecc.) (v. particelle elementari). I gradi di libertà interni di questi enti prendono i nomi pittoreschi di ‛colore', ‛sapore' e ‛famiglia' e le simmetrie ad essi associate, che hanno carattere locale, in quanto dipendono dalla posizione nello spazio-tempo, vanno sotto il nome di simmetrie di gauge, per la loro somiglianza con la teoria di Weyl. Senza voler entrare nei dettagli di queste teorie ancora in fase di sviluppo (v. teorie unificate), ci limiteremo qui ad alcune considerazioni generali sulla loro struttura matematica e sul ruolo che in esse gioca la simmetria.

Una particella dotata di struttura interna può esistere in diversi stati (di ‛colore' o ‛sapore' differenti, per es.), il cui insieme è, in tutti i casi conosciuti, in corrispondenza biunivoca con gli elementi di un gruppo di Lie compatto, come U(1), SU(2), SU(3) ecc., chiamato gruppo di simmetria interna. Indicheremo con G questo gruppo e con G_m, fibra su m, l'insieme degli stati interni di una tale particella dotata di struttura localizzata nel punto m della varietà M, a quattro dimensioni, degli eventi fisici. Supporremo anzi che gli effetti gravitazionali siano trascurabili, così che M possa venire identificata con ???OUT-R???⁴; questa approssimazione è probabilmente accettabile fino a energie piccole rispetto a m_Pc², dove m_P è la massa di Planck, m_P=(ℏc/G)^1/2=2,177×10^-5g=1,218×10¹⁹ GeV/c² (G è la costante della gravitazione, ℏ la costante di Planck divisa per 2π e c la velocità della luce).

Ciascuna fibra G_m, m∈???OUT-R???⁴, è diffeomorfa al gruppo di simmetria interna G e l'unione P=⋃_{m∈???OUT-R???4} G_m di tutte le fibre è il fibrato di cui ???OUT-R???⁴ è la base e G il gruppo di struttura. Se la particella non è soggetta a forze esterne, tutte le fibre possono essere identificate, cosicché il fibrato P diventa banale, P=???OUT-R???⁴×G. In questo caso lo spazio totale di una particella dotata di struttura interna si riduce semplicemente al prodotto dello spazio-tempo per lo spazio delle variabili interne e il gruppo G assume il carattere di una simmetria globale. Grosso modo questo vuol dire che in assenza di interazione è possibile fissare le coordinate nello spazio delle variabili interne indipendentemente dalla posizione nello spazio-tempo.

La struttura matematica di una teoria di gauge è dunque molto simile a quella della relatività generale: il gruppo di struttura interna G prende il ruolo che nella relatività generale ha il gruppo di Lorentz SO(3, 1) e la fibra G_m è l'analogo dell'insieme dei riferimenti inerziali sullo spazio tangente T_m(M). Manca in questo caso, tuttavia, la struttura riemanniana, perché lo spazio delle variabili interne non è legato allo spazio-tempo.

In analogia con il punto di vista della relatività generale, che identifica l'azione di un campo gravitazionale con la curvatura dello spazio-tempo, le teorie di gauge descrivono l'effetto di un campo esterno su una particella dotata di struttura come una curvatura del fibrato P, la quale provoca una distorsione nell'allineamento delle fibre G_m sui diversi punti di ???OUT-R???⁴. Come nella relatività generale, si definisce la corrispondenza fra le fibre su punti diversi di una curva in ???OUT-R???⁴ dando una 1-forma di connessione A a valori nell'algebra di Lie del gruppo di simmetria interna G. La forma di connessione A, chiamata dai fisici ‛potenziale di gauge', permette di definire, come nella relatività generale, la 2-forma di curvatura F, o campo di gauge, legata ad A da una relazione simile alla (8), soddisfacente un'identità di Bianchi (9) e legata alle sorgenti da un'equazione non lineare simile a quella di Einstein.

Come abbiamo visto nel cap. precedente, la connessione A non è univocamente definita. Se è g: ???OUT-R???⁴→G, il valore di g nel punto m∈???OUT-R???⁴ fornisce un'applicazione della fibra G_m in se stessa, g(m):G_m→G_m, che rappresenta un cambiamento di coordinate nello spazio interno della particella nel punto m, chiamata trasformazione di gauge. In corrispondenza di tale cambiamento delle coordinate interne, la connessione A si trasforma secondo la relazione

g:A→g^-1 A g+g^-1dg, (12)

mentre la forma di curvatura si trasforma in maniera omogenea:

g:F→g^-1 F g. (13)

Nel caso particolare che G sia il gruppo abeliano U(1), il termine non lineare nella definizione della curvatura (8) si annulla e l'equazione che si ottiene, F=dA, coincide con la ben nota espressione del campo elettromagnetico in funzione del potenziale vettore. A sua volta l'identità di Bianchi (9) si riduce all'equazione omogenea di Maxwell, dF=0, mentre la trasformazione (12) della connessione coincide con la ben nota trasformazione del potenziale vettore. L'elettromagnetismo appare dunque come una teoria di gauge il cui gruppo di struttura è il gruppo abeliano U(1) e la trasformazione di gauge g:???OUT-R???⁴→U(1) rappresenta, in questo caso, come aveva mostrato Weyl, una trasformazione di fase.

Se invece il gruppo di simmetria interna non è abeliano, le equazioni della teoria sono, come nel caso della relatività generale, non lineari e in esse appaiono esplicitamente i potenziali di gauge. Come è stato detto più sopra una teoria basata sul gruppo SU(2)×U(1) sembra dare una descrizione unificata delle interazioni elettrodeboli, realizzando una sintesi fra fenomeni diversi non dissimile da quella maxwelliana che aveva portato all'unificazione dei fenomeni elettrici e magnetici. Le quattro componenti indipendenti del potenziale di gauge A (1-forma di connessione) di questa teoria sono il potenziale vettore del campo elettromagnetico e i tre campi mesonici vettoriali che mediano le interazioni deboli.

Una delle caratteristiche più importanti di questa teoria di gauge, diretta conseguenza della sua simmetria, è quella di essere rinormalizzabile (v. 't Hooft, 1971), cioè di non contenere divergenze peggiori di quella dell'elettrodinamica quantistica. Soltanto immergendo la teoria elettromagnetica e quella delle interazioni deboli in una più vasta, dotata di una più ampia simmetria locale con gruppo di struttura SU(2)×U(1), è stato possibile eliminare le divergenze peggiori che per tanti anni avevano impedito di formulare una teoria soddisfacente delle interazioni deboli. Nel capitolo successivo accenneremo al problema di come nasca la separazione fra fenomeni elettromagnetici e deboli.

Un'altra teoria di gauge, detta cromodinamica, basata sul gruppo SU(3)_c che agisce sulle variabili di colore, sembra dare una descrizione corretta delle interazioni forti (v. Fritzsch e altri, 1973; v. Weinberg, 1973). Anche in questo caso la simmetria locale conduce a una teoria rinormalizzabile. Finalmente sono stati proposti diversi modelli di teorie di gauge che unificano le interazioni forti, elettromagnetiche e deboli, basate sui gruppi SU(5) (v. Georgi e Glashow, 1974), SO(10) (v. Fritzsch e Minkowski, 1976) e sul gruppo di Lie eccezionale E(6) (v. Gürsey e altri, 1976).

Le teorie di gauge, la cui validità resta peraltro ancora da verificare in dettaglio, rappresentano un passo avanti verso la realizzazione dell'ideale di Riemann e di Einstein di dare una descrizione geometrica della fisica. Non è stato ancora trovato il modo di unificare la gravitazione alle altre interazioni e così si hanno al momento due distinte teorie con struttura matematica assai simile: l'una per la gravitazione e l'altra per le interazioni forti ed elettrodeboli, tutte e due dipendenti da simmetrie locali, tutte e due altamente non lineari. Ambedue le teorie sono di natura essenzialmente geometrica, ma lo spazio in cui sono ambientate non è lo stesso nei due casi; esse, come diceva Weyl (v., 1921⁴), riferendosi alla sola gravitazione, ‟segnano la fine dell'idea che la geometria possa esistere indipendentemente dalla fisica".

6. L'origine dell'asimmetria.

a) La rottura spontanea della simmetria.

Nonostante la simmetria delle leggi fisiche, gli stati realizzati in natura sono visibilmente asimmetrici. Ciò è spesso dovuto all'asimmetria delle condizioni al contorno, ma si conoscono anche numerosi casi in cui leggi e condizioni al contorno invarianti rispetto a un gruppo G danno luogo a stati stabili invarianti solo rispetto a un sottogruppo di G. Per esempio, le posizioni medie dei tre atomi identici di una molecola di ozono O₃, fra i quali agiscono forze invarianti per rotazione, non formano un triangolo equilatero, ma un triangolo isoscele il cui angolo al vertice è di circa 58°30′. Nei cristalli e nei cristalli liquidi le interazioni fra gli ioni o gli atomi dipendono solo dalle distanze relative e sono perciò invarianti rispetto al gruppo euclideo E(3) generato dalle traslazioni e dalle rotazioni dello spazio; ciononostante, la disposizione regolare degli atomi nel cristallo definisce nello spazio delle direzioni privilegiate e il gruppo di simmetria G del cristallo è quindi un sottogruppo discreto di E(3) (v. gruppi). La materia del mondo in cui viviamo è fatta di protoni, neutroni ed elettroni, mentre le antiparticelle corrispondenti possono essere solo prodotte artificialmente: la materia non è dunque simmetrica rispetto al gruppo di invarianza Z₂ delle interazioni fondamentali, generato dalla coniugazione di carica.

È noto da molto tempo che al variare di qualche parametro la simmetria può cambiare spontaneamente, cioè senza l'intervento di cause esterne asimmetriche. Al diminuire dell'entropia l'ordine cresce e conseguentemente la simmetria diminuisce. Quando la temperatura di un cristallo scende al disotto di una temperatura critica T_c, può accadere che il gruppo di simmetria cambi e si produca quella che si chiama una transizione di fase di seconda specie. Per esempio, il titanato di bario, BaTiO₃, al disopra di T_c=393 °K è un cristallo appartenente al sistema cubico corrispondente al gruppo puntuale O_h, mentre al disotto di T_c ha una simmetria tetragonale (gruppo puntuale D_4h). Il cambiamento di simmetria è dovuto a una separazione fra il centro di massa delle cariche positive (Ba⁺⁺, Ti⁺⁺⁺⁺) (v. fig. 2) e quello delle cariche negative (30^--), con conseguente comparsa di un momento di dipolo elettrico. Un fenomeno simile si presenta nei materiali ferromagnetici, nei quali, al disotto di una temperatura critica T_c, si desta una magnetizzazione spontanea μ che viola l'invarianza delle interazioni rispetto al gruppo SO(3). In virtù della simmetria del problema, ogni direzione di magnetizzazione è ugualmente probabile e il realizzarsi dell'una o dell'altra direzione dipende da piccole asimmetrie inevitabilmente presenti o anche semplicemente dalle fluttuazioni. Al disotto di T_c esistono perciò infinite soluzioni, ciascuna invariante rispetto a un diverso sottogruppo O(2)_μ⊂SO(3) (rotazioni rispetto all'asse μ). Una singola soluzione viola la simmetria originaria, ma l'insieme di tutte le soluzioni (la sfera di raggio ∥μ∥) è invariante rispetto a SO(3).

b) Biforcazioni con rottura di simmetria.

Il nascere di una polarizzazione elettrica o magnetica al decrescere della temperatura è un esempio di cambiamento di simmetria che avviene a un punto di biforcazione T_c. In generale gli stati di un sistema fisico sono determinati dalle soluzioni dell'equazione funzionale

F(λ, u)=0, (14)

dove λ è un parametro reale, u un elemento di uno spazio funzionale B₁ e F un'applicazione di ???OUT-R???×B₁ in un altro spazio funzionale B₂, tale che u=0 sia una soluzione della (14) per ogni valore di λ. Diremo che λ₀ è un punto di biforcazione di F (v. fig. 3), se in ogni intorno di λ₀ esistono punti (λ, u)∈???OUT-R???×B₁ con u≠0 tali che F(λ, u)=0 (v. Prodi e Ambrosetti, 1973). Se F è invariante rispetto a un gruppo G e u è una soluzione della (14), anche gu, g∈G, è una soluzione. In generale gu è diversa da u, cioè la soluzione di un sistema simmetrico non possiede necessariamente la stessa simmetria del problema. Si dice gruppo di isotropia di u il sottogruppo di G, G_u={g∈G∣gu=u}, che lascia u invariata. Se G_u= G, la soluzione u si dice simmetrica, in caso contrario asimmetrica; la soluzione u=0 è ovviamente simmetrica.

L'insieme Ω di tutte le soluzioni ottenute da una soluzione data per azione di G si chiama orbita di G su B₁:Ω={g u∣F(λ, u)=0, g∈G}, ed è una funzione di λ e di tutti gli invarianti indipendenti costruiti a partire da u. È facile vedere che i gruppi di isotropia di due elementi di Ω, u e gu sono coniugati, cioè G_gu=g G_ug^-1. Questa relazione di coniugazione fra i gruppi di isotropia di due soluzioni non è sufficiente a stabilire la loro appartenenza alla stessa orbita. L'insieme di tutte le orbite i cui gruppi di isotropia sono coniugati è chiamato strato (v. Michel e Radicati, 1971 e 1973). In generale l'insieme delle soluzioni della (14) si ripartisce per l'azione di G in strati e questi in orbite: mentre due soluzioni appartenenti alla stessa orbita sono fisicamente indistinguibili, in quanto si possono ottenere l'una dall'altra con una trasformazione che lascia invariante il problema, ciò non è più vero per due soluzioni che appartengono a orbite caratterizzate da valori diversi degli invarianti del gruppo.

Nei problemi di biforcazione accade spesso che, per λ≥λ₀, la soluzione u=0 (rappresentata tratteggiata nella fig. 3) divenga instabile. Il sistema passa quindi, all'aumentare di λ, dal regime u=0 a quello u≠0. Spesso la soluzione che si biforca a λ=λ₀ possiede una simmetria diversa da quella di u=0. Si ha, in questo caso, una biforcazione con rottura spontanea di simmetria, dove l'aggettivo ‛spontanea' sta a indicare che nessuna causa esterna è venuta a rompere la G-invarianza dell'equazione (14).

Un esempio semplice di biforcazione è fornito dall'equazione

Il gruppo G generato dall'involuzione u→−u è un gruppo di simmetria della (15). Poiché un polinomio pari ha sempre un estremo all'origine, u=0 è una soluzione della (14) invariante per il gruppo G. Per λ>0 compaiono due nuove soluzioni, u₊=√-λ-, u_-=−√-λ-, che sono i minimi di u⁴−2λu² e che sono i due elementi di un'orbita di G. La superficie E=u⁴−2λu² è rappresentata in funzione di u e λ nella fig. 4, che mostra come, procedendo lungo la ‛valle' da valori negativi di λ, si arrivi a una biforcazione a λ=0. Quale delle due valli imboccherà una pallina che rotoli lungo la valle principale dipende dal caso: il risultato finale sarà comunque una rottura della G-simmetria.

Landau (v. Landau e Lifshitz, 1967) ha proposto che il fenomeno della polarizzazione spontanea e le transizioni di fase di seconda specie siano descrivibili, in prima approssimazione, con un'equazione del tipo della (15). Nel caso della magnetizzazione spontanea, per esempio, la (15) deve interpretarsi come una condizione di minimo per l'energia, con λ proporzionale alla differenza T−T_c fra la temperatura e la temperatura critica. Al punto di biforcazione T=T_c si ha il passaggio dallo strato simmetrico ∥μ∥=0 a quello asimmetrico ∥μ∥>0, nel quale le soluzioni hanno gruppi di isotropia coniugati a O(2)_μ.

La (15) dà pure una descrizione qualitativa di un altro importante fenomeno: il nascere della convezione in un fluido quando il gradiente di temperatura supera un valore critico. Questo fenomeno, che gioca un ruolo determinante nell'astrofisica e nella geofisica, è stato studiato in dettaglio sperimentalmente, in condizioni semplificate, da Bénard (v., 1900). Egli osservò che in un liquido contenuto fra due piani orizzontali, scaldato dal basso, il trasporto di calore avviene per conduzione (soluzione simmetrica u=0 della 15) fino a che il numero di Rayleigh R, proporzionale al gradiente di temperatura, è inferiore a un certo valore critico R_c, che dipende dalle condizioni al contorno. Quando R supera il valore critico R_c, si stabiliscono nel recipiente dei moti convettivi (strato asimmetrico con u≠0) e il liquido, che prima era omogeneo, e quindi invariante rispetto al gruppo euclideo del piano (strato simmetrico), si divide in celle, come indicato schematicamente nella fig. 5 (strato asimmetrico). Questa configurazione non è più invariante rispetto al gruppo euclideo, ma solo rispetto a un suo sottogruppo discreto che dipende dalla forma del recipiente (oltre che dalla tensione superficiale). La (15) può ancora interpretarsi come la condizione di minimo dell'energia: in questo caso u rappresenta, per esempio, le velocità in un punto fisso delle celle e λ=R−R_c.

Un altro famoso problema di biforcazione con rottura spontanea di simmetria è quello di determinare la superficie di equilibrio di un fluido omogeneo e incompressibile autogravitante in rotazione rigida rispetto a un asse, con momento angolare J. Il problema, che ha la simmetria di un ellissoide di rivoluzione intorno a J (gruppo di invarianza D_∞h), è della forma (14) con λ=J². Esso ammette uno strato di soluzioni simmetriche (gruppo di isotropia D_∞h), rappresentanti ellissoidi di rivoluzione caratterizzati dalla eccentricità meridiana ε che cresce con J² (ellissoidi di Maclaurin). Nel 1834 Jacobi dimostrò che, per J²≥J²₀=0,384 436..., appare un nuovo strato di orbite, caratterizzate da ε e dall'eccentricità equatoriale η, in cui, cioè, la simmetria assiale è spontaneamente rotta. Ogni elemento dell'orbita Ω(ε, η) è un ellissoide a tre assi il cui gruppo di invarianza è D_2h⊂D_∞h. Questi ellissoidi rappresentano le figure di equilibrio stabile per J²>J²₀ ( v. fig. 6).

Più tardi Poincaré (v., 1885) dimostrò che, per J²>J²_P=0,632 243..., la simmetria rispetto al centro di massa si rompe spontaneamente e compaiono nuovi strati di soluzioni, ciascuna delle quali ha come gruppo di isotropia un gruppo C_2v. Recentemente è stata trovata (v. Constantinescu e altri, 1979) un'altra famiglia infinita di biforcazioni caratterizzata da un numero intero n: la soluzione che appare all'n-esima biforcazione è invariante per rotazioni di un angolo di 2π/n rispetto all'asse di rotazione. Osserviamo che in tutti i casi sopraelencati il piano per il baricentro ortogonale all'asse di rotazione è un piano di simmetria della figura di equilibrio e, come ha dimostrato Lichtenstein (v., 1933), questa simmetria non può scomparire spontaneamente. È possibile che a un meccanismo simile a quello qui descritto siano dovute le forme asimmetriche delle galassie, che sono fra i pochi oggetti astronomici i cui momenti angolari sono dell'ordine dei momenti angolari critici ai quali la rottura della simmetria assiale può avere luogo.

Caratteristica essenziale di tutti i problemi in cui si ha rottura spontanea della simmetria è la non linearità dell'applicazione F nella (14), senza la quale l'asimmetria non può prodursi (v. Sattinger, 1980). Questo spiega perché la rottura spontanea giochi un ruolo determinante nell'idrodinamica, nella fisica dei plasmi e, come vedremo, nelle teorie di gauge non abeliane, anch'esse altamente non lineari.

c) La rottura spontanea della simmetria nelle teorie di gauge non abeliane.

Uno degli aspetti meno soddisfacenti della fisica nucleare e subnucleare, fino a una quindicina di anni fa, era il carattere approssimato delle simmetrie delle interazioni fondamentali: non erano simmetrie vere della teoria, ma soltanto di una parte di essa. È stato uno dei successi più notevoli della fisica delle particelle elementari degli ultimi anni l'aver dimostrato che è possibile, partendo da una teoria di gauge con gruppo di struttura G (SU(5), per es.), che descrive esattamente l'interazione fra i campi fondamentali, generare, per rottura spontanea, le interazioni osservate nel regime di energia normalmente accessibile. Il requisito che la teoria esatta debba contenere in sé le interazioni effettivamente osservate pone delle restrizioni sui possibili gruppi di struttura G, poiché si richiede che la rottura spontanea della simmetria locale rispetto a G dia luogo a una teoria localmente invariante rispetto a SU(3)_c×SU(2)×U(1), dove SU(3)_c è il gruppo di invarianza locale delle interazioni forti (cromodinamica) e SU(2)×U(1) quello delle interazioni elettrodeboli. Il gruppo G deve pertanto contenere come sottogruppo SU(3)_c×SU(2)×U(1): la scelta G=SU(5) è la più semplice, ma, come si è detto prima, SO(10) ed E(6) sono altre scelte possibili.

Il fenomeno di rottura spontanea della simmetria di gauge è assai più complicato di quelli discussi nella precedente sezione: si tratta di rompere spontaneamente non una simmetria globale, ma una locale, generando da una teoria di gauge G-invariante due diverse teorie di gauge con simmetria minore. Il parametro che determina al suo variare il passaggio da una simmetria all'altra è l'energia, o, se si preferisce, ancora la temperatura. Basandosi su estrapolazioni plausibili, seppure non ancora sufficientemente verificate, si pensa oggi che, per energie superiori a E_s≃10¹⁵ GeV, corrispondente a una temperatura T_s≃10²⁸ °K, lo stato della materia possegga la simmetria completa della teoria, cioè sia localmente G-invariante. In queste condizioni tutti i potenziali di gauge del gruppo G corrispondono a particelle con massa nulla. Quando la temperatura scende al disotto della temperatura critica T_s, si produce una transizione di fase e lo stato che si realizza non possiede più la simmetria G, ma solo quella del suo sottogruppo SU(3)_c×SU(2)×U(1). Le interazioni forti si separano così da quelle elettrodeboli; le une e le altre sono descritte da teorie di gauge esatte, ma distinte: la prima, cromodinamica, con gruppo di struttura SU(3)_c, la seconda con gruppo di struttura SU(2)×U(1) (teoria di Weinberg-Salam). All'energia E_w≃10² GeV, corrispondente alla temperatura T_w≃10¹⁵ °K, si produce una nuova transizione di fase: lo stato che si realizza a temperature inferiori a T_w possiede soltanto la simmetria SU(3)_c×U(1), cioè quella delle interazioni forti e quella dell'elettromagnetismo. Non è escluso che a temperature bassissime si producano nuove transizioni di fase con rottura spontanea di SU(3)_c e di U(1)

In corrispondenza di queste transizioni di fase qualcuno dei potenziali di gauge acquista una massa dell'ordine dell'energia critica della transizione (fenomeno di Higgs) e solo quelli relativi al gruppo di simmetria rimanente continuano ad avere massa nulla. Così, dopo la transizione a T_s, restano a massa nulla gli otto campi di gauge del gruppo SU(3)_c e i quattro di SU(2)×U(1). Di questi ultimi solo il potenziale elettromagnetico conserva massa zero dopo la seconda transizione a T_w, mentre i tre potenziali legati alle interazioni deboli (mesoni vettoriali W⁺, Z⁰, W^-) acquistano una massa dell'ordine di un centinaio di GeV.

È ancora prematuro dire se una teoria del genere sarà confermata dagli esperimenti e se potrà essere generalizzata per unificare anche le interazioni gravitazionali al disopra di una nuova temperatura critica T_P≃10³² °K corrispondente alla massa di Planck. Se ciò sarà possibile, la nuova teoria dovrà coinvolgere una simmetria di tipo assai più ampio, come quella delle teorie supersimmetriche, in cui particelle con spin semintero e intero compaiono nella stessa rappresentazione.

Nello studio delle rotture spontanee della simmetria si pone il problema di determinare quali siano le condizioni che determinano una rottura anziché un'altra, o, più precisamente, un gruppo di isotropia rispetto a un altro. Un caso particolare di questo problema riguardante una simmetria globale (SU(3)), probabilmente estendibile a una teoria di gauge, è stato studiato da Michel e Radicati (v., 1971 e 1973), ma molto lavoro resta ancora da fare per poter giungere a una soluzione generale del problema (v. Sattinger, 1980).

Non è affatto detto che il meccanismo di rottura spontanea della simmetria sia l'unico modo di generare l'asimmetria che si osserva in natura. Si conosce per lo meno un meccanismo diverso, in cui, al variare di un parametro, la simmetria cambia in maniera molto diversa da quella qui descritta. Ciò avviene quando il gruppo stesso dipende da un parametro, come, per esempio, il gruppo di Poincaré o il gruppo di de Sitter. In questi casi, quando il valore del parametro raggiunge un valore critico (c=∞, per il gruppo di Poincaré), è la natura stessa del gruppo che cambia, ma il nuovo gruppo non è un sottogruppo del gruppo iniziale. L'importanza di questo fenomeno, chiamato ‛contrazione del gruppo' da Inonu e Wigner (v., 1952), non è stata investigata in dettaglio.

d) Ordine e simmetria.

Strettamente legato al problema della rottura spontanea della simmetria è quello dell'insorgere delle forme nelle strutture dissipative. È questo un campo di studi relativamente nuovo, nel quale, peraltro, i metodi basati sulla teoria dei gruppi non si sono ancora imposti (tuttavia, v. Sattinger, 1980). Alcuni esempi di come in un sistema completamente disordinato soggetto ad azioni esterne possano nascere strutture ordinate sono stati menzionati nel È b. Tipico è il caso del fenomeno di Bénard, nel quale il flusso di energia dà luogo a una grande varietà di forme, talune semplici, come i rulli della fig. 5, che ricordano quelli delle nuvole prodotte dalla convezione nell'atmosfera, altre assai più complicate ed eleganti. La fluidodinamica è ricchissima di fenomeni in cui il flusso di materia può, in determinate condizioni, dar luogo al sorgere di un ordinamento spaziale del fluido che si manifesta in forme svariate e talvolta bellissime.

Ordinamenti spaziali oscillanti nel tempo si producono talvolta in reazioni chimiche particolari, nelle quali l'equilibrio fra i composti chimici presenti si sposta periodicamente. Anche in questo caso si producono figure molto complicate, non statiche, però, ma varianti nel tempo (v. fig. 7). Fenomeni del genere hanno probabilmente analoghi biologici e possono forse anche spiegare alcune caratteristiche della dinamica delle popolazioni.

In tutti gli esempi citati, un flusso di energia o di materia introduce nello stato completamente disordinato, e perciò simmetrico, preesistente, in cui le molecole potevano assumere qualunque posizione e velocità, un ordinamento spaziale e talvolta spazio-temporale determinato da correlazioni a lunga distanza, per cui un gran numero di molecole sono costrette a disporsi in posizioni precise o a muoversi collettivamente. È facile prevedere che lo studio di questi fenomeni collettivi è destinato a gettare luce su problemi con implicazioni in scienze tanto diverse quali la fisica dei laser, la geofisica, la biologia, l'astrofisica, la fisica dell'atmosfera ecc.

7. Conclusioni.

Il fenomeno della rottura spontanea della simmetria suggerisce la possibilità che tutta l'asimmetria osservata nell'universo, a cominciare dall'anisotropia della materia alla scala galattica, possa un giorno essere spiegata per mezzo di leggi simmetriche senza dover introdurre artificialmente condizioni iniziali asimmetriche. Così, per esempio, l'asimmetria fra materia e antimateria potrebbe essere spiegata come fenomeno di rottura spontanea prodottosi quando la temperatura iniziale dell'universo discese sotto un dato valore critico: in quel momento fra le due valli della fig. 4 ne è stata casualmente scelta una, quella del mondo in cui viviamo.

Resta naturalmente il problema di come risalire, dallo studio di fenomeni asimmetrici, alla simmetria delle leggi, o forse, meglio, della legge, della natura. Il punto di vista delle teorie di gauge è che tutte le simmetrie approssimate di quelle che fino a una dozzina di anni fa erano chiamate interazioni fondamentali non siano che manifestazioni secondarie di una nuova teoria dotata di altissima simmetria che si manifesta solo a temperature estreme, quali potevano aversi nei primi istanti dopo l'origine dell'universo. Il raffreddamento dovuto all'espansione dell'universo, già dopo circa 10^-40 s, avrebbe dovuto far scendere la temperatura al disotto della temperatura critica di Planck T_P~10³² °K, alla quale le interazioni gravitazionali si separano dalle altre. È chiaro, quindi, che un'ipotetica teoria supersimmetrica (non ancora esistente) che contenga in sé tutte le interazioni ora note sarebbe la teoria adatta a descrivere la fisica dei primi 10^-40 s. Il fatto che la materia sia passata per uno stato cosi altamente simmetrico può aver lasciato delle tracce indelebili conservatesi durante l'enorme successivo raffreddamento (come, per es., la vita media finita del protone) ed è solo attraverso l'analisi di queste tracce che è possibile sperare di risalire alla simmetria primordiale. Tuttavia è facile rendersi conto di quanto immensa sia l'estrapolazione insita in questi tentativi di ricostruire il corso dell'evoluzione delle leggi fisiche. Le esperienze della fisica delle alte energie possono aiutare a ripercorrere all'indietro questa evoluzione, ma non sembra al momento pensabile che si possano creare artificialmente in piccolo condizioni che si avvicinino a quelle primordiali. Tuttavia è probabile che questa linea di pensiero, in cui microfisica e cosmologia convergono, dominerà le ricerche future della fisica fondamentale.

Questo articolo non si è prefisso lo scopo di esaurire l'argomento della simmetria in fisica, ma ha cercato solo di mettere in luce alcune delle idee emerse in questo secolo, che l'autore giudica più importanti. Molte applicazioni, talune anche di grande rilievo, sono state taciute come, per citarne qualcuna, quelle alla fisica degli stati condensati, a quella dei nuclei e delle particelle elementari. Questo non già perché l'autore giudichi questi argomenti di scarsa importanza ad alcuni di essi ha egli stesso contribuito -, ma perché rappresentano piuttosto applicazioni dei metodi generali discussi nel cap. 3 che non un'introduzione di concetti e di punti di vista nuovi. Su altri argomenti l'autore non ritiene di avere sufficiente competenza e fra questi va menzionato in particolare lo studio dei difetti di simmetria, sviluppatosi negli ultimi anni e che ha già portato a risultati assai interessanti, specie ad opera di L. Michel (v., 1980). A questi l'autore è grato per averlo aiutato a chiarire le proprie idee sul problema della simmetria nel corso di lunghi anni di collaborazione scientifica.

Bibliografia.

Bénard, H., Les tourbillons cellulaires dans une nappe liquide, in ‟Revue générale des sciences pures et appliquées", 1900, XI, pp. 1261-1271, 1309-1328.

Bourgoyne, N., On the connection of spin with statistics, in ‟Nuovo Cimento", 1958, VIII, pp. 607-609.

Cartan, E., Leçons sur la géométrie des espaces de Riemann, Paris 1946.

Cassirer, E., Substanzbegriff und Funktionsbegriff. Untersuchungen über die Grundfragen der Erkenntniskritik, Berlin 1910 (tr. it.: Sostanza e funzione, Firenze 1973).

Constantinescu, D. H., Michel, L., Radicati, L. A., Spontaneous symmetry breaking and bifurcations from the Maclaurin and Jacob sequences, in ‟Le journal de physique", 1979, XL, pp. 147-159.

Curie, P., Sur la symétrie des phénomènes physiques: symétrie d'un champ électrique et d'un champ magnétique, in ‟Journal de physique", 3e série, 1894, III, pp. 393-415.

Dirac, P. A. M., On the theory of quantum mechanics, in ‟Proceedings of the Royal Society", 1926, series A, CXII, pp. 661-677.

Dirac, P. A. M., The quantum theory of the electron, in ‟Proceedings of the Royal Society", 1928, series , CXVII, pp. 610-624.

Dirac, P. A. M., A theory of electrons and protons, in ‟Proceedings of the Royal Society", 1930, series , CXXVI, pp. 360-365.

Einstein, A., Die Grundlagen der allgemeine Relativitätstheorie, in ‟Annalen der Physik", 1916, XLIX, pp. 769-882.

Einstein, A., The meaning of relativity, Princeton 1955.

Engel, F., Über die zehn allgemeinen Integrale der klassischen Mechanik, in ‟Nachrichten von der königlichen Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-physikalische Klasse", 1916, pp. 270-275.

Fermi, E., Zur Quantelung des idealen einatomigen Gases, in ‟Zeitschrift für Physik", 1926, XXXVI, pp. 902-912.

Fierz, M., Über die relativistische Theorie kräftfreier Teilchen mit beliebigem Spin, in ‟Helvetica physica acta", 1939, XII, pp. 3-37.

Fritzsch, H., Gell-Mann, M., Leutwyler, H., Advantages of the colour octet gluon picture, in ‟Physics letters", 1973, XLVII B, pp. 365-368.

Fritzsch, H., Minkowski, P., Parity conserving neutral currents and right handed neutrinos, in ‟Nuclear physics", 1976, CIII B, pp. 61-66.

Gell-Mann, M., Ne'eman, Y., The eightfold way, New York 1964.

Georgi, H., Glashow, S. L., Unity of all elementary particle forces, in ‟Physical review letters", 1974, XXXIII, pp. 438-441.

Gürsey, F., Ramond, P., Sikivie, P., A universal gauge theory model based on E₆, in ‟Physics letters", 1976, LX B, pp. 177-180.

Hamel, G., Die Lagrange-Eulerschen Gleichungen der Mechanik, in ‟Zeitschrift für Mathematik", 1904, L, pp. 1-57.

Heisenberg, W., Mehrkörperproblem und Resonanz in der Quantenmechanik, in ‟Zeitschrift für Physik", 1926, XXXVIII, pp. 411-426.

Heisenberg, W., Über die Spektra von Atomsystemen mit zwei Elektronen, in ‟Zeitschrift für Physik", 1926, XXXIX, pp. 499-518.

Inonu, E., Wigner, E., Representations of the Galilei group, in ‟Nuovo Cimento", 1952, IX, pp. 705-718.

Klein, F., Über die geometrischen Grundlagen der Lorentzgruppe, in ‟Jahresbericht der Deutschen Matematiker-Vereinigung", 1910, XIX, pp. 281-300.

Landau, L., Lifshitz, E., Physique statistique, Moskva 1967.

Lee, T. D., Yang, C. N., Question of parity conservation in weak interactions, in ‟Physical review", 1956, CIV, pp. 254-258.

Lichtenstein, L., Gleichgewichtsfiguren rotierender Flüssigkeiten, Berlin 1933.

Lüders, G., Zumino, B., Connection between spin and statistics, in ‟Physical review", 1958, CX, pp. 1450-1453.

Michel, L., Symmetry defects and broken symmetry configurations hidden symmetry, in ‟Review of modern physics", 1980, LII, pp. 617-651.

Michel, L., Radicati, L. A., Properties of the breaking of hadronic internal symmetries, in ‟Annals of physics", 1971, LXVI, pp. 758-783.

Michel, L., Radicati, L. A., The geometry of the octet, in ‟Annales de l'Institut Henry Poincaré", 1973, XVIII A, pp. 185-214.

Mills, R. L., Yang, C. N., Conservation of isotopic spin and isotopic gauge invariance, in ‟Physical review", 1954, XCVI, pp. 191-198.

Noether, E., Invariante Variationsprobleme, in ‟Nachrichten von der königlichen Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-physikalische Klasse", 1918, pp. 235-257.

Pauli, W., Über den Einfluss der Geschwindigkeitsabhängigkeit der Elektronenmasse auf den Zeemaneffekt, in ‟Zeitschrift für Physik", 1925, XXXI, pp. 373-385.

Pauli, W., Über den Zusammenhang des Abschlusses von Electronengruppen in Atom mit der Komplexstruktur der Felder, in ‟Zeitschrift für Physik", 1925, XXXI, pp. 765-783.

Pauli, W., Über Gasentartung und Paramagnetismus, in ‟Zeitschrift für Physik", 1927, XLI, p. 81.

Pauli, W., The connection between spin and statistics, in ‟Physical review", 1940, LVIII, pp. 716-722.

Pauli, W., Exclusion principle, Lorentz group and reflections of spacetime and charge, in Niels Bohr and the development of physics (a cura di W. Pauli), New York 1955.

Poincaré, H., Sur l'équilibre d'une masse liquide animée d'un mouvement de rotation, in ‟Acta mathematica", 1885, VII, pp. 259-380.

Prodi, G., Ambrosetti, A., Analisi non lineare, Pisa 1973.

Sattinger, D. H., Bifurcation and symetry breaking in applied mathematics, in ‟Bulletin of the American Mathematical Society", 1980, III, pp. 779-819.

T. Hooft, G., Renormalization of massless Yang-Mills Fields, in ‟Nuclear physics", 1971, XXXIII B, pp. 173-193.

Uhlenbeck, G. E., Goudsmit, S., Spinning electrons and the structure of spectra, in ‟Nature", 1925, CXVII, pp. 264-000.

Waerden, B. L. van der, Exclusion principle and spin, in Theoretical physics in the twentieth century (a cura di M. Fierz e V. F. Weisskopf), New York 1960.

Weinberg, S., A model of leptons, in ‟Physical review letters", 1967, XIX, pp. 1264-1266.

Weinberg, S., Non Abelian gauge theory of the strong interactions, in ‟Physical review letters", 1973, XXXI, pp. 494-497.

Weyl, H., Raum, Zeit, Materie, Berlin 1921⁴.

Weyl, H., Gruppentheorie und Quantenmechanik, Leipzig 1928, 1932².

Weyl, H., Elektron und Gravitation, in ‟Zeitschrift für Physik", 1929, LVI, pp. 330-352.

Weyl, H., Philosophy of mathematics and natural sciences, Princeton 1949.

Weyl, H., Symmetry, Princeton 1952.

Wigner, E., Einige Folgerungen aus der Schrödingerschen Theorie für die Termstrukturen, in ‟Zeitschrift für Physik", 1927, XLIII, pp. 624-652.

Wigner, E., Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomspektren, Braunschweig 1931.

Wigner, E., Über die Operation der Zeitumkehr in der Quantenmechanik, in ‟Nachrichten von der königlichen Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse", 1932, pp. 546-559.

Wigner, E., On unitary representations of the inhomogenous Lorentz group, in ‟Annals of mathematics", 1939, XL, pp. 149-204.

Wigner, E., The unreasonable effectiveness of mathematics in the natural sciences, in ‟Communications in pure and applied mathematics", 1960, XIII, pp. 1-14.