simplesso

simplesso

Caso particolare di politopo. Un politopo è l’ente geometrico analogo in spazi euclidei di dimensione n>3 al poligono e al poliedro rispettivamente in 2 e 3 dimensioni.

Partendo dalla dimensione 2, si consideri un piano cartesiano con coordinate (x,y) associabili a punti del piano. Una disequazione lineare nelle variabili (x,y) del tipo x+2y−6≤0 individua un semipiano, ovvero l’insieme di tutti i punti che stanno ‘sotto’ o sulla retta di equazione y=3−(x/2). A n disequazioni lineari corrispondono n diversi semipiani. L’intersezione di più semipiani è l’insieme dei punti appartenenti a tutti i semipiani, cioè soddisfano contemporaneamente tutte le disequazioni. Nei casi in cui tale insieme è limitato (cioè può essere contenuto in un quadrato), esso è tipicamente un poligono, cioè una figura convessa giacente su un piano e delimitata da segmenti che congiungono i vertici del poligono (fig.).

Passando a 3 dimensioni, si possono considerare spazi con coordinate (x,y,z) associabili a punti dello spazio. Una disequazione lineare nelle variabili (x,y,z) del tipo x+2y+4z−16≤0 individua un semispazio, ovvero l’insieme di tutti i punti che stanno sotto o sul piano di equazione z=4−(y/2)−(x/4). A disequazioni diverse corrispondono semispazi differenti e l’intersezione di più semispazi è l’insieme dei punti che appartengono a tutti i semispazi, cioè soddisfano contemporaneamente tutte le disequazioni. Nei casi in cui tale insieme è non vuoto e limitato (cioè può essere contenuto in un cubo), esso è tipicamente un poliedro, cioè una figura convessa delimitata da poligoni giacenti su piani diversi.

Per n>3 dimensioni, l’intuizione geometrica si perde ma possiamo considerare ancora n-ple di coordinate che individuano punti di uno spazio a n dimensioni, disequazioni lineari nelle n variabili, semispazi n dimensionali e intersezioni di più semispazi. Ove tale insieme sia non vuoto e limitato (sia contenuto in un ipercubo), esso è ancora un ente convesso detto politopo. Un s. è un politopo con il minor numero di vertici, analogo al triangolo nel piano (due dimensioni) e al tetraedro nello spazio tridimensionale.

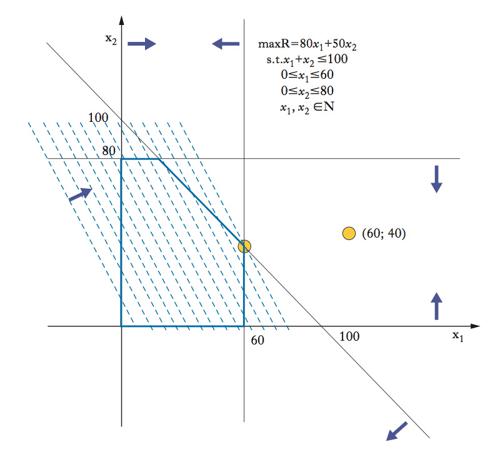
Di particolare interesse nelle applicazioni, il metodo del s. per la soluzione di problemi di programmazione lineare, cioè di ottimizzazione (per es. massimizzazione) di una funzione lineare F(x) detta funzione obiettivo, per x vincolato (attraverso un sistema di vincoli espressi da disequazioni lineari) ad appartenere a un politopo. Il metodo di soluzione (detto algoritmo del s.), dovuto a G. Dantzig (➔), sfrutta l’idea che il punto di ottimo deve necessariamente coincidere con uno dei vertici del politopo.