Simulazioni numeriche
Simulazioni numeriche
La modellistica matematica mira a descrivere in termini matematici i molteplici aspetti del mondo reale e la loro dinamica evolutiva. Essa costituisce la terza colonna portante nelle scienze e nell’ingegneria, a completamento delle due più tradizionali che sono l’analisi teorica e la sperimentazione. Oggi il ruolo della modellistica matematica è ampiamente consolidato in svariati settori, per esempio quello industriale e ambientale, mentre sta diventando sempre più evidente il potenziale contributo che essa può apportare in numerosi altri ambiti.
Una ragione del suo crescente successo è senza dubbio lo sviluppo impetuoso del calcolo scientifico, quella disciplina che consente di tradurre un modello matematico (risolubile in forma esplicita solo in rarissime situazioni) in algoritmi che possono venire trattati e risolti da calcolatori di potenza sempre più elevata.
I modelli matematici si ottengono spesso per astrazione. Peraltro, l’innovazione richiede flessibilità, la flessibilità richiede astrazione e il linguaggio dell’astrazione è la matematica. Quest’ultima tuttavia non è solo linguaggio, essa approfondisce la conoscenza, ricerca soluzioni ottimali, progetta algoritmi efficienti. Innovazione tecnologica e matematica possono in tal modo dare vita a un processo di interazione virtuoso.
Sin dall’inizio degli anni Sessanta l’analisi numerica, ovvero la disciplina che consente la risoluzione di equazioni matematiche (algebriche, funzionali, differenziali e integrali) attraverso algoritmi, ha avuto un ruolo guida nella risoluzione di problemi associati a modelli matematici derivanti dall’ingegneria e dalle scienze applicate. Sulla scia di questo successo nuove discipline si sono aperte all’uso della modellistica matematica, quali la tecnologia dell’informazione e della comunicazione, la bioingegneria, l’ingegneria finanziaria e molte altre.
La straordinaria complessità di queste applicazioni ha spronato i matematici a riconsiderare il loro approccio ponendo al centro della scena il problema in quanto tale e cercando modelli e algoritmi per trovarne soluzioni. Questo cambio di paradigma ha determinato l’avvento del calcolo scientifico, il cui scopo consiste nella costruzione di algoritmi migliori per una simulazione efficace e accurata nonché per l’ottimizzazione di problemi di interesse reale.
In effetti, i modelli matematici offrono nuove possibilità per dominare la crescente complessità delle tecnologie alla base della produzione industriale moderna; esplorando rapidamente nuove soluzioni, permettono di accelerare i cicli di innovazione. Essi forniscono un contributo irrinunciabile alla progettazione in numerosi ambiti industriali, con lo scopo di ridurre il ciclo temporale necessario per la concezione di un nuovo prodotto (per es., un aereo o un’automobile). Ciò assicura un vantaggio potenziale alle aziende, consentendo loro di ridurre i costi ricorrendo sempre di meno agli onerosissimi collaudi, ma anche risparmiando tempo prezioso nella stessa fase di sviluppo.
In sintesi, possiamo affermare che la modellistica matematica e il calcolo scientifico stanno gradualmente ma inesorabilmente affacciandosi in molteplici contesti per proporsi come strumento ausiliario, quando addirittura non esclusivo, di indagine qualitativa e quantitativa.
Nel seguito verrà discusso il ruolo della modellistica matematica e del calcolo scientifico nelle scienze applicate, la loro rilevanza come strumenti di simulazione, l’indagine e il supporto alle decisioni, il loro contributo all’innovazione tecnologica. Si citeranno alcuni risultati conseguiti e le prospettive che si aprono in svariati settori quali: l’industria, l’ambiente, le scienze della vita e lo sport.
Il calcolo scientifico per l’innovazione tecnologica
Combinato con l’aumento vertiginoso della velocità dei computer, il calcolo scientifico può divenire fattore decisivo nella determinazione del confine tra complessità trattabili o al contrario inaccessibili. Suo obiettivo ultimo è la realizzazione di modelli versatili e affidabili, accurati entro confini dettati dalla specifica classe di problemi da trattare, verificati su una grande e significativa varietà di casi prova analogici o sperimentali, per i quali si disponga di soluzioni di riferimento.
Oltre ai concetti universali che un modello matematico deve riprodurre – quali, per esempio, la conservazione della massa e dell’energia di un fluido o del momento d’inerzia di una struttura – per una simulazione numerica di successo è necessario stabilire quale livello di dettaglio ha senso inserire nelle diverse componenti di un modello e quali semplificazioni apportare in modo da favorire una sua integrazione con modelli diversi.
Modelli che simulino realtà molto complesse dovrebbero anche tener conto dell’incertezza che deriva da insufficiente disponibilità dei dati che alimentano il modello stesso. L’analisi del rischio, che deriva dall’incertezza e dall’esposizione alla sconfitta (sia essa riduzione del profitto, danno all’ambiente, compromissione della salute o altro) è un’ulteriore proprietà che un buon modello dovrebbe possedere. Modelli che godano di queste proprietà saranno usati per prevedere processi naturali, biologici, ambientali, per comprendere meglio la fisica di fenomeni complessi e contribuire alla progettazione di prodotti e tecnologie innovative.
Un aspetto importante nel calcolo scientifico è rappresentato dalla fluidodinamica computazionale (CFD), la disciplina che mira a risolvere al calcolatore i problemi governati da fluidi. Nel settore aerospaziale, per esempio, la CFD trova numerosissime applicazioni. Modelli numerici basati sulle equazioni del flusso a potenziale oppure su quelle più sofisticate di Euler o di Navier-Stokes si usano, per esempio, per l’analisi aerodinamica dei profili alari o dell’intera fusoliera, per massimizzare le prestazioni (riducendo la resistenza al moto) ma anche per incrementare la sicurezza o ridurre l’inquinamento atmosferico e acustico. La simulazione si accompagna spesso al controllo e all’ottimizzazione, con l’obiettivo di progettare dispositivi o aerei che soddisfino criteri prestabiliti: maggiore affidabilità strutturale, migliori prestazioni aerodinamiche, minor impatto ambientale grazie alla riduzione di emissioni di rumore nel caso di aerei commerciali, massimizzazione della velocità e miglioramento della manovrabilità nel caso di aerei militari.
La risoluzione di questi problemi richiede algoritmi di ottimizzazione multiobiettivo (di tipo deterministico, stocastico o genetico). Sempre nell’ambito aeronautico, modelli di propagazione elettromagnetica servono per simulare campi elettromagnetici esterni al fine di evitare che questi interferiscano in modo dannoso con quelli generati dai numerosi circuiti elettronici parte integrante degli impianti e della strumentazione di bordo. Si impiegano modelli per simulare gli sforzi e le deformazioni di componenti sensibili dell’aereo (per la simulazione dell’analisi dell’affaticamento dei materiali), con l’obiettivo di migliorare la stabilità strutturale e quella dinamica attraverso la simulazione numerica dell’interazione tra fluido e struttura.
Analisi simili sono effettuate nell’industria automobilistica, dove la simulazione numerica entra ormai virtualmente in tutti gli aspetti della progettazione e della produzione dei veicoli. Si usano modelli per la simulazione della combustione interna ai motori allo scopo di consumare meno carburante, accrescere la qualità delle emissioni, ridurre il rumore. Inoltre, il miglioramento delle prestazioni, la sicurezza o anche il comfort richiedono la risoluzione di equazioni della dinamica dei fluidi esterni e interni, dell’aeroelasticità, della dinamica delle vibrazioni aeroacustiche, dello scambio termico, della cinetica chimica per la combustione, delle onde d’urto (si pensi alla fase di apertura di un air-bag), della meccanica delle strutture in regime di grandi sforzi e grandi deformazioni per simulare le conseguenze dovute a impatti.
L’industria chimica fa uso di modelli matematici al fine di simulare processi di polimerizzazione, stampaggio o estrusione per materiali a reologia complessa, dove l’analisi macro tipica della meccanica dei continui deve coniugarsi a quella micro, più adatta a descrivere le delicate e complesse leggi costitutive di materiali con nanostruttura. Ciò richiede lo sviluppo di tecniche di indagine e di algoritmi multiscala, capaci cioè di descrivere e catturare lo scambio di processi meccanici, termici e chimici fra scale spaziali notevolmente eterogenee.
Nell’industria elettronica la simulazione delle equazioni di deriva-diffusione, idrodinamiche, di Boltzmann o di Schrödinger costituisce uno strumento decisivo per progettare circuiti integrati sempre più piccoli e veloci, con funzionalità crescente e con consumi sempre più ridotti (fondamentali per es., nelle molteplici applicazioni della telefonia mobile).
Algoritmi efficienti servono inoltre per la codifica e la decodifica di messaggi fra multiutenti.
Modellare il tempo
Negli ultimi decenni il problema di enorme rilevanza pratica della previsione meteorologica a breve termine (giornaliero o settimanale) si è collegato sempre più strettamente a quello della previsione per i prossimi decenni, o addirittura per un intero secolo, dell’evoluzione del clima e dei livelli di inquinamento atmosferico.
Fortunatamente, in natura esistono normali variazioni climatiche su scala regionale che obbediscono a leggi fisiche e sono pertanto descritte e simulate con modelli matematici. Anche a livello globale (continentale o planetario) ve ne sono di legate a fenomeni deterministici, come la variazione dell’inclinazione dell’asse terrestre per effetto di imponenti assestamenti delle placche telluriche, l’eccentricità dell’orbita terrestre, la circolazione oceanica o i fenomeni geologici di particolare intensità come l’eruzione di vulcani ad alta intensità energetica.
Il problema della previsione meteorologica è stato formulato compiutamente come problema matematico solo all’inizio del XX sec. a opera del matematico norvegese Vilhelm Bjerknes, il quale descrisse il moto dell’atmosfera utilizzando le equazioni di Euler per la dinamica di un gas perfetto (già ben note all’epoca) opportunamente modificate per tener conto dell’azione della forza di gravità e del moto di rotazione terrestre.
Purtroppo, i dati relativi allo stato dell’atmosfera erano disponibili in un numero relativamente limitato di punti, si riferivano a variabili spesso eterogenee e a istanti di tempo diversi. Inoltre le equazioni di Euler descrivono una gamma estremamente ampia di moti dell’atmosfera, che possono avere luogo su scale spaziali e temporali diverse tra loro di molti ordini di grandezza (centimetri piuttosto che chilometri, secondi piuttosto che giorni). L’assenza di dati relativi ad alcune di queste scale può portare alla generazione di moti spuri (che non esistono in natura) e al deterioramento della qualità delle previsioni. Infine, una descrizione realistica dei fenomeni meteorologici non può ovviamente prescindere dalla previsione della distribuzione del vapore acqueo, dei suoi cambiamenti di fase (da liquido a gassoso) e dalle conseguenti precipitazioni.
Il primo tentativo di affrontare il problema della risoluzione numerica effettiva delle equazioni del moto fu esperito dallo scienziato britannico Lewis Richardson, il cui sforzo pionieristico culminò nel 1922 con il primo esempio di calcolo concreto della soluzione delle equazioni del moto atmosferico su una regione vasta quanto l’intera Europa occidentale.
I risultati ottenuti da Richardson, attraverso complicatissimi calcoli manuali, portarono in realtà a previsioni totalmente errate: in quegli anni mancava infatti una teoria adatta a dominare le insidie delle equazioni da risolvere.
Per condurre a buon fine lo sforzo di Richardson fu decisivo il contributo del suo allievo Carl-Gustaf Rossby. Emigrato negli Stati Uniti negli anni Venti, egli contribuì a fondare il servizio meteorologico per l’aviazione civile e militare durante la Seconda guerra mondiale. Tra i contributi indiretti del suo lavoro si può a buon diritto considerare anche la previsione meteo effettuata dagli americani per individuare il D-day (il 6 giugno 1944) per lo sbarco in Normandia.
I modelli matematici semplificati introdotti da Rossby resero possibile la prima previsione meteorologica con un calcolatore elettronico, risultato della collaborazione avviata a Princeton da John von Neumann e da Jules Charney alla fine degli anni Quaranta. In particolare, fu possibile effettuare una previsione sull’intero Nord America attraverso un modello semplificato che descriveva l’atmosfera come un unico strato di fluido uniforme. Pur richiedendo ventiquattro ore di calcolo sull’unico computer elettronico dell’epoca (l’ENIAC) per effettuare una previsione a sole 12 ore, il lavoro di Charney e von Neumann mostrò per la prima volta che una previsione basata esclusivamente su un modello numerico poteva giungere a risultati qualitativamente e quantitativamente in accordo con la quella realizzabile a partire dagli stessi dati da un meteorologo esperto dell’epoca. Il moderno approccio alla previsione meteorologica numerica era nato.
In effetti, oltre allo spettacolare aumento delle prestazioni dei computer vi sono stati miglioramenti radicali nell’accuratezza degli strumenti matematici di previsione, lo sviluppo di una teoria della predicibilità dei sistemi dinamici caotici, il miglioramento delle tecniche di assimilazione dei dati.
Dagli anni Sessanta alle stazioni di rilevamento a terra si è inoltre aggiunto l’uso sistematico dei rilevamenti effettuati dai satelliti, che costituiscono ormai la parte più rilevante dei dati utilizzati per l’inizializzazione di modelli numerici. Da allora, l’impatto dei progressi scientifici e tecnologici è stato notevolissimo. Si pensi per esempio ad alcune caratteristiche del modello globale IFS dello European Centre for Medium Range Weather Forecast (ECMWF). Esso utilizza una griglia di calcolo con una risoluzione spaziale media di circa 22 km in orizzontale e 90 livelli verticali. Ciò consente di includervi anche parte della stratosfera.
Questo modello può effettuare previsioni a 10 giorni in poco più di un’ora di calcolo su un moderno supercalcolatore parallelo, cui vanno tuttavia aggiunte circa 6 ore necessarie a effettuare la complessa procedura di assimilazione dei dati. Il modello IFS consente di effettuare in modo affidabile la previsione meteorologica per circa 7,5 giorni su scala continentale europea, assai di più dei 5,5 giorni del 1990.
Modelli per le scienze della vita
Pur essendo iniziato da svariati decenni, lo sviluppo di modelli matematici per le scienze della vita deve ancora raggiungere il suo culmine.
La scoperta recente della sequenza completa del patrimonio genetico umano (il genoma) contenuto in ognuna delle nostre cellule rende possibile l’accesso a un insieme di circa 30÷40 mila geni (segmenti con senso compiuto del genoma), i quali codificano circa 250 mila proteine. Eppure, dopo 50 anni di biologia molecolare rimane ancora da chiarire il ruolo dei geni regolatori nella formazione delle proteine. Infatti, se i geni dell’emofilia, del daltonismo, della talassemia sono monofattoriali, quelli che regolano l’altezza, la capacità di resistenza alla fatica, la forma degli occhi o della bocca sono al contrario multifattoriali. La bioinformatica e la modellistica dovranno migliorare la comprensione della genetica dei caratteri multifattoriali.
Ancora più difficile e importante sarà il passo successivo: capire i meccanismi d’interazione di decine di migliaia di proteine nella generazione delle funzioni biologiche. La loro rappresentazione quantitativa nel caso degli esseri umani è oggi chiamata fisioma.
La modellistica matematica è destinata a giocare un ruolo primario nello svelare il modo in cui l’informazione contenuta nel genoma è stata predisposta al fine di creare sistemi viventi. Essa può essere impiegata al livello della cellula, degli organi o anche di apparati come quelli circolatorio o nervoso. A questo fine essa richiederà lo sviluppo di modelli integrati: (a) in senso orizzontale, ovvero basati sull’interazione di differenti processi fisici o biologici alla stessa scala. La comprensione della natura accoppiata di tali processi richiede la messa a punto di diversi modelli computazionali in grado di trattarli singolarmente; (b) in senso verticale, in quanto si debbono usare dati sperimentali e modelli matematici capaci di maneggiare scale spaziali dal livello molecolare (inferiori a 10−9 m) a quello cellulare e tissutale (10−7÷10−3 m), sino alla scala dei vari organi e dell’intero corpo (10−3÷10−1 m).
Nel fornire una comprensione quantitativa del comportamento di un intero organo in termini di funzioni subcellulari, i modelli potrebbero stabilire un legame fra struttura molecolare e comportamenti clinicamente osservabili, semplificando così l’interpretazione di immagini ottenute da risonanza magnetica, ultrasuoni o mappe di potenziali elettrici.
L’analisi quantitativa dell’interazione elettrica, meccanica e biochimica della funzione cardiaca, possibile se si dispone di modelli matematici integrati, può per esempio spiegare il comportamento di una nuova medicina su una membrana che funziona da recettore.
Naturalmente gli scopi e gli obbiettivi dell’indagine matematica e della simulazione numerica cambiano al variare della scala. Durante gli anni Settanta, gli esperimenti in vitro o quelli su animali rappresentavano la modalità principale degli studi cardiovascolari. Recentemente, il progredire della fluidodinamica computazionale (CFD), così come i netti miglioramenti nelle prestazioni informatiche, hanno prodotto significativi passi in avanti che promettono di rivoluzionare la ricerca vascolare.
Grandezze fisiche come lo shear stress (sforzo tangente) sulla membrana endoteliale, assai problematiche da misurarsi in vitro, possono essere calcolate su geometrie reali ottenute con algoritmi di ricostruzione tridimensionale grazie al supporto delle moderne e non invasive tecnologie di acquisizione dei dati (risonanza magnetica nucleare, angiografia digitale, tomografia computerizzata, anemometria doppler).
Fluendo nelle arterie e nelle vene, il sangue interagisce meccanicamente con le pareti dei vasi, dando origine a complessi problemi di interazione fluido-strutturale. In effetti, il fronte dell’onda pressoria trasferisce energia meccanica alle pareti che si dilatano; tale energia viene restituita al flusso sanguigno nella fase di compressione dei vasi stessi.
La simulazione vascolare dell’interazione fra fluido e parete richiede algoritmi che descrivano sia il trasferimento di energia a livello macroscopico tra il fluido (modellato tipicamente dalle equazioni di Navier-Stokes) e la struttura (modellata dalle equazioni della meccanica dei solidi), sia l’influenza a livello microscopico dello shear stress sull’orientamento, la deformazione e il danneggiamento delle cellule endoteliali.
Nel contempo, le equazioni del flusso devono essere abbinate a modelli appropriati per descrivere il trasporto, la diffusione e l’assorbimento delle componenti chimiche presenti nel sangue (come ossigeno, lipidi, farmaci) nei diversi strati che compongono la parete delle arterie (intima, media e avventizia). Simulazioni numeriche di questo tipo possono aiutare a chiarire modificazioni biochimiche prodotte da alterazioni nel campo di flusso, dovute per esempio alla presenza di una stenosi.
Nel sistema cardiovascolare si riscontrano condizioni di flusso separato e moti circolatori secondari, in presenza di vasi a grande curvatura (come l’arco aortico o le coronarie) ma anche a valle di biforcazioni (per es., quella carotidea nei suoi rami interno ed esterno) o di regioni con restrizioni causate dalla presenza di stenosi. Vi sono inoltre zone con inversione del flusso (dalle regioni distali a quelle prossimali) nonché aree a shear stress basso o temporalmente oscillante.
Queste circostanze sono oggi riconosciute quali potenziali fattori nello sviluppo di patologie arteriose. Una comprensione dettagliata del cambiamento emodinamico locale, degli effetti della modificazione delle pareti vascolari sullo schema del flusso e del graduale adattamento nel medio-lungo periodo del sistema globale a seguito di interventi chirurgici è oggi possibile grazie all’uso di raffinate simulazioni al computer e potrebbe rilevarsi estremamente utile nella fase preliminare alla realizzazione di un trattamento terapeutico.
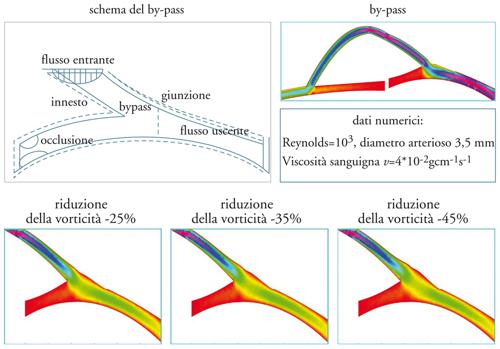
Una prospettiva simile potrebbe fornire specifiche indicazioni quanto al design di procedure chirurgiche. Simulare il flusso in un by-pass coronarico, in particolare la ricircolazione che si determina a valle del reinnesto nella coronaria, può contribuire alla comprensione degli effetti della morfologia delle arterie sul flusso e quindi dell’evoluzione postchirurgica (fig. 6).
La teoria del controllo ottimale di forma può aiutare a progettare un by-pass che minimizzi la vorticità prodotta a valle del reinnesto nella coronaria. Analogamente, lo studio degli effetti delle protesi vascolari e degli impianti di valvole artificiali sull’emodinamica locale e globale può avanzare grazie a simulazioni sufficientemente accurate del campo di flusso del sangue.
In un tale ambito di chirurgia virtuale, il risultato di trattamenti alternativi per un specifico paziente può essere previsto dalle simulazioni. Questo approccio numerico è un aspetto di un nuovo paradigma della pratica clinica conosciuto come medicina predittiva.
Modelli per la simulazione e la competizione
L’applicazione dei modelli matematici non si limita al contesto tecnologico, ambientale o medico. Da diversi anni si adottano infatti modelli deterministici e stocastici nell’analisi di rischio di prodotti finanziari favorendo la formazione di una disciplina nota con il nome di ingegneria finanziaria. La nuova frontiera ha inoltre già iniziato a lambire la sociologia, l’architettura, il tempo libero e lo sport.
Nello sport da competizione, la CFD sta assumendo da alcuni anni un ruolo determinante nella fase di progettazione e analisi delle prestazioni delle automobili di Formula 1. Tuttavia, quello automobilistico non è il solo settore in cui la modellistica matematico-numerica ha fatto il suo ingresso. A questo proposito, un’esperienza interessante è quella che ha visto il gruppo di ricerca di chi scrive impegnato nella Coppa America di Vela conclusasi con la vittoria dell’imbarcazione svizzera Alinghi nel marzo 2003 e poi ancora nel luglio 2007.
Sino a una ventina di anni fa, le diverse squadre di progettisti sviluppavano forme assai diversificate di vele, scafi, bulbi e chiglie. Oggi le varie forme geometriche hanno raggiunto una standardizzazione piuttosto uniforme e anche i più piccoli dettagli possono fare la differenza in termini di risultati. Citando Jerome Milgram, professore del MIT e veterano nella consulenza a diversi team americani di Coppa America, «gli yachts della Coppa America richiedono un’estrema precisione nel design dello scafo, delle parti in acqua e delle vele. Un nuovo scafo che offra una resistenza all’onda ridotta dell’1% può assicurare un guadagno di ben 30 secondi sulla linea d’arrivo».
Per ottimizzare le prestazioni di uno scafo si devono risolvere le equazioni della dinamica dei fluidi intorno all’intera barca, tenendo conto della variabilità di venti e onde, dei diversi regimi di regata (di poppa piuttosto che di bolina), della posizione e del movimento della barca avversaria. Ma va considerata anche la dinamica dell’interazione fra i fluidi presenti (aria e acqua) e le componenti strutturali (scafo, appendici immerse, vele e albero). Infine, va modellata con grande accuratezza la forma e il moto della cosiddetta superficie libera, ovvero dell’interfaccia di separazione fra acqua e aria. Idealmente, un modello completo dovrebbe essere in grado di riprodurre diversi aspetti fisici del problema in oggetto. Da un lato, dovrebbe tenere conto degli effetti dovuti alla viscosità dell’acqua, della transizione tra flusso laminare e flusso turbolento (quello che genera cascate di vortici di dimensioni variabili, dalla micrometrica alla metrica), delle scie turbolente generate dall’interazione del flusso con le parti immerse, della forma dell’onda che si genera sullo scafo. Dall’altro, dovrebbe saper calcolare le deformazioni strutturali che sono assai significative per via dei carichi estremi agenti sullo scafo (sino a 20 tonnellate), sull’albero e soprattutto sulle vele. L’obiettivo è quello di sviluppare con i progettisti le forme ottimali per lo scafo, la chiglia, il bulbo e le alette. Occorre minimizzare la resistenza sott’acqua e massimizzare la spinta indotta dalle vele.
La matematica consente di simulare in laboratorio le diverse situazioni, abbattendo drasticamente costi e tempi necessari a costruire un numero elevato di prototipi da provare in bacini artificiali o nella galleria del vento. Per ogni nuova configurazione proposta dai progettisti (alla fine sarebbero state diverse centinaia) è stato necessario costruire il modello geometrico – servono circa trecento superfici, di tipo splines, per ricoprire il solo scafo – generare la griglia di calcolo sulla superficie di tutti gli elementi della barca di qualità sufficiente per permettere di catturare la transizione fra zone di flusso laminare e di flusso turbolento, generare di conseguenza quella volumetrica nel dominio esterno. Infine, si devono risolvere le equazioni di Navier-Stokes che modellano l’accoppiamento fra i moti dell’aria e dell’acqua e la conseguente forma dell’onda, detta superficie libera, a loro volta completate da equazioni addizionali costituenti i modelli per il calcolo dell’energia turbolenta e del suo tasso di dissipazione.
Tali equazioni non possono essere risolte esattamente, determinando cioè le soluzioni in forma esplicita. La loro risoluzione approssimata richiede l’introduzione di raffinati metodi di discretizzazione, i quali consentano in particolare di trasformare un problema di dimensione infinita in uno di dimensione grande ma finita. Il calcolo tipico, basato su schemi ai volumi finiti, ha richiesto in effetti la risoluzione di problemi non lineari con diverse decine di milioni di incognite. Facendo massiccio ricorso ad algoritmi paralleli, servono fino a 24 ore di tempo dedicato su piattaforme di calcolo parallele a 64 processori per effettuare la simulazione di punta, caratterizzata da oltre 160 milioni di incognite.
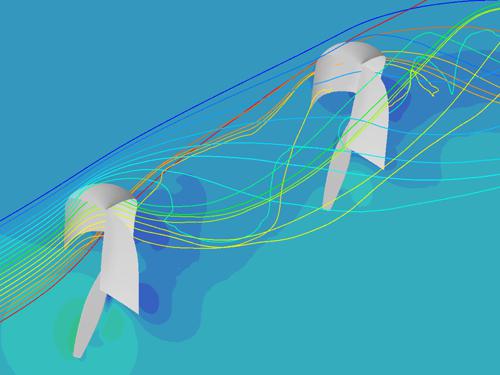
Queste simulazioni consentono al design team di scartare soluzioni all’apparenza innovative e di adottarne altre che garantiscano migliori prestazioni. Inoltre, simulando gli effetti dell’interazione aerodinamica fra due barche si possono determinare la consistenza delle zone d’ombra (le scie con minor vento per via della posizione relativa di una barca rispetto all’altra), la perturbazione del flusso e la vorticità della scia turbolenta che si genera per l’interazione dell’aria, con informazioni preziose per la tattica di gara. Questi studi sono finalizzati a disegnare un’imbarcazione che presenti una combinazione ottimale delle quattro caratteristiche necessarie a un’imbarcazione di Coppa America per risultare vincente: leggerezza, resistenza, velocità, nonché la manovrabilità necessaria per cambiare assetto nel minor tempo possibile (fig. 7).
bibliografia
Parolini, Quarteroni 2005: Parolini, Nicola - Quarteroni, Alfio, Mathematical models and numerical simulations for the America’s Cup, “Computer methods in applied mechanics and engineering”, 194, 2005, pp. 1001-1026.
Quarteroni 2001: Quarteroni, Alfio, Modeling the cardiovascular system - A mathematical adventure, “SIAM news”, 34, 2001 (Part I); “SIAM news”, 34, 2001 (Part II).
Quarteroni 2006: Quarteroni, Alfio, Modellistica numerica per problemi differenziali, 3. ed., Milano, Springer, 2006.
Quarteroni 2006: Complex systems in biomedicine, edited by Alfio Quarteroni, Luca Formaggia, Alessandro Veneziani, Milano, Springer, 2006.
Quarteroni 2008: Quarteroni, Alfio - Sacco, Riccardo - Saleri, Fausto, Matematica numerica, 3. ed., Milano, Springer, 2008.
Quarteroni, Formaggia 2004: Quarteroni, Alfio - Formaggia, Luca, Mathematical modelling and numerical simulation of the cardiovascular system, in: Handbook of numerical ana-lysis, XII, Computational models for the human body, edited by Nicholas Ayache, Amsterdam, Elsevier, 2004, pp. 1-101.
Quarteroni, Saleri 2006: Quarteroni, Alfio - Saleri, Fausto, Scientific computing with MATLAB and Octave, Berlin-Heidelberg, Springer, 2006.
Quarteroni, Valli 1999: Quarteroni, Alfio - Valli, Alberto, Domain decomposition methods for partial differential equations, Oxford, Oxford University Press, 1999.
Quarteroni, Saleri 2006: Quarteroni, Alfio - Saleri, Fausto, Introduzione al calcolo scientifico, Milano, Springer, 2006.