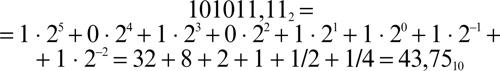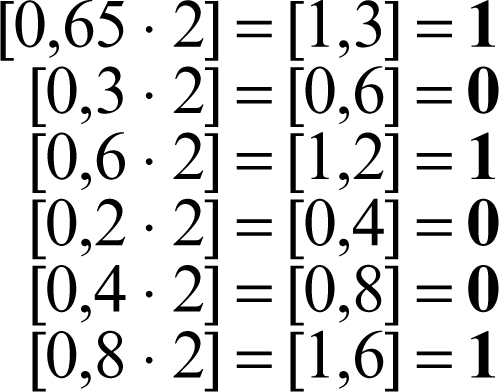sistema binario
sistema binario
sistema binario sistema di numerazione posizionale in base due; la base è generalmente indicata come pedice della sequenza delle cifre. In tale sistema, utilizzato per rappresentare i numeri in un elaboratore elettronico, essendo il bit il dato elementare registrabile su supporti elettronici a due stati, ci sono soltanto due cifre, 0 e 1 (→ aritmetica finita (di macchina)). Dato un numero binario, il suo corrispondente decimale si ottiene sviluppandolo secondo le potenze di 2. Per esempio:
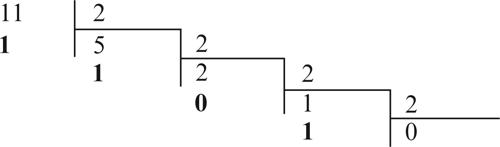
Viceversa, per la rappresentazione binaria (in base 2) del numero decimale 11,65 occorre seguire due diverse procedure per la parte intera e per quella decimale. Per la parte intera si considerano, in ordine inverso, i diversi resti nelle successive divisioni per 2 fino a che il quoziente è 0:
Si ha quindi 1110 = 10112. Per la parte decimale si considerano, nell’ordine in cui compaiono, le successive → parti intere, indicate con […], nelle moltiplicazioni per 2 delle parti decimali che via via si ottengono, fino a che il prodotto è 1 oppure fino a che non compare una moltiplicazione già considerata (il che significa che nel sistema binario il numero è periodico) oppure fino alla approssimazione voluta. Per ottenere la rappresentazione binaria di 0,6510 occorre quindi procedere nel seguente modo:
Qui il procedimento si arresta perché dalla successiva moltiplicazione (che sarebbe ancora [0,6 ⋅ 2]) le cifre si ripetono. Si ha perciò
in cui la parte sopra segnata indica il periodo. Complessivamente:
Come si può osservare dall’esempio, può accadere che un numero razionale abbia una rappresentazione finita in una base e infinita periodica in un’altra; i numeri irrazionali hanno invece, in qualunque base, una rappresentazione con infinite cifre decimali non periodiche. Queste procedure di trasformazione sono identiche per qualunque altra conversione da base decimale a una base b e viceversa (salvo considerare come divisore e moltiplicatore il numero b anziché 2). Per le conversioni tra due diverse basi non decimali possono esserci procedure più brevi. Per esempio, nel sistema in base 8, detto anche sistema di numerazione ottale, in cui le cifre sono {0, 1, …, 7} e i numeri sono rappresentati tramite le successive potenze di 8, la conversione da base 2 a base 8 e viceversa è facilitata dal fatto che 8 = 23 e quindi a ogni gruppo di 3 cifre in base 2 corrisponde una cifra in base 8. Così per esempio 11011112 = 001 101 1112 = 1578 = 1 ⋅ 82 + 5 ⋅ 81 + 7 ⋅ 80 = 11110.