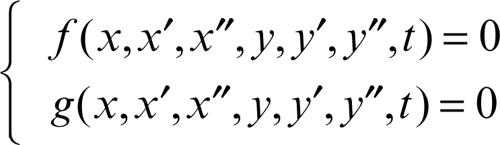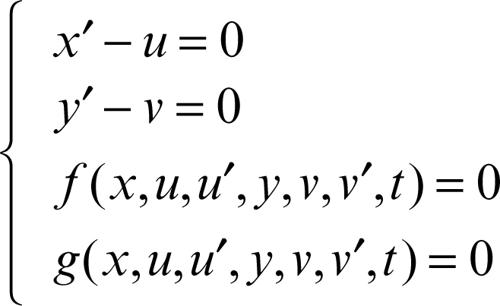sistema differenziale

sistema differenziale

sistema differenziale sistema di equazioni (o disequazioni) differenziali le cui soluzioni sono date dalle n-ple di funzioni che soddisfano tutte le formule differenziali che lo compongono. Un sistema di equazioni differenziali ordinarie può essere sempre scritto mediante equazioni del primo ordine, assegnando un nuovo nome a tutte le derivate di ordine minore del massimo. Per esempio, il sistema di due equazioni del secondo ordine

nelle incognite x(t), y(t), mediante la sostituzione x′ = u, y′ = ν si trasforma nel sistema

L’ordine del sistema è la somma degli ordini massimi con cui compaiono le incognite e quindi nell’esempio è 4. Se un sistema di equazioni differenziali è risolto rispetto alle derivate di ordine massimo, cioè esse compaiono isolate a primo membro nelle equazioni, esso si dice in forma normale e per esso vale il teorema di esistenza e unicità. Precisamente, se le incognite sono indicate con x_k(t), 1 ≤ k ≤ n, un sistema in forma normale assumerà la forma

Il problema di → Cauchy che si ottiene assegnando il dato iniziale

ammette una e una sola soluzione se le funzioni ƒ_k sono continue e soddisfano la condizione di → Lipschitz rispetto alle incognite x_k in un intorno del punto iniziale. Se tale condizione vale uniformemente per t in un intervallo [a, b], cioè se risulta

con L costante opportuna, per ogni coppia di punti (x₁, …, x_n) e (y₁, …, y_n) e per ogni t ∈ [a, b], la soluzione esiste in tutto [a, b]. L’integrale generale di un sistema differenziale di ordine n dipende da n costanti arbitrarie. In particolare ciò è assicurato per i sistemi lineari, aventi la forma

con A matrice dei coefficienti e b(t) vettore termine noto (o forzante) continui in un determinato intervallo e x(t) ∈ Rⁿ. Se b(t) = 0, il sistema si dice omogeneo; due sistemi si dicono associati se hanno la stessa matrice dei coefficienti.

Un sistema si dice autonomo se la variabile indipendente t non vi compare esplicitamente. Formalmente, ogni sistema può essere reso autonomo aumentando il numero delle incognite con la posizione x_n+1 = t, cui corrisponde l’equazione x′_n+1 = 1. Nei sistemi autonomi lineari la matrice A è costante. Se la matrice è diagonalizzabile (il che avviene se i suoi autovalori λ_k sono distinti, o se, più in generale, a un autovalore multiplo corrisponde un numero di autovettori linearmente indipendenti u_k uguale alla molteplicità algebrica dell’autovalore), l’integrale generale del sistema omogeneo è dato da

dove C_k sono costanti arbitrarie (→ matrice esponenziale; → matrici, serie di). Ciascuno dei termini e^λktu_k costituisce un modo fondamentale. Se A è reale, a una coppia di autovalori coniugati λ_k = α_k + i β_k, λ_k+1 = α_k − i β_k corrispondono autovettori a_k ± i b_k coniugati e la combinazione delle due soluzioni complesse può essere sostituita dalla combinazione reale

che è composta di modi fondamentali oscillanti (smorzati se α_k < 0). Se tutti gli autovalori hanno parti reali dello stesso segno, tutte le soluzioni ammettono lo stesso comportamento asintotico per t → +∞ (e il comportamento opposto per t → −∞). Per la discussione completa del caso bidimensionale si veda → sistema differenziale, stabilità di un. La parte corrispondente alla soluzione del sistema omogeneo corrisponde alla evoluzione libera, o propria, di un sistema; a questa, per ottenere l’evoluzione generale, va aggiunta la risposta forzata p(t) corrispondente al termine noto b(t), per il cui calcolo si rinvia a → matrice wronskiana. Nel caso in cui gli autovalori abbiano parte reale negativa, il contributo dovuto all’integrale generale del sistema omogeneo associato (che contiene, attraverso le costanti, le informazioni relative al problema di Cauchy, cioè ai valori iniziali), è smorzato esponenzialmente e corrisponde dunque al termine transitorio, mentre la soluzione forzata fornisce il termine di regime, o permanente, del sistema.