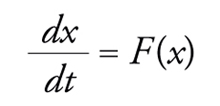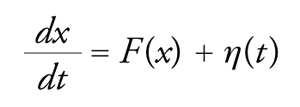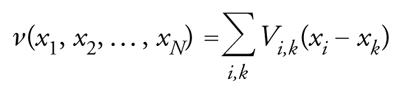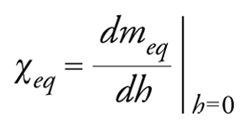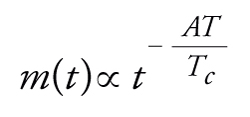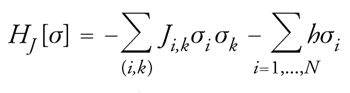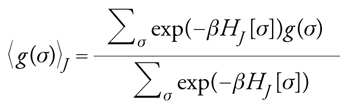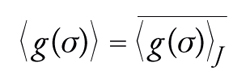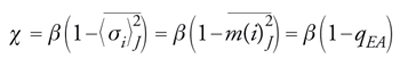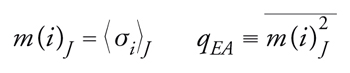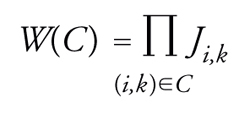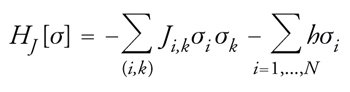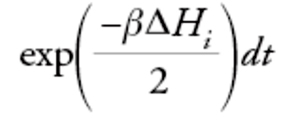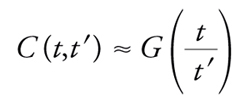Sistemi complessi, fisica dei

Sistemi complessi, fisica dei

Lo studio dei sistemi complessi è un campo nuovo, che si caratterizza, fra l'altro, per la sua natura altamente interdisciplinare: basti pensare alle connessioni con la biologia, l'informatica, la teoria dei sistemi, la finanza e l'ecologia. Lo stesso termine 'complesso' sembra scivolare tra le mani di chi cerchi di darne una definizione precisa: a volte è usato nel senso di complicato, cioè composto da molti elementi (una centrale nucleare è un sistema complesso, in quanto composto da migliaia di pezzi differenti); altre volte la sua connotazione è piuttosto quella di imprevedibile (l'atmosfera è un sistema complesso, in quanto non può essere oggetto di previsioni a lunga scadenza). Dal punto di vista di un fisico, l'obiettivo da raggiungere consiste nel trovare le leggi macroscopiche, dette fenomenologiche, che regolano il comportamento globale di tali sistemi, e che non sono facilmente deducibili dall'analisi delle leggi microscopiche che controllano ciascuno dei singoli costituenti. Facciamo un esempio: il comportamento dei singoli neuroni è probabilmente ben compreso, ma non ci è affatto chiaro perché dieci miliardi di neuroni, collegati da centomila miliardi di sinapsi, formino un cervello che è in grado di pensare come quello dei primati. In certi contesti la comparsa di comportamenti collettivi è un fenomeno ben studiato dalla fisica: la cooperazione di molti atomi e molecole è responsabile delle transizioni di fase (tipo liquido-solido o liquido-gas).

Quando un sistema presenta più di una fase, possiamo descriverlo dal punto di vista macroscopico specificando in quale fase esso si trovi (per es., solida, gassosa o liquida). Nei sistemi fisici, a una data temperatura e a una data pressione il numero delle fasi è di norma piccolo: l'acqua può stare in uno, due o al massimo tre stati di aggregazione, se si considera anche il punto triplo, dove solido, liquido e gas coesistono. La descrizione macroscopica è assai semplice e può essere fatta con un linguaggio molto povero. Al contrario, se esaminiamo un sistema biologico, che possiamo considerare come il prototipo di un sistema complesso, la sua descrizione macroscopica può essere molto varia e richiedere un linguaggio con un vocabolario assai ricco (un animale può correre, mangiare, dormire, saltare, ecc.). La varietà delle descrizioni macroscopiche può essere presa come indicatore di complessità. Una proprietà fondamentale dei sistemi complessi è quindi la possibilità di essere descritti sia a livello microscopico, sia a un livello più alto in cui bisogna usare categorie e concetti diversi.

Da questo punto di vista, tutti i sistemi fisici tradizionali sono semplici e la complessità, tradizionalmente, era esclusa dal mondo della fisica. In questi ultimi anni la situazione è cambiata: sono stati individuati numerosi sistemi caratterizzati da aggregazioni molecolari disordinate, per i quali la descrizione macroscopica è molto ricca. Ne è un esempio un eteropolimero, vale a dire un polimero composto da una sequenza di molecole differenti. Le proteine, il DNA e l'RNA sono eteropolimeri che hanno un ruolo importantissimo nella biologia. Altri sistemi fisici che hanno proprietà simili, come i vetri di spin, sono stati studiati attentamente e la struttura delle differenti fasi è stata calcolata in dettaglio. Questi risultati, che mostrano l'esistenza di sistemi fisici relativamente semplici con una descrizione macroscopica complessa, permettono di intraprendere la costruzione di una teoria fisica della complessità.

La maggior parte di tali sistemi ha un comportamento caotico molto interessante: un piccolo cambiamento nella forma delle leggi che ne regolano il movimento ne cambia completamente il comportamento macroscopico. Il fenomeno è ben noto in biologia: la sostituzione di un singolo amminoacido in una proteina può alterarne la funzionalità, una singola mutazione in un essere vivente può portare alla comparsa di una nuova specie o alla morte. Molto spesso lo studio dei sistemi complessi è stato portato avanti sia analiticamente, sia effettuando simulazioni numeriche utilizzando calcolatori; i vantaggi dei due approcci si combinano sinergicamente, poiché i calcolatori permettono di effettuare simulazioni di sistemi di complessità crescente, in maniera da ricavare leggi quantitative e qualitative da sistemi di complessità moderata, prima di cimentarsi con sistemi veramente complessi. L'analisi in parallelo dei risultati analitici ottenuti su sistemi più semplici e delle simulazioni numeriche di sistemi di complessità intermedia, sembra essere una metodologia molto efficace che ha permesso di compiere notevoli progressi.

Il prototipo di un sistema complesso

fig. 1

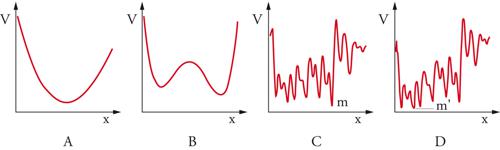
Il più semplice esempio di sistema complesso è rappresentato da una singola particella che può muoversi interagendo con un potenziale dotato di numerosi massimi e minimi. Consideriamo, per esempio, il caso di una particella immersa in un fluido viscoso, che si muova in una dimensione subendo l'effetto della forza generata dai potenziali disegnati nella fig. 1. L'equazione del moto della particella è, nel limite di alta viscosità e trascurando l'inerzia,

[1] formula

dove la forza F(x) è proporzionale al gradiente del potenziale (F(x)=−C dV/dx) e la costante C è inversamente proporzionale alla viscosità. L'evoluzione temporale è tale da portare la particella nei minimi del potenziale. La particella, lasciata a se stessa, raggiungerà in tempi più o meno lunghi il minimo, se esso è unico (fig. 1A). Nel caso di due minimi (fig. 1B), dopo un tempo lungo la particella sarà vicina a uno dei due, ma la scelta del minimo dipenderà dalle condizioni iniziali; con un potenziale in cui i minimi sono numerosi (fig. 1C), la particella andrà vicino a uno di questi. Per descrivere lo stato della particella in tempi lunghi dobbiamo specificare vicino a quale minimo (fig. 1D) essa si trovi.

Si può arricchire il modello supponendo che la particella sia molto piccola, per esempio visibile all'ultramicroscopio, e che quindi, come nel caso del moto browniano, risenta dell'agitazione termica delle molecole. Per descrivere questa situazione si deve aggiungere un termine casuale alle equazioni del moto e scrivere l'equazione di Langevin,

[2] formula

dove η(t) è una forza fluttuante al variare del tempo (tecnicamente, un 'rumore bianco'), con varianza proporzionale alla temperatura; più precisamente abbiamo che η(t)η(t′)=2Tδ(t−t′), dove la barra indica la media sul rumore. La presenza del rumore permette alla particella di risalire il potenziale e di passare da un minimo a un altro. Questo processo può essere anche estremamente lento, in quanto il tempo necessario per passare spontaneamente da un minimo a un altro è esponenzialmente grande: a basse temperature è dato da

[3] exp(βΔV)

dove β=1/kT (essendo k la costante di Boltzmann e T la temperatura assoluta) e ΔV è la barriera di potenziale da attraversare. Se la temperatura è sufficientemente bassa (β è quindi elevato) e al tempo zero la nostra particella parte da un punto scelto casualmente, possiamo distinguere tre fasi nella sua dinamica: (a) la particella si muove verso il minimo locale più vicino, come nel caso a temperatura zero; (b) la particella salta da un minimo locale a un altro, muovendosi in media verso minimi locali con energia sempre minore; (c) la particella ha fatto un gran numero di salti e ha raggiunto il minimo assoluto del potenziale. In quest'ultima fase, la particella frequenta ciascuno dei minimi locali con una probabilità proporzionale a exp(−βV(x)). Se la differenza di energia tra il minimo assoluto e i minimi locali è elevata, la particella starà quasi sempre vicino al minimo assoluto; se al contrario vi sono minimi locali con energia paragonabile a quella del minimo assoluto, essi saranno frequentati con una probabilità elevata. In tal caso i vari minimi locali corrispondono ai vari stati di equilibrio del sistema.

La complessità della forma del potenziale si riflette quindi nella complessità del comportamento del sistema. La descrizione mediante un potenziale con molti minimi e massimi può risultare artificiosa nel caso di una singola particella, ma se consideriamo un sistema formato da molte particelle che interagiscono fra loro a coppie, il potenziale totale dipende dalla somma dei potenziali delle singole coppie,

[4] formula,

dove le variabili x_i, essendo i=1,...,N, sono le coordinate delle N particelle e V_i,k(x_i−x_k) è il potenziale tra l'i-esima e la k-esima particella: si può dimostrare che in molti casi il potenziale globale ν ha numerosissimi minimi per N grande (a volte il loro numero diverge esponenzialmente con N), anche se i singoli potenziali V_i,k(x) hanno un solo minimo. La complessità del sistema nasce naturalmente dall'interazione tra molti sistemi semplici.

I sistemi amorfi

Un sistema formato da atomi di una o più specie chimiche può trovarsi in uno stato solido, liquido o gassoso. Nel caso dello stato solido, dobbiamo distinguere ancora due possibilità: il solido regolare e il solido amorfo. Se si tratta di un solido regolare, gli atomi formano un cristallo e sono localizzati attorno a posizioni fisse del reticolo cristallino; nel caso in cui sia costituito da due o più specie chimiche, un cristallo regolare si può formare solamente quando queste sono in precise proporzioni. L'amorfo può essere considerato come un liquido congelato: gli atomi sono in posizioni disordinate, come in un liquido, ma non possono allontanarsi dalla posizione che hanno assunto al momento della formazione dell'amorfo, in quanto la densità, (di regola) maggiore rispetto a quella di un liquido, e l'agitazione termica, minore, ne impediscono il movimento. Gli esempi più comuni di materiali amorfi sono il vetro, la cera e, più in generale, le leghe in cui i diversi elementi sono disposti microscopicamente in maniera casuale.

A volte gli amorfi non sono stati stabili, ma metastabili: se si aspetta un tempo sufficientemente lungo (per es., dell'ordine dell'età dell'Universo), le rarissime fluttuazioni termiche, che sono in grado di spostare gli atomi, riconducono il sistema in uno stato regolare. La distinzione tra stati amorfi stabili e metastabili è importante per comprendere la dinamica della formazione dei sistemi amorfi, ma è irrilevante per quanto concerne la descrizione della fase amorfa a bassa temperatura, su scale di tempi paragonabili a quelli della vita umana. Possiamo quindi ritenere a tutti gli effetti che le posizioni di equilibrio degli atomi di un sistema amorfo siano congelate e che gli atomi compiano soltanto piccole oscillazioni rispetto alla posizione d'equilibrio. La forma di queste oscillazioni dipende dal modo in cui gli atomi si sono posizionati al momento del loro congelamento. Se escludiamo la possibilità di riscaldare nuovamente il sistema e consideriamo come gradi di libertà solamente le piccole oscillazioni, le leggi che le governano, e in particolare l'espressione della loro energia, dipendono dal modo casuale in cui gli atomi si sono disposti al momento della formazione dell'amorfo. Le piccole oscillazioni intorno alla posizione d'equilibrio formano un sistema intrinsecamente disordinato, in cui le leggi stesse del moto sono scelte in maniera casuale. Nel caso degli amorfi, si tratta di un fenomeno generale. Gli atomi si dispongono casualmente quando l'amorfo è ottenuto raffreddando il liquido. Una volta che l'amorfo si è formato, le componenti del sistema che non sono congelate sono soggette a forze (per es., le oscillazioni degli atomi e le interazioni degli elettroni, nel caso delle leghe metalliche o dei semiconduttori) la cui espressione matematica è scelta in maniera casuale tra le tante possibili.

Nello studio dei sistemi intrinsecamente disordinati è necessario capire quali sono le proprietà del sistema che dipendono dalla sua realizzazione fisica e quali le proprietà che, nel caso di sistemi macroscopici, non dipendono da tale realizzazione. Consideriamo per esempio due campioni di vetro con la medesima composizione chimica: se procediamo alla loro preparazione utilizzando lo stesso protocollo, le posizioni dei singoli atomi risultano differenti, ma ci aspettiamo, come l'esperimento conferma, che la conducibilità termica e altre proprietà fisiche siano le stesse. Sebbene la conducibilità termica dei due campioni sia localmente diversa e dipenda dalla disposizione degli atomi in quel determinato punto, in tutto il campione le differenze sono molto piccole ed estremamente difficili da osservare, perché nel caso di un sistema macroscopico le fluttuazioni locali si compensano. Se invece facciamo cadere i due campioni di vetro per terra, essi, anche se procediamo il più possibile nello stesso modo, si frattureranno diversamente, in pezzi più o meno grandi e dalle forme più varie. La linea di frattura segue infatti la disposizione dei singoli legami più deboli e, in questo caso, la diversa disposizione degli atomi ha un effetto macroscopico sul sistema, cosicché il risultato dell'esperimento dipende dalla scelta del campione. Sarà dunque compito della teoria discriminare le proprietà che dipendono dalla disposizione microscopica degli atomi da quelle che ne sono indipendenti. Lo studio teorico degli amorfi non deve essere fatto su un singolo sistema; bisogna considerare simultaneamente una classe di sistemi che differiscano gli uni dagli altri per una componente casuale. In molti casi il disordine, ossia la presenza di termini casuali nel determinare la forma dell'energia, non produce effetti qualitativamente importanti; in altri casi il disordine induce proprietà del tutto nuove e il sistema può essere classificato come complesso.

I vetri di spin

I vetri di spin, detti anche magneti amorfi, sono tra i più studiati sistemi fisici in cui il disordine induce nuovi effetti. Questi materiali, per lo più leghe metalliche, hanno un comportamento magnetico anomalo a basse temperature e non rientrano nella consueta classificazione che, in base alle proprietà magnetiche, distingue i materiali in ferromagnetici, antiferromagnetici, e così via. In fisica, i vetri di spin sono il prototipo di un sistema complesso.

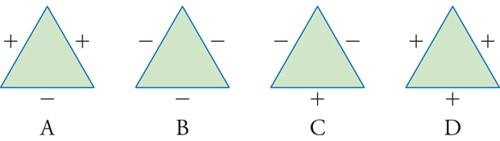
Considerazioni generali

Prima di entrare nei dettagli delle proprietà, è opportuno presentare alcune considerazioni generali e un esempio familiare. Supponiamo che in una stanza vi sia un certo numero di persone che si conoscono, divise a caso in due gruppi, e che successivamente venga domandato a ciascuna se vuole passare da un gruppo all'altro (ogni interpellato risponderà sì o no a seconda delle proprie simpatie o antipatie); in caso di risposta positiva, la persona cambia immediatamente gruppo. Dopo un primo giro, non tutti saranno ancora soddisfatti: qualcuno che aveva cambiato di posto (o che non si era spostato al primo giro), vorrà riconsiderare la propria situazione dopo i cambiamenti effettuati dagli altri. Si procede a un secondo giro di spostamenti e si va avanti così, finché non vi è più alcuno che richieda di cambiare di posto. A uno stadio successivo, possiamo provare a spostare non soltanto i singoli, ma anche più persone contemporaneamente (può capitare, infatti, che un cambiamento di gruppo sia vantaggioso solamente se fatto in compagnia), finché non si raggiunge uno stato di soddisfazione generale.

La possibilità di accogliere tutte le richieste dei singoli dopo un numero finito di giri dipende crucialmente dall'ipotesi che la relazione di simpatia sia simmetrica, ossia che, se Tizio è simpatico a Caio, anche Caio sia simpatico a Tizio. Possono però presentarsi anche situazioni asimmetriche: Tizio ha simpatia per Caio, ma Caio non può sopportare Tizio. Nel caso in cui situazioni di questo tipo siano molto comuni, il procedimento sopra indicato non tenderà mai a uno stato stabile: Tizio insegue Caio che scappa e i due non si fermeranno mai. Il caso in cui il rapporto è asimmetrico differisce profondamente da quello in cui esso è simmetrico; soltanto in questo secondo caso le volontà dei singoli sono tutte orientate verso lo stesso scopo di ottimizzazione della soddisfazione generale. La configurazione finale dipenderà ovviamente dai sentimenti reciproci e dalla configurazione iniziale e, quindi, non è direttamente calcolabile in assenza di tali informazioni.

Possiamo tuttavia pensare di calcolare approssimativamente alcune proprietà generali di questa dinamica, per esempio quanti giri siano necessari affinché tutti risultino soddisfatti, nell'ipotesi che la distribuzione delle simpatie e delle antipatie sia casuale. Supponiamo di conoscere la distribuzione di probabilità delle simpatie, ipotizzando, per esempio, che la probabilità che due persone scelte casualmente si siano simpatiche sia p, dove p è un numero compreso fra 0 e 1 (spesso si considera il caso p=1/2). Bisogna poi verificare se questa modellizzazione dei rapporti sia corretta o se invece la situazione reale non sia più complicata: per esempio, possiamo introdurre una gradazione nell'antipatia e supporre che i vicini di casa abbiano rapporti molto intensi, mentre persone che abitano lontano si siano praticamente indifferenti. Una volta ottenuta una modellizzazione accurata della distribuzione di probabilità delle simpatie, possiamo cercare di fare previsioni sul sistema, che saranno di natura puramente probabilistica e diventeranno tanto più precise (ossia con un errore relativo sempre più piccolo) quanto più il sistema diventerà grande (ossia nel limite in cui il numero dei componenti tende a infinito).

Il sistema descritto nel caso simmetrico corrisponde puntualmente (in termini matematici) ai vetri di spin: se sostituiamo le parole 'simpatico' e 'antipatico' con 'ferromagnetico' e 'antiferromagnetico' e identifichiamo i membri dei due gruppi con spin orientati in direzioni differenti, otteniamo una descrizione precisa dei vetri di spin. A basse temperature, infatti, un sistema fisico si evolve in maniera tale da minimizzare l'energia e questa dinamica è molto simile al processo di ottimizzazione appena descritto, a patto di identificare l'energia con l'insoddisfazione generale. I vetri di spin sono stati ampiamente studiati e siamo attualmente in grado di rispondere a molte delle domande che erano state poste al riguardo. Le caratteristiche forse più interessanti di questi sistemi, sono costituite dall'esistenza di un gran numero di stati di equilibrio differenti (se spostiamo una sola persona alla volta) e dalla grande difficoltà a trovare la configurazione ottimale al variare di un numero arbitrariamente grande di elementi.

I vetri di spin sono infatti uno degli esempi più noti di quei problemi di ottimizzazione (detti NP completi, per motivi che non vale la pena discutere in questa sede), la cui soluzione può essere trovata soltanto mediante un numero di passi estremamente elevato, crescente esponenzialmente con il numero degli elementi del sistema. La presenza di un gran numero di diversi stati di equilibrio può essere considerata come una delle caratteristiche più tipiche dei sistemi complessi (almeno in una delle tante accezioni del termine): ciò che non si può modificare con il tempo non è complesso, mentre un sistema che può assumere molte forme diverse è certamente complesso. Una scoperta inattesa è stata che la complessità emerge naturalmente dal disordine delle leggi del moto. Per ottenere un sistema complesso non dobbiamo sforzarci di scegliere leggi molto particolari: basta sceglierle a caso, ma con distribuzioni di probabilità ben determinate.

I vetri di spin reali

I vetri di spin sono materiali magnetici in cui l'interazione fra coppie di spin è a volte ferromagnetica e a volte antiferromagnetica. Il caso più semplice è dato da vetri di spin sostituzionali costituiti da un composto terziario. Il 50% degli atomi appartiene a una sostanza magnetica (che indichiamo con M), mentre l'altro 50% appartiene a due sostanze non magnetiche in proporzione fissa (che indichiamo con A e B). Per certi tipi di materiale gli atomi M si dispongono su un reticolo cubico, mentre gli atomi delle sostanze non magnetiche sono situati al centro dei segmenti che congiungono gli atomi magnetici. Se le proprietà stereochimiche delle due sostanze non magnetiche sono relativamente simili, al momento della formazione del composto cristallino la posizione degli atomi delle sostanze non magnetiche sarà del tutto casuale. La disposizione spaziale degli atomi non magnetici ha conseguenze importantissime sulle proprietà magnetiche. La forza, che provoca l'ordinamento degli atomi magnetici nei normali ferromagneti, infatti, è proporzionale alla sovrapposizione delle funzioni d'onda e perciò agisce soltanto tra atomi vicini. Nel caso del composto che stiamo considerando, gli atomi magnetici sono molto distanti tra loro e quindi, in prima approssimazione, non interagiscono. Rimane però un'interazione residua, che è dovuta alla presenza degli altri atomi e che dipende crucialmente dal tipo di atomo: se l'atomo intermedio è A, l'interazione (ferromagnetica) tra i dipoli magnetici dei due atomi è tale da orientarli nello stesso verso; se invece l'atomo intermedio è B, l'interazione (antiferromagnetica) è tale da orientare i due atomi in versi opposti. Al variare della percentuale x di atomi di A (la percentuale di B sarà quindi 50−x), passiamo da un caso di ferromagnetismo perfetto (x=50) a un sistema antiferromagnetico (x=0). Per x=25 le interazioni sono casualmente ferromagnetiche o antiferromagnetiche e quindi otteniamo il modello descritto in precedenza, in cui soltanto i vicini di casa nutrono antipatia o simpatia reciproche.

fig. 2

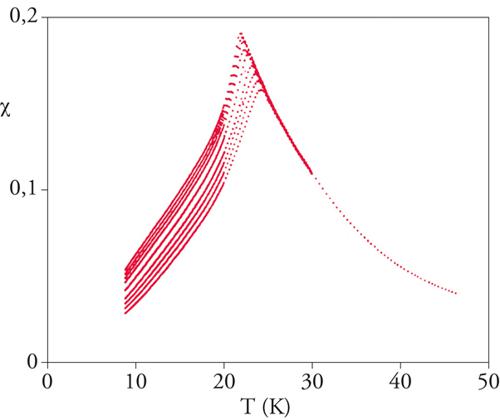
I vetri di spin sono stati ampiamente studiati in ambito sperimentale. Assai interessante si è rivelato il comportamento della suscettività magnetica χ. Conviene introdurre una suscettività magnetica χ=χ(ω), dipendente dalla frequenza e proporzionale alla magnetizzazione di un sistema sottoposto a un piccolo (infinitesimo) campo magnetico alternato di frequenza ω; in altri termini, la quantità χ(ω) è la risposta lineare del sistema a un campo magnetico alternato e per un sistema normale, nel limite di basse frequenze (ω che va a zero), χ(ω) diventa l'usuale suscettività statica. Nella fig. 2 possiamo vedere l'andamento della suscettività χ(ω) in funzione della temperatura, per diversi valori della frequenza. Nella zonadi alta temperatura i risultati sono indipendenti dallafrequenza; nella zona di bassa temperatura si osserva invece una forte dipendenza da ω, anche nella regione in cui le oscillazioni del campo magnetico hanno un periodo di un minuto, tempo enormemente più grande rispetto a quello necessario per rovesciare un singolo spin (10⁻¹² s): i processi collettivi attraverso i quali la magnetizzazione cambia al variare del campo magnetico diventano lentissimi a basse temperature.

Una delle caratteristiche più salienti dell'andamento in esame è la presenza di un picco ben pronunciato, che si sposta verso le temperature più basse al diminuire della frequenza. Sebbene lo spostamento del picco sia contenuto, esso risulta circa della medesima entità ogni qualvolta si diminuisca la frequenza di un fattore dieci. L'estrapolazione a frequenza zero è molto difficile e può essere fatta soltanto basandosi su ipotesi al momento attuale non completamente certe. Indichiamo con χ_R il valore della suscettività misurata su una scala di tempo macroscopica (ossia a una frequenza dell'ordine di 1 Hz): il valore di χ_R cambia molto poco, quando cambiamo la scala di tempo su cui misuriamo la suscettività da un secondo a un'ora.

Una definizione differente di suscettività può essere ottenuta raffreddando il campione in presenza di un campo magnetico h e misurando la magnetizzazione m(h). La magnetizzazione misurata con questa tecnica dipende assai poco dalla velocità con cui il sistema è raffreddato; per tale motivo si ritiene comunemente che essa sia molto vicina al valore m_eq(h) che dovrebbe assumere all'equilibrio termico. Nello stesso modo si può definire lasuscettività magnetica raffreddata sottocampo (fieldcooling), per esempio a h=0, come

[5] formula.

fig. 3

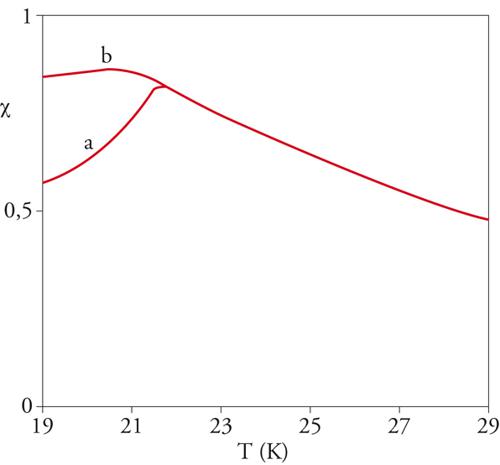
La suscettività χ_eq ha il comportamento illustrato nella fig. 3. Ad alte temperature essa coincide con χ_R, ma a basse temperature diventa circa costante, al contrario di χ_R, che diminuisce notevolmente con la temperatura (fig. 2). La differenza fra le due suscettività è connessa alla presenza di fenomeni di isteresi magnetica. Se si raffredda il sistema in presenza di un campo magnetico e successivamente si rimuove il campo, la magnetizzazione del sistema non scompare velocemente, ma rimane diversa da zero e decresce molto lentamente con lo scorrere del tempo (magnetizzazione residua). Al contrario, la magnetizzazione m_eq(h) è praticamente indipendente dal tempo. La dipendenza dal tempo della magnetizzazione residua è varia ed è influenzata da molti parametri, quali l'ampiezza della variazione del campo magnetico e il tempo in cui il sistema è rimasto a bassa temperatura prima di rimuovere il campo magnetico.

Per brevità, consideriamo soltanto il caso in cui la variazione del campo magnetico è grande: sperimentalmente, si trova che la magnetizzazione residua m(t) decade approssimativamente come

[6] formula.

In questa formula (valida per T〈T_c) A è circa 0,3 e T_c è la temperatura a cui la suscettività alternata a basse frequenze ha un picco (per es., ca. 21 K nel caso del materiale nelle figg. 2 e 3). Essa implica un decadimento molto lento della magnetizzazione residua. Per esempio, a una temperatura uguale a un terzo di T_c la magnetizzazione decade come t⁻¹: questo comportamento, anche per un grande intervallo di tempo di misurazione, non è facilmente distinguibile da una dipendenza logaritmica, ossia m(t)=m₀−m₁ln(t), dove m₀ e m₁ sono costanti opportune. Diversamente da altre transizioni di fase, il calore specifico non mostra anomalie degne di nota. Si osserva solamente un massimo molto largo a una temperatura di circa il 50% più alta di T_c. Alcune di queste caratteristiche peculiari dei vetri di spin possono essere ben spiegate dalla teoria.

Un modello microscopico

Per descrivere i vetri di spin sostituzionali si può ricorrere a un modello molto semplice. Gli spin, localizzati sugli atomi magnetici, sono schematizzati come variabili a due valori definite sui nodi di un reticolo regolare; anche le costanti d'accoppiamento possono avere due valori e sono definite sui legami dello stesso reticolo. Il sistema è dunque descritto da N variabili σ_i (dove i varia da 1 a N), che possono assumere i valori 1 oppure −1 e che corrispondono agli spin; per ogni possibile coppia di punti primi vicini (i,k), è introdotta una variabile J_i,k che è scelta casualmente e ha valore 1 o −1 con uguale probabilità. L'energia H_J[σ] è data dalla somma su tutte le coppie (i,k) di J_i,kσ_iσ_k più il contributo magnetico,

[7] formula,

dove la prima somma è ristretta solamente alle coppie di punti primi vicini. Il campo magnetico esterno, h, tende a far assumere agli spin il suo stesso segno. Per il momento ci limitiamo a considerare il caso h=0. Se J_i,k è positivo, la minimizzazione del contributo della coppia (i,k) all'energia H si ottiene scegliendo gli stessi valori per i due spin σ_i e σ_k. Le variabili J sono casuali e indipendenti l'una dall'altra. Per ogni scelta delle variabili J possiamo definire un valore medio statistico,

[8] formula,

dove g(σ) è una funzione generica di σ.

Per ipotesi la distribuzione di probabilità delle variabili J non è alterata dalla loro interazione con gli spin σ. Si tratta di un'approssimazione molto buona, in quanto l'interazione magnetica è rilevante soltanto a temperature molto più basse della temperatura di fusione del composto metallico e può essere quindi trascurata durante la formazione della lega. Quando l'interazione magnetica diventa importante (a una temperatura di qualche decina di kelvin), gli atomi possono solamente oscillare intorno alla loro posizione di equilibrio e non possono più cambiare posizione. Se durante la preparazione del campione la temperatura viene diminuita abbastanza rapidamente, la posizione degli atomi non è minimamente influenzata dalla loro interazione magnetica e le variabili possono essere considerate a buon diritto indipendenti le une dalle altre. Questo tipo di disordine è spesso chiamato congelato. A ogni campione differente corrisponde una scelta diversa delle variabili J. Se le quantità termodinamiche intensive, come la magnetizzazione e l'energia interna per unità di volume, dipendessero dalla scelta del campione, la situazione sarebbe imbarazzante, in quanto campioni preparati con lo stesso procedimento avrebbero proprietà differenti. Fortunatamente, è possibile dimostrare che per campioni abbastanza grandi le proprietà termodinamiche non dipendono dalla scelta del campione.

Per calcolare le proprietà del sistema è necessario stimare il valore medio 〈g(σ)〉_J per una scelta generica delle variabili J. Dato che questa quantità non varia troppo bruscamente al variare delle J, possiamo limitarci a calcolare

[9] formula,

dove abbiamo indicato con una linea orizzontale la media sulle variabili J. Una quantità molto interessante è la suscettività magnetica. Se si utilizza il formalismo usuale della meccanica statistica per la risposta alle piccole perturbazioni, si ottiene:

[10] formula,

dove

[11] formula;

m(i)_J è la magnetizzazione, che dipende dal nodo del reticolo, e q_EA è il cosiddetto parametro d'ordine di Edwards e Anderson. La formula precedente non può essere esatta a basse temperature, in quanto non fa distinzione fra le varie suscettività che abbiamo introdotto in precedenza: la teoria della risposta lineare a piccole perturbazioni non si può applicare in questo caso e vedremo in un secondo tempo come procedere in modo corretto. Semplici argomenti fisici implicano che ad alte temperature e a campo magnetico esterno h uguale a zero, non vi sia magnetizzazione spontanea e di conseguenza q_EA=0. A basse temperature, ogni campione sviluppa la propria magnetizzazione spontanea (la magnetizzazione m_i varia da punto a punto e da campione a campione) e di conseguenza q_EA≠0 in questa regione. La transizione di fase vetrosa è caratterizzata da un valore di q_EA diverso da zero.

fig. 4

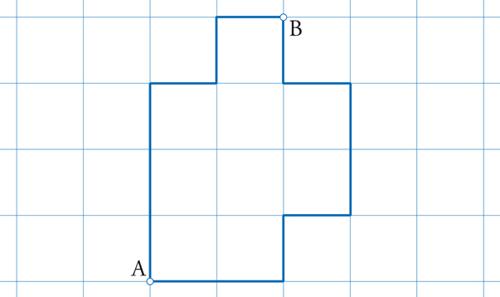
Un concetto molto importante nell'analisi teorica dei vetri di spin è dato dalla frustrazione, che si introduce nel seguente modo: associamo a un circuito chiuso sul reticolo (C) il prodotto W(C) di tutti i legami del circuito (fig. 4). Possiamo quindi definire:

[12] formula.

5

6

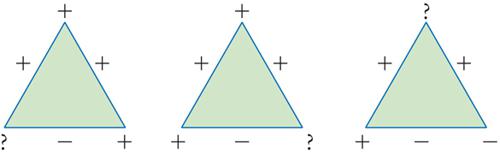
La quantità W(C) assume i valori ±1. Se W(C)=−1, il circuito è detto frustrato poiché non è possibile trovare un insieme di spin tali che J_i,kσ_iσ_k sia uguale a 1 per tutti i legami che appartengono al circuito. Il caso più semplice di un circuito frustrato è composto da tre spin (figg. 5 e 6) dove: due legami sono ferromagnetici e uno è antiferromagnetico. È evidente che non è possibile trovare tre spin tali da rendere uguali a 1 tutti i contributi all'energia. In generale, se esistono circuiti frustrati, devono anche esserci difetti, ossia legami che danno un contributo positivo all'energia. La frustrazione è molto importante, in quanto la sua presenza fa sì che il calcolo della configurazione di energia più bassa non sia banale.

Anche se il modello di Edwards e Anderson è una schematizzazione molto semplificata dei vetri di spin sostituzionali, tuttavia è possibile verificare che esso tiene conto delle caratteristiche salienti di tali sistemi. Simulazioni numeriche hanno dimostrato che tutti i fenomeni caratteristici osservati sperimentalmente nei vetri di spin sono riprodotti fedelmente da questo modello, che può essere quindi considerato un ottimo punto di partenza. L'interesse per questo modello nasce anche dal fatto che il comportamento della suscettività magnetica e quello della magnetizzazione residua, riscontrati nei dati sperimentali, si osservano, anche in questo caso semplificato, indicando che la stessa spiegazione teorica si possa applicare a entrambi i casi.

Un modello risolubile

Il precedente modello di Edwards e Anderson è molto difficile da studiare direttamente. La maggior parte dei progressi teorici è scaturita dallo studio di un modello semplificato, introdotto da David Sherrington e Scott Kirkpatrick. La forma dell'energia è identica a quella di un vetro di spin [7]:

[13] formula.

I due modelli sono differenti, in quanto in questo caso la somma è calcolata su tutte le possibili coppie (i,k), non è cioè limitata ai primi vicini, e la variabile J_i,k assume i valori ±N^−1/2. La scelta della normalizzazione delle costanti J è tale che la densità di energia E[σ]=H_J[σ]/N ha un limite finito quando N tende a infinito. Questo modello è piuttosto semplice da essere risolubile con precisione: per esempio, è possibile calcolare esattamente la densità di energia minima. In generale, scelte differenti delle variabili J_i,k corrispondono a sistemi con energie diverse. La teoria fornisce stime precise sul comportamento dei sistemi nel limite in cui N tende a infinito. Molte proprietà diventano infatti indipendenti dalla scelta delle variabili J e sono le stesse in pratica, per tutte le realizzazioni del sistema. In particolare, la densità di energia minima del sistema (il valore minimo di E[σ]) è uguale a circa −0,7633.

Il processo di minimizzazione successiva prima descritto corrisponde a scegliere sequenzialmente, per ogni i, la variabile σ_i in modo da minimizzare il suo contributo all'energia. Si può dimostrare che, se si parte da una configurazione casuale, si arriva a una densità di energia finale uguale a circa −0,73 e quindi decisamente più grande della minima. Un procedimento di ricerca sequenziale del minimo, una variabile dopo l'altra, non porta quindi al minimo globale, ma semplicemente a un minimo locale, ossia a una configurazione la cui energia non diminuisce cambiando un singolo spin alla volta. Il fatto che l'evoluzione del sistema si blocchi in un minimo locale è connesso all'esistenza di un numero elevatissimo di minimi locali. Il numero totale di minimi locali differenti aumenta circa come 20^0,30N (si tratta di un aumento esponenziale esattamente come per il numero totale di configurazioni, che aumenta come 2^N).

Il calcolo analitico dell'energia minima non è affatto semplice e può essere condotto utilizzando il metodo delle repliche, che si basa su alcune ipotesi che, pur essendo molto ragionevoli, non sono dimostrate in maniera completamente rigorosa. Se si segue questa strada, per valutare l'energia minima è necessario calcolare contemporaneamente il numero delle configurazioni con energia vicina a quella del minimo e le correlazioni esistenti tra la differenza in energia e la distanza fra due configurazioni, definita come la percentuale di spin differenti. Le configurazioni con energia vicina alla minima possono essere classificate secondo una struttura ad albero, simile a quelle utilizzate in biologia. Questo risultato, del tutto inaspettato, è molto interessante, in quanto mostra la grande ricchezza e complessità di un sistema apparentemente così semplice. L'interesse per il modello di Sherrington e Kirkpatrick nasce anche dal fatto che il comportamento della suscettività magnetica e quello della magnetizzazione residua, riscontrati nei dati sperimentali, si osservano anche in questo caso semplificato; ciò sembra indicare che la stessa spiegazione teorica si possa applicare a entrambi i casi.

Dinamica dei sistemi complessi

Finora abbiamo considerato le proprietà all'equilibrio e non abbiamo studiato l'evoluzione temporale. Dato che prendiamo in esame sistemi che non sono isolati, ma interagiscono con un bagno termico, è opportuno esaminare le equazioni del moto in cui si tiene conto in maniera esplicita delle fluttuazioni termiche. Quando il sistema è descritto da variabili continue, un'approssimazione molto buona è fornita dalla [2] (di Langevin). Se sono presenti gradi di libertà discreti, per i quali non è possibile scrivere un'equazione di Langevin, molto spesso si suppone che il sistema si evolva secondo una dinamica di Glauber: la probabilità di rovesciare lo spin σ_i in un intervallo di tempo infinitesimo dt è data da

[14] formula,

dove ΔH_i è la variazione d'energia prodotta da questo cambiamento. Per entrambe le dinamiche si può dimostrare che per un sistema finito la distribuzione di probabilità tende a quella di equilibrio quando il tempo tende a infinito.

Lo studio della dipendenza dal tempo delle proprietà di un sistema complesso, in particolare dei vetri di spin, è un problema molto difficile e al momento attuale ci sono solo alcuni risultati parziali nell'ambito dell'approssimazione di campo medio. In generale, possiamo distinguere tre regioni temporali: (a) il sistema è stato portato da molto tempo nelle condizioni in cui sono effettuate le misure e ha quindi raggiunto l'equilibrio termico. In questa situazione viene studiata la dinamica veloce che corrisponde al decadimento delle correlazioni a tempi molto più piccoli di quelli necessari per equilibrare il sistema. Una tipica quantità che viene calcolata è la funzione di correlazione:

[15] C(t, t′) ≡ 〈σ_i(t)σ_i(t′)〉

che dipende soltanto dalla differenza dei tempi t−t′ (in quanto siamo all'equilibrio termico). In questo caso sono noti molti risultati, specialmente nell'approssimazione di campo medio: per esempio, sappiamo che nel modello di Sherrington e Kirkpatrick, a basse temperature e per grandi tempi t, la funzione di correlazione è data da

[16] C(t,0) ∼ q_EA + Ct ^−δ(T) + O(t ^−2δ(T))

dove la funzione δ(T) è stata calcolata ed è compresa tra 0,35 e 0,5; (b) come nel caso precedente, consideriamo un sistema all'equilibrio termico. Ora studiamo la dinamica lenta che corrisponde alle transizioni del sistema tra due differenti stati di equilibrio. Questa situazione si può realizzare in pratica soltanto per sistemi piccoli, in quanto un sistema grande ha probabilità pressoché nulla di passare da uno stato di equilibrio a un altro stato di equilibrio; il tempo caratteristico per una tale transizione, infatti, diverge esponenzialmente con le dimensioni del sistema. In questa regione vi sono pochissimi risultati analitici certi, molte simulazioni numeriche e alcuni argomenti semieuristici. Sembra certo che, nel modello di Sherrington e Kirkpatrick, il tempo caratteristico per transizioni fra due stati di equilibrio diverge come exp(CN^λ), con λ non lontano da 1/3; in altri sistemi disordinati diverge ancora più velocemente ed è proporzionale a exp(CN). Questi tempi diventano giganteschi per valori di N non eccessivamente grandi; a tutti gli effetti pratici, a basse temperature, un sistema all'equilibrio rimane congelato in un singolo stato; (c) il sistema era in origine a una temperatura elevata ed è stato raffreddato alla temperatura finale al tempo zero. In presenza di un gran numero di stati, il sistema non raggiunge mai l'equilibrio e si evolve passando per configurazioni di energia sempre minore. La dipendenza dell'energia dal tempo è ben approssimata da

[17] E(t) = E_∞ + Ct^−ν(t)

dove E_∞ è l'energia del sistema all'equilibrio. L'energia tende lentamente verso il suo valore all'equilibrio. In questo caso la funzione di correlazione temporale di due spin ha un comportamento più complesso: C(t,t′) non dipende più solamente dalla differenza dei tempi. Per tempi grandi ‒ nella regione (t/t′)≫1 ‒ in alcuni casi è valida la relazione

[18] formula.

fig. 7

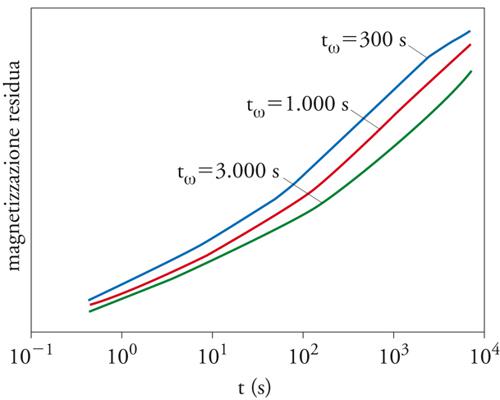
Si può scrivere una corrispondente equazione per le funzioni di risposta. Queste due equazioni implicano che i risultati della misurazione di certe quantità (per es., della suscettività) dipendono fortemente dalla storia precedente del campione. Spesso si osserva un fenomeno molto interessante detto invecchiamento, in base al quale vi è una dipendenza dal tempo che è trascorso dal momento in cui il sistema è stato portato alla temperatura a cui si effettuano le misurazioni. In un esperimento tipico, il sistema è raffreddato al tempo zero in assenza del campo magnetico e dopo un tempo t_ω viene applicato un campo magnetico h molto piccolo. La magnetizzazione osservata dipende dal rapporto t/t_ω (fig. 7). L'invecchiamento è stato osservato sperimentalmente sia nei vetri di spin sia in altri sistemi disordinati (per es., il vetro e la gomma), e dal punto di vista teorico è studiato nell'ambito dell'approssimazione di campo medio, nel quale sono stati ottenuti promettenti risultati analitici. Questo particolare problema dinamico è di grande interesse, in quanto le previsioni teoriche possono facilmente essere confrontate con i da-ti sperimentali e l'invecchiamento è uno fra i problemi su cui è attualmente concentrata l'attenzione degli studiosi dei sistemi disordinati.

Bibliografia

Anderson 1983: Anderson, Philip W., Suggested model for prebiotic evolution: the use of chaos, "Proceedings of the National Academy of Sciences", 80, 1983, pp. 3386-3390.

Balian 1979: La matière mal condensée - Ill-condensed matter, édité par Roger Balian, Roger Maynard, Gérard Toulouse, Amsterdam-Oxford-New York, North-Holland, 1979.

Bangone 1991: Bangone, Gianfranco e altri, Gli ordini del caos, Roma, Manifestolibri, 1991.

Bouchaud 1992: Bouchaud, Jean-Philippe, Weak ergodicity breaking and aging in disordered systems, "Journal de physique", 2, 1992, pp. 1705-1713.

Carnevali, Patarnello 1987: Carnevali, Paolo - Patarnello, Stefano, Boolean networks which learn to compute, "Europhysics letters", 4, 1987, pp. 1199-1204.

Denker 1987: Denker, John e altri, Large automatic learning, rule extraction, and generalization, "Complex systems", 1, 1987, pp. 877-922.

Edwards, Anderson 1975: Edwards, Sam F. - Anderson, Philip W., Theory of spin glasses, "Journal of physics: condensed matter", 5, 1975, pp. 965-974.

Garey, Johnson 1979: Garey, Michael R. - Johnson, David S., Computers and intractability: a guide to the theory of NP-completeness, San Francisco, Freeman, 1979.

Kauffman 1993: Kauffman, Stuart A., The origins of order: self-organization and selection in evolution, New York-Oxford, Oxford University Press, 1993.

Livi 1986: Livi, Roberto e altri, Il computer: da abaco veloce a strumento concettuale, "Il ponte", 42, 1986, 4-5, pp. 41-55.

Livi 1988: Chaos and complexity, Workshop, Torino 1987, edited by Roberto Livi e altri, Singapore, World Scientific, 1988.

Mézard 1987: Mézard, Marc - Parisi, Giorgio - Virasoro, Miguel Ángel, Spin glass theory and beyond, Singapore, World Scientific, 1987.

Parisi 1992: Parisi, Giorgio, Field theory, disorder and simulations, Singapore-London, World Scientific, 1992.

Peliti, Vulpiani 1988: Measures of complexity: proceedings of the conference held in Rome, september 30-october 2, 1987, edited by Luca Peliti, Angelo Vulpiani, Berlin-New York, Springer, 1988.

Rammal 1986: Rammal, Rammal - Toulouse, Gérard - Virasoro, Miguel Ángel, Ultrametricity for physics, "Reviews of modern physics", 58, 1986, pp. 765-795.

Seung 1982: Seung, H. Sebastian - Sompolinsky, Haim - Tishby, Naftali, Statistical mechanics of learning from examples, "Physical review A", 33, 1991, pp. 1978-1982.

Sherrington, Kirkpatrick 1975: Sherrington, David - Kirkpatrick, Scott, Solvable model of a spin-glass, "Physical review letters", 35, 1975, pp. 1792-1796.

Thom 1972: Thom, René, Stabilité structurelle et morphogénèse; essai d'une théorie générale des modèles, Reading (Mass.), Benjamin, 1972 (trad. it.: Stabilità strutturale e morfogenesi. Saggio di una teoria generale dei modelli, Torino, Einaudi, 1980).