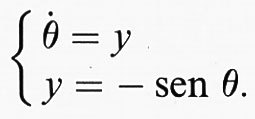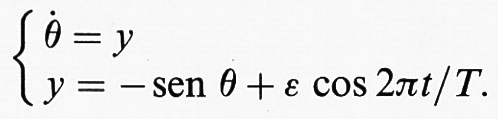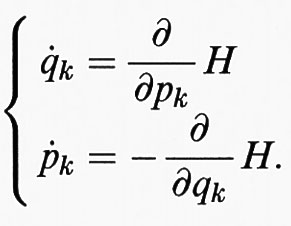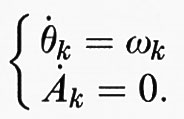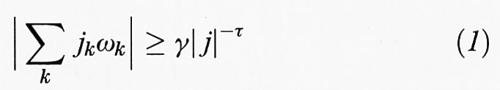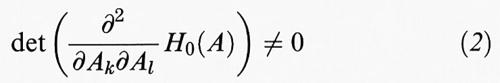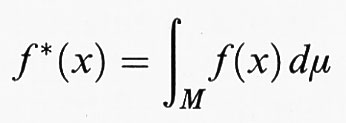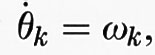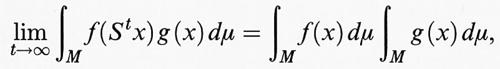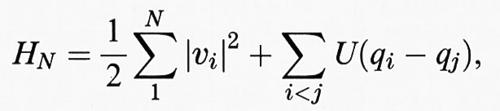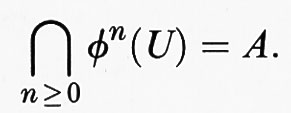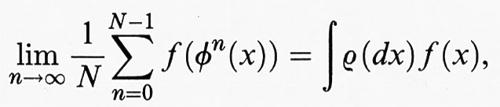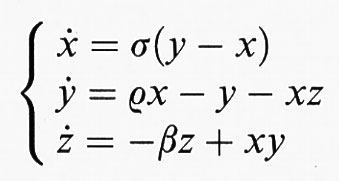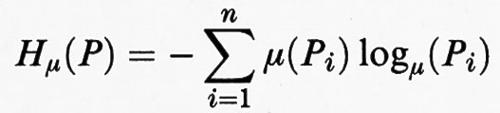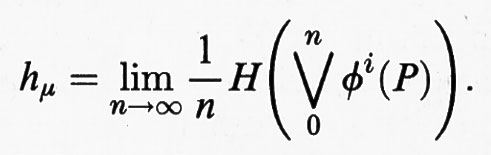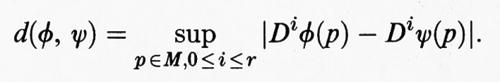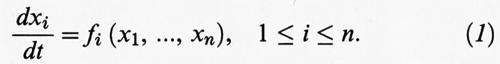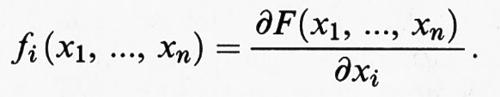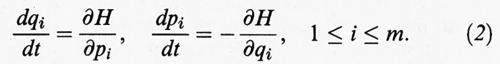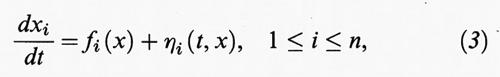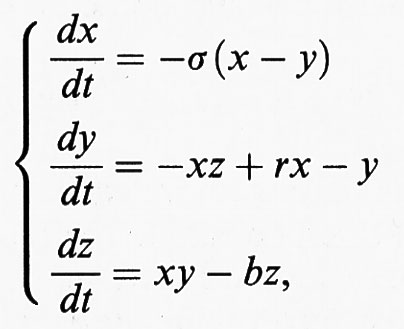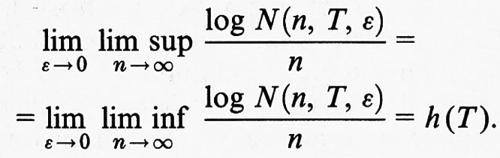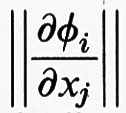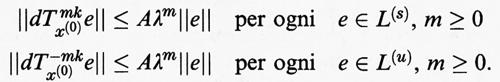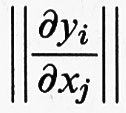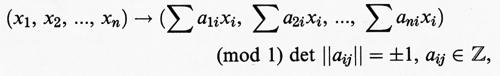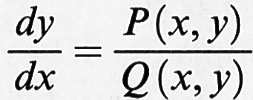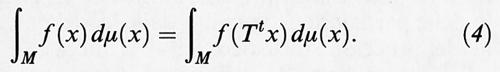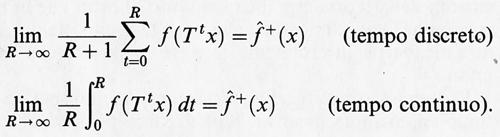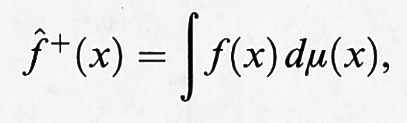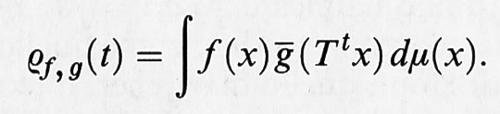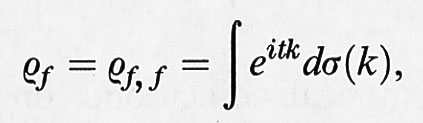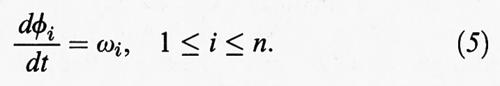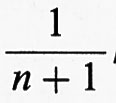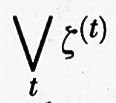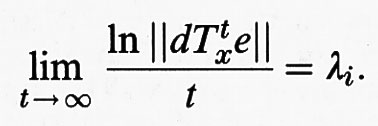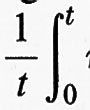Sistemi dinamici

Sistemi dinamici

Origini e sviluppo, di Giovanni Jona-Lasinio

Risultati recenti, di Ya. G. Sinai

Origini e sviluppo di Giovanni Jona-Lasinio

SOMMARIO: 1. Introduzione.  2. Teoria qualitativa dei sistemi non lineari: l'emergere del comportamento caotico.  3. I moti caotici nel sistema solare.  4. La teoria KAM.  5. Teoria statistica dei sistemi dinamici: a) sistemi conservativi; b) sistemi dissipativi; c) entropia e complessità.  6. Stabilità strutturale. □ Bibliografia.

1. Introduzione

Lo studio dei sistemi dinamici consiste nell'analisi delle proprietà delle soluzioni di classi di equazioni differenziali ordinarie o alle derivate parziali, oppure di equazioni alle differenze finite, che descrivono l'evoluzione di sistemi fisici, chimici, biologici, ecc. Si tratta di un settore della matematica pura e applicata che si è sviluppato intensamente a partire dagli anni sessanta. In questo articolo cercheremo di illustrare alcune delle motivazioni, punti di vista e metodi che lo caratterizzano.

Abbiamo parlato di classi di equazioni. Infatti, la teoria dei sistemi dinamici, nei suoi aspetti generali, tende a una classificazione dei sistemi stessi; dunque, come primo passo, vogliamo accennare ad alcuni criteri che la ispirano. Nello studio teorico di qualsiasi sistema fisico reale è inevitabile un processo di maggiore o minore idealizzazione del sistema stesso. Dobbiamo decidere quali sono gli aspetti fondamentali che ci interessano e ignorare tutti quei particolari che ci sembrano non essenziali alla descrizione del fenomeno in studio. Occorre, diceva Galileo, ‟difalcare gli impedimenti". Poiché in una operazione del genere è insita una grande arbitrarietà, il nostro procedimento conoscitivo avrà un senso solo se la nostra descrizione rimarrà sostanzialmente invariata includendo qualcuno degli effetti inizialmente trascurati: in altre parole, la nostra descrizione del sistema dovrà possedere delle buone ‛proprietà di stabilità'. Per essere concreti, consideriamo il moto libero di un pendolo nell'aria, dapprima in un breve intervallo di tempo e successivamente per un tempo molto lungo (rispetto al periodo di oscillazione). Nel primo caso non commettiamo un sensibile errore sia includendo, sia tralasciando la forza di attrito e le proprietà qualitative del moto saranno quelle di un sistema conservativo. Nel secondo caso la dissipazione di energia fa sì che le proprietà del moto risultino completamente diverse se includiamo l'attrito: il moto, anziché persistere, dopo un certo tempo termina. Questo esempio del tutto elementare ci suggerisce una prima possibilità di classificazione dei moti, e quindi dei sistemi dinamici, in conservativi e dissipativi. La nostra scelta della idealizzazione da applicare dovrà innanzi tutto tener conto di questa importantissima distinzione; meno importante sarà invece includere o trascurare degli effetti che non cambino la categoria scelta per il sistema. Ovviamente, la classificazione può procedere per raffinamenti successivi all'interno di ciascuna categoria, dando luogo a sottoclassi di sistemi con proprietà simili che potremo chiamare ‛classi di stabilità'. Il tentativo di arrivare a una classificazione completa dei moti ha costituito la motivazione principale nello sviluppo della cosiddetta ‛teoria qualitativa o geometrica dei sistemi dinamici'.

Tuttavia, nella considerazione dei sistemi dinamici si può adottare un altro punto di vista, che è particolarmente interessante quando si segue il moto per un tempo molto lungo, per cui alcune sue caratteristiche sembrano stabilizzarsi, cioè quando si è in presenza di ‛stati stazionari'. Anche in questo caso ricorriamo a un esempio classico. Consideriamo il sistema costituito dalle molecole di un gas in un recipiente con pareti elastiche. A un certo istante il gas viene fatto espandere in un volume più grande e, dopo qualche tempo, raggiunge uno stato in cui le molecole appaiono comportarsi in modo omogeneo, sia rispetto allo spazio che al trascorrere del tempo. Quando parliamo di comportamento delle molecole non ci riferiamo a una sola di esse, bensì al comportamento medio di gruppi sufficientemente numerosi. Più precisamente, per ‛omogeneità' o ‛stazionarietà' rispetto al tempo intendiamo che le nostre osservazioni - che rappresentano sempre delle medie su intervalli di tempo abbastanza lunghi se confrontati con quelli microscopici e su regioni spaziali abbastanza grandi rispetto alle dimensioni molecolari - non variano sensibilmente se effettuate a tempi diversi e in regioni diverse dello spazio. In altri termini, certe proprietà statistiche del moto si stabilizzano. Nasce quindi l'idea di una possibile classificazione dei moti rispetto alle loro proprietà statistiche.

Lo sforzo di classificazione delle proprietà statistiche dei moti ha dato luogo a quella che viene chiamata ‛teoria ergodica' dei sistemi dinamici. Essa è nata nell'ambito dei sistemi conservativi ed è stata successivamente applicata allo studio dei sistemi dissipativi.

I due filoni che abbiamo menzionato hanno avuto origini storiche diverse e si sono poi intrecciati in molti modi, dando luogo a quella che attualmente viene chiamata ‛teoria del caos deterministico'. È interessante richiamare brevemente alcune tappe di questa evoluzione, a partire dall'idea di stabilità della descrizione accennata sopra. Se una equazione differenziale con cui si descrive un fenomeno fisico è nota solo approssimativamente, essa è utile solo se l'aspetto geometrico delle traiettorie resta qualitativamente lo stesso per piccole variazioni dell'equazione: questa proprietà verrà chiamata in epoca moderna ‛stabilità strutturale'. Dal punto di vista matematico l'idea di stabilità strutturale nasce dal concetto di ‛tipicità' o ‛genericità' di largo uso in matematica, in particolare in topologia. La prima formulazione rigorosa di questa idea fu presentata nel 1937 in un noto lavoro di A. A. Andronov e L. S. Pontryagin, l'uno ingegnere e l'altro matematico, e rifletteva un'esigenza sentita in modo acuto nelle applicazioni tecniche della fisica. Tuttavia, alcune idee fondamentali della teoria qualitativa delle equazioni differenziali sono emerse nell'Ottocento relativamente alla meccanica celeste, dove non si poneva alcun problema di stabilità della descrizione, in quanto le equazioni del moto erano quelle della dinamica newtoniana con interazioni gravitazionali, la cui validità nessuno avrebbe osato mettere in dubbio. I metodi qualitativi vennero sviluppati da H. Poincaré con la scoperta delle cosiddette ‛orbite omocline' nel problema ristretto dei tre corpi. Le orbite omocline sono traiettorie che tendono allo stesso punto quando il tempo tende all'infinito passato e all'infinito futuro. Sotto condizioni molto generali che descriveremo in seguito, l'evoluzione di un sistema nei pressi di un'orbita omoclina è estremamente complessa (si tratta di traiettorie che verranno poi chiamate caotiche) e a questa complessità è associata una perdita di validità dei metodi perturbativi.

Le ricerche di Poincaré vennero sviluppate negli anni trenta da G. D. Birkhoff, il quale mostrò l'esistenza di insiemi molto complicati di orbite periodiche di periodo molto lungo nelle vicinanze di un'orbita omoclina. Si trattava di ricerche di carattere generale e quindi piuttosto astratte. Nuove idee vennero anche dallo studio di equazioni particolari: per costruire modelli del funzionamento delle valvole termoioniche, B. van der Pol introdusse nel 1920 una classe di equazioni, che oggi portano il suo nome, che descrivono oscillatori non lineari con o senza termine forzante. Negli anni quaranta, M. L. Cartwright, J. E. Littlewood e N. Levinson scoprirono che questa classe di equazioni possedeva soluzioni più complicate di qualsiasi soluzione di equazione differenziale nota fino a quel momento. Le ragioni di questa complessità furono chiarite da S. Smale negli anni sessanta, circa settant'anni dopo i lavori di Poincaré.

Dal canto suo, la teoria ergodica, che cerca di analizzare i sistemi dinamici rispetto alle loro proprietà statistiche, è stata identificata dai fisici per lungo tempo con l'analisi della tendenza dei corpi macroscopici (considerati come sistemi meccanici aventi un grandissimo numero di gradi di libertà) a evolvere verso uno stato stazionario di equilibrio. A questo problema è legato in particolare il nome di L. Boltzmann, che introdusse anche il termine ‛ergodico'. Questa teoria si era tuttavia sviluppata inizialmente nell'ambito dei sistemi con pochi gradi di libertà. Per comprenderne le ragioni bisogna tornare a Poincaré e alle sue scoperte in meccanica celeste: infatti, i metodi qualitativi di analisi delle traiettorie da lui sviluppati e applicati al problema dei tre corpi avevano mostrato la possibilità di evoluzioni molto complesse (caotiche) in sistemi con pochi gradi di libertà, e vi è un legame stretto tra le proprietà statistiche di un sistema dinamico e il fatto che le sue traiettorie siano caotiche. I fondamenti della teoria ergodica furono elaborati da Birkhoff, A. Ya. Khinchin e J. von Neumann negli anni trenta; le loro ricerche non affrontarono però lo studio delle proprietà statistiche di sistemi meccanici particolari. Il primo risultato concreto di grande portata è dovuto a Ya. G. Sinai, che negli anni sessanta mostrò le proprietà statistiche di un biliardo con ostacoli (v. sistemi dinamici: Risultati recenti, vol. XI), la cui dimostrazione completa, pubblicata nel 1970, rappresenta un lavoro monumentale. Da allora il progresso è stato molto lento e a tutt'oggi non esiste una trattazione completa delle proprietà statistiche dei sistemi di particelle interagenti che sono oggetto di studio della termodinamica.

Nello stesso periodo, nel 1963, veniva pubblicato un lavoro del meteorologo E. Lorenz, nel quale veniva mostrato numericamente il comportamento caotico di un sistema dinamico a tre gradi di libertà. Si trattava di un sistema ottenuto, attraverso un processo di riduzione, da un'equazione idrodinamica largamente usata nelle previsioni meteorologiche e il risultato di Lorenz indicava chiaramente le ragioni dell'impossibilità di predizioni a lungo termine. Con questo lavoro il caos deterministico oltrepassava la cerchia degli specialisti ed entrava nella cultura scientifica generale. Verso la metà degli anni cinquanta, infine, nasceva un nuovo capitolo della teoria dei sistemi dinamici, la cosiddetta ‛teoria KAM', dalle iniziali dei suoi fondatori, A. N. Kolmogorov, V. I. Arnold e J. Moser. Questa teoria ha costituito una svolta concettuale: infatti, tra le idee prevalenti tra i fisici vi era quella che per ogni sistema valesse l'alternativa fra moti regolari (periodici o quasi periodici) e moti ergodici con forti proprietà statistiche. La teoria KAM ha mostrato invece che esistono situazioni intermedie in cui sono presenti gli uni e gli altri in proporzioni arbitrarie.

2. Teoria qualitativa dei sistemi non lineari: l'emergere del comportamento caotico

Il pendolo. - Introduciamo alcune idee partendo dal semplice esempio del pendolo, che rappresenta un caso paradigmatico. Esso è descritto dall'equazione del secondo ordine θ¨ = -sen θ, dove θ misura la deviazione angolare del pendolo dalla verticale. Si sono scelte unità in cui tutte le costanti fisiche sono uguali a 1. Possiamo riscrivere questa equazione come sistema del primo ordine

Nell'analisi delle equazioni differenziali è opportuno passare a una descrizione ridotta in cui le soluzioni vengono considerate a istanti di tempo discreti, ad esempio multipli di un dato tempo T. Definiamo allora la trasformazione ϕ (θ, y) = (θè, å) quando la soluzione del nostro sistema è tale che (θ (0), y (0)) = (θ, y) e (θ (T), y (T)) = (θè , å). La trasformazione ϕ possiede due punti fissi in corrispondenza alle posizioni di equilibrio del pendolo (θ = 0, y = 0) e (θ = π, y = 0). La prima è una posizione di equilibrio stabile, mentre la seconda è instabile. Concentriamoci sulla posizione instabile e definiamo le corrispondenti varietà stabile e instabile. In generale, dato un punto fisso p di una trasformazione, a esso possono essere associate una ‛varietà stabile' W^s (p) = {x : ϕⁱ (x) → p, i → + ∞} e una ‛varietà instabile' W^u (p) = {x : ϕⁱ (x) → p, i → - ∞}, dove i indica il numero di iterazioni della trasformazione. Nel nostro caso x rappresenta la coppia (θ, y) e la conservazione dell'energia ci dice che entrambe le varietà sono descritte dall'equazione - cos θ + 1/2 y² = 1 e sono perciò coincidenti. La traiettoria che inizia e termina nella posizione di equilibrio instabile è un'orbita omoclina. Se ora perturbiamo leggermente l'equazione del pendolo in modo tale da rimuovere la degenerazione tra la varietà stabile e quella instabile, queste si incontreranno almeno in un punto q, detto ‛punto omoclino'. Iterando allora la trasformazione del punto omoclino ci rendiamo conto che, per la loro stessa definizione, le due varietà dovranno intersecarsi infinite volte (v. fig. 1). È questo un meccanismo fondamentale di generazione del comportamento caotico. Infatti, le infinite intersezioni costringono le varietà stabile e instabile ad avere una struttura geometrica molto complessa che si trasmette alle orbite vicine. La conseguenza è che due punti vicini tra loro nei pressi di un punto omoclino tenderanno ad avere storie molto diverse e a perdere memoria uno dell'altro iterando la trasformazione. Questo fenomeno, nella letteratura moderna, viene chiamato ‛dipendenza sensibile dalle condizioni iniziali', e lo illustreremo in dettaglio più avanti. La natura caotica del moto può essere rivelata registrando ad esempio i tempi di passaggio del pendolo nella posizione più bassa: si può mostrare che essi formano una sequenza di numeri non distinguibile da una sequenza casuale (preciseremo questo punto nella successiva discussione relativa al problema dei tre corpi). Per ottenere un punto omoclino basta aggiungere alle equazioni del pendolo una piccola perturbazione periodica, ad esempio modificando le equazioni come segue:

La trasformazione discreta naturale da considerare è quella che corrisponde a un intervallo di tempo uguale al periodo della perturbazione esterna. Naturalmente, non tutte le condizioni iniziali danno luogo a moti caotici, e l'analisi delle diverse regioni dello spazio delle fasi rispetto ai tipi di moto possibili è molto complessa.

Il problema ristretto dei tre corpi. - Prima di descrivere un po' più in dettaglio il meccanismo che genera il caos, citiamo un altro esempio che, come abbiamo accennato nel cap. 1, ha avuto un ruolo storico di grande importanza: il problema ristretto dei tre corpi. Si considerino due corpi puntiformi di massa uguale soggetti all'attrazione newtoniana. Essi descriveranno orbite ellittiche in un piano e il loro baricentro sarà in quiete (v. fig. 2). Si consideri poi una terza massa, trascurabile rispetto alle prime due, che si muove perpendicolarmente al piano precedente lungo una retta che passa per il baricentro delle prime due. Il problema consiste nello studiare il moto del terzo corpo, in particolare gli istanti di attraversamento del piano. Se indichiamo con z la quota di questo corpo, la legge di gravitazione di Newton fornisce l'equazione ü = - z/(z² + r² (t))^3/2, in cui r (t) è una funzione periodica che rappresenta la distanza di una delle due masse grandi dal baricentro e può scriversi nella forma r (t) = 1/2 (1 - ε cos t) + O (ε²), dove ε è l'eccentricità, che si suppone piccola. Si dimostra che esistono orbite che compiono infinite oscillazioni e che i tempi di attraversamento del piano z = 0 costituiscono una successione non distinguibile da una successione casuale. Più precisamente, il risultato è il seguente: si consideri una soluzione dell'equazione precedente che attraversi infinite volte il piano z = 0 negli istanti t_k con k = 0, ± 1, ± 2, ..., ordinati secondo valori crescenti. Si introducano gli interi s_k = [(t_k⁺¹ - t_k)/2 π] che misurano il numero di rivoluzioni complete delle masse grandi tra uno zero e l'altro di z (t), [a] rappresenta la parte intera di a. Allora per eccentricità ε sufficientemente piccole esiste un numero m (ε) tale che qualsiasi successione di interi s_k ≥ m corrisponde a una soluzione dell'equazione differenziale. È chiaro l'interesse di simili risultati per l'astronomia. Lo studio dei moti caotici del sistema solare ha avuto notevolissimi sviluppi negli ultimi anni, con risultati sorprendenti (v. cap. 3).

Il modello di Smale del ferro di cavallo. - Il meccanismo geometrico fondamentale che produce un comportamento caotico in presenza di intersezioni omocline è stato chiarito da Smale negli anni sessanta attraverso la costruzione di un modello a cui è possibile ricondursi sotto condizioni molto generali. Tale modello viene chiamato il ‛ferro di cavallo' e lo illustreremo brevemente. Si consideri nel piano un quadrato Q che assoggettiamo a una trasformazione ϕ = f₂ 0 f₁ ottenuta dall'applicazione in successione di due operazioni più semplici f₁ e f₂: la prima operazione consiste nel contrarre linearmente il quadrato nella direzione orizzontale e dilatarlo in quella verticale; la seconda operazione f₂ consiste nel ripiegare a ferro di cavallo il rettangolo ottenuto dalla prima operazione come indicato nella fig. 3A. Indichiamo con V₁ e V₂ le intersezioni di ϕ (Q) con Q. Le iterazioni successive si costruiscono nel modo seguente: l'iterazione al passo n + 1 agisce sull'intersezione con il quadrato di partenza dell'insieme ottenuto al passo n. Smale considera allora l'insieme Λ dei punti che non escono mai da Q quando si applica ϕ. Per definizione Λ = ⋂_^∞_∞ ϕⁿ (Q). È facile rendersi conto che ⋂^N_-N ϕⁿ (Q) è costituito dalle intersezioni di strisce verticali e orizzontali, queste ultime corrispondenti ai valori negativi di n, di larghezza decrescente (v. fig. 3B): si dimostra che il limite per N che tende all'infinito è un insieme di Cantor.

A ogni punto p di Λ si può ora associare una sequenza infinita di simboli {s_k}, dove s_k può assumere i valori di 1 o 2, in base alla regola ϕ^k (p) ∈ V_sk. A ogni punto si fa quindi corrispondere la storia delle sue visite nelle strisce verticali V₁ e V₂ sotto l'azione della trasformazione. Si dimostra che questa corrispondenza è biunivoca e bicontinua, cioè che si tratta di un omeomorfismo. Si può ora comprendere facilmente il comportamento caotico della dinamica sull'insieme Λ. Data una sequenza di lunghezza finita {s_k} con ∣k∣ ≤ N, essa corrisponde a un sottoinsieme infinito (non numerabile) di punti di Λ, cioè tutti i punti che hanno questa sequenza come segmento iniziale; le storie successive di tali punti, tuttavia, sono indipendenti, poiché per k maggiore di N i simboli corrispondenti possono essere scelti arbitrariamente.

Torniamo allora ai punti omoclini. Con riferimento alla fig. 1 si immagini di costruire un piccolo parallelogramma R che contenga il punto q. Ad esempio, si possono prendere per lati due segmenti giacenti l'uno sulla varietà instabile W^u (p) e l'altro su quella stabile W^s (p) e intersecantisi in q. Gli altri due lati saranno segmenti paralleli ai precedenti e uscenti dalle estremità opposte a q. Si può allora dimostrare che una opportuna potenza ϕ^l della trasformazione che definisce la dinamica possiede un insieme invariante Λ ⊂ R su cui le traiettorie sono caotiche in modo del tutto analogo a quelle del ferro di cavallo di Smale. Questo risultato è noto con il nome di teorema di Birkhoff-Smale.

3. I moti caotici nel sistema solare

Il caos è presente un po' ovunque nel sistema solare. Esso è presente nel moto dei corpi minori come gli asteroidi, le comete e i piccoli satelliti, ad esempio il satellite di Saturno Iperione. Ma anche i pianeti maggiori hanno probabilmente avuto periodi di moto caotico nella loro storia, specialmente per quanto riguarda l'evoluzione della loro ‛obliquità', vale a dire l'inclinazione del piano equatoriale del pianeta rispetto al piano dell'orbita. È stato dimostrato che l'obliquità della Terra è attualmente stabile a causa della presenza della Luna, a cui dobbiamo quindi la possibilità stessa della vita. L'inclinazione di Marte subisce invece grandi variazioni caotiche tra 0° e 60°. Su periodi dell'ordine del miliardo di anni, anche le orbite dei pianeti presentano importanti variazioni caotiche che potrebbero portare a una fuga di Mercurio dal sistema solare o a una sua collisione con Venere.

L'interesse che riveste lo studio dei moti caotici nella storia del sistema solare è legato alla possibilità o meno di ottenere informazioni sulla formazione del sistema stesso a partire dai dati alla situazione attuale. Ad esempio, se le obliquità dei pianeti osservate potessero identificarsi con quelle primordiali avremmo un vincolo nell'interpretazione del processo di formazione. Purtroppo questo non è il caso. I grandi progressi recenti nella simulazione della dinamica planetaria permettono di ricostruire in modo attendibile la storia del sistema per molti milioni di anni, e mostrano che moti caotici sono intervenuti nell'evoluzione dell'obliquità di tutti i pianeti per effetto delle loro interazioni reciproche. È interessante notare che lo studio di questo problema si riduce all'analisi di perturbazioni quasi periodiche di un oscillatore, il cui prototipo è l'esempio del pendolo perturbato da noi considerato nel capitolo precedente.

4. La teoria KAM

Ci si può chiedere a questo punto come siano possibili i moti regolari che appaiono dominanti nel sistema solare e a cui dobbiamo una situazione sufficientemente tranquilla da garantire la nostra esistenza. Una risposta qualitativa a questa domanda viene dalla teoria di Kolmogorov-Arnold-Moser, o teoria KAM, che trae la sua origine dal seguente problema di stabilità. Consideriamo le equazioni di un sistema meccanico in forma hamiltoniana. Esso è descritto da coordinate e momenti (q₁, ..., q_n, p₁, ..., p_n) che soddisfano le equazioni

Supponiamo che esista una trasformazione canonica che permetta di passare a nuove variabili A_k, θ_k tali che le equazioni del moto prendano la forma

Le A_k sono quindi costanti del moto, mentre le θ_k effettuano un moto periodico o quasi periodico se le frequenze ω_k sono tra loro razionalmente indipendenti. In tale situazione si dice che il sistema è ‛integrabile'. Ci chiediamo cosa accade se perturbiamo debolmente un sistema integrabile. Sia H₀ (A₁, ..., A_n) la funzione hamiltoniana non perturbata e supponiamo che il sistema perturbato sia descritto dalla hamiltoniana

dove μ è un parametro piccolo e H è una funzione analitica reale di 2 n + 1 variabili; H₁ è periodica nelle θ_k. Ci chiediamo in particolare cosa accade dei moti quasi periodici descritti da H₀ quando si accende la perturbazione. Consideriamo quelle frequenze ω_k =

H₀ (A) che, oltre a essere razionalmente indipendenti, soddisfano la condizione

per tutti gli interi j_k tali che ∣j∣ = Σ_k ∣j_k∣ ≥ 1, con γ e τ costanti positive. Il teorema KAM afferma che sotto la condizione aggiuntiva

per piccoli valori di ∣μ∣ si possono trovare nuove coordinate θ′ tali che θk′ = ω_k. È importante sottolineare che le frequenze ω_k vengono mantenute fisse quando si accende la perturbazione. Ciò è reso possibile dalla condizione supplementare (2).

Per molto tempo si è ritenuto che le perturbazioni dei sistemi integrabili distruggessero tutti i moti quasi periodici dando luogo a un comportamento caotico. Il teorema KAM, nella forma in cui l'abbiamo enunciato, può dare l'impressione che sia vero esattamente l'opposto, cioè che essenzialmente tutti i moti quasi periodici vengano conservati, poiché il complemento dell'insieme delle frequenze che soddisfano alla relazione (1) per qualche valore di γ e τ ha misura nulla. In realtà, la condizione che il parametro μ sia sufficientemente piccolo dipende dal valore di γ e ciò implica che non tutti i moti quasi periodici sopravvivono alla perturbazione. Il teorema KAM stabilisce quindi che ‛una parte' dei moti quasi periodici viene preservata dalla perturbazione. Questa affermazione significa che le condizioni iniziali nello spazio delle fasi che danno luogo a moti quasi periodici costituiscono un insieme di volume positivo. Ciò empiricamente fu scoperto in un celebre esperimento numerico di Fermi, Pasta e Ulam, di poco precedente il primo lavoro di Kolmogorov sull'argomento, consistente nello studio dell'equipartizione dell'energia tra i gradi di libertà di una catena di oscillatori non lineari interagenti debolmente. Il sorprendente risultato dell'esperimento fu che non si osservava alcuna equipartizione.

5. Teoria statistica dei sistemi dinamici

a) Sistemi conservativi.

In una visione gerarchica e newtoniana del mondo naturale, i sistemi considerati sono conservativi. Infatti, dalla scala planetaria a quella atomica e subatomica le forze che agiscono tra elementi di materia sono conservative, e la grande maggioranza dei fisici ritiene che se esiste una teoria ultima del mondo - una teoria del ‛tutto', come si usa dire attualmente - questa debba essere basata su un modello conservativo. È quindi naturale esaminare i sistemi conservativi per primi, anche perché a essi si riferisce il problema della tendenza all'equilibrio dei sistemi termodinamici posto da Boltzmann nel secolo scorso. Occorre dire subito che questo problema a tutt'oggi non ha avuto una soluzione soddisfacente: la sua formulazione matematica è tutt'altro che ovvia e alla fine di questo paragrafo discuteremo alcune impostazioni possibili. Molte difficoltà sono legate alla necessità di considerare un numero di gradi di libertà che tende all'infinito.

I sistemi conservativi classici posseggono misure invarianti naturali. L'esistenza di misure invarianti è un'ipotesi fondamentale della teoria ergodica. Cominciamo con l'introdurre alcuni concetti della teoria ergodica che sono indipendenti dal numero di gradi di libertà del sistema. Sia M un insieme sulla cui natura non facciamo ipotesi particolari e supponiamo che sui sottoinsiemi di M sia assegnata una misura di probabilità μ. Per fissare le idee, M può essere l'insieme delle posizioni e delle velocità accessibili a un sistema dinamico, cioè lo spazio delle fasi (di solito una varietà differenziabile), ma può anche essere costituito da elementi discreti. Definiamo la ‛dinamica' come un gruppo di trasformazioni di M che dipendono da un parametro t e conservano la misura. Se indichiamo con S^t tali trasformazioni, avremo μ (A) = μ (S^t A) = μ (S^-t A), dove A ⊂ M. La terna (M, S^t, μ) viene chiamata un ‛sistema dinamico astratto' e costituisce l'ambiente naturale per lo sviluppo della teoria ergodica. Il primo teorema ergodico, dimostrato da von Neumann nel 1929, affermava che al tendere di T all'infinito si ha

dove f è una funzione a quadrato integrabile definita su M. La funzione f^* ha le seguenti proprietà: a) è invariante, vale a dire, f^* (S^t x) = f^* (x); b) ∫_M fdμ = ∫_M f^*dμ. La convergenza è quella della media quadratica. Il teorema fu poco dopo raffinato da Birkhoff e Khinchin che, indipendentemente, mostrarono la convergenza ‛per quasi tutti' i punti iniziali x (questa locuzione significa per tutti i punti x eccetto un insieme di misura o probabilità zero).

Il contenuto di questi teoremi implica che la media temporale, per la classe delle funzioni considerate, tende a stabilizzarsi al crescere del tempo e dipende solo dall'orbita passante per x. Un risultato così generale è un buon punto di partenza, poiché la misura di una qualunque grandezza fisica relativa a un sistema termodinamico richiede tempi lunghi rispetto a quelli della dinamica microscopica (tempi di collisione tra le molecole) e deve quindi intendersi come una media temporale della grandezza in questione. Tuttavia, la nostra intuizione vorrebbe che non ci fosse neppure la dipendenza dall'orbita considerata. Infatti, quando studiamo, per esempio, un gas, noi fissiamo solo alcune grandezze macroscopiche come energia totale, pressione o temperatura, e non abbiamo alcuna idea di quale sia lo stato dinamico delle molecole. Una tale proprietà di indipendenza delle medie temporali dall'orbita considerata in generale non è vera. Chiameremo ‛ergodici' solo quei sistemi per cui le medie temporali sono delle costanti. In tal caso

per quasi tutti i punti x, cioè per tutti gli x meno un insieme di μ-misura 0. Sistemi ergodici sono, ad esempio, i sistemi integrabili della meccanica classica quando le frequenze sono razionalmente indipendenti: si tratta, cioè, dei sistemi di equazioni lineari

dove k = 1, 2, ..., n, θ_k sono variabili angolari su di un toro a n dimensioni e ω_k sono numeri reali razionalmente indipendenti. Quest'ultima ipotesi fa sì che le orbite del sistema siano dense sul toro. La misura invariante è data dall'elemento di volume. Si comprende quindi facilmente come la densità delle orbite permetta l'uguaglianza delle medie temporali con quelle spaziali. L'importanza dell'ergodicità sta nel fatto che essa permette di sostituire lo studio della dinamica, praticamente impossibile quando il numero dei gradi di libertà è elevato, con il calcolo di medie effettuate con la misura invariante μ, che chiameremo anche ‛misura di equilibrio'. In particolare, una importante conseguenza dell'ergodicità è che, se nel teorema precedente noi scegliamo una funzione f che valga uno su una data regione dello spazio delle fasi e zero altrove, troviamo che la percentuale di tempo spesa dal sistema dentro quella regione è pari alla probabilità di trovare il sistema in quella regione. Questa considerazione ha avuto un ruolo rilevante nel pensiero di Boltzmann.

Tuttavia l'ergodicità non è sufficiente per lo scopo dei fisici: occorre rendersi conto che mentre assicura la sostituibilità delle medie temporali con medie fornite da una distribuzione di probabilità invariante nel tempo, essa non assicura che tale distribuzione venga raggiunta a partire da una diversa distribuzione iniziale. Perché questo avvenga è necessaria una proprietà più forte che è definibile nella forma seguente: il sistema dinamico (M, S^t, μ) è mescolante (mixing) se la dinamica rende i sottoinsiemi di M statisticamente indipendenti. Ciò si può esprimere matematicamente come segue:

dove f e g sono funzioni a quadrato integrabile. Mostriamo allora che se il nostro sistema è mescolante e inizialmente descritto da una distribuzione di probabilità μ₀, questa evolverà tendendo asintoticamente alla distribuzione di equilibrio μ. L'evoluzione è definita dall'equazione μ_t (A) = μ₀ (S^-t A), dove A è un sottoinsieme di M; sotto un'ipotesi aggiuntiva che poi commenteremo, μ_t (A) tende a μ (A). L'ipotesi aggiuntiva è che μ₀ (A) = ∫_A p (x) dμ, cioè μ₀ possiede una densità rispetto alla misura di equilibrio μ. Infatti in tal caso

dove χ_A è la funzione indicatrice dell'insieme A. L'argomento è identico se sostituiamo χ_A con qualsiasi funzione a quadrato integrabile. Ne risulta che i valori medi sulla distribuzione iniziale di una grandezza fisica tendono ai valori medi calcolati con la distribuzione di equilibrio e quindi coincidono con le medie temporali.

Cerchiamo di capire meglio il risultato ottenuto. L'ipotesi che μ₀ possieda una densità rispetto alla misura di equilibrio μ esclude il caso in cui il sistema parte da uno stato iniziale determinato x₀. In tal caso infatti la misura iniziale si ridurrebbe a una δ di Dirac. In altre parole, riusciamo a dimostrare che il sistema evolve verso l'equilibrio se il suo stato iniziale è noto solo approssimativamente e ci accontentiamo di una descrizione incompleta, cioè probabilistica. È tuttavia molto interessante il fatto che esistano sistemi a un numero finito di gradi di libertà ergodici e mescolanti. Tra questi ricordiamo il moto geodetico su una superficie a curvatura negativa studiato da J. Hadamard nel 1898. Molti sistemi della meccanica classica possono ridursi a questo caso.

Dobbiamo peraltro sottolineare la differenza tra i sistemi a numero finito di gradi di libertà e i sistemi termodinamici. Nel primo caso, infatti, anche se i valori medi delle grandezze fisiche rappresentate dalle diverse funzioni f tendono ai corrispondenti valori di equilibrio, le grandezze stesse avranno in generale fluttuazioni rispetto ai valori medi, sia durante l'evoluzione che una volta raggiunto l'equilibrio. I sistemi macroscopici, invece, tendono all'equilibrio in modo deterministico. Infatti, l'evoluzione delle grandezze fisiche è spesso retta da equazioni alle derivate parziali come quelle dell'idrodinamica. Questo comportamento deterministico è dovuto al fatto che le variabili macroscopiche rappresentano medie su un grandissimo numero (al limite infinito) di gradi di libertà e quindi sono stabilizzate dalle leggi dei grandi numeri.

La teoria ergodica ha dato finora pochi risultati quando i gradi di libertà del sistema sono infiniti (limite termodinamico). In questo caso interviene un nuovo meccanismo che porta all'ergodicità e al mescolamento e che può essere descritto come la possibilità di trasformare il caos spaziale in caos temporale. A causa dell'estensione infinita del sistema, una configurazione (ad esempio di un gas) spazialmente caotica, se osservata su una regione spaziale finita, apparirà caotica nella sua evoluzione temporale, poiché la dinamica fa passare sotto gli occhi dell'osservatore le configurazioni esistenti in altre regioni. Si tratta evidentemente di un meccanismo che può agire anche in sistemi non interagenti come un gas perfetto. In effetti, ergodicità e mescolamento sono stati rigorosamente dimostrati per il gas perfetto, per il cristallo armonico e per sistemi riconducibili a questi, mentre per modelli di un gas di particelle interagenti sono stati ottenuti risultati analoghi solo introducendo ipotesi ad hoc, come una sorgente di stocasticità esterna al sistema e limitazioni non naturali sulla forma dell'energia cinetica.

Vogliamo descrivere brevemente lo stato attuale dell'arte in relazione al problema della tendenza all'equilibrio. Dalla discussione precedente emerge il fatto che il grande numero di gradi di libertà deve avere un ruolo cruciale, come del resto è avvenuto nella spiegazione delle transizioni di fase da parte della meccanica statistica dell'equilibrio. Indicheremo alcune delle difficoltà matematiche principali. Occorre dimostrare che la dinamica di un gas di molecole interagenti ha un senso anche quando il numero delle molecole cresce indefinitamente e diventa infinito nel limite termodinamico. Non si tratta di un problema banale, poiché particolari configurazioni del gas, come la concentrazione di infinite particelle in una regione finita, possono dar luogo a evoluzioni catastrofiche. Si procede allora nel seguente modo: si parte da una funzione hamiltoniana relativa a N particelle (molecole) del tipo

dove v_i sono le velocità delle particelle e U è un potenziale di interazione tra le coppie di particelle. Poiché per qualunque configurazione iniziale l'evoluzione data dalle corrispondenti equazioni del moto non è ben definita quando N → ∞, si cerca di dimostrare che essa esiste almeno per un insieme di configurazioni iniziali che ha probabilità 1 rispetto a una misura invariante di riferimento. Si ritiene che le misure di riferimento rilevanti siano le misure di equilibrio di Gibbs, ad esempio la misura canonica μ_N = (exp - β H_N)/Z_N, il cui limite per N → ∞ esiste per una vasta scelta di potenziali di interazione. Z_N è il fattore di normalizzazione (funzione di partizione).

Quando questo programma ha successo si dice che ‛esiste la dinamica dell'equilibrio'. Per arrivare a dimostrare che l'evoluzione tende all'equilibrio occorrono proprietà ben più forti. Ad esempio, sarebbe molto soddisfacente mostrare che per una vasta classe di distribuzioni iniziali che non hanno necessariamente una densità rispetto alla distribuzione di equilibrio vale la relazione

dove μ_t designa l'evoluzione temporale della distribuzione iniziale μ₀. La convergenza è quella debole per le misure di probabilità, cioè la convergenza dei momenti delle distribuzioni. Tipicamente le distribuzioni iniziali che hanno una densità diversa rispetto a quella di equilibrio comportano alterazioni di quest'ultima solo in regioni limitate dello spazio delle fasi del sistema, e quindi coinvolgono solo un numero finito di gradi di libertà. Una situazione del tutto ovvia dal punto di vista fisico, come quella di un gas in cui la densità iniziale differisca da quella di equilibrio per una modulazione periodica, non rientra tra queste e risultati del tipo indicato non sono noti per alcun modello deterministico di particelle interagenti. La dimostrazione di proprietà di mescolamento per grandezze fisiche che dipendono da un numero finito di variabili non è sufficiente per stabilire l'equazione (3).

In conclusione, i problemi posti da Boltzmann oltre un secolo fa costituiscono ancora oggi una grande sfida per la teoria dei sistemi dinamici.

b) Sistemi dissipativi.

L'ipotesi dell'esistenza di misure invarianti non è verificata nei sistemi dinamici che descrivono fenomeni dissipativi. I fenomeni dissipativi che ci interessano maggiormente sono quelli in cui il sistema, nella sua evoluzione, dopo una fase transiente raggiunge uno stato stazionario nel quale è mantenuto dall'azione costante di una sorgente di energia: un esempio di grande interesse è rappresentato dagli stati turbolenti di un fluido. Uno sviluppo molto importante della teoria moderna dei sistemi dinamici ha permesso di estendere la teoria ergodica a tali situazioni. Per comprendere come ciò sia possibile è necessario introdurre alcuni concetti nuovi.

Un concetto basilare è quello di attrattore. In termini semplici, un attrattore è un insieme compatto, nello spazio delle variabili che descrivono un sistema, verso cui tendono tutte le traiettorie che iniziano nelle sue vicinanze. Un caso molto elementare si ottiene riprendendo in considerazione l'esempio del pendolo, ma questa volta introducendo una forza di attrito. In tal caso al crescere del tempo tutte le traiettorie tendono verso la posizione di equilibrio θ = 0, y = 0. Un caso più interessante, che si incontra nella teoria degli oscillatori di van der Pol, è il ciclo limite, cioè un'orbita periodica che al crescere del tempo attrae tutte le traiettorie vicine. La teoria moderna dei sistemi dissipativi ha messo in luce l'esistenza e l'importanza nelle applicazioni di attrattori più complessi (attrattori strani) sui quali il moto è caotico.

Per dare una definizione formale di attrattore consideriamo ancora, per fissare le idee, una dinamica con tempo discretizzato. Diremo che un insieme compatto A invariante sotto la trasformazione ϕ, cioè ϕ (A) = A, è un attrattore se esiste un suo intorno U tale che

Un attrattore si dice ‛strano' se contiene un'orbita omoclina con autointersezioni trasversali, cioè punti omoclini. Per le trasformazioni ϕ differenziabili almeno due volte insieme alle loro inverse (diffeomorfismi di classe C^r con r ≥ 2) e che soddisfano delle ipotesi che vengono usualmente indicate con il nome di ‛assioma A', si può dimostrare che: a) ϕⁿ (x) tende verso un attrattore quando n → ∞ per quasi ogni x rispetto alla usuale misura di volume; b) per ogni funzione continua f (x)

ρ è una misura definita sull'attrattore in modo univoco. La proprietà b) è una proprietà ergodica e mostra che una volta che il sistema ha raggiunto l'attrattore si comporta in modo simile ai sistemi conservativi.

I sistemi che soddisfano all'assioma A di Smale sono caratterizzati nel modo seguente: sia M una varietà compatta di classe C^∞, ϕ un diffeomorfismo di classe C^r che agisce su M. Diremo che un sottoinsieme X di M è ‛iperbolico' se l'iperpiano tangente a M in ogni punto x ∈ X può decomporsi nella somma di due sottospazi E^u, E^s sui quali l'azione di D ϕ, differenziale di ϕ nel punto x, è dilatante e contraente, rispettivamente. Ciò significa che gli autovalori della matrice D ϕ (x) sono maggiori di 1 nel sottospazio E^u, e minori di 1 nel sottospazio E^s. Un punto x di M si dice ‛vagante' se esiste un suo intorno U tale che U ⋂ ϕⁿ (U) = 0/ per ogni n positivo. Sia Ω l'insieme dei punti non vaganti; diremo che il sistema dinamico descritto dal diffeomorfismo ϕ verifica l'assioma A se sono soddisfatte le seguenti due ipotesi: 1) l'insieme Ω è iperbolico; 2) i punti periodici di ϕ, cioè i punti x tali che esiste un intero m per cui ϕ^m (x) = x, sono densi in Ω.

Dimostrare rigorosamente che un dato sistema dinamico possiede un attrattore strano non è semplice. Tra i sistemi di interesse fisico che si ritengono rientrare in tale categoria vi è quello di Lorentz menzionato nell'introduzione. Esso è definito dalle tre equazioni seguenti

con σ, ρ, β costanti positive.

Anche nel caso dissipativo sono stati studiati sistemi a infiniti gradi di libertà. Per i sistemi infiniti, conservativi o dissipativi, è stata introdotta una nozione di caos spazio-temporale corrispondente a una proprietà di mescolamento simultanea rispetto alla dinamica e alle traslazioni spaziali. Si consideri ad esempio il reticolo dei punti a coordinate intere in uno spazio a d dimensioni. Data una funzione, in generale vettoriale u (x) definita sul reticolo, l'operatore di traslazione agisce nel modo seguente: T^z u (x) = u (x - z), dove z è un vettore del reticolo. Supponiamo ora che in ciascun punto del reticolo vi sia una copia di un sistema caotico a un numero finito di gradi di libertà. Indichiamo con u (x) la posizione nel proprio spazio delle fasi del sistema che si trova in x. Supponiamo inoltre che ciascun sistema interagisca con i propri vicini che si trovano a una distanza minore di R. La configurazione dell'intero sistema sarà evidentemente specificata dall'assegnazione di una funzione u (x). Sia S^t l'operatore che descrive l'evoluzione dell'intero sistema e consideriamo l'azione simultanea della dinamica e delle traslazioni. Diremo che il sistema presenta caos spazio-temporale se, data una misura μ invariante sotto tale azione, si verifica che

con F e G funzionali limitati di u. È stato dimostrato che i sistemi descritti sopra, sotto opportune ipotesi, presentano caos spazio-temporale. Si tratta di risultati interessanti poiché forniscono un modello ancora qualitativo ma rigoroso di fenomeni spazialmente caotici come i flussi turbolenti. Inoltre, questi sistemi possono dar luogo a situazioni analoghe alle transizioni di fase e per questa via si ritiene possibile spiegare la comparsa di strutture spaziali (strutture coerenti) che si osserva in esperimenti sia reali che numerici di meccanica dei fluidi.

c) Entropia e complessità.

In quest'ultimo paragrafo vogliamo brevemente discutere come si può caratterizzare quantitativamente il comportamento caotico dei sistemi dinamici. Ci riferiamo a sistemi dinamici che posseggono una misura invariante, quindi sistemi conservativi o sistemi dissipativi il cui moto sia ristretto agli attrattori.

Il concetto di entropia è fondamentale. L'entropia di un sistema dinamico, chiamata anche entropia di Kolmogorov-Sinai, si definisce nel modo seguente. Sia P = (P₁, ..., P_n una partizione dell'insieme M su cui è definita la misura μ. Definiamo

entropia della partizione. L'entropia della trasformazione ϕ rispetto alla partizione P è data da

Date n partizioni P_i, la partizione ⋁_iP_i è costituita da tutte le possibili intersezioni della forma π₁ ⋂ π₂ ⋂ .... ⋂ π_n, con π_i ∈ P_i. L'entropia di Kolmogorov-Sinai si ottiene prendendo l'estremo superiore rispetto a tutte le possibili partizioni. Sinai ha mostrato che non è necessario effettuare questa difficile operazione, poiché esistono partizioni dette ‛generanti' che danno direttamente il risultato desiderato.

Un sistema viene considerato fortemente caotico se ha entropia positiva; essa fornisce una misura della diversificazione delle traiettorie sotto l'azione della dinamica. È facile rendersi conto, ad esempio, che se i moti sono periodici il numero di elementi della partizione ⋁0ⁿ ϕⁱ (P) rimane finito al crescere di n e l'entropia in questo caso è 0. L'entropia è una quantità che riguarda il comportamento statistico dell'insieme di tutte le traiettorie.

Un interessante teorema di A. Brudno del 1978 consente di mettere in relazione la caoticità delle singole traiettorie con l'entropia. La caoticità di una singola traiettoria può essere caratterizzata mediante la complessità di Kolmogorov, che è definita nel modo seguente: sia A un calcolatore e p un programma costituito per esempio da una sequenza finita di simboli 0 o 1. Il numero dei simboli è la lunghezza del programma. Quando p viene inserito in A si ottiene il risultato x rappresentato da una sequenza finita di simboli di un qualunque alfabeto. La lunghezza del più corto tra tutti i programmi che danno il risultato x viene chiamata ‛complessità di x relativa ad A', e la indichiamo con K_A (x). Kolmogorov ha dimostrato che esiste un calcolatore universale per cui tale quantità ha un minimo K (x) che chiameremo ‛complessità di x'.

Per definire la complessità di una traiettoria si considera una partizione di M e la sequenza ottenuta registrando gli elementi della partizione da essa visitati in successione (dinamica simbolica). Si calcola la complessità di Kolmogorov dei segmenti di lunghezza n della sequenza, si divide per n, si passa al limite per n → ∞ e si prende l'estremo superiore rispetto alle partizioni. Brudno ha dimostrato che sotto condizioni molto generali la quantità che così si ottiene è uguale all'entropia per quasi tutte le traiettorie. In tal modo si stabilisce un legame tra la caoticità ‛geometrica' delle singole traiettorie e le proprietà statistiche del sistema.

6. Stabilità strutturale

Vogliamo dare una definizione più precisa del concetto di stabilità strutturale discusso in modo informale nell'introduzione. Consideriamo sistemi dissipativi come quelli descritti nel cap. 5, § b. Diremo che il diffeomorfismo ϕ è ‛strutturalmente stabile' se esiste un suo intorno U tale che considerato un elemento ψ ∈ U è possibile stabilire una corrispondenza biunivoca tra le orbite di ϕ e quelle di ψ; tale corrispondenza deve essere data da un omeomorfismo (trasformazione continua insieme alla sua inversa) prossimo all'identità. Affinché questa definizione abbia senso occorre precisare il significato di intorno, cioè la topologia nello spazio dei diffeomorfismi. Una definizione naturale è la seguente: due diffeomorfismi di classe C^r sono vicini se essi sono vicini con le loro derivate fino all'ordine r per la topologia della convergenza uniforme, cioè per la distanza

Un importante teorema afferma che i sistemi che soddisfano all'assioma A sono strutturalmente stabili sotto alcune ipotesi aggiuntive di carattere tecnico.

La stabilità ‛strutturale' è stata un tema dominante nelle ricerche degli anni sessanta. Recentemente si è affermato un diverso punto di vista, che ritiene la stabilità strutturale un concetto troppo vasto per essere utile in uno studio dettagliato di sistemi interessanti nelle applicazioni. Anziché lavorare nella classe di tutti i diffeomorfismi che posseggono un certo numero di derivate, l'attenzione viene concentrata su famiglie di diffeomorfismi che dipendono da alcuni parametri. In questo ambito è possibile porsi per esempio il problema di come varia la struttura delle orbite al variare dei parametri, cioè il problema delle biforcazioni. In particolare è stato studiato il meccanismo della transizione a un comportamento caotico attraverso le biforcazioni omocline e il carattere tipico di certi attrattori. In questo approccio, per proprietà ‛tipica' si intende una proprietà vera per un insieme di misura (di Lebesgue) positiva nello spazio dei parametri. Tra i risultati significativi vi è il seguente: sia ϕ_μ una famiglia di diffeomorfismi C^∞ dipendenti dal parametro μ e agenti su una superficie. Supponiamo che ϕ₀ abbia un punto di tangenza omoclina, cioè un punto in cui la varietà stabile e la varietà instabile di un punto fisso sono tangenti; allora esiste un insieme E di misura positiva tale che se μ ∈ E, ϕ_μ ha un attrattore strano.

BIBLIOGRAFIA

Alekseev, V. M., Jakobson, M. V., Symbolic dynamics and hyperbolic dynamic systems, in ‟Physics reports", 1981, LXXV, 5, pp. 287-325.

Andronov, A. A., Vitt, A. A., Khaikin, S. E., Theory of oscillators, Oxford 1966.

Birkhoff, G. D., Dynamical systems, Providence, R. I., 1927.

Boldrighini, C., Macroscopic limits of microscopic systems, in ‟Rendiconti di matematica e delle sue appplicazioni", 1996, XVI, 1, pp. 1-107.

Cornfeld, I. P., Fomin, S. V., Sinai, Ya. G., Ergodic theory, New York 1982.

Dobrushin, R. L., A mathematical approach to foundations of statistical mechanics, in Boltzmann's legacy. 150 years after his birth, Atti dei Convegni Lincei n. 131, Roma 1997, pp. 227-243.

Dobrushin, R. L., Sinai, Ya. G., Sukhov, Y. M., Dynamical systems of statistical mechanics, in Ergodic theory with applications to dynamical systems and statistical mechanics (a cura di Ya. G. Sinai), New York 1989, pp. 208-254.

Guckenheimer, J., Holmes, P., Nonlinear oscillations, dynamical systems and bifurcations of vector fields, New York 1983.

Laskar, J., Large scale chaos and marginal stability in the solar system, in XI International congress of mathematical physics. Paris 18-21 July 1994 (a cura di D. Iagolnitzer), Cambridge, Mass., 1995, pp. 75-120.

Moser, J., Stable and random motions in dynamical systems: with special emphasis on celestial mechanics, Princeton, N. J., 1973.

Nitecki, Z., Differentiable dynamics: an introduction to the orbit structure of diffeomorphisms, Cambridge, Mass., 1971.

Palis, J., Takens, F., Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations, Cambridge-New York 1993.

Pesin, Y. B., General theory of hyperbolic dynamical systems, in Ergodic theory with applications to dynamical systems and statistical mechanics (a cura di Ya. G. Sinai), New York 1989, pp. 108-151.

Poincaré, H., Les méthodes nouvelles de la mécanique céleste, 3 voll., Paris 1892-1899.

Ruelle, D., Formalisme thermodynamique, in Lecture notes in mathematics (a cura di A. Dold e B. Eckmann), Berlin-New York 1975, pp. 154-166.

Ruelle, D., Hasard et chaos, Paris 1991.

Shub, M., Stabilité globale des systèmes dynamiques, in ‟Astérisque", 1978, n. 56, monografico.

Risultati recenti

SOMMARIO: 1. La nozione di sistema dinamico. Esempi fondamentali: a) i principali tipi di sistemi dinamici; b) esempi classici.  2. Teoria topologica dei sistemi dinamici.  3. Teoria dei sistemi dinamici differenziabili: a) comportamento limite; sistemi integrabili; teoria KAM; b) punti iperbolici e strutture collegate; comportamento stocastico; c) sistemi di Anosov e sistemi che soddisfano all'assioma A di Smale; d) teoria delle biforcazioni; e) metodi analitici.  4. Teoria ergodica dei sistemi dinamici. □ Bibliografia.

1. La nozione di sistema dinamico. Esempi fondamentali

La nozione generale di sistema dinamico è molto ampia. Solitamente i matematici indicano col nome di ‛sistema dinamico' (SD) gruppi o semigruppi di trasformazioni che descrivono diversi processi di evoluzione. Gli spazi nei quali queste trasformazioni agiscono sono detti ‛spazi delle fasi', e nel seguito verranno indicati con M. I parametri del gruppo o del semigruppo sono solitamente detti ‛variabili temporali': tali variabili possono essere più complesse del tempo ordinario, come ad esempio nel caso dei gruppi a molti parametri, dei gruppi liberi, dei gruppi di Lie, ecc. In questo articolo tratteremo solamente il caso dei gruppi o dei semigruppi di trasformazioni a un parametro, anche se faremo riferimenti occasionali a situazioni più generali. Più essenziale è la differenza tra gruppi e semigruppi discreti, cioè numerabili, e gruppi continui. I SD con tempo discreto sono detti omeomorfismi, diffeomorfismi, automorfismi, endomorfismi, cascate o mappe iterate, a seconda del tipo di struttura addizionale aggiunta allo spazio delle fasi e alla trasformazione, mentre i SD con tempo continuo sono solitamente detti flussi o semiflussi.

La teoria dei SD è parte integrante della matematica. Allo stesso tempo i SD sono fondamentali per lo studio di molti problemi di fisica (instabilità, turbolenze, caos deterministico, caos quantistico, per citare solo alcuni dei molti esempi possibili), di ingegneria (controllo ottimale, regolazione), di chimica (reazione di Belousov-Chabotinsky), ecc. Nel seguito descriveremo alcuni tra i più importanti generi di SD e proporremo alcuni esempi.

a) I principali tipi di sistemi dinamici.

1. SD ed equazioni differenziali ordinarie. - Consideriamo un sistema di equazioni differenziali ordinarie:

Solitamente si suppone che le funzioni f_i siano sufficientemente regolari di modo che per ogni condizione iniziale x (0) = (x₁ (0), ..., x_n (0)) esista una e una sola soluzione x (t) = (x₁ (t), ..., x_n (t)) della (1) per - ∞ 〈 t 〈 ∞. In tal caso si può introdurre la trasformazione T^t, definita da T^t x (0) = x (t); risulta chiaro che T^t T^s = T^t+s. Lo spazio delle fasi per {T^t} è Rⁿ; queste {T^t} costituiscono una delle classi più importanti di SD.

Si ottiene una generalizzazione immediata sostituendo la (1) con un campo vettoriale differenziabile su di una varietà differenziabile e introducendo il gruppo delle trasformazioni generate dalle traslazioni lungo le curve integrali del campo vettoriale. In molti casi le funzioni f_i del campo vettoriale dipendono da uno o più parametri. Lo studio della dipendenza della dinamica da questi parametri è un problema importante nella teoria dei SD e verrà trattato nel cap. 3.

2. SD gradiente. - In questo caso il membro di destra della (1) f = (f₁, ..., f_n) è il gradiente di una funzione F (x₁, ..., x_n), cioè

3. Sistemi hamiltoniani. - Sono casi particolari di SD originati da un sistema di equazioni differenziali ordinarie (EDO), con diverse caratteristiche peculiari. Nei sistemi hamiltoniani n = 2 m, le variabili sono dette ‛coordinate' q₁, ..., q_m e ‛impulsi' p₁, ..., p_m, ed m è il numero di gradi di libertà. La dinamica è determinata da una funzione hamiltoniana H (q, p, t) e la (1) diventa

Una possibile generalizzazione della (2) è data dai campi vettoriali hamiltoniani su una varietà simplettica o canonica (v. Arnold, 1989²). I SD hamiltoniani sono il principale oggetto di studio della meccanica classica.

4. Flussi geodetici. - Questa è una classe speciale di sistemi canonici hamiltoniani che evidenzia le profonde connessioni esistenti tra la teoria dei SD, la geometria differenziale e la topologia. Lo spazio delle fasi M è composto dai vettori unitari tangenti a una varietà riemanniana Q detta ‛spazio delle configurazioni'; la trasformazione T^t rappresenta lo spostamento di una distanza t lungo la geodetica determinata dal vettore tangente iniziale x. Talvolta i matematici dicono che il flusso geodetico corrisponde al moto libero su una varietà riemanniana.

5. SD di origine algebrica. - In molte situazioni la dinamica può avere simmetrie addizionali. In tal caso anche lo spazio delle fasi ha delle simmetrie addizionali, come ad esempio quando si tratta di un gruppo di Lie o di uno spazio omogeneo di gruppi di Lie. I gruppi di trasformazioni corrispondenti a SD di questo tipo devono rispettare la simmetria dello spazio delle fasi commutando con le operazioni del gruppo.

6. SD e teoria dei numeri. - Uno dei primi collegamenti tra la teoria dei SD e la teoria dei numeri è apparso in un articolo di H. Weyl (v., 1916), nel quale veniva studiato il problema dell'uniformità della distribuzione della parte frazionaria dei polinomi, cioè della distribuzione in [0, 1] dei numeri x_n = {a₀ + a₁ n + a₂ n² + ... + a_r n^r}, dove a₀, a₁, ..., a_r sono numeri reali dati, 0 ≤ n ≤ ∞ e {•} indica la parte frazionaria. Si ricordi che una successione x_n è uniformemente distribuita su [0, 1] se per ogni funzione continua f

In molti casi la successione {x_n} può essere rappresentata come una successione di valori di una funzione differenziabile lungo orbite di SD. Solitamente, come abbiamo già detto, i sistemi dinamici in questione possiedono simmetrie addizionali.

Anche altri problemi asintotici in teoria dei numeri sono stati connessi, in maniera analoga, a problemi di teoria dei SD. In questo campo, H. Furstenberg e i suoi collaboratori hanno ottenuto molti risultati importanti con l'aiuto della teoria dei SD (v., ad esempio, Furstenberg, 1981).

7. Dinamica olomorfa. - Uno dei più noti sistemi dinamici con tempo discreto è la trasformazione (o map) quadratica x → ax (1 - x), 0 ≤ x ≤ 1, solitamente interpretata nei termini del problema ‛preda-predatore'. Il valore di x è considerato come una densità di predatori, mentre (1 - x è la densità di prede; quella in esame è una trasformazione che descrive in maniera molto generale il cambiamento nella composizione della popolazione da una generazione alla successiva. Il parametro a è arbitrario; in generale i fenomeni più interessanti si verificano per a > 1. Per piccoli x le prede costituiscono la parte dominante del sistema; i predatori hanno quindi un terreno favorevole per crescere di numero e, di conseguenza, alla generazione successiva la densità di predatori aumenta. Se x è vicino a uno, la quantità di cibo disponibile non è sufficiente e il numero dei predatori diminuisce nuovamente. In generale si osservano orbite oscillanti in maniera irregolare, pur trattandosi di un sistema deterministico.

La famiglia delle trasformazioni quadratiche ha un ruolo importante nella teoria dei SD (v. sotto, punto 8). La semplicità delle formule che descrivono la dinamica permette di effettuare facilmente analisi numeriche dirette di questi SD. Questa semplicità è però solo apparente, in quanto per molti valori di a le traiettorie possono essere assai complesse e, apparentemente, del tutto caotiche: esse possono cioè sembrare una tipica realizzazione di un processo casuale. La famiglia delle trasformazioni quadratiche è pertanto tutt'altro che banale; a questo proposito sono stati ottenuti numerosi risultati interessanti (v., per esempio, de Melo e van Strien, 1993).

Se si ammettono anche i valori complessi di x, si può considerare x → ax (1 - x) come una trasformazione nel piano complesso. In maniera più generale si possono studiare le trasformazioni x → P (x), dove P è un polinomio o un rapporto tra polinomi. Per esempio, nel metodo di Newton per trovare le radici dei polinomi P (x) = 0 si incontra la trasformazione x →

I primi risultati sulle trasformazioni del tipo x →

sono stati ottenuti da Julia (v., 1918) e da Fatou (v., 1919-1920). Attualmente, la teoria di queste trasformazioni rappresenta una delle parti più affascinanti e più intensamente studiate della teoria dei SD.

8. SD e teoria della probabilità. - Talvolta si studiano SD con forze o coefficienti casuali, come ad esempio:

dove η_i (t, x) = η_i (t) è un rumore casuale. Su queste equazioni è stata costruita una elegante teoria, con molte applicazioni, anche se la (3) non è strettamente un SD nel senso definito sopra, bensì un insieme statistico di SD, data la presenza di rumore casuale. Per questo motivo non discuteremo questo problema nel seguito.

Esiste anche un diverso tipo di collegamento tra la teoria dei SD e la teoria della probabilità. Supponiamo di avere uno spazio Ω di funzioni campione ω (t) di qualche processo casuale, con tempo discreto o continuo. Indichiamo con P la distribuzione di probabilità corrispondente. Se t ∈ Z⁺, Z o R⁺, R possiamo introdurre il semigruppo o il gruppo delle trasformazioni {T^s} di Ω, dove (T^s ω) (t) = ω (t + s), s ∈ Z⁺, Z o R⁺, R. Se la distribuzione di probabilità P è conservata sotto l'azione di questo gruppo di trasformazioni (v. cap. 4), il nostro processo casuale è stazionario. Secondo la definizione data precedentemente, il gruppo - o il semigruppo - di trasformazioni su Ω che ne deriva è un caso particolare di SD: esempi tipici sono le sequenze di variabili casuali indipendenti distribuite in maniera identica (traslazioni, o shifts, di Bernoulli), le catene di Markov (traslazioni di Markov), i processi stazionari gaussiani, ecc.

9. Alcuni SD con tempo a molte dimensioni. - Il tempo unidimensionale corrisponde a un SD che descrive un'evoluzione con una ‛freccia del tempo'. In fisica statistica, in fisica dello stato solido e nella teoria dei campi quantistici si trovano invece esempi tipici di SD con tempo a molte dimensioni in cui i relativi gruppi di trasformazioni sono i gruppi delle traslazioni spaziali e delle traslazioni spazio-temporali. Un modello ben noto, ad esempio, descrive i magneti basandosi su uno spazio delle fasi consistente in tutte le possibili configurazioni ϕ (x), dove x è un punto nel reticolo cristallino e ϕ (x) la variabile di spin in x. Il gruppo sottostante è il gruppo di tutte le traslazioni sul cristallo. In maniera del tutto analoga i campi quantistici nella teoria dei campi sono funzioni ϕ (x, tP) dello spazio e del tempo; il gruppo corrispondente è il gruppo delle traslazioni spazio-temporali.

b) Esempi classici.

Alcuni esempi concreti di sistemi dinamici hanno costituito delle pietre miliari nello sviluppo di alcune parti della teoria matematica omonima. Citiamo, in primo luogo, la trasformazione standard (o di Chirikov, o di Chirikov-Taylor), che è una trasformazione di un cilindro bidimensionale. Scegliamo le coordinate z, ϕ, dove z è l'ampiezza e ϕ la fase. La trasformazione T è data da T : (z, ϕ) → (z′, ϕ′), dove z′ = z + k sen 2 πϕ, ϕ′ = ϕ + z′ (mod 1); k è un parametro. Si possono considerare classi più generali di funzioni periodiche invece di limitarsi al solo seno: in questo modo si può arrivare all'insieme delle cosiddette trasformazioni torcenti (twist maps). Negli anni ottanta Aubry (v., 1983) e Mather (v., 1982) hanno ottenuto alcuni risultati importanti nella teoria delle trasformazioni torcenti. La trasformazione standard è uno dei primi esempi (v. Lichtenberg e Lieberman, 1983) nella teoria del caos hamiltoniano (v. Chirikov, 1979; v. Moser, 1968).

Il ‛sistema di Lorenz' è un famoso sistema di equazioni differenziali ordinarie. Tale sistema - ottenuto da Lorenz come approssimazione di Galerkin a un sistema di equazioni alle derivate parziali di tipo idrodinamico e apparso per la prima volta in un articolo del 1963 - è della forma:

dove σ, r, b sono parametri numerici. L'importanza di questo sistema è molto aumentata negli anni settanta, quando i matematici hanno iniziato a studiarlo, in particolar modo in collegamento con il concetto di attrattore strano introdotto da Ruelle e Takens (v., 1971).

La ‛trasformazione di Hénon' è una trasformazione bidimensionale (x, y) → (1 + y - ax², bx) dipendente da due parametri a e b, introdotta da Hénon (v., 1976) come versione discreta del sistema di Lorenz. In effetti, le sue proprietà sono da molti punti di vista diverse da quelle del sistema di Lorenz. I primi risultati matematicamente rilevanti sono stati ottenuti da Benedicks e Carleson (v., 1991). Questa trasformazione contiene molte delle cosiddette biforcazioni tangenti (v. Newhouse, 1974), e attualmente essa e le sue generalizzazioni sono oggetto di intenso lavoro.

Infine, i ‛biliardi' sono sistemi dinamici che corrispondono al moto libero di un punto materiale all'interno di domini di Rⁿ, con collisioni elastiche sul bordo. I sistemi a molti corpi con interazioni generali e con collisioni elastiche tra le particelle possono essere descritti come biliardi modificati. Le proprietà dinamiche e statistiche dei biliardi sono determinate principalmente dalla forma del bordo (v. Cornfeld e altri, 1982).

Ci sono anche molti esempi importanti di SD a infinite dimensioni. Pensando ad esempio all'idrodinamica, consideriamo un sistema di equazioni di Navier-Stokes che descrive il moto di un liquido viscoso incomprimibile in un dominio limitato. Lo spazio delle fasi è composto da tutti i campi vettoriali a divergenza nulla definiti in questo dominio e, chiaramente, ha dimensione infinita. Il sistema di Navier-Stokes genera un gruppo, o un semigruppo, di trasformazioni su questo spazio. Considerando le componenti delle velocità rispetto a una qualche base ortogonale, si può trasformare il sistema di Navier-Stokes in un sistema di equazioni differenziali ordinarie a dimensione infinita. Poiché le soluzioni delle equazioni di Navier-Stokes sono continue e addirittura differenziabili, i coefficienti con indice grande dovrebbero restare piccoli durante l'evoluzione e l'importanza dei diversi gradi di libertà dovrebbe diminuire al crescere dell'indice. Altri tipi di SD con spazi delle fasi a dimensione infinita, o comunque molto grande, sono ad esempio i sistemi a molti corpi interagenti con potenziali di coppia; in tutti questi sistemi i diversi gradi di libertà sono equivalenti o comunque hanno un ruolo simile nella dinamica. Le teorie di questi due tipi di SD di dimensione infinita sono piuttosto diverse.

2. Teoria topologica dei sistemi dinamici

In molti casi risulta naturale supporre che lo spazio delle fasi M sia uno spazio topologico completo e che il semigruppo o il gruppo delle trasformazioni che determinano la dinamica consista di trasformazioni continue, oppure continue e invertibili. La parte della teoria dei SD basata esclusivamente su queste ipotesi è detta ‛dinamica topologica' e studia le proprietà dei SD che restano invariate rispetto a un cambio di variabili continuo. Per questo è naturale porre la definizione seguente: siano {T1^t} e {T2^t} due SD agenti sullo stesso spazio delle fasi M; essi sono detti ‛topologicamente coniugati' se si può trovare un omeomorfismo ϕ : M → M tale che T1^t = ϕ^-1 T2^t ϕ.

Le definizioni seguenti stabiliscono le proprietà rilevanti al riguardo. Un punto x è detto periodico se T^t x = x per qualche t > 0. Il minimo t con questa proprietà è detto periodo di x. L'intera orbita {T^t x} è pure detta periodica. Se T^t x = x per ogni t, allora x è un punto fisso. Un punto x viene detto + ricorrente (o - ricorrente) se per ogni intorno U, x ∈ U esistono dei t arbitrariamente grandi tali che T^t x ∈ U (o T^-t x ∈ U se T^-t è definita).

Un SD {T^t} è ‛minimale' se la chiusura di ogni orbita −{−T−^t −x−} coincide con M. La minimalità è equivalente all'assenza di sottoinsiemi chiusi invarianti non banali. Un SD è detto ‛topologicamente transitivo' se esiste un x ∈ M per cui −{−T−^t −x−} = M. Un SD è detto ‛topologicamente mescolante' (mixing) se per ogni coppia di sottoinsiemi aperti A, B ⊂ M esiste un t₀ tale che A ⋂ T^t B ≠ 0/ per ogni t > t₀.

Risulta chiaro che la presenza o l'assenza di punti periodici, di punti ricorrenti, di minimalità, di transitività topologica e di mescolamento sono invarianti topologici, cioè tali proprietà non cambiano sotto coniugazione topologica. La dinamica topologica è stata molto studiata negli anni venti e trenta. Poiché in seguito si è capito che la nozione di coniugazione topologica era troppo restrittiva, essa è stata sostituita dalla seguente definizione: due sistemi dinamici {T₁^t} e {T2^t} sono topologicamente equivalenti se esiste un omeomorfismo ϕ : M → M tale che, per ogni x ∈ M, ϕ ({T1^t x}) = {T2^t ϕ (x)}. In altre parole, ϕ trasforma le traiettorie del primo SD in quelle del secondo, ma il moto lungo le traiettorie può essere diverso. Se il tempo è discreto e lo spazio delle fasi è connesso, le definizioni di equivalenza topologica e di coniugazione topologica sono equivalenti. Talvolta si dice che SD topologicamente equivalenti hanno la stessa struttura nello spazio delle fasi.

Consideriamo ora la nozione di stabilità strutturale, introdotta dal fisico russo A. A. Andronov: un SD {T^t} è detto strutturalmente stabile o robusto se ogni SD {T1^t} sufficientemente vicino a {T^t} è topologicamente equivalente a {T^t}, con ϕ vicina alla trasformazione identica. I primi teoremi matematici a tal proposito, unitamente a una precisa formulazione matematica di questa proprietà, furono pubblicati in un lavoro di Andronov e Pontryagin (v., 1937). In particolare questi autori mostrarono che SD generici corrispondenti a equazioni differenziali ordinarie del tipo (1) all'interno di un cerchio sono strutturalmente stabili. In seguito questo risultato è stato esteso da Peixoto (v., 1962) a tutti i SD generati da campi vettoriali su superfici chiuse bidimensionali. Una conclusione generale ottenuta dai risultati di questi due lavori è che un generico sistema bidimensionale di equazioni differenziali ordinarie, ad esempio del tipo (1) con n = 2, possiede un numero finito di punti fissi o di traiettorie periodiche; le altre traiettorie tendono a uno di essi quando t → ± ∞.

Per molti anni si è cercato di estendere queste affermazioni a spazi delle fasi multidimensionali, ma in questo caso la situazione si è rivelata più complessa. Per esempio, esistono SD strutturalmente stabili con un numero infinito di traiettorie periodiche; inoltre, dato uno spazio delle fasi arbitrario, l'insieme dei SD strutturalmente stabili non è denso nello spazio di tutti i SD agenti su di esso. I primi risultati importanti a questo proposito sono dovuti a Anosov (v., 1969) e a Smale (v., 1967), e verranno discussi nel cap. 3.

Anche nel caso multidimensionale esiste però una classe di SD strutturalmente stabili il cui comportamento assomiglia a quello dei sistemi bidimensionali, cioè i cosiddetti sistemi di Morse-Smale (v. Sinai, 1972), nei quali ogni traiettoria tende a una traiettoria periodica o a un punto fisso; l'insieme di tali traiettorie periodiche è finito e ciascuna di esse è iperbolica (v. cap. 3). Un esempio importante è dato dai sistemi gradiente (v. cap. 1, § a, punto 2): in questo contesto i sistemi strutturalmente stabili sono quelli derivati da funzioni generiche, o di Morse.

Sempre intorno alla metà degli anni sessanta è apparsa la nozione di entropia topologica, che è un altro invariante topologico collegato a quanto appena discusso e ad altri sviluppi contemporanei nella teoria dei SD. La definizione di entropia topologica, introdotta da Adler, Conheim e McAndrew (v., 1965), è stata successivamente modificata e adesso viene usualmente formulata nella maniera seguente: supponiamo che lo spazio delle fasi M sia metrico e compatto, con metrica d, e che T : M → M sia una trasformazione continua; per ogni n > 0 introduciamo una nuova metrica d_n (x, y) = max_{0≤ i ≤ n} d (Tⁱ x, Tⁱ y); sia N (n, T, ε) il minimo numero di intorni sferici di raggio ε, nella metrica d_n, che ricoprono M. Allora

Una definizione analoga può essere data per SD con tempo continuo. Il numero h (T) è detto ‛entropia topologica' e ha il significato di una misura della crescita del numero di diversi tipi di traiettorie. Se M ha dimensione finita, allora h (T) 〈 ∞. Nei SD con comportamento iperbolico si trova entropia positiva h > 0 (v. capp. 3 e 4). La dinamica nei sistemi con entropia topologica positiva è considerata ‛complessa'.

3. Teoria dei sistemi dinamici differenziabili

In questo capitolo supporremo che M sia una varietà di classe C^r di dimensione finita e che i SD siano iterazioni di una trasformazione differenziabile T^t = (T)^t, t ∈ Z⁺ o Z, oppure che essi siano traslazioni lungo soluzioni di un sistema di equazioni differenziali ordinarie, dato dalla (1), o campi vettoriali.

La classe di differenziabilità r determina una topologia nello spazio dei SD da cui dipendono alcune proprietà e alcuni risultati. Una proprietà di un SD è detta ‛generica' se è condivisa da tutti i SD che appartengono a un'intersezione numerabile di sottoinsiemi aperti densi nell'intero spazio dei SD considerati. Questa è la nozione standard usata per definire un comportamento tipico nella teoria dei SD. Esempi di proprietà generiche (nel caso di spazio delle fasi compatto) sono, ad esempio, il numero finito di punti fissi, l'assenza di famiglie continue di orbite periodiche, ecc. Bisogna inoltre sottolineare che la nozione di genericità dipende dallo spazio dei SD considerati. Per esempio, i sistemi hamiltoniani sono non generici nello spazio di tutti i SD, ma si possono comunque considerare proprietà generiche nello spazio dei sistemi hamiltoniani.

a) Comportamento limite; sistemi integrabili; teoria KAM.

Ciascun SD o, meglio, ciascuna evoluzione ha la sua freccia del tempo. Con questo intendiamo dire che, nel caso di spazi compatti M, ciascuna traiettoria ha un ‛comportamento limite' quando t → ∞. Quando una traiettoria ha raggiunto questo regime, essa oscilla nel tempo, ma il comportamento delle medie temporali è stabile. Concetti simili possono essere applicati a spazi delle fasi non limitati, ma non discuteremo questo aspetto.

L'avvicinamento a un regime limite può spesso essere descritto con l'aiuto delle funzioni di Lyapunov. Una funzione L (x) è detta ‛funzione di Lyapunov' se L (T^t x) è, per ogni x fissato, una funzione monotona decrescente di t. Allora il regime limite citato in precedenza corrisponde alla parte dello spazio delle fasi in cui L raggiunge il suo minimo. Nei sistemi gradiente le funzioni generatrici F sono allo stesso tempo funzioni di Lyapunov; talvolta, tuttavia, queste ultime possono essere costruite anche per sistemi dissipativi di equazioni differenziali ordinarie, nei quali

〈 0 (sostituita da un'analoga disuguaglianza per tempi discreti). La parte di spazio delle fasi corrispondente al regime limite può talvolta essere decomposta in sottoinsiemi invarianti più piccoli. Solitamente questo è fatto con l'aiuto della nozione di ‛integrale primo'. Una funzione I (x) è detta integrale primo se I (T^t x) = I (x) per ogni t. Nella teoria dei SD differenziabili si suppone che I sia differenziabile o almeno continuo, mentre nella teoria ergodica dei SD, basata sulla teoria della misura, è sufficiente che la funzione I sia misurabile (v. cap. 4).

Se un SD possiede k integrali primi I₁, I₂, ..., I_k, allora ogni sottoinsieme I₁ = costante₁, I₂ = costante₂, ..., I_k = costante_k è invariante rispetto alla dinamica, cioè è composto di traiettorie. Esiste inoltre la non ben definita nozione di ‛sistema integrabile': essa caratterizza più o meno i sistemi in cui, dopo avere fissato il valore di tutti gli integrali primi, la dinamica sui sottoinsiemi invarianti ottenuti può essere completamente descritta per mezzo di funzioni elementari o con altri metodi.

La nozione di sistema integrabile è importante nella dinamica hamiltoniana (v. eq. 2). Ricordiamo a questo proposito il teorema di Arnold-Liouville (v. Arnold, 1989²), il quale afferma che se un sistema hamiltoniano con m gradi di libertà possiede m integrali primi indipendenti che sono in involuzione, cioè

per ogni k₁, k₂, e l'insieme {(p, q) ∣I_k} = costante_k, 1 ≤ k ≤ m è compatto, allora esso è un toro m-dimensionale e il moto sul toro è quasi-periodico, cioè può essere descritto tramite funzioni quasi-periodiche del tempo.

La dinamica hamiltoniana fornisce numerosi esempi di sistemi hamiltoniani integrabili. Circa trent'anni fa è stato scoperto un metodo efficace per determinare nuove classi di sistemi hamiltoniani integrabili, basato sulla cosiddetta tecnica dello scattering inverso. I primi risultati a questo proposito sono stati ottenuti da Kruskal, Zabusky, Miura, Gardner, Zakharov, Shabat e altri (v., ad es., Olver e Sattinger, 1990). Tra gli esempi concreti cui questo metodo può essere applicato ricordiamo l'equazione fisicamente rilevante di Korteweg-de Vries, l'equazione di Schrödinger non lineare, i cosiddetti sistemi di Moser-Calogero, i reticoli di Toda, ecc.

Sicuramente i sistemi integrabili devono essere considerati come eccezionali. Risulta pertanto importante studiare la struttura delle loro piccole perturbazioni; questo - secondo Poincaré - è il problema più importante della dinamica. Oltre trent'anni fa è stata formulata la famosa teoria di Kolmogorov-Arnold-Moser (KAM), la quale afferma che, per piccole perturbazioni rispetto ai cosiddetti sistemi hamiltoniani integrabili non degeneri, lo spazio delle fasi contiene un sottoinsieme grande (nel senso della teoria della misura) composto da tori m-dimensionali invarianti riempito da traiettorie quasi periodiche. La dimostrazione sfrutta una versione del metodo di Newton sulla cui base si può costruire una teoria delle perturbazioni che permette di estrarre dei tori separati. Risulta essenziale il fatto che l'insieme dei tori invarianti che sopravvivono sotto la perturbazione non è un dominio, ma un sottoinsieme di misura positiva con molti buchi. In seguito la teoria KAM è stata estesa a molte altre classi di SD integrabili; essa ha un gran numero di applicazioni nella dinamica hamiltoniana stessa, nella meccanica celeste, nella fisica dei plasmi, ecc. (v. Kolmogorov, 1957; v. Moser, 1968; v. Arnold, 1963 e 1993).

L'esempio più utile per comprendere la teoria KAM e la sua importanza è la trasformazione standard con le sue generalizzazioni, le trasformazioni torcenti (v. cap. 1, § b). Le sue proprietà dipendono da k o, in altre parole, dalla piccolezza della funzione che la definisce. Per k piccoli la teoria KAM garantisce l'esistenza di un insieme di misura positiva formato da curve invarianti che racchiudono il toro. Su ciascuna curva la trasformazione può essere scritta, nelle coordinate appropriate, come una rotazione. Argomenti generali (v., ad es., Sinai, 1994) mostrano che per k grandi non esistono curve di tale tipo. Aubry (v., 1983) e Mather (v., 1982) hanno mostrato che al crescere di k le curve KAM non spariscono completamente. Esse si biforcano in insiemi invarianti, non densi in alcun punto (gli insiemi di ‛Aubry-Mather', talvolta detti ‛cantori', seguendo Percival). Il moto su di essi è ristretto a pure rotazioni, ma la riduzione è fatta tramite funzioni discontinue. La distruzione delle curve KAM è una delle più interessanti tra le biforcazioni scoperte negli ultimi anni.

Se si considera una trasformazione differenziabile con una curva invariante, oppure un sistema di equazioni differenziali ordinarie bidimensionale (eq. 1 con n = 2) nel quale f₁ e f₂ sono funzioni periodiche, l'analisi della dinamica può essere spesso ridotta allo studio delle trasformazioni differenziabili o dei diffeomorfismi sul cerchio S¹. I primi risultati nello studio di queste trasformazioni sono dovuti a Poincaré e ad A. Denjoy (v. Coddington e Levinson, 1955). In particolare, essi hanno introdotto la nozione di ‛numero di rotazione', cioè del valor medio della rotazione per ogni applicazione della mappa. Un ben noto risultato di Denjoy dice che per trasformazioni C² e numeri di rotazione irrazionali il diffeomorfismo può essere scritto, nelle coordinate appropriate, come una rotazione. Il teorema di Denjoy serve soltanto a garantire l'esistenza delle coordinate nelle quali esso è scritto come una rotazione; risulta naturale chiedersi come questo cambio di variabili dipenda dalle proprietà della trasformazione (problema talvolta detto ‛di Arnold'). Il risultato principale a questo proposito è stato ottenuto da Herman (v., 1979) e consiste nel fatto che per numeri di rotazione tipici e diffeomorfismi di classe C^r la riduzione può essere fatta tramite un cambio di variabili di classe C^r-1 (l'affermazione del teorema di Herman è in realtà più forte). Una dimostrazione più breve è stata trovata da J. C. Yoccoz. Recentemente sono apparse nuove dimostrazioni basate sulle idee della teoria del gruppo di rinormalizzazione (v. Sinai, 1994).

b) Punti iperbolici e strutture collegate; comportamento stocastico.

In questo paragrafo e nel successivo discuteremo alcuni tipi di comportamento dinamico più complicati, solitamente associati con la nozione di caos deterministico.

Iniziamo con un tempo discreto. Consideriamo un punto periodico x⁽⁰⁾, cioè tale che T^k x⁽⁰⁾ = x⁽⁰⁾, dove k è il periodo. Supponiamo di scegliere in un intorno di x⁽⁰⁾ un sistema di coordinate tale che x⁽⁰⁾ sia l'origine e T^k sia dato da n funzioni differenziabili y = (y₁, ..., y_n) = T^k x = T^k (x₁, ..., x_n), cioè y_i = ϕ_i (x₁, ..., x_n), 1 ≤ i ≤ n. Dal momento che x⁽⁰⁾ è un punto fisso rispetto a T^k, si ha ϕ_i (0, ..., 0) = 0. Consideriamo adesso la matrice di Jacobi dT_x⁽⁰⁾ =

Un punto x⁽⁰⁾ viene detto ‛iperbolico' se nessuno degli autovalori di dT_x⁽⁰⁾ ha valore assoluto uguale a 1.

Talvolta la matrice di Jacobi di un punto iperbolico è detta anch'essa iperbolica. È ben noto dall'algebra lineare che nel caso di matrici iperboliche lo spazio Rⁿ può essere rappresentato come la somma di due sottospazi lineari Rⁿ = L^(s) + L^(u), dove dim L^(s) (dim L^(u)) è uguale al numero, molteplicità comprese, di autovalori con valore assoluto minore (maggiore) di 1, ed esistono due costanti positive A 〈 ∞, λ 〈 1 tali che

L'esistenza di spazi analoghi a questi sottospazi invarianti è utilizzata nella definizione di traiettorie iperboliche generali. Consideriamo infatti un qualsiasi punto x⁽⁰⁾ e i sottospazi T_x(i) tangenti a M nei punti x⁽ⁱ⁾ = Tⁱ x⁽⁰⁾. Senza perdita di generalità possiamo supporre che ciascun T_x sia dotato di un'adeguata norma. Ogni applicazione T determina una trasformazione naturale dT: T_x → T_Tx, detta ‛trasformazione di Jacobi'. Come sopra, in coordinate locali (x₁, ..., x_n) intorno ad x e (y₁, ..., y_n) intorno a T_x essa è data dalla matrice

= dT_x.

Un punto x⁽⁰⁾ è detto iperbolico (oppure uniformemente iperbolico) se esistono delle costanti positive A 〈 ∞, λ 〈 1, ε₀ > 0 e una decomposizione di ciascuno spazio tangente T_x(i) = L_x^(s)_(i) + L_x^(u)_(i) per x⁽ⁱ⁾ = Tⁱ x⁽⁰⁾, - ∞ 〈 i 〈 ∞, tali che

Chiaramente, dim L_x^(s)_(i) e dim L_x^(u)_(i) non devono dipendere da i. Spesso è necessario considerare traiettorie che soddisfino condizioni meno stringenti, permettendo, ad esempio, che l'angolo tra i sottospazi L_x^(s)_(i), L_x^(u)_(i) sia piccolo e che la costante A dipenda da m. In tali casi x⁽⁰⁾ è detto punto non uniformemente iperbolico.

La proprietà più importante dei punti iperbolici è l'esistenza di varietà locali stabili e instabili, data dal famoso teorema di Hadamard-Perron, secondo il quale dato un qualsiasi punto iperbolico x⁽⁰⁾ esistono delle sottovarietà di classe C^r, γ_x^(s)₍₀₎ e γ_x^(u)₍₀₎, in un piccolo intorno di x⁽⁰⁾, tali che:

1) x⁽⁰⁾ = γ_x^(s)₍₀₎ ⋂ γ_x^(u)₍₀₎;

2) dim γ_x^(s)₍₀₎ = dim L_x^(s)₍₀₎, dim γ_x^(u)₍₀₎ = dim L_x^(u)₍₀₎;

3) esistono valori positivi A₁ 〈 ∞, λ₁ 〈 1 tali che, per ogni m ≥ 0

dist (T^m y, x^(m)) ≤ A₁ λ^m dist (y, x⁽⁰⁾) per ogni y ∈ γ_x^(s)₍₀₎;

dist (T^-m y, x^(-m)) ≤ A₁ λ^m dist (y, x⁽⁰⁾) per ogni y ∈ γ_x^(u)₍₀₎.

La proprietà 3) spiega il significato dei termini varietà ‛localmente stabile', ‛localmente instabile' e ‛comportamento iperbolico'. Infatti, lungo L_x^(s)₍₀₎ (L_x^(u)₍₀₎) la dinamica è stabile in direzione positiva (negativa).

Il teorema di Hadamard-Perron dice che per ogni punto iperbolico x esistono punti y per i quali le semitraiettorie positive (negative) {T^t x, t > 0 ({T^t y, t 〈 0}) convergono alla semitraiettoria positiva (negativa) di x e che la convergenza è esponenziale. Questi punti, vicino a x, costituiscono γ^(s) (γ^(u)). Un comportamento analogo caratterizza le geodetiche sul piano iperbolico, o di Lobachevsky. Questa è la ragione per cui i punti ai quali si applica il teorema di Hadamard-Perron sono detti iperbolici (per una dimostrazione di questo teorema, con alcune osservazioni generali, v. Anosov, 1969; v. anche Hirsch e altri, 1977).

Le varietà ‛globalmente stabili' o ‛instabili' Γ_x^(s)₍₀₎, (Γ_x^(u)₍₀₎) sono definite come quelle composte da punti y tali per cui dist (T^m y, x^(m)) → 0 quando m → ∞ (m → - ∞).

In molti casi l'esistenza dei punti iperbolici e delle strutture a essi collegate implica un qualche tipo di comportamento stocastico. Questo fatto è stato intuito da Poincaré e studiato in modo approfondito da Smale e collaboratori (v. Sinai, 1972 e 1994), da Shilnikov e collaboratori (v. Ruelle, 1978) e da altri.

Consideriamo un dato punto iperbolico x⁽⁰⁾ e le rispettive varietà, stabile e instabile, Γ_x^(s)₍₀₎, Γ_x^(u)₍₀₎. Un punto y è detto ‛punto omoclino' se y ∈ Γ_x^(s)₍₀₎ ⋂ Γ_x^(s)₍₀₎. Se le varietà Γ_x^(s)₍₀₎, Γ_x^(u)₍₀₎ hanno un'intersezione trasversale in y, allora y è detto ‛punto trasversale omoclino'. In quest'ultimo caso l'intersezione delle varietà tangenti a Γ_x^(s)₍₀₎ e Γ_x^(u)₍₀₎ in x_x⁽⁰⁾ è composta soltanto dallo zero. Per un punto omoclino T^m y → x⁽⁰⁾ per m → ± ∞.

Dato ε > 0, si consideri l'insieme S_ε (y) dei punti y le cui traiettorie appartengono all'intorno chiuso di raggio ε della traiettoria di un punto omoclino trasversale T^m y, - ∞ 〈 m 〈 ∞. Ne deriva il seguente teorema: per ogni ε > 0 l'insieme S_ε (y) è non vuoto, chiuso e invariante. Per ε sufficientemente piccolo esso è composto soltanto da punti iperbolici e contiene un sottoinsieme numerabile denso di punti periodici iperbolici.

Smale ha dimostrato questo teorema utilizzando la nozione del ‛ferro di cavallo', da lui introdotta e studiata (v. Smale, 1967). I ferri di cavallo appaiono frequentemente nei SD e possono essere determinati molto facilmente per via numerica. Consideriamo ora un ε sufficientemente piccolo da rendere S_ε (y) iperbolico: l'insieme S_ε (y) è detto ‛strato stocastico'. Questa definizione nasce dal fatto che i punti di S_ε (y) possono essere rappresentati come realizzazioni di un processo casuale (la cosiddetta ‛rappresentazione simbolica'). Nei lavori di Smale, di Shilnikov e di altri citati in precedenza, si trova una descrizione dettagliata di questa rappresentazione. Molto spesso gli strati stocastici sono associati con i ferri di cavallo.

Strati stocastici più complessi possono essere costruiti con l'aiuto dei cosiddetti ‛punti eteroclini'. Sia x⁽⁰⁾ un punto periodico iperbolico: un punto y è detto eteroclino se per un qualche i, y ∈ Γ_x^(s)₍₀₎ ⋂ Γ_x^(u)_(i). Se Γ_x^(s)₍₀₎, Γ_x^(u)_(i) hanno un'intersezione trasversale in y, allora y è detto ‛punto eteroclino trasversale'.

Utilizzando i punti eteroclini trasversali si possono costruire altri tipi di strati stocastici. Arnold ha scoperto alcune forme di instabilità in SD hamiltoniani analizzando l'intersezione di varietà stabili e instabili di traiettorie periodiche o di sottoinsiemi invarianti più complicati. Questa instabilità è detta ‛diffusione di Arnold' (v. Arnold, 1964). Alcuni problemi fisici cui si applica la teoria della diffusione di Arnold sono descritti nella rassegna di Chirikov (v., 1979). Recentemente Sagdeev, Zaslavski e altri hanno costruito dei SD con strati stocastici generati da numerosi punti eteroclini, detti reti stocastiche (v. Zaslavski e altri, 1991). G. Gallavotti ha inoltre studiato la diffusione di Arnold in relazione ad alcuni problemi di meccanica celeste.

Le definizioni principali di iperbolicità, di varietà stabili e instabili, di traiettorie omocline ed eterocline possono essere applicate nella stessa forma ai SD con tempo continuo, cioè ai flussi. Ma in questo caso si suppone che la somma delle dimensioni della varietà stabile e di quella instabile sia n -1, in quanto una dimensione viene lasciata a disposizione per il sottospazio corrispondente ai vettori del campo vettoriale soggiacente al SD.

c) Sistemi di Anosov e sistemi che soddisfano all'assioma A di Smale.

Trent'anni fa Anosov (v., 1969) iniziò lo studio di un'importante classe di SD, successivamente detti ‛sistemi di Anosov'. In questo contesto la definizione è abbastanza semplice: il SD {T^t} su uno spazio compatto M è detto sistema di Anosov se ciascun punto è iperbolico, se la decomposizione degli spazi tangenti T_x = L_x^(s) + L_x^(u) è continua e se le costanti A, λ possono essere scelte in maniera indipendente da x.

I sistemi di Anosov con tempo discreto sono detti ‛diffeomorfismi di Anosov', e quelli con tempo continuo ‛flussi di Anosov'. Tra i principali esempi di sistemi di Anosov vi sono gli automorfismi toroidali, cioè le trasformazioni di tori n-dimensionali della forma seguente:

e le loro perturbazioni non lineari. Un caso particolare piuttosto noto è la cosiddetta ‛trasformazione del gatto di Arnold', che è la trasformazione del toro bidimensionale data dalla matrice

In questo caso la dinamica è connessa con i numeri di Fibonacci. I principali esempi di flussi di Anosov sono il flusso geodetico su varietà compatte di curvatura negativa e le sue perturbazioni. Queste ultime costituiscono un genere di SD molto importante, che connette la teoria dei SD con la teoria delle rappresentazioni dei gruppi e delle forme modulari e con la teoria dei numeri.

Uno dei risultati principali della teoria dei sistemi di Anosov è il teorema, dovuto ad Anosov stesso (v. Anosov, 1969), secondo il quale tali sistemi sono strutturalmente stabili. Alla sua apparizione questo teorema suscitò sorpresa, in quanto nei sistemi di Anosov la dinamica locale vicino a qualsiasi punto è completamente instabile. Limitatamente ad alcuni casi particolari, tuttavia, esso era stato anticipato da R. Thom e da Smale. Inoltre, i sistemi di Anosov hanno altre proprietà, completamente differenti da quelle dei sistemi bidimensionali per i quali la stabilità strutturale era stata dimostrata in precedenza. Una di queste proprietà, talvolta detta ‛transitività' dei sistemi di Anosov, è la seguente: se almeno uno tra Γ_x^(s) e Γ_x^(u) è denso ovunque, allora entrambi sono densi. Inoltre, in un sistema di Anosov transitivo le traiettorie periodiche sono dense ovunque.

I sistemi di Anosov sono stati oggetto di intensi studi. Le loro modificazioni, come ad esempio i sistemi derivati dai sistemi di Anosov, gli pseudo-sistemi di Anosov, ecc., compaiono in molti problemi di topologia e di geometria differenziale.

Smale (v., 1967) ha introdotto una classe di SD più generale, che include i sistemi di Anosov, ora detta dei ‛sistemi che soddisfano all'assioma A': un punto x ∈ M è detto ‛vagante' se esistono un intorno U di x e un tempo t₀ tali che T^t U ⋂ U = 0/ per ogni t ≥ t₀. Gli altri punti sono detti ‛non vaganti' (si confronti questa definizione con quella di punto ricorrente, data nel cap. 2). L'insieme dei punti non vaganti di un SD è indicato con Ω ({T^t}). Esso è chiuso e invariante rispetto alla dinamica. Nell'insieme dei punti non vaganti si possono incontrare molte proprietà interessanti della dinamica. Ma anche il tipo di avvicinamento a Ω ({T^t}) è importante in molti problemi.

L'assioma A di Smale è composto da due parti: 1) l'insieme Ω ({T^t}) è iperbolico, cioè consiste interamente di punti iperbolici; 2) i punti periodici sono densi in Ω ({T^t}). Smale ha dimostrato che per un SD che soddisfa all'assioma A l'insieme Ω ({T^t}) può essere rappresentato in maniera unica nella forma Ω ({T^t}) = ⋃ _i = ₁ Ω_i, dove ciascun Ω_i è chiuso e invariante, e la restrizione della dinamica a ciascun Ω_i è topologicamente transitiva (v. cap. 2). Smale ha chiamato ‛decomposizione spettrale' questa rappresentazione, e ‛sottoinsiemi fondamentali' i sottoinsiemi Ω_i.

Smale (v., 1970) ha inoltre proposto la seguente versione modificata della nozione di stabilità strutturale: il SD {T^t} è detto ‛Ω-strutturalmente stabile' se per ogni sistema perturbato, {T1^t}, abbastanza vicino (nella topologia C¹) le restrizioni dei SD ai loro Ω-insiemi sono topologicamente equivalenti.

Il principale scopo di Smale era dimostrare che, con alcune deboli assunzioni addizionali, l'assioma A era equivalente alla stabilità Ω-strutturale. Il fatto che l'assioma A discenda da questa stabilità è stato dimostrato molto presto da diversi autori (v., ad es., Smale 1967 e 1970); l'inverso si è rivelato assai più difficile ed è stato dimostrato soltanto circa venti anni dopo, nel 1988, da R. Mañé (v. Palis e Takens, 1993).

Una delle principali idee nuove della teoria dei sistemi che soddisfano all'assioma A era connessa con la scoperta di insiemi invarianti che non sono varietà, in quanto in alcune direzioni (solitamente stabili) essi hanno la struttura di un insieme di Cantor. Insiemi di questo tipo sono comunemente detti ‛frattali'. Ruelle e Takens (v., 1971), in un lavoro dedicato alla descrizione della turbolenza, hanno introdotto l'espressione ‛attrattore strano' per indicare un sottoinsieme invariante dello spazio delle fasi, con proprietà di attrattore pur non essendo una varietà e con dinamica complicata, ad esempio iperbolica. Finora non sono stati trovati nei SD attrattori strani che corrispondano all'equazione di Navier-Stokes, ma tale idea si è ampiamente diffusa in fisica, economia, biologia, ecc. In particolare, il sistema di Lorenz illustrato nel cap. 1 possiede, in un'ampia regione dello spazio dei parametri, degli attrattori strani molto interessanti; esso fu descritto per la prima volta da Lorenz in un articolo del 1963, e quindi ben prima della nascita della teoria di Smale, ma per lungo tempo non fu preso in considerazione dai matematici - principalmente perché apparso su una rivista non di matematica - ed ebbe ampia diffusione tra questi soltanto alla fine degli anni settanta. La struttura dell'attrattore nel sistema di Lorenz è stata studiata da molti matematici, fra i quali J. Guckenheimer, L. Williams, L. Shilnikov, V. Afraimovich, L. Bunimovich, Sinai e altri (v. Sinai, 1989).

Le diverse definizioni di attrattori strani sono state discusse in alcuni articoli (v., ad es., Milnor, 1985; v. Sinai, 1979). Si può collegare la presenza di attrattori strani nei sistemi di Hénon e simili studiati da Benedicks e Carleson (v., 1991) e da Viana e Mora con le biforcazioni di traiettorie omocline vicino al punto di tangenza di varietà stabili e instabili. Questo permette di dimostrare l'esistenza di attrattori strani in SD importanti, come ad esempio i sistemi di van der Pol o di Duffing nella teoria delle oscillazioni non lineari. Le dimostrazioni sono basate sul metodo detto ‛di Melnikov' (v. Arnold, 1989² e 1993), che permette, in alcuni casi, di studiare la separazione degli spazi tangenti in varietà stabili e instabili in funzione dei parametri nel membro di destra della (1).

d) Teoria delle biforcazioni.

Biforcazioni con raddoppio di periodo e universalità di Feigenbaum. - Circa vent'anni fa è stata fatta una notevole scoperta nella teoria dei sistemi dinamici connessa con l'accumulazione di biforcazioni che raddoppiano il periodo. Inizialmente sono state studiate alcune famiglie a un parametro di trasformazioni unidimensionali, come ad esempio la famiglia di trasformazioni quadratiche x → ax (1 - x) = T_a x, x ∈ [0, 1]. Era noto che in queste trasformazioni le orbite periodiche devono soddisfare alcune regole di coesistenza dette ‛ordine di Sharkovski' (v. Sharkovski, 1964; v. Sinai, 1994). Molti studi numerici hanno inoltre mostrato che spesso il variare del carattere della dinamica al variare del parametro passa attraverso una sequenza di biforcazioni che raddoppiano il periodo delle orbite. Questo significa che un'orbita periodica stabile che attrae orbite da quasi tutti i punti x vicini a essa diventa instabile e viene sostituita da un'altra orbita periodica stabile il cui periodo è due volte quello della precedente. Indichiamo con a_n il valore del parametro corrispondente a una biforcazione di questo tipo e supponiamo, per chiarezza, che a₁ 〈 a₂ 〈 ... 〈 a_n-1 〈 a_n 〈 .... Allora, per a leggermente più grande di a_n le mappe hanno un'orbita stabile periodica di periodo m₀ • 2ⁿ circondata da orbite instabili di periodo m₀ 2^k, k 〈 n. Feigenbaum (v., 1978 e 1979) ha mostrato che la successione a_n si comporta in maniera universale, nel senso che a_n converge a un limite a_∞ e a_n - a∞ ~ C λ^-n, dove C dipende dal SD in esame e λ = 4,6692... è la famosa ‛costante universale di Feigenbaum'. Il fatto notevole è che λ non dipende dallo spazio delle fasi e dal SD in esame.

La spiegazione di questo fatto data da Feigenbaum è basata sulle idee della teoria del gruppo di rinormalizzazione, teoria formulata nell'ambito della meccanica statistica. I teoremi matematici che sostengono la spiegazione di Feigenbaum sono stati dimostrati da Collet e Eckmann (v., 1980), da Lanford (v., 1982) e da altri. L'equazione funzionale principale è stata derivata anche da Coullet e Tresser (v., 1978) e da Derrida e altri (v., 1979; per i risultati più recenti v. de Melo e van Strien, 1993). Questa teoria può essere estesa a SD con tempo continuo e a spazi delle fasi multidimensionali. L'universalità di Feigenbaum è stata osservata in molti esperimenti concreti, ed è diventata molto famosa: la sua importanza deriva dal fatto che il limite della cascata di biforcazioni che raddoppiano il periodo è solitamente associato alla nascita di una dinamica fortemente caotica e di regimi di tipo turbolento.

Biforcazioni globali. - In molti casi è importante studiare i SD che dipendono da uno o più parametri e cambiano comportamento dinamico a seconda del valore di questi parametri. In questo modo nascono le tipiche biforcazioni nel carattere della dinamica, delle quali sono un esempio le biforcazioni che raddoppiano il periodo, discusse in precedenza. Le più studiate sono le biforcazioni locali connesse con il cambiamento della struttura della dinamica vicino a orbite fisse o periodiche. Talvolta esse sono responsabili della transizione tra regime stabile e regime instabile, e viceversa. Durante gli ultimi anni è stata dedicata molta attenzione alle biforcazioni globali nelle quali possono apparire nuovi insiemi invarianti, strati stocastici, ecc. Questa parte della teoria dei SD è connessa con la teoria delle catastrofi. Come esempio, possiamo ricordare le biforcazioni dette ‛omocline', che si trovano quando varietà stabili e instabili si intersecano in maniera non trasversale (per una dettagliata discussione di questi problemi, v. Palis e Takens, 1993). Un nuovo fenomeno robusto, consistente nell'apparire di SD con un numero infinito di attrattori (pozzi), è stato scoperto da S. Newhouse (v., 1974).

e) Metodi analitici.

Esiste un'ampia classe di sistemi dinamici in cui le variabili di fase possono essere decomposte in variabili ‛veloci' e variabili ‛lente'. Questo vuol dire che le equazioni del moto contengono un parametro piccolo e che la variazione delle variabili lente durante l'unità di tempo dipende da questo parametro e tende a zero quando questo parametro tende a zero. Il metodo naturale per studiare dei SD di questo tipo è quello che fa uso delle equazioni di prima approssimazione, in cui il valore delle variabili lente è fissato. A questo punto la dinamica delle variabili veloci può essere studiata in dettaglio, talvolta è addirittura integrabile. Fatto questo, si possono scrivere le equazioni per l'evoluzione delle variabili lente sostituendo nel membro di destra le medie temporali delle funzioni delle variabili veloci. In alcuni casi è possibile stimare la precisione di questa approssimazione e scrivere una teoria perturbativa che fornisca uno sviluppo in serie formale per la dinamica. Questa teoria ha molte applicazioni fisiche importanti (invarianti adiabatici, meccanica celeste, fisica dei plasmi, ecc.). (Per una descrizione dettagliata del metodo delle medie, v. Bogolyubov e Mitropolski, 1955; v. Arnold, 1993).

In molti problemi le proprietà della dinamica sono studiate con l'aiuto del tempo ‛complesso' e i potenti strumenti dell'analisi complessa, grazie ai quali si può descrivere la dinamica vicino a complicate singolarità non generiche. Uno dei risultati più straordinari in questo campo è la dimostrazione, da parte di Il′yashenko (v., 1991) e di Ecalle (v., 1992), del fatto che l'equazione

,

dove P e Q sono polinomi, ha un numero finito di cicli limite (problema detto ‛di Dulac').

4. Teoria ergodica dei sistemi dinamici

La teoria ergodica studia le proprietà statistiche della dinamica. Gli insiemi statistici sono specificati con l'aiuto della nozione di misura invariante. Sia μ una probabilità, cioè una misura normalizzata definita su una σ-algebra naturale di sottoinsiemi (eventi) di uno spazio delle fasi M dove agisce un SD {T^t}: μ è detta invariante sotto il sistema dinamico {T^t} se per ogni funzione misurabile e limitata f e ogni t ammissibile

Una formulazione equivalente della (4) dice: per ogni t ammissibile, μ {A} = μ {x ∣T^t x ∈ A} ^d=^ef μ {(T^t)^-1 A}, dove (T^t)^-1 A è l'intera controimmagine di A.

Il primo risultato importante nella teoria ergodica è il cosiddetto teorema ergodico di Birkhoff: per ogni funzione f per cui ∫ ∣f∣dμ 〈 ∞ esiste per quasi ogni x il limite

Se t ∈ z;¹ o r;¹ allora esistono gli analoghi limiti ô ^- (x) e ô ⁺ (x) = ô ^- (x) quasi ovunque. La media temporale ô ⁺ è invariante sotto la dinamica e ∫ fdμ = ∫ ô ⁺ dμ.

Esistono altri teoremi ergodici, come quello di von Neumann, quello di Hopf, quello di Wiener, il teorema ergodico subadditivo di Kingman (v. Walters, 1982; v. Sinai, 1989), come pure teoremi ergodici in cui il tempo è un gruppo multidimensionale, abeliano o non abeliano.

Il sistema dinamico {T^t} è detto ergodico se per quasi ogni x

cioè se le medie temporali coincidono con le medie spaziali. Poiché ogni SD con una misura invariante può essere decomposto in componenti ergodiche, dopo aver modificato il SD su di un sottoinsieme di misura nulla, si può definire una partizione ξ^(inv) di M tale che su ciascun elemento C_{ξ (inv)} si possa introdurre una ‛misura condizionale': ciascun C_{ξ (inv)} è invariante rispetto alla dinamica e il SD ristretto a ciascun C_{ξ (inv)} è ergodico.

Talvolta i SD che differiscono soltanto su sottoinsiemi di misura nulla sono detti uguali (mod 0). Adotteremo questa terminologia nel seguito.

Il SD {T^t} è detto mescolante se per ogni coppia di sottoinsiemi A ⊂ M, B ⊂ M e t → ∞

μ (A ⋂ T^t B) → μ (A) μ (B).

La nozione di ergodicità è stata introdotta da L. Boltzmann a proposito del problema generale dei fondamenti della fisica statistica; la nozione di sistema mescolante è stata introdotta da J. Gibbs. In seguito è diventato chiaro che il loro ruolo nella fisica statistica è molto più limitato di quanto ci si aspettasse. Comunque, vi è un gran numero di problemi legati all'ergodicità e al mescolamento di classi concrete di SD in spazi delle fasi a dimensione non molto grande nella dinamica non lineare, in fisica e in altre applicazioni della teoria dei SD.

Esistenza di misure invarianti. - In alcuni casi la forma delle equazioni del moto determina una misura invariante naturale. Nei sistemi hamiltoniani in cui l'hamiltoniana H non dipende esplicitamente dal tempo, la misura d μ = dpdq, detta ‛di Liouville', è invariante, e solitamente essa è infinita. Ma la restrizione della misura di Liouville a una qualsiasi varietà a energia costante H = cost induce una misura invariante che spesso può essere normalizzata. Nella meccanica statistica questa è detta ‛distribuzione microcanonica'.

Talvolta si può dimostrare l'esistenza di almeno una misura invariante nei SD con spazio delle fasi compatto, usando il metodo detto di Bogolyubov-Krylov (v. Cornfeld e altri, 1982; v. Sinai, 1989). Se un SD possiede soltanto una misura invariante, esso è ergodico rispetto a questa misura ed è detto ‛fortemente ergodico'. Nei SD con comportamento iperbolico, solitamente ci sono molte misure invarianti; tuttavia sono stati elaborati diversi metodi che permettono di ottenere delle misure naturali invarianti che sono, in un certo senso, costruite dalla dinamica stessa. A questo riguardo, particolare attenzione è stata dedicata alle trasformazioni unidimensionali: Jakobson (v., 1981) ha dimostrato ad esempio che, per la famiglia di trasformazioni quadratiche T_a : x → ax (1 - x), 0 〈 a ≤ 4, l'insieme di valori di a per cui T_a possiede una misura invariante assolutamente continua ha misura di Lebesgue positiva. Una simile dimostrazione per le trasformazioni di Hénon è stata fornita da Benedicks e Carleson (v., 1991), e in seguito essa è stata estesa da Mora e Viana a classi di trasformazioni più generali (v. Palis e Takens, 1993).

Spettro di un SD. - Supponiamo che t ∈ Z¹ o R¹. Per ogni f, g ∈ L² (M, μ) consideriamo

Queste sono dette correlazioni temporali o, più semplicemente, funzioni di correlazione e sono rilevanti in molti problemi di dinamica non lineare e di meccanica statistica di non equilibrio, in particolare in relazione con la definizione dei coefficienti di trasporto e delle formule dette di Green-Kubo. Per f = g si può scrivere:

dove σ è una misura finita. Essa è detta misura spettrale di f.

Un concetto strettamente legato è quello del gruppo degli operatori unitari {U^t} che agiscono su L² (M, μ) in base alla relazione (U^t f) (x) = f (T^t x). Tutte le proprietà dei SD che possono essere espresse in termini del gruppo {U^t} sono dette proprietà spettrali: l'ergodicità e il mescolamento ne costituiscono degli esempi.

Isomorfismi metrici di SD e invarianti metrici. - Supponiamo di avere un SD {T1^t} che agisce sullo spazio delle fasi M₁ con misura invariante μ₁, e un altro SD {T2^t} che agisce sullo spazio delle fasi M₂ con misura invariante μ₂. I sistemi dinamici {T1^t} e {T2^t} sono detti ‛metricamente isomorfi' se esiste un isomorfismo (mod 0) ϕ che trasforma un sottoinsieme invariante M′₁ ⊂ M¹ di misura pari alla misura di M₁ in un sottoinsieme invariante M′₂ ⊂ M₂ di misura pari alla misura di M₂ che commuta con la dinamica, cioè tale che ϕT1^t = T2^t ϕ. Questa nozione permette di confrontare SD che agiscono su spazi delle fasi diversi: ϕ è una sorta di ‛cambio di variabili', che nella teoria ergodica può essere non differenziabile ma deve essere misurabile. In particolare, possono essere isomorfi anche SD che agiscono su spazi delle fasi a dimensione diversa. Le proprietà e le caratteristiche dei SD che sono condivise da tutti i SD metricamente isomorfi - per esempio, l'ergodicità, il mescolamento, il gruppo {U^t} - sono dette ‛invarianti metrici'.

Uno dei problemi più famosi nella teoria ergodica astratta è il problema degli isomorfismi metrici che consiste nel determinare un insieme completo di invarianti metrici tale da garantire che due sistemi siano o no metricamente isomorfi. Questo problema è stato oggetto di molti studi per lungo tempo; tuttavia, è ormai diventato chiaro che non esiste una risposta soddisfacente in un contesto completamente generale.

Sistemi dinamici con spettro puramente puntiforme. - Un SD ergodico è detto con spettro puramente puntiforme se il gruppo associato {U^t} possiede una base completa di autofunzioni. Questa nozione e la teoria di tali SD sono state elaborate da J. von Neumann (v., 1932). I principali risultati possono essere riassunti come segue: 1) lo spettro di ciascun SD ergodico con spettro puramente puntiforme è un gruppo abeliano; 2) il valore assoluto di ciascuna autofunzione è costante quasi ovunque; 3) lo spettro costituisce un insieme completo di invarianti metrici, cioè due SD ergodici con spettro puramente puntuale sono metricamente isomorfi se e solo se essi hanno lo stesso spettro. In tali sistemi - solamente ergodici e non mescolanti - le funzioni di correlazione temporali sono funzioni quasi periodiche del tempo. Un tipico esempio è il flusso sul toro n-dimensionale:

Nell'interpretazione naturale, ϕ_i sono delle fasi e ω_i le frequenze corrispondenti, non commensurabili.

Nei sistemi hamiltoniani integrabili le restrizioni della dinamica ai tori invarianti generano dei SD con spettro puramente puntuale. La teoria KAM mostra la persistenza di questo tipo di dinamica sotto piccole perturbazioni della hamiltoniana. Infatti, come ricordato sopra (v. cap. 3, § a), il risultato principale della teoria KAM dice che le piccole perturbazioni dei SD integrabili hanno un insieme di misura finita costituito da tori invarianti. La restrizione della dinamica a ciascuno di questi tori genera dei SD con spettro puramente puntuale che hanno, in qualche sistema di coordinate, la forma (5).

Entropia. - L'entropia di un SD è un altro invariante metrico importante per alcune classi di SD con spettro continuo. Supponiamo che t ∈ z;¹. Consideriamo una partizione finita η di M in sottoinsiemi C₁, C₂, ..., C_r. La sua entropia è:

Indichiamo con ηn_m la partizione i cui elementi sono ⋂_m≤k≤n T^k C_ik. Si verifica facilmente che esiste sempre h (T, η) = lim_n → ∞

h (ηn₀).

Si definisce h (T) = sup_η h (T, η) ‛entropia' del SD {T^t}. Nel caso di tempo continuo si può dimostrare che h (T^-t) = h (T^t), e che h (T^t) è una funzione lineare di t, cioè che h (T^t) = ∣t∣h (T¹). Quindi si può sempre porre h (T^t) = h (T¹).

La nozione di entropia è apparsa per la prima volta in un articolo di Kolmogorov (v., 1958). In seguito, la sua definizione è stata modificata e ha preso la forma presentata sopra. Attualmente la teoria dell'entropia è una delle parti più affascinanti e sviluppate della teoria ergodica (v. Cornfeld e altri, 1982; v. Ornstein, 1974; v. Sinai, 1989 e 1994; v. Walters, 1982).

L'entropia dei SD con spettro puramente puntuale è nulla. Le traslazioni di Bernoulli e quelle di Markov (v. cap. 1) hanno entropia positiva; i processi stocastici gaussiani hanno in molti casi entropia infinita.

Sistemi K. Problema degli isomorfismi per sistemi K. - Nell'articolo di Kolmogorov (v., 1958), citato in precedenza, fu proposta un'altra nozione importante: quella di sistema K. Un SD {T^t} è detto sistema K se esiste una partizione misurabile ζ⁽⁰⁾ tale che: 1) T^t ζ⁽⁰⁾ = ζ^(t) ≥ ζ⁽⁰⁾ per t > 0; 2)

ζ^(t) = ε, dove ε è la partizione in punti; 3)

ζ^(t) = ν, dove ν è la partizione banale contenente il solo elemento M.

Questa definizione è stata motivata da nozioni simili presenti nella teoria dei processi stocastici. In quel caso il ruolo delle partizioni ζ^(t) è svolto dalle ‛code' della realizzazione del processo stocastico, da - ∞ fino a t.

In questa forma la definizione di sistema K è piuttosto astratta. Se ne può dare una formulazione equivalente in termini delle σ-subalgebre che la rende più chiara a quanti abbiano familiarità con analoghe nozioni di teoria della probabilità. In effetti, la proprietà espressa nella definizione precedente implica, in un certo senso, una perdita di memoria nel corso della dinamica. Il suo ruolo nelle applicazioni della teoria ergodica è dovuto al fatto che in molti casi è più facile dimostrare che un SD è un sistema K che non ricavarne direttamente le altre proprietà che ne seguono.

I sistemi K sono ergodici, mescolanti, hanno spettro continuo ed entropia positiva. Kolmogorov pensava che l'entropia potesse rappresentare l'insieme completo di invarianti metrici all'interno della classe dei sistemi K, ma si è poi verificato che questo è falso. Ornstein (v., 1974) ha sviluppato una nuova tecnica che permette di dimostrare che l'entropia è un invariante completo per le traslazioni di Bernoulli, e ha anche trovato un metodo interessante per dimostrare l'isomorfismo di molti generi di SD con le traslazioni di Bernoulli. Vi sono peraltro dei sistemi K che non sono isomorfi alle traslazioni di Bernoulli, e anche tra di essi esiste un'infinità non numerabile di classi di sistemi K non isomorfi. Da un punto di vista generale, il problema dell'isomorfismo per i sistemi di Bernoulli è un problema di costruzione di codici speciali, detti ‛codici stazionari'. La tecnica sviluppata per il problema dell'isomorfismo delle traslazioni di Bernoulli si è poi rivelata utile anche nell'ambito della teoria dell'informazione.

Esponenti di Lyapunov, teorema ergodico moltiplicativo di Oseledetz e teoria di Pesin. - La teoria dell'entropia è strettamente connessa con la teoria dei SD con comportamento iperbolico. Il primo passo in questo senso è basato sul cosiddetto teorema ergodico moltiplicativo di Oseledetz (v., 1968; v. Sinai, 1989; v. Katok, 1980). Esso è solitamente formulato per SD differenziabili che agiscono su varietà differenziabili dotate di una misura invariante μ.

Consideriamo un punto x e lo spazio tangente T_x. Supponiamo per semplicità che il SD sia ergodico. Il teorema afferma che esistono dei numeri λ₁ > λ₂ > ... > λ_k, k ≤ dim n, detti esponenti di Lyapunov, e per μ-quasi ogni punto x il filtro T_x = Tx⁽¹⁾ ⊃ Txx⁽²⁾ ⊃ ... ⊃ Tx^(k), dove Tx⁽ⁱ⁾ sono sottospazi di T_x tali che: 1) dT^t Tx⁽ⁱ⁾ = T ($¹_T)_tx ; 2) per ogni e ∈ Tx⁽ⁱ⁾ - Tx⁽ⁱ⁺¹⁾ esiste il limite

Si ricordi che dTx^t è la trasformazione di Jacobi che trasforma lo spazio tangente T_x nello spazio tangente T_T^tx (in coordinate locali essa è data dalla matrice delle derivate prime). Questo teorema mostra che per punti x tipici le soluzioni delle equazioni di Jacobi crescono esponenzialmente e che gli esponenti sono gli esponenti di Lyapunov, μ-quasi ovunque uguali.

Il passo successivo è stato compiuto da Pesin (v., 1977), il quale ha mostrato che le famiglie {T_x⁽ⁱ)} sono integrabili, nel senso che esistono varietà locali, stabili o instabili, tali che per ciascuna di esse la convergenza esponenziale ha luogo con velocità determinata dagli esponenti di Lyapunov.

Katok (v., 1980) ha dimostrato che per SD ergodici l'entropia h ≤ Σ⁺ λ_i (dim Tx⁽ⁱ⁾ - dim Tx^(i-1)). Qui Σ⁺ indica la somma sugli esponenti di Lyapunov positivi. L'uguaglianza non è sempre verificata.

La positività di almeno un esponente di Lyapunov è considerata una manifestazione di comportamento caotico. Inoltre risulta relativamente facile, da un punto di vista numerico, determinare i più grandi esponenti di Lyapunov, anche se solitamente tale determinazione non è sufficiente per una dimostrazione matematica. Nondimeno, chi si occupa di applicazioni di questa teoria parla di caos quando ha motivo di ritenere che esistano degli esponenti di Lyapunov positivi.

Misure BRS. - In sistemi con comportamento iperbolico esistono delle misure invarianti speciali, che sono in un certo senso le più naturali. Esse sono state costruite per la prima volta per sistemi di Anosov (v. Sinai, 1972) e in seguito per sistemi soddisfacenti l'assioma A (v. Bowen, 1975; v. Bowen e Ruelle, 1975; v. Ruelle, 1976).

Supponiamo che un SD soddisfacente l'assioma A {T^t} possieda un insieme fondamentale Ω che è un attrattore. In particolare, supponiamo che esso sia un sistema di Anosov. Consideriamo una misura arbitraria ν₀, assolutamente continua e concentrata in un piccolo intorno di Ω. La dinamica genera una famiglia di misure ν_t, dove ν_t (C) = ν₀ ((T^t)^-1 C). Sia μ_t =

ν_s ds. Qualunque punto limite della famiglia {μ_t} è concentrato nell'attrattore Ω. Nei sistemi assioma A e in altri sistemi con comportamento iperbolico esiste il limite debole μ = lim_t → ∞ μ_t, che non dipende da ν₀. In questi casi, μ è la misura naturale che determina le proprietà statistiche delle traiettorie intorno a Ω. Essa è detta misura BRS (Bowen-Ruelle-Sinai) e può essere caratterizzata a partire dalle sue proprietà intrinseche. La descrizione della misura BRS data sopra è dovuta a Ruelle (v., 1976). Relativamente ai SD hamiltoniani iperbolici, il principale problema consiste nel mostrare che μ è la distribuzione microcanonica. Nei sistemi dissipativi l'esistenza di μ è un problema difficile, che può essere risolto soltanto usando molte informazioni sulla dinamica stessa.

Il metodo usato per studiare la dinamica dei SD con comportamento iperbolico e le misure BRS sfrutta in diversi punti il legame con la fisica statistica d'equilibrio su reticolo. Per questo motivo esso è detto ‛formalismo termodinamico' (v. Ruelle, 1976). L'idea fondamentale è di costruire delle partizioni speciali dello spazio delle fasi, delle partizioni di Markov (v., ad. es., Sinai, 1972 e 1989) e di usarle per codificare le traiettorie dei SD in configurazioni di qualche modello di spin. In molti casi, la soggiacente misura invariante può essere riscritta come misura di Gibbs rispetto a una qualche lagrangiana. Questo metodo, quando può essere applicato, permette di approssimare il SD deterministico con una catena di Markov, di stimare il decadimento delle funzioni di correlazione temporali e di dimostrare che la distribuzione delle fluttuazioni delle medie temporali ha un limite gaussiano.

Tra i SD che sono stati studiati con l'aiuto di un formalismo termodinamico vi sono, in primo luogo, i sistemi di Anosov, e in particolare i flussi geodetici su varietà a curvatura negativa, il gruppo degli automorfismi di un toro e le loro perturbazioni. Ricordiamo anche alcuni tipi di biliardi, detti ‛biliardi iperbolici' (v. Sinai, 1991); tra di essi ci sono i biliardi in dominî dal contorno concavo. Ha destato una grande sorpresa, circa venti anni fa, la dimostrazione da parte di Bunimovich (v., 1974) del fatto che il biliardo all'interno di uno ‛stadio' è iperbolico ed ergodico. Questo tipo di biliardo è ben noto nella teoria del caos quantistico. È infine giusto menzionare i sistemi che soddisfano l'assioma A, cioè il sistema di Lorenz e alcune sue varianti, la trasformazione di Hénon e alcuni tipi di trasformazioni unidimensionali.

In base a un'ipotesi generale, lo spazio delle fasi di un SD generico consiste essenzialmente di tori con moto quasi periodico e di un sottoinsieme invariante con dinamica instabile iperbolica ed esponenti di Lyapunov positivi. Le informazioni disponibili confermano questa ipotesi nel caso di SD hamiltoniani, ma al momento non sembra possibile dimostrarla.

BIBLIOGRAFIA

Adler, R., Conheim, A., McAndrew, M., Topological entropy, in ‟Transactions of the American Mathematical Society", 1965, CXIV, pp. 309-319.

Andronov, A. A., Pontryagin, L. S., Systèmes grossiers, in ‟Doklady Akademii Nauk SSSR", 1937, XIV, pp. 247-251.

Anosov, D. V., Geodesic flows on closed Riemann manifolds with negative curvature, Providence, R. I., 1969.

Arnold, V. I., Small denominators and stability problems in classical and celestial mechanics, in ‟Russian mathematical surveys", 1963, XVIII, pp. 91-192.

Arnold, V. I., Instability of dynamical systems with many degrees of freedom, in ‟Doklady Akademii Nauk SSSR", 1964, CLVI, pp. 9-12.

Arnold, V. I., Mathematical methods of classical mechanics, New York 1989² (tr. it.: Metodi matematici nella meccanica classica, Roma 1992).

Arnold, V. I. (a cura di), Mathematical aspects of classical and celestial mechanics, Berlin-New York 1993.

Aubry, S., The twist map, the extended Frenkel-Kontorova model and the devil's staircase, in ‟Physica D: nonlinear phenomena", 1983, VII, pp. 240-258.

Benedicks, M., Carleson, L., The dynamics of the Hénon map, in ‟Annals of mathematics", 1991, CXXXIII, pp. 73-169.

Bogolyubov, N. N., Mitropolski, Yu. A., Asimptoticheskie metody v teorii nelineinykh Kolebanii, Moskva 1955 (tr. ingl.: Asymptotical methods in the theory of non-linear oscillations, Moscow 1974).

Bowen, R., Equilibrium states and the ergodic theory of Anosov diffeomorphisms, Berlin 1975.

Bowen, R., Ruelle, D., The ergodic theory of axiom A flows, in ‟Inventiones mathematicae", 1975, XXIX, pp. 333-339.

Bunimovich, L., Ergodic properties of some billiards, in ‟Functional analysis and its applications", 1974, VIII, pp. 73-74.

Chirikov, B. V., A universal instability of many-dimensional oscillator systems, in ‟Physics reports", 1979, LII, 5, pp. 263-379.

Coddington, E. A., Levinson, N., Theory of ordinary differential equations, New York 1955.

Collet, P., Eckmann, J.-P., Iterated maps on the interval as dynamical systems, Basel 1980.

Cornfeld, I. P., Fomin, S. V., Sinai, Ya. G., Ergodic theory, New York 1982.

Coullet, P., Tresser, C., Itérations d'endomorphismes et groupe de rénormalisation, in ‟Comptes rendus de l'Académie des Sciences de Paris", 1978, CCLXXXVII, pp. 577-580.

Derrida, B., Gervois, A., Pomeau, Y., Universal metric properties of bifurcations of endomorphisms, in ‟Journal of physics A: mathematical and general", 1979, XII, pp. 269-296.

Ecalle, J., Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac, Paris 1992.

Fatou, P., Sur les équations fonctionnelles, in ‟Bulletin de la Société Mathématique de France", 1919, XLVII, pp. 161-271 e 1920, XLVIII, pp. 33-94.

Feigenbaum, M., Qualitative universality for a class of non-linear transformations, in ‟Journal of statistical physics", 1978, XIX, pp. 25-52.

Feigenbaum, M., The universal metric properties of non-linear transformations, in ‟Journal of statistical physics", 1979, XXI, pp. 669-709.

Furstenberg, H., Recurrence in ergodic theory and combinatorial number theory, Princeton, N. J., 1981.

Hénon, M., A two-dimensional mapping with a strange attractor, in ‟Communications in mathematical physics", 1976, L, pp. 69-77.

Herman, M. R., Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations, in ‟Publications mathématiques de l'Institut des Hautes Études Scientifiques", 1979, XLIX, pp. 5-233.

Hirsch, M. W., Pugh, C. C., Shub, M., Invariant manifolds, Berlin-New York 1977.

Il'yashenko, Yu. S., Finiteness theorems for limit cycles, Providence, R. I., 1991.

Jakobson, M. V., Absolutely continuous invariant measures for one-parameter families of one-dimensional maps, in ‟Communications in mathematical physics", 1981, LXXXI, pp. 39-88.

Julia, G., Mémoire sur l'itération des fonctions rationnelles, in ‟Journal de mathématique", 1918, I, pp. 47-245.

Katok, A., Lyapunov exponents, entropy and periodic orbits for diffeomorphisms, in ‟Publications mathématiques de l'Institut des Hautes Études Scientifiques", 1980, LI, pp. 137-173.

Kolmogorov, A. N., General theory of dynamical systems and classical mechanics, in Proceedings of the International mathematical congress, 1954, vol. I, Amsterdam 1957, pp. 315-333.

Kolmogorov, A. N., New metric invariant of transitive dynamical systems and endomorphisms of Lebesgue spaces, in ‟Doklady Akademii Nauk SSSR", 1958, CXIX, pp. 861-884.

Lanford, O., A computer-assisted proof of the Feigenbaum conjectures, in ‟Bulletin of the American Mathematical Society", 1982, VI, pp. 427-434.

Lichtenberg, A. J., Lieberman, M. A., Regular and stochastic motion, New York 1983.

Lorenz, E., Deterministic non-periodic flow, in ‟Journal of the atmospheric sciences", 1963, XX, pp. 130-141.

Mather, J., Existence of quasi-periodic orbits for twist homeomorphisms of the annulus, in ‟Topology", 1982, XXI, pp. 457-567.

Melo, W. de, Strien, S. van, One-dimensional dynamics, Berlin-New York 1993.

Milnor, J., On the concept of attractor, in ‟Communications in mathematical physics", 1985, XCIX, pp. 177-195.

Moser, J., Lectures on Hamiltonian systems, Memoirs of the American Mathematical Society n. 81, Providence, R. I., 1968.

Neumann, J. von, Zur Operatorenmethode in der klassischen Mechanik, in ‟Annals of mathematics", 1932, XXXIII, pp. 587-642.

Newhouse, S., Diffeomorphisms with infinitely many sinks, in ‟Topology", 1974, XIII, pp. 9-18.

Olver, P. J., Sattinger, D. H. (a cura di), Solitons in physics, mathematics and non-linear optics, New York 1990.

Ornstein, D., Ergodic theory, randomness, and dynamical systems, New Haven, Conn.-London 1974.

Oseledetz, V., A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems, in ‟Proceedings of the Moscow Mathematical Society", 1968, XIX, pp. 197-231.

Palis, J., Takens, F., Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations, Cambridge-New York 1993.

Peixoto, M. M., Structure stability on two-manifolds, in ‟Topology", 1962, I, pp. 101-120.

Pesin, Ya. B., Characteristic Lyapunov exponents and smooth ergodic theory, in ‟Russian mathematical surveys", 1977, XXXII, pp. 55-114.

Ruelle, D., A measure associated with axiom A attractors, in ‟American journal of mathematics", 1976, XCVIII, pp. 619-654.

Ruelle, D., Thermodynamic formalism: the mathematical structures of classical equilibrium statistical mechanics, Reading, Mass., 1978.

Ruelle, D., Takens, F., On the nature of turbulence, in ‟Communications in mathematical physics", 1971, XX, pp. 167-192.

Sharkovski, A., Coexistence of cycles of a continuous map of the line into itself, in ‟Ukrainian mathematical journal", 1964, XVI, pp. 61-71.

Shilnikov, L., Existence of a countable set of periodic motions in four-dimensional space in an extended neighborhood of a saddle-focus point, in ‟Doklady Akademii Nauk SSSR", 1967, CLXXII, pp. 54-57.

Sinai, Ya. G., Gibbs measures in ergodic theory, in ‟Russian mathematical surveys", 1972, XXVII, 4, pp. 21-69.

Sinai, Ya. G., Stochasticity of dynamical systems, in Proceedings of the winter school ‟Non-linear waves", Moscow 1979, pp. 192-212.

Sinai, Ya. G. (a cura di), Ergodic theory with applications to dynamical systems and statistical mechanics, New York 1989.

Sinai, Ya. G., Hyperbolic billiards, in Proceedings of the International congress of mathematicians in Kyoto, vol. I, New York 1991, pp. 249-260.

Sinai, Ya. G., Topics in ergodic theory, Princeton, N. J., 1994.

Smale, S., Diffeomorphisms with many periodic points, in Differential and combinatorial topology (a cura di S. S. Cairns), Princeton, N. J., 1965, pp. 63-80.

Smale, S., Differentiable dynamical systems, in ‟Bulletin of the American Mathematical Society", 1967, LXXIII, pp. 747-817.

Smale, S., The Q-stability theorem, in Proceedings of the 14th Symposium in pure mathematics of the American Mathematical Society, Providence, R. I., 1970, pp. 289-297.

Walters, P., An introduction to ergodic theory, New York 1982.

Weyl, H., Über die Gleichverteilung von Zahlen mod Eins, in ‟Mathematische Annalen", 1916, LXXVII, pp. 313-352.

Zaslavski, G. M., Sagdeev, R. Z., Usikov, D. A., Chernikov, A. A., Weak chaos and quasi-regular patterns, Cambridge-New York 1991.