Sistemi reagenti complessi
Sistemi reagenti complessi
Le scienze chimiche devono spesso fronteggiare problemi concernenti l'analisi e la descrizione di sistemi nei quali sono presenti molti componenti che interagiscono fra di loro in un insieme di reazioni reciprocamente interconnesse. Inoltre possono essere presenti effetti di retroazione in virtù dei quali in una sequenza di reazioni successive la velocità di formazione di alcuni componenti viene influenzata da specie prodotte a valle della sequenza stessa. Ulteriori fattori di complessità sono la presenza di espressioni non lineari delle velocità con le quali si svolgono le reazioni e l'intervento di processi diffusivi dei diversi componenti. Dalla combinazione dei fenomeni precedenti possono emergere comportamenti inaspettati, con formazione di configurazioni spaziali non omogenee delle concentrazioni dei componenti che si propagano e oscillano nel tempo. Situazioni di questa natura sono comuni: si riscontrano nella catalisi, nella chimica colloidale, nella sintesi dei materiali, nella biochimica e così via. Secondo J. Watson (2003), la vita non è che una vastissima gamma di reazioni chimiche coordinate. Questa autorevole affermazione sembra legittimare gli sforzi che vengono condotti per costruire modelli atti alla descrizione del comportamento delle cellule, fruendo delle conoscenze sul modo nel quale le molecole reagiscono e si diffondono.
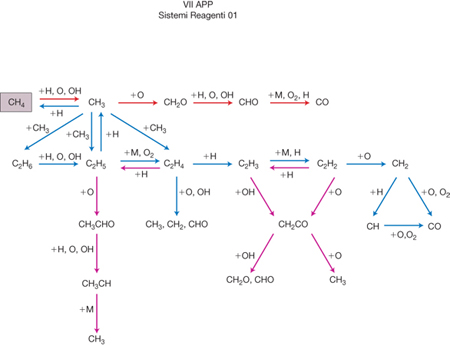
Quale primo esempio di s. r. c. si possono menzionare i processi di combustione nei quali gli idrocarburi si combinano con l'ossigeno a temperature superiori ai 1000 °C, portando alla formazione finale di anidride carbonica e acqua con liberazione di quantità significative di energia. In realtà tali trasformazioni si svolgono attraverso decine di reazioni che coinvolgono molte specie intermedie, come viene illustrato nella fig. 1 relativa all'ossidazione del metano. Anche l'energia utilizzata dagli organismi viventi viene prodotta attraverso reazioni di combustione nelle quali gli idrati di carbonio vengono trasformati in anidride carbonica e acqua attraverso uno schema complesso di reazioni, detto ciclo di Krebs, che si svolge però in soluzione e a temperatura ordinaria.
L'oggetto della cinetica chimica è la descrizione dell'evoluzione nel tempo dei sistemi menzionati; per perseguire questo scopo è necessario anzitutto individuare un insieme di reazioni che caratterizzano la formazione e la scomparsa delle diverse specie coinvolte. Tale obiettivo può essere perseguito sperimentalmente fruendo di metodi analitici sempre più sofisticati che permettono di evidenziare quantitativamente anche piccole quantità di composti intermedi. Nel prosieguo le reazioni verranno contrassegnate con la lettera k, mentre i diversi componenti verranno indicati con Ai, per cui ciascuna di esse verrà concisamente scritta come segue:
✄
dove υik è il coefficiente stechiometrico del componente i nella k-sima reazione, N il numero dei componenti e M quello delle reazioni. Ovviamente, poiché solo pochi dei componenti presenti nel sistema prendono parte a ciascuna reazione, molti υik sono uguali a zero. Ciascuna reazione è caratterizzata da una velocità rk che esprime il numero di moli di un componente di riferimento che si trasforma per unità di tempo e di volume. Essa dipende dalla temperatura e dalle concentrazioni dei reagenti attraverso espressioni matematiche il più delle volte non lineari su cui si ritornerà in seguito.
Se si definisce una zona dello spazio nella quale si svolge la trasformazione in esame, e per semplicità si assume che al suo interno non siano presenti variazioni di concentrazione dei componenti, cioè che il sistema sia ben rimescolato, ne deriva che il bilancio di ciascuna specie si può esprimere come segue:
✄
dove t è il tempo e Ci la concentrazione molare del componente i, Cj indica l'insieme delle concentrazioni presenti nella miscela reagente e infine ϕil il flusso del componente i entrante o uscente con la corrente l nella zona di reazione dall'esterno.
Il precedente costituisce un sistema di equazioni differenziali ordinarie, una per ciascun componente, non lineari soprattutto per la forma dell'espressione della velocità di reazione. La sua soluzione, per lo più perseguibile per via numerica, permette di ottenere la variazione delle diverse concentrazioni nel tempo e quindi l'evoluzione del sistema reagente. Se esso è aperto agli scambi di materia con l'esterno, e quindi i valori dei flussi ϕil sono diversi da zero, si può raggiungere una condizione stazionaria in corrispondenza della quale le concentrazioni si mantengono inalterate nel tempo. In questo caso le loro derivate rispetto al tempo, presenti al primo membro, sono tutte nulle e il calcolo dei loro valori viene perseguito risolvendo un sistema di equazioni algebriche del tipo:
✄
Trattandosi di un sistema non lineare si possono presentare diverse soluzioni corrispondenti a una molteplicità di stati stazionari, ciascuno caratterizzato dai valori Csi delle concentrazioni, il cui numero e le cui caratteristiche dipendono anche dai valori specifici dei flussi ϕil che acquistano così il ruolo di parametri di controllo del sistema. Essi possono essere rispettivamente stabili o instabili, a seconda del comportamento che il sistema manifesta se viene assoggettato a una fluttuazione delle concentrazioni. Infatti esso risulta stabile se tende a recuperare in modo autonomo lo stato iniziale e instabile se si evolve verso un altro stato. L'analisi di stabilità viene perseguita linearizzando le equazioni differenziali mediante uno sviluppo in serie troncato al primo termine dei secondi membri. È opportuno riferire inoltre le concentrazioni dai loro corrispondenti scostamenti dai valori degli stati stazionari, scrivendo ciascuna equazione nella forma:
✄
dove ΔCi=Ci−Csi indica prorio la differenza fra la concentrazione attuale e la concentrazione del suo corrispondente stato stazionario. La soluzione della precedente equazione differenziale lineare ha la seguente forma:
✄
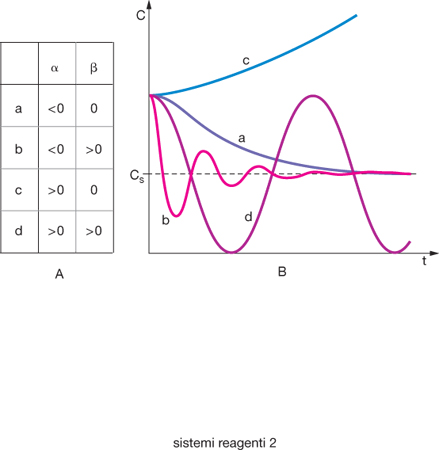
I valori dei parametri Bj vengono valutati dalle condizioni iniziali mentre gli esponenti σ, denominati di Liapunov, sono gli autovalori della matrice dei coefficienti delle corrispondenti equazioni linearizzate, e sono dei numeri complessi del tipo σ=α+iβ. Come illustrato nella fig. 2, a seconda dei valori assunti dai parametri α e β, si presenta una variata tipologia di situazioni che corrispondono rispettivamente a stati stabili (nei quali ΔCi tende a zero e il sistema che ha subito una perturbazione recupera la configurazione iniziale), instabili (nei quali in seguito a una perturbazione il sistema si allontana dallo stato stazionario iniziale) o oscillanti (nei quali le concentrazioni variano periodicamente nel tempo). Un esempio tipico e largamente menzionato di reazione oscillante è quella di Belousov-Zhabotinsky, che si realizza mescolando un bromato alcalino, un sale di cerio e acido maleico; se si opera in un reattore ben agitato si osserva una tipica variazione periodica della colorazione della soluzione cha passa dal blu al rosso.
Infine, è importante menzionare che l'analisi di stabilità dinamica, oltre a caratterizzare il comportamento di sistemi chimici, ha anche importanti ricadute sia nel controllo di sistemi di interesse applicativo, quali i grandi reattori industriali e i processi di combustione, sia per formulare lo sviluppo di strategie per la sintesi di composti chimici e di materiali.
La velocità delle singole reazioni
Protagonista delle trasformazioni che hanno luogo nei sistemi reagenti è la velocità r con la quale si svolgono le singole reazioni, espressa come moli di un componente di riferimento che si trasforma per unità di tempo e unità di volume del sistema stesso. In generale essa dipende dalle variabili di stato (T, temperatura; p, pressione) e dalle concentrazioni Ci delle diverse specie presenti nel sistema.
In generale si scrive: r=k(T) f(concentrazione dei reagenti) dove k, che viene detta costante di velocità di reazione, dipende dalla temperatura secondo l'espressione ✄, in cui E# è una energia detta di attivazione e R la costante dei gas.
In fase gassosa la velocità dipende dalla frequenza delle collisioni fra le molecole, la quale è proporzionale al prodotto delle loro concentrazioni. Su scala molecolare la reazione chimica avviene attraverso la rottura e la formazione di legami fra gli atomi che sono presenti rispettivamente nei reagenti e nei prodotti di reazione. La trasformazione può essere descritta mediante una tipica superficie, definita potential energy surface (PES), che fornisce l'energia potenziale del sistema in funzione delle distanze fra gli atomi direttamente coinvolti e su cui si può seguire il percorso del passaggio dai prodotti ai reagenti, chiamato cammino di reazione. La dinamica della collisione può essere studiata descrivendo il moto del punto che rappresenta il sistema molecolare reagente sulla PES. Affinché la reazione abbia luogo è necessario che venga superata la barriera di energia potenziale E# e perché ciò si verifichi è necessario che l'energia delle molecole reagenti sia sufficientemente elevata. Alternativamente il calcolo può essere affrontato mediante la termodinamica statistica, tenendo conto che il flusso medio dei reagenti che attraversa una particolare zona della PES alla sommità della barriera porta ai prodotti di reazione.
In questa impostazione si ricava che la costante k è espressa da ✄, dove kB è la costante di Boltzmann e h quella di Planck, mentre ΔG# è la variazione di energia libera relativa al passaggio dai reagenti allo stato di transizione: il complesso molecolare instabile che si trova alla sommità della barriere di energia potenziale. Malgrado la sua esistenza sia effimera, poiché ha una vita media di 10−12÷10−11s, dall'andamento della PES alla sommità della barriera si possono calcolare le sue caratteristiche geometriche e le frequenze di vibrazione degli atomi, indispensabili per calcolare la ΔG#. Grazie alle conoscenze accumulate nel settore della spettroscopia molecolare e ai progressi raggiunti in quello della chimica computazionale, è possibile valutare con ragionevole accuratezza i dati necessari per calcolare con la relazione precedente la costante di velocità di reazione.
Sebbene originariamente concepita per reazioni in fase gassosa, la teoria dello stato di transizione è stata applicata con successo anche alle reazioni che hanno luogo in fase liquida. In un'analisi approfondita, H.A. Kramers e H.C. Brinkman hanno assimilato una reazione in fase condensata alla fuoriuscita di una particella da una buca di potenziale, che talora costituisce una vera e propria gabbia di solvente, in conseguenza dell'energia del moto termico casuale che gli viene conferita dall'ambiente circostante.
Se si considerano tre punti lungo una coordinata di reazione x, A e B, che sono corrispondenti rispettivamente ai minimi dell'energia potenziale dei reagenti e dei prodotti, e C, posto alla sommità della barriera di energia potenziale, è possibile dimostrare che la costante di velocità di reazione risulta espressa dalla formula seguente:
✄
dove μ è la viscosità del fluido, υ è la frequenza di vibrazione, supposta armonica, della particella nel punto A, m la sua massa e V(x) l'energia potenziale; k risulta inversamente proporzionale alla viscosità, che costituisce il parametro di accoppiamento con il sistema. Ciò accade poiché la velocità della reazione chimica è rallentata dalla diffusione in un liquido, a sua volta inversamente proporzionale alla viscosità. Si può dimostrare che quando essa assume valori bassi in senso relativo, si ricade nella teoria dello stato di transizione.
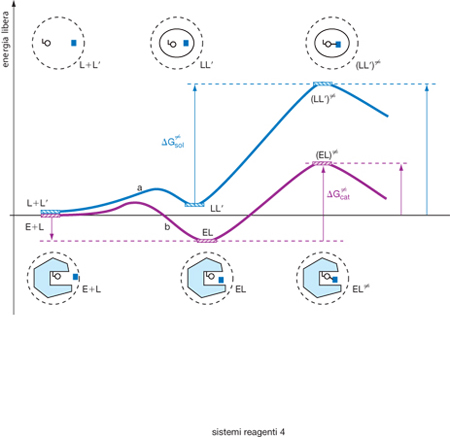
Molte reazioni biologiche sono catalizzate dagli enzimi, cioè da proteine nella cui configurazione spaziale sono presenti centri attivi alla cui complementarietà morfologica con il reagente viene attribuita l'azione catalitica stessa. Anche se le ricerche nel settore della biochimica strutturale hanno permesso di evidenziarne le caratteristiche, il meccanismo delle reazioni catalizzate dagli enzimi presenta ancora aspetti non compresi, in particolare il fatto che la loro costante di velocità di reazione sia molto più elevata di quella che si misura quando la reazione avviene in una gabbia di solvente. In altri termini, come illustrato nella fig. 3, la barriera di attivazione ΔG# è molto più piccola del valore corrispondente. Ciò era già stato stabilito da L.C. Pauling nel 1946, senza però chiarire del tutto quale ne fosse la causa. Viene ormai attribuito o a impedimenti sterici presenti nello stato fondamentale del reagente che si allentano nel complesso attivato o all'interazione elettrostatica fra il reagente e il centro attivo enzimatico.
È comunque importante ricordare che nelle cellule gli enzimi raramente operano da soli, viceversa essi sono associati a parti attive non proteiche chiamate coenzimi con i quali sono organizzati in complesse reti di reazioni catalitiche.
Interazione fra cinetica e diffusione
Una delle caratteristiche peculiari dei s. r. c. si manifesta in una sequenza di comportamenti che vanno dagli stati stazionari omogenei, stabili e instabili, a strutture ordinate nel tempo e nello spazio che possono però degenerare in comportamenti caotici. Questi ultimi casi sono dovuti alla competizione fra la velocità delle reazioni chimiche e quella dei processi diffusivi. Per comprendere perché ciò possa dare origine a configurazioni ordinate è opportuno riferirsi al semplice modello di due celle. Esse vengono entrambe alimentate con il flusso ϕ di un componente che si trasforma in una reazione chimica e che si può diffondere da una cella all'altra con una velocità proporzionale alla differenza di concentrazione che esiste fra le due celle. Se si indica con C1 e C2 le concentrazioni nelle due celle e si assume per semplicità che la velocità di reazione sia espressa da una equazione cinetica lineare del tipo kC, è facile dimostrare che le equazioni di bilancio si possono scrivere come segue:
✄
✄
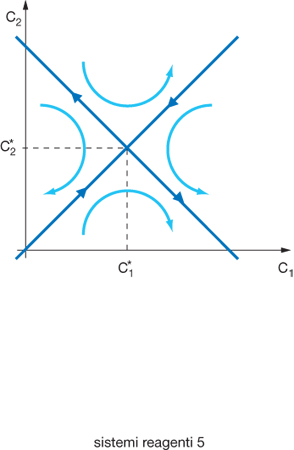
dove K è il coefficiente di accoppiamento diffusivo. È facile verificare che il precedente sistema di equazioni presenta uno stato stazionario con ✄, mentre gli esponenti di Liapunov hanno i seguenti valori: σ1=−k (sempre negativo), σ2=2K−k (negativo se K⟨k/2); per cui gli stati stazionari risultano stabili se il coefficiente K risulta inferiore alla metà della costante di velocità di reazione. Se lo stato risulta instabile e il suo comportamento viene rappresentato su un diagramma in cui viene espressa l'evoluzione delle concentrazioni, si ottengono le traiettorie riportate nella fig. 4, che finiscono in due punti rispettivamente con valori nulli della concentrazione in una delle due celle, e di conseguenza con il componente accumulato nell'altra. In sostanza, pur avendo preso in considerazione una situazione molto semplificata, ne emerge che si genera in modo autonomo una polarizzazione con una rottura della simmetria rispetto alla situazione corrispondente alla soluzione stabile nella quale il componente è distribuito in modo uniforme in entrambe le celle. In altri termini, da un mezzo uniforme, e di conseguenza del tutto simmetrico, si generano configurazioni spazio-temporali meno simmetriche ma ben più organizzate. Per fare riferimento a una situazione più realistica appare opportuno considerare un sistema continuo ove esistano almeno 2 reagenti A, e B, con concentrazioni CA e CB, che si trasformano con leggi cinetiche non lineari dipendenti da entrambe le concentrazioni e si diffondono con coefficienti di diffusione diversi. In questo caso il comportamento del sistema viene matematicamente descritto da un sistema di due equazioni differenziali del tipo:
✄
dove f(CA, CB) e g(CA, CB) esprimono le velocità di trasformazione di A e B rispettivamente, mentre DA e DB sono i loro coefficienti di diffusione. L'operatore ∇2 è il laplaciano, tale per cui ∇2C risulta proporzionale alla differenza fra il valore medio della concentrazione valutata nell'immediato intorno di un punto e il valore della concentrazione nel punto stesso. Le precedenti costituiscono un sistema di equazioni differenziali di secondo ordine alle derivate parziali, solitamente non lineari per la forma delle velocità di reazione. Le condizioni al contorno riflettono le caratteristiche dei flussi di ingresso e di uscita delle specie in corrispondenza della superficie che separa il sistema in esame dall'ambiente circostante. La sua integrazione deve essere perseguita fruendo delle tecniche di calcolo numerico.
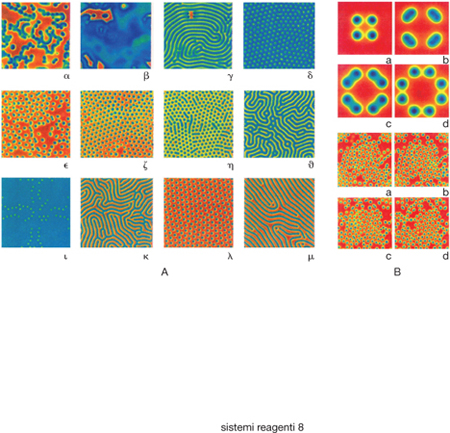
Nell'impostazione precedente rientra un modello classico, dovuto a A.M. Turing, formulato per giustificare i processi di formazione di configurazioni morfologiche ordinate che si manifestano nei sistemi biologici, attribuendoli a opportune sostanze chimiche, chiamate morfogeni, che agiscono sulle velocità delle reazioni presenti nel sistema. Questa ipotesi, che al suo enunciato era stata accolta con diffidenza da alcuni biologi, ha trovato successivamente conferme dalla scoperta di particolari proteine che agiscono quali regolatrici di geni. Si considera un sistema nel quale ha luogo una competizione fra una specie a che opera a corto raggio e una specie inibitrice h che agisce a lungo raggio, interagenti con dinamiche di retroazione. La soluzione delle corrispondenti equazioni differenziali di bilancio descrive l'evoluzione del sistema verso stati stabili non omogenei caratterizzati da particolari configurazioni spaziali delle concentrazioni.
In un altro esempio si assume che le trasformazioni chimiche seguano uno schema cinetico del tipo:
A+2X→3X; X→ B.
In esso è presente un effetto autocatalitico poiché la specie X prodotta nella prima reazione aumenta la velocità della reazione stessa. L'espressione matematica di tale velocità non è lineare poiché è proporzionale al prodotto della concentrazione della specie A per il quadrato della concentrazione della specie intermedia X. Si ottiene una gamma articolata di soluzioni dipendenti dal valore del flusso di alimentazione e dalla costante di velocità k, che risultano stabili e uniformi o che presentano due stati stabili non uniformi aventi le configurazioni spaziali riportate nella fig. 5 B. L'approccio precedente, se pure semplificato, viene invocato per interpretare i fenomeni morfogenici, ovvero generanti strutture, che hanno luogo negli organismi viventi. Si assume infatti che i processi metabolici e di crescita coinvolgano molecole segnale che agiscono su opportuni siti regolatori esaltando l'attività di nuovi geni e reprimendone altri, e dando così origine a meccanismi di retroazione positivi e negativi in accordo al modello di Turing. In sostanza, anche se l'approccio appare un poco semplificato, offre un serio contributo all'analisi dei fenomeni menzionati per la sua capacità di generare forme realistiche a partire da uno stato iniziale pressoché uniforme.
Reti di reazioni biologiche
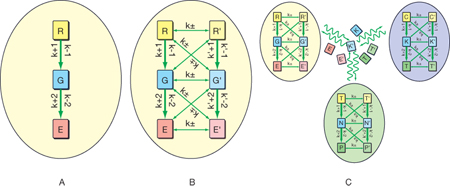
Uno dei più importanti processi operanti negli organismi viventi è il metabolismo mediante il quale ha luogo la trasformazione di materie prime attinte dall'ambiente nelle molecole richieste alle cellule, producendo nel contempo l'energia che è necessaria. Sono infatti presenti reazioni sequenziali e accoppiate cui prendono parte composti chiamati metaboliti. Attraverso complesse interazioni come quelle illustrate nella fig. 6, si generano delle reti costituite da geni e proteine riflettenti la presenza di cammini di interazione preferenziali (signaling). Si tratta di vere e proprie architetture costruite su nodi formati da particolari molecole che interagiscono reciprocamente. Queste interazioni molecolari, geneticamente programmate, condizionano il controllo e lo sviluppo delle cellule stesse; inoltre possono manifestare interessanti proprietà emergenti caratterizzate dalla comparsa di comportamenti non prevedibili dalle proprietà dei singoli componenti presenti nel sistema. Tipica è l'insorgenza di cicli di retroazione i quali possono comportarsi alla stregua degli interruttori per il controllo del flusso di informazione.
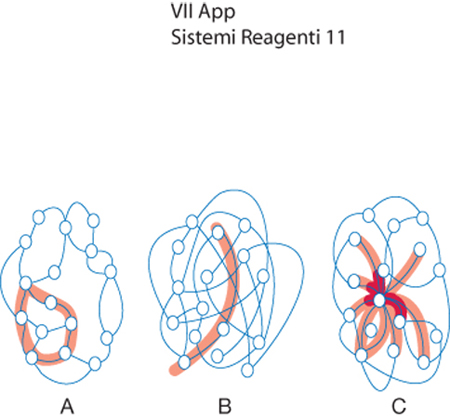
Per individuare una strategia di indagine è opportuno riferirsi alla teoria statistica delle reti, rappresentandole al pari di un insieme di sottounità o nodi che interagiscono o comunicano fra loro. Tutto ciò senza richiedere la presenza di una struttura metrica speciale che attribuisca ai nodi una posizione nello spazio ben definita. Ogni nodo viene connesso mediante k legami agli altri e il modo con cui vengono attuati i legami condiziona il comportamento della rete. Infatti, come viene illustrato in fig. 7, esse possono essere: regolari, qualora siano presenti gruppi locali di nodi interconnessi, casuali, se sono assenti gruppi di nodi ma la rete è facilmente attraversabile, a scala libera (scale free), se la rete è facilmente attraversabile pur esistendo dei gruppi di nodi interconnessi.
Qualora si assuma che nel corso dell'evoluzione della rete tutti i nodi risultino equivalenti e anche accessibili, e che si uniscono ad altri con uguale probabilità mantenendo il loro numero inalterato durante la vita della rete stessa, la probabilità che un nodo scelto a caso abbia un numero k di interconnessioni risulta espressa da:
✄
essendo il numero medio di legami, o anche scala della rete. La precedente costituisce una tipica distribuzione di Poisson rispetto al numero medio di nodi ed è caratteristica delle cosiddette reti di Erdos-Renyi.
Molto spesso però non è possibile attribuire alla rete una scala specifica per cui la probabilità risulta espressa da una legge di potenza del tipo:
p(k)∝ kγ, (γ =1,2,3).
La validità di questa relazione è stata riscontrata, anche empiricamente, nella descrizione di sistemi non solo di interesse chimico e biologico ma anche ecologico, economico e sociale. Può essere giustificata in diversi modi, in particolare assumendo che l'evoluzione della rete proceda con l'aggiunta a intervalli regolari di tempo di un nuovo nodo e che ciascun nodo si connetta con gli altri con una probabilità proporzionale al numero di nodi che già possiede. La descrizione dell'evoluzione della rete, effettuata mediante una serie di equazioni simili a quelle impiegate per studiare quella dei prodotti di una serie di reazioni successive, giustifica un comportamento compatibile con una relazione a scala libera.
L'analisi sperimentale di decine di reti metaboliche riferite a diversi organismi, che vanno dai batteri alle piante, ha confermato che la connettività della loro distribuzione è del tipo a scala libera. Per approfondire questo importante risultato si può osservare che le migliaia di reazioni enzimatiche, che danno luogo ai flussi metabolici, possono essere esplorate con i metodi della cinetica chimica, traendo vantaggio dal fatto che esse esercitano un controllo sia dei flussi energetici sia della produzione dei componenti cellulari che entrano nel metabolismo. La formulazione di uno schema delle diverse reazioni che intervengono nel processo risulta purtroppo indeterminata, poiché se ne possono proporre differenti in grado di descrivere la formazione dei composti in gioco. Per fare una scelta si assume che i flussi metabolici soddisfino alle condizioni di stazionarietà e nel contempo si impone che la velocità di produzione della biomassa, che contribuisce alla crescita del sistema ed è espressa attraverso una combinazione lineare dei flussi metabolici, sia massima (flux balance analysis).
L'analisi dei dati sperimentali rivela però una mancanza di omogeneità nella distribuzione dei flussi poiché alcuni di essi prevalgono nettamente sugli altri e al limite può risultare che una singola reazione domini la trasformazione di alcuni metaboliti. Questo risultato è compatibile con il fatto che la rete che descrive l'insieme delle reazioni metaboliche è invariante rispetto alla scala. La mancanza di omogeneità fra i flussi riflette anche la presenza di una struttura del sistema, poiché i collegamenti fra le diverse reazioni soddisfano particolari topologie. Questo interessante risultato fa sorgere la domanda se esso costituisca un riflesso della storia evolutiva del metabolismo. La potenziale relazione fra la storia evolutiva e la connettività delle reti metaboliche corrobora un postulato avanzato da H. Morowitz in base al quale si assume che il metabolismo intermedio ricapitola l'evoluzione della biochimica.
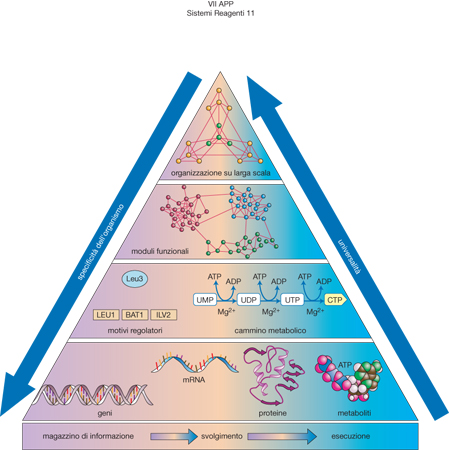
Più in generale, se le cellule e i microrganismi sono visti come una rete di geni e proteine, si può individuare una strategia per affrontare la complessità degli organismi viventi, sintetizzata con la piramide illustrata nella fig. 8, in cui i moduli presenti nella parte inferiore si distribuiscono in una struttura gerarchica che definisce l'organizzazione funzionale delle cellule sulle scale crescenti.
bibliografia
J. Villa, A. Warshel, Energetics and dynamics of enzymatic reactions, in Journal of physical chemistry B, 2001, 105, pp. 7887-907; R. Albert, A.-L. Barabási, Statistical mechanics of complex networks, in Review of modern physics, 2002, 74, pp. 47-97; J. Watson, DNA, The secret of life, Londra 2003 (trad. it. Milano 2006).