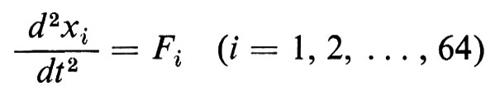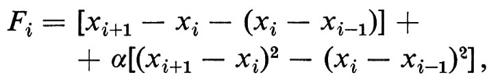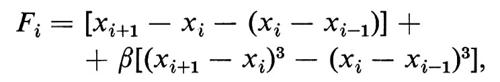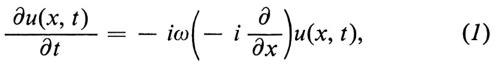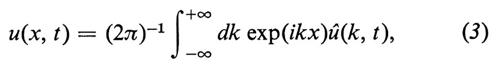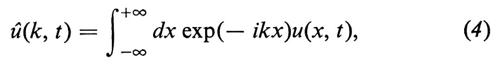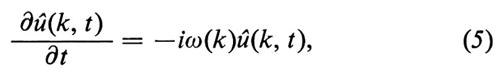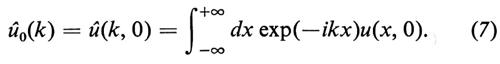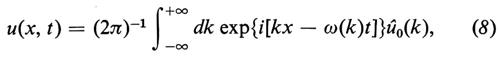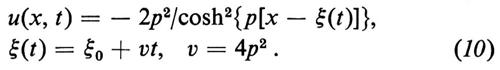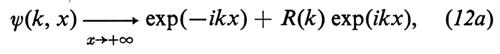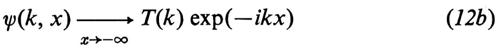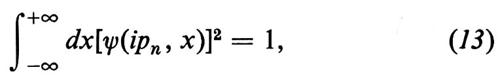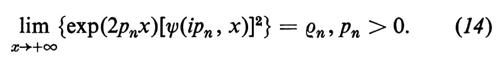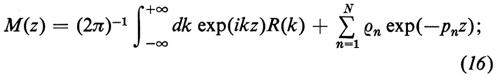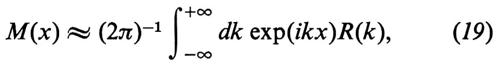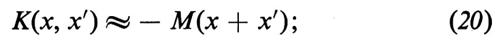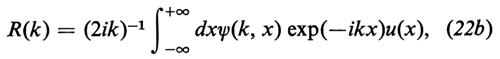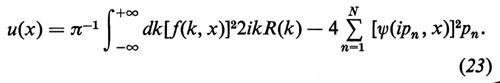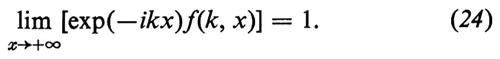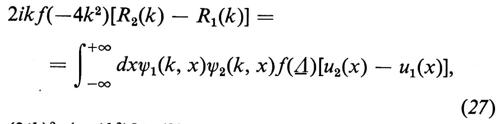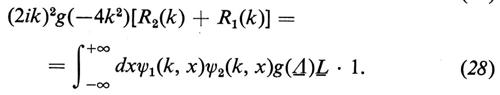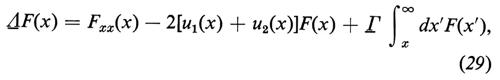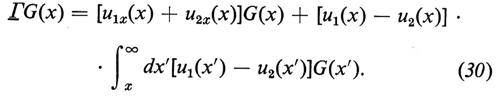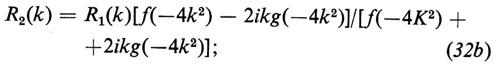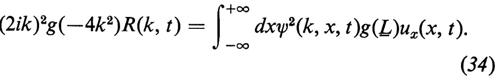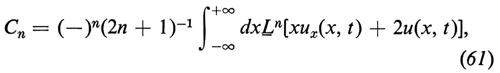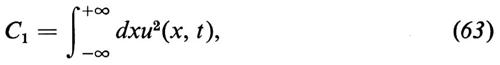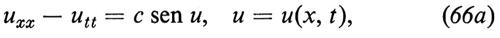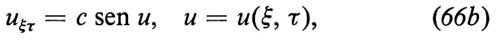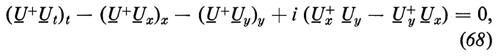Solitoni

Solitoni

SOMMARIO: 1. Introduzione: cenno storico.  2. Soluzione di equazioni lineari di evoluzione mediante la trasformata di Fourier.  3. L'equazione di Korteweg-de Vries.  4. La trasformata spettrale: a) il problema spettrale di Schrödinger; b) relazione fra cambiamenti della funzione u(x) e cambiamenti della sua trasformata spettrale; c) evoluzione temporale; classe delle equazioni integrabili.  5. Solitoni e solitroni.  6. Leggi di conservazione.  7. Altre tecniche per lo studio di equazioni di evoluzione integrabili.  8. Altre equazioni risolubili.  9. Applicazioni. □ Bibliografia.

1. Introduzione: cenno storico

‟Stavo osservando il moto di una barca trascinata lungo un canale da una coppia di cavalli, quando la barca si è arrestata improvvisamente - non così la massa d'acqua che la barca aveva messo in moto, che si è accumulata vicino alla prua del battello in uno stato di violenta agitazione, e poi lo ha improvvisamente lasciato indietro, rotolando in avanti con grande velocità e assumendo la forma di una grande elevazione solitaria, un ammasso d'acqua di forma arrotondata, liscia e ben definita, che ha continuato il suo cammino lungo il canale senza visibile cambiamento di forma o diminuzione di velocità. L'ho seguito a cavallo, e l'ho raggiunto che continuava a procedere a una velocità di 8 o 9 miglia l'ora, conservando la sua forma originaria lunga circa 30 piedi e alta da un piede a un piede e mezzo. La sua altezza è diminuita gradatamente, e dopo un inseguimento di una o due miglia l'ho perso di vista nelle curve del canale. Tale, nel mese di agosto del 1834, è stato il mio primo casuale incontro con questo singolare e bel fenomeno [...]".

Questa descrizione particolarmente dettagliata si riferisce alla prima osservazione scientifica di un ‛solitone', compiuta da J. Scott Russell, un geniale ingegnere britannico vissuto nell'era vittoriana, il quale ha dedicato parte della sua vita proprio allo studio di questi fenomeni (v. Scott Russell, 1845).

Un ulteriore importante progresso per la comprensione di questi fenomeni è stato compiuto alla fine del secolo scorso, quando fu scritta un'equazione differenziale alle derivate parziali non lineare, descrivente l'evoluzione temporale del profilo di un fluido in un canale poco profondo (v. Korteweg e de Vries, 1895). Questa equazione di Korteweg-de Vries, o, come si usa ora chiamarla in forma abbreviata, equazione KdV, verrà discussa in dettaglio nel seguito, poiché essa offre il mezzo più conveniente per illustrare le proprietà matematiche dei solitoni e tutta quella fenomenologia teorica che si riallaccia a tali proprietà. Per il momento basterà osservare che l'equazione KdV ammette per l'appunto, come vedremo, una particolare soluzione che rappresenta proprio una singola onda ‟di forma arrotondata, liscia e ben definita", che trasla ‟senza visibile cambiamento di forma o diminuzione di velocità".

Questa proprietà dell'equazione KdV, come del resto la stessa esistenza di tale equazione come appropriata descrizione di fenomeni naturali, è stata però largamente negletta nella prima metà di questo secolo, presumibilmente a causa della mancanza di strumenti matematici idonei allo studio sistematico e praticabile delle equazioni di evoluzione alle derivate parziali non lineari; in particolare per la mancanza di qualunque metodologia matematica che andasse oltre l'eventuale determinazione di teoremi di esistenza e unicità delle soluzioni, per permettere anche una comprensione qualitativa del comportamento delle soluzioni stesse. E ciò in marcato contrasto con la teoria delle equazioni di evoluzione alle derivate parziali lineari, per le quali la tecnica basata sulla trasformata di Fourier - inventata del resto proprio per risolvere l'equazione, lineare, di propagazione del calore (v. Fourier, 1822) - fornisce, come vedremo, una trasparente metodologia che permette di interpretare l'evoluzione temporale delle soluzioni in termini di velocità di fase, dispersione, velocità di gruppo.

È stato solo negli anni sessanta di questo secolo che l'equazione KdV ha ripreso a essere considerata interessante, non tanto in idrodinamica, quanto in fisica dei plasmi, nonché per la sua connessione con il paradosso di Fermi, Pasta e Ulam (v., 1965).

Il paradosso di Fermi, Pasta e Ulam consiste nell'inatteso risultato di un esperimento numerico, reso possibile dai calcolatori elettronici, che cominciarono a essere disponibili per il calcolo scientifico all'inizio degli anni cinquanta. Si tratta dello studio del comportamento di una catena unidimensionale di oscillatori, accoppiati con i primi vicini in modo non lineare (quadratico o cubico), studio compiuto integrando numericamente le equazioni del moto newtoniane

di un sistema costituito da 64 particelle identiche di massa unitaria. In queste equazioni

oppure

a seconda che si tratti del caso quadratico o di quello cubico. Ricordiamo che, nel caso di accoppiamento lineare (oscillatori armonici), tali equazioni del moto possono essere disaccoppiate mediante l'introduzione, come nuove variabili dinamiche (‛modi normali'), di opportune combinazioni lineari delle x_i; pertanto la soluzione generale delle equazioni del moto, nel caso lineare, si riduce a una sovrapposizione di moti armonici, e l'evoluzione temporale complessiva ha carattere multiplamente periodico, con la quantità di energia associata a ciascuna componente periodica che rimane costante nel tempo. Nel caso non lineare, invece, il moto non potrà generalmente risultare multiplamente periodico, in quanto i termini di accoppiamento non lineare possono dar luogo alla creazione di ulteriori frequenze (nonché al trasferimento di energia da una frequenza all'altra). Il comportamento che ci si attendeva, sulla base di concetti fondamentali della meccanica statistica (principio di equipartizione dell'energia), era una progressiva stocasticizzazione del moto, con l'apparizione di componenti di frequenza sempre più alta e una diffusione dell'energia su tali frequenze.

L'esperimento numerico mostrò invece che, se si partiva da una configurazione iniziale in cui l'energia era tutta concentrata nel modo normale più basso (quello cioè che sarebbe stato il modo normale di oscillazione a più lungo periodo, in assenza dei termini di accoppiamento non lineare), essa tendeva in effetti a ripartirsi negli altri modi normali sui tempi brevi, ma in un successivo istante si verificava un'inattesa ‛ricorrenza', in cui l'energia si trovava nuovamente concentrata quasi completamente nel modo iniziale (v. fig. 1).

Nel tentativo di risolvere questo problema M. D. Kruskal (v. Zabusky e Kruskal, 1965) fu ricondotto allo studio dell'equazione KdV, che rappresenta un'approssimazione continua alla catena di oscillatori investigata da Fermi, Pasta e Ulam (caso quadratico), e che d'altra parte interviene nella descrizione di alcuni fenomeni di instabilità del plasma, il cui studio aveva nel frattempo acquisito grande importanza in connessione col tentativo di realizzare la fusione nucleare controllata.

In effetti una spiegazione del fenomeno osservato da Fermi, Pasta e Ulam può essere data sulla base delle proprietà dell'equazione KdV; ma si tratta di una spiegazione alquanto indiretta, anche se in ultima analisi riconducibile alla possibilità di ‛linearizzare' l'equazione KdV mediante la tecnica della trasformata spettrale, su cui torneremo in dettaglio più innanzi. Dal punto di vista di questo rapido cenno storico, quel che importa rilevare è che la ripresa di interesse per l'equazione KdV portò a ulteriori importanti scoperte e invenzioni, compresa l'introduzione del concetto (e del termine) di ‛solitone'.

Abbiamo già detto come l'equazione KdV ammetta delle speciali soluzioni che sono localizzate, hanno una ben definita forma e viaggiano con velocità costante. Si supponga ora di partire da una condizione iniziale in cui si hanno due siffatte configurazioni, localizzate intorno a due punti molto lontani l'uno dall'altro e disposte in modo che le velocità caratteristiche di ciascuna di esse le portino, una volta iniziato il moto, a incontrarsi. È allora chiaro che, nella fase iniziale del moto, cioè fino a che le due onde localizzate sono così distanti l'una dall'altra da non interferire, ciascuna di loro viaggerà con velocità costante, senza cambiare di forma. Ma a un certo punto le due configurazioni si sovrapporranno, magari perdendo completamente la loro identità (cioè per un certo intervallo di tempo il profilo potrà registrare un solo massimo anziché due). Quel che però si scoprì, ancora una volta mediante un esperimento numerico (v. Zabusky e Kruskal, 1965), è che sempre, dopo la collisione, le due onde riacquistano la loro identità, e unico effetto della collisione è quello di provocare uno spostamento della loro posizione rispetto a quella che avrebbero avuto se avessero continuato a viaggiare indisturbate: dopo l'urto la soluzione dell'equazione KdV rappresenta nuovamente un profilo che è la somma delle stesse due onde localizzate che si avevano all'inizio, ciascuna delle quali viaggia con la sua caratteristica velocità; di modo che, essendosi ora l'ordine delle due onde invertito (la collisione ha dato luogo a uno scavalcamento), come prima dell'urto le due onde andavano avvicinandosi, così dopo l'urto si allontanano indefinitamente (v. fig. 2). In effetti i risultati numerici di Zabusky e Kruskal si riferivano al caso dell'equazione KdV su un intervallo spaziale di lunghezza finita con condizioni periodiche agli estremi, anziché al caso, più semplice dal punto di vista teorico ma più difficile da trattare numericamente, di intervallo infinito, cui si riferiscono la precedente descrizione e le immagini della fig. 2. Ma quando il fenomeno della collisione di due solitoni avviene sufficientemente lontano dai bordi, non vi è sostanziale differenza fra i due casi.

Il fenomeno della persistenza dei solitoni dopo l'urto è ben visibile quando l'evoluzione temporale dell'equazione KdV, calcolata numericamente, viene mostrata mediante un film (che è per l'appunto quello che hanno fatto Zabusky e altri ricercatori), ed è forse il caso di sottolineare che questo comportamento è assai sorprendente; come vedremo in seguito (v. cap. 5), vi sono molte altre equazioni, analoghe all'equazione KdV, che ammettono anch'esse soluzioni tipo ‛onda solitaria', ma per le quali la collisione di due siffatte onde dà luogo a una fenomenologia molto più complicata.

Il concetto, e il termine, di ‛solitone' fu per l'appunto introdotto (v. Zabusky e Kruskal, 1965) per denotare queste entità localizzate che si manifestano nelle soluzioni dell'equazione KdV (e, come vedremo, anche di altre speciali equazioni) e che hanno la proprietà di ritrovarsi inalterate dopo le collisioni; il che suggerisce che esse abbiano sempre una loro esistenza e identità, anche in quegli istanti durante l'urto in cui se ne perde ogni traccia visibile. Evidentemente il termine ‛solitone' sottolinea tutto ciò grazie alla sua analogia con i nomi delle particelle elementari (elettrone, positrone, ecc.).

Questa fenomenologia, unita alla rilevanza dell'equazione KdV dal punto di vista applicativo, motivò uno studio di questa equazione da parte di un gruppo di fisici teorici (C. S. Clardner, J. M. Greene, M. D. Kruskal e R. M. Miura), i quali si trovavano in quel momento tutti a lavorare presso il grande laboratorio di Princeton di fisica del plasma e per la fusione. Cominciarono così a emergere altre rimarchevoli proprietà dell'equazione KdV, a cominciare dall'esistenza di un numero infinito di costanti del moto, cioè grandezze costruite a partire da una qualunque soluzione dell'equazione KdV, che risultano essere costanti nel tempo (nonostante la soluzione stessa vari nel tempo, come prescritto dalla stessa equazione KdV).

Ma la scoperta di gran lunga più importante (o forse si dovrebbe parlare di invenzione?) è stata quella di un metodo (v. Gardner e altri, 1967) per risolvere l'equazione KdV, il cosiddetto ‛metodo della diffusione inversa' o, più propriamente, della ‛trasformata spettrale'; metodo che verrà descritto in qualche dettaglio più innanzi. Tale metodo dà conto delle proprietà peculiari dell'equazione KdV che abbiamo descritto, e di altre di cui diremo più oltre, e chiarisce tutta la fenomenologia associata ai solitoni, che non solo risultano essere presenti nelle speciali soluzioni che descrivono uno o più solitoni (soluzioni la cui forma analitica è ora nota esplicitamente), ma costituiscono una componente precisamente identificabile della generica soluzione dell'equazione KdV corrispondente a una larga classe di condizioni iniziali.

L'importanza della trasformata spettrale è principalmente dovuta al fatto che essa fornisce una tecnica di soluzione, che estende ad alcune classi di equazioni ‛non lineari' una metodologia analoga a quella fornita dallo sviluppo in serie e integrale di Fourier per equazioni ‛lineari'. Nel giro di qualche anno si è visto che tale tecnica è applicabile non solo all'equazione KdV, e non solo a un'intera classe di equazioni che include come primo più semplice esempio l'equazione KdV, ma anche a molte altre classi di equazioni non lineari di evoluzione, nelle quali sono incluse numerose equazioni di grande interesse applicativo, quali l'equazione di Schrödinger non lineare, la cosiddetta ‛equazione di seno-Clordon', l'equazione che descrive l'interazione di tre onde, e molte altre cui accenneremo in seguito (v. cap. 8).

Negli ultimi anni un'intensa e fruttuosa attività di ricerca è stata per l'appunto diretta a estendere le classi di equazioni risolubili mediante questa tecnica. Si sono così scoperti anche nuovi fenomeni, come per esempio delle equazioni non lineari di evoluzione con solitoni che non si muovono con velocità costante, ma come particelle sottoposte a forze (‛bumeroni', ‛trapponi', ‛zumeroni'; v. Calogero e Degasperis, 1982-1987, vol. II), nonché la risolubilità, mediante la tecnica della trasformata spettrale, anche di equazioni, quale per esempio la cosiddetta equazione KdV ‛cilindrica' (di interesse applicativo nella fisica dei plasmi e della fusione), che non posseggono nessuna soluzione di tipo solitonico e che dunque non ci si sarebbe a priori attesi fossero trattabili con queste tecniche (v. Calogero e Degasperis, 1982-1987, vol. I).

Sembra dunque che il metodo della trasformata spettrale abbia aperto la prospettiva di un approccio sistematico alla soluzione di equazioni non lineari di evoluzione. Naturalmente questa tecnica è applicabile solo ad alcune classi di tali equazioni; nè potrebbe essere altrimenti, essendo l'universo delle equazioni non lineari, per la sua stessa definizione, senza confini, sicché nessuna tecnica matematica potrà mai sperare di esaurirlo.

Senza dubbio le equazioni trattabili con questa tecnica rappresentano una classe alquanto eccezionale, che però sembra includere un numero sorprendentemente grande di equazioni di interesse applicativo, almeno nel campo delle equazioni alle derivate parziali in due variabili (una temporale e una sola spaziale, o, in qualche caso, due variabili spaziali). L'estensione di questa o di analoghe tecniche al caso di equazioni in più di due variabili è invece ancora allo stato embrionale, anche se vi sono dei casi, anche importanti dal punto di vista applicativo, in cui è stata possibile; per esempio per le equazioni, in due dimensioni spaziali e una temporale, di Kadomcev-Petvjašvili e di Davey-Stewardson e per le equazioni (ridotte) di Yang e Mills, nonché per le equazioni delle tre onde risonanti in tre dimensioni spaziali e una temporale (v. Calogero e Degasperis, 1982-1987, vol. I).

Nei successivi capitoli si descriverà la tecnica della trasformata spettrale e la fenomenologia solitonica, usando come principale esempio l'equazione KdV e seguendo, talvolta verbatim, precedenti trattazioni (v. Calogero, 1979; v. Calogero e Degasperis, 1982-1987, vol. I). Il punto di partenza è l'analogia fra la tecnica della trasformata spettrale, che si dimostra efficace per risolvere alcune classi di equazioni non lineari di evoluzione, e la tecnica della trasformata di Fourier, che è invece appropriata alla soluzione delle equazioni lineari (anche questa tecnica viene succintamente ricordata: v. cap. 2). Negli ultimi tre capitoli si accennerà rispettivamente alle altre tecniche per lo studio di queste classi di equazioni di evoluzione, alle altre equazioni e classi di equazioni trattabili con queste tecniche e infine al vasto campo delle applicazioni.

2. Soluzione di equazioni lineari di evoluzione mediante la trasformata di Fourier

Si consideri l'equazione (alle derivate parziali) di evoluzione

dove ω(z) è un polinomio e i l'unità immaginaria. Un problema tipico della fisica matematica, e più generalmente della matematica applicata, è quello in cui la funzione u è assegnata all'istante iniziale,

u(x, 0) = u₀(x), (2)

e si tratta di studiarne la successiva evoluzione (problema di Cauchy). Si assumerà sempre che la funzione incognita sia definita per ogni valore di x e si annulli (abbastanza rapidamente) per x → ± ∞.

La soluzione del problema si ottiene introducendo la trasformata di Fourier (nella variabile x) della u(x, t) mediante le formule:

che instaurano una corrispondenza biunivoca fra le funzioni u(x, t) e û(k, t). All'evoluzione (1) per la u(x, t) corrisponde la semplice evoluzione:

che può essere immediatamente integrata. Si ottiene così

û(k, t) = u₀(k) exp[−iω(k)t], (6)

dove

Il problema dell'evoluzione temporale della u(x, t) è dunque esplicitamente risolto con tre passaggi: 1) al tempo iniziale si determina la trasformata di Fourier û(k, 0) a partire dalla funzione assegnata u(x, 0) (usando la 7); 2) la trasformata di Fourier evolve nel tempo, a partire dalla û(k, 0), secondo la semplice ed esplicita formula (6); 3) al tempo t si ricostruisce la u(x, t) a partire dalla sua trasformata di Fourier (usando la 3). La formula finale, che riassume in modo compatto il risultato,

indica chiaramente come l'evoluzione temporale della u(x, t) sia determinata dalla ‛funzione di dispersione' ω(k).

Particolarmente notevole è il caso in cui il polinomio ω(z) è reale e dispari (ω(− z) = − ω(z)); in tal caso la (1) è reale, e la (6) implica û(k, t) ∣ = ∣ û(k, 0) , sicché non vi è dissipazione (caso puramente dispersivo).

La tecnica di soluzione si fonda dunque sulla possibilità di scomporre la funzione u(x, t) nelle sue componenti di Fourier, û(k, t) exp(ikx), e sul fatto che, quando la u(x, t) evolve secondo l'equazione alle derivate parziali lineare a coefficienti costanti (1), le sue componenti di Fourier subiscono semplicemente una traslazione uniforme, ciascuna con la propria ‛velocità di fase' ω(k)/k (v. 6 e 8). Il fatto che la velocità di fase vari al variare di k (salvo nel caso eccezionale ω(z) = cz) dà luogo al fenomeno della ‛dispersione'; sicché una soluzione (‛pacchetto d'onde'), la cui trasformata di Fourier sia concentrata intorno al valore k₀, tende a viaggiare, almeno per tempi grandi, con la ‛velocità di gruppo' ω′(k₀)(ω′(z) ≡ dω(z)/dz), e a ‛disperdersi' (nel caso, qui discusso, di una sola dimensione spaziale, il suo massimo modulo,

va calando proporzionalmente a t−½).

La tecnica di soluzione della (1) mediante la trasformata di Fourier, anche se non sempre può essere esplicitamente implementata (perché non è detto che gli integrali (7) e (8) possano essere esplicitamente calcolati) fornisce comunque una comprensione qualitativa del comportamento delle soluzioni della (1). Il principale insegnamento che discende da questa tecnica di soluzione della (1) è che l'evoluzione temporale è molto più semplice nello spazio di Fourier (cioè per la funzione û(k, t)), che nello spazio delle configurazioni (cioè per la funzione u(x, t)), ancorché le due rappresentazioni siano equivalenti, stante la corrispondenza biunivoca instaurata dalle (3) e (4). Pertanto ogni tentativo di comprensione (anche sperimentale) del fenomeno naturale schematizzato dalla (1) andrà preferibilmente compiuto, o comunque ricondotto, nel contesto dello spazio di Fourier (variabile k) anziché nel contesto dello spazio delle configurazioni (variabile x). È questo il messaggio fondamentale, e di grandissima importanza teorica e pratica, che conclude questa succinta analisi.

3.L'equazione di Korteweg-de Vries

Scriviamo l'equazione KdV nella forma convenzionale

u_t + u_xxx − 6u_xu = 0, u ≡ u(x, t) (9)

in cui la derivazione parziale rispetto a t o a x è indicata apponendo la rispettiva variabile, come indice, alla funzione; per esempio

Questa equazione corrisponde a quella scritta originariamente (v. Korteweg e de Vries, 1895), salvo che per il passaggio a variabili adimensionali, e l'omissione di un termine cu_x a primo membro, che è stato eliminato mediante il cambiamento di variabile x → x′ = x − ct, equivalente al passaggio a un sistema di riferimento in moto uniforme con velocità c nel verso positivo dell'asse x. Il fatto che questa equazione sia del primo ordine nella derivata rispetto al tempo, e non sia pertanto invariante rispetto al verso di scorrimento del tempo, origina dal fatto che essa è appropriata alla descrizione (approssimata) del moto di perturbazioni (per esempio onde di superficie in un canale poco profondo) propagantisi complessivamente in un verso definito (quello delle x crescenti).

Come si può verificare per sostituzione, l'equazione (9) ammette la soluzione

Si tratta in effetti di una famiglia di soluzioni, che è caratterizzata da due parametri: ξ₀, che ne fissa la posizione al tempo t = 0; p (convenzionalmente, un numero reale positivo), che fissa la ‛forma' della soluzione (tanto il massimo modulo, 2p², che la larghezza, inversamente proporzionale a p) nonché la ‛velocità', 4p², con cui la soluzione trasla di moto uniforme nel verso delle x crescenti.

È chiaro che questa soluzione corrisponde piuttosto fedelmente alla descrizione di Scott Russell riportata in apertura di questo articolo; si immagini in particolare che la u(x, t) rappresenti l'altezza del pelo dell'acqua nel punto x al tempo t, misurata, rispetto al livello del fluido in quiete, in un sistema di riferimento diretto verso il basso (ed eventualmente in moto rettilineo uniforme con velocità c: v. sopra). Pur essendo la (10) una soluzione particolare della (9), vedremo che, in un senso che preciseremo, contributi di questo tipo sono presenti nella soluzione generica dell'equazione KdV (9).

È forse il caso di sottolineare che, a causa del fenomeno della dispersione, nessuna equazione ‛lineare' del tipo (1) (salvo la banale equazione del primo ordine, u_t + cu_x = 0, con soluzione u(x, t) = u(x − ct, 0)) può avere soluzioni che traslano senza cambiare di forma, come fa invece la (10). Per l'esistenza del solitone gioca dunque un ruolo essenziale la non linearità; in effetti è giustificato pensare che la soluzione (10) corrisponda a un preciso equilibrio fra l'effetto del termine dispersivo u_xxx e l'effetto del termine non lineare uu_x nella (9); se il termine non lineare fosse assente, il massimo modulo della soluzione tenderebbe ovunque a zero per t → ∞; se invece mancasse il termine dispersivo, la soluzione potrebbe sviluppare una singolarità nella derivata (‛shock') in un tempo finito.

4. La trasformata spettrale

Nel cap. 2 abbiamo introdotto la trasformata di Fourier e abbiamo indicato come essa serva per risolvere l'equazione di evoluzione lineare (1). In questo capitolo introduciamo la trasformata spettrale e mostriamo come essa, in modo analogo, permetta di risolvere l'equazione KdV (anzi un ‛intera classe di equazioni non lineari' di evoluzione, comprendente l'equazione KdV come primo esempio non banale).

a) Il problema spettrale di Schrödinger.

Punto di partenza è il problema spettrale caratterizzato dall'equazione di Schrödinger indipendente dal tempo per problemi unidimensionali, che scriveremo

− ψ_xx(k, x) + u(x)ψ(k, x) = k²ψ(k, x). (11)

Di nuovo si assumerà sempre che la funzione u(x) si annulli (abbastanza rapidamente) per x → ± ∞. È importante sottolineare a questo punto che le successive considerazioni sono del tutto indipendenti dal significato fisico dell'equazione di Schrödinger.

Lo spettro dell'operatore differenziale a primo membro della (11) è generalmente composto di due parti: il continuo, corrispondente a tutti i valori reali non negativi di k², e un eventuale numero finito di autovalori discreti, corrispondenti a valori negativi di k².

Allo spettro continuo si associano le due funzioni R(k) (‛coefficiente di riflessione') e T(k) (‛coefficiente di trasmissione'), definite univocamente mediante il comportamento della soluzione della (11) caratterizzato dalle relazioni asintotiche

(la seconda di queste due equazioni identifica la ψ(k, x) a meno di una costante moltiplicativa, che viene fissata dalla condizione che il coefficiente del primo termine a secondo membro della prima equazione sia esattamente l'unità; si ricordi che stiamo considerando il caso di k² > 0, cioè k reale).

Allo spettro discreto si associano le autofunzioni normalizzate (e reali) ψ(ip, x),

dove evidentemente k² = − pn² è l'autovalore (reale negativo). Queste autofunzioni definiscono le costanti (reali positive) ρ_n tramite la relazione asintotica

Si definisce ora trasformata spettrale della funzione u(x) l'insieme di dati

S : {R(k), − ∞ 〈 k 〈 + ∞; p_n, ρ_n, n = 1, 2, ..., N}, (15)

dove N indica il numero degli autovalori discreti, e per convenzione p_n > 0. Questa definizione è motivata dall'esistenza di una corrispondenza biunivoca fra la funzione u(x) e la sua trasformata spettrale S: in effetti è chiaro dalle equazioni già scritte che u(x) determina univocamente S tramite la soluzione del ‛problema spettrale diretto' caratterizzato dalle (11-14), laddove la determinazione (univoca) di u(x) da S equivale alla soluzione del ‛problema spettrale inverso e si effettua nel modo seguente. Data S, si costruisce la funzione

si considera quindi l'equazione di Gel′fand-Levitan-Marčenko (v. Calogero e Degasperis, 1982-1987, vol. I),

che determina univocamente la funzione K(x, x′) a partire dalla M(x) (la 17 è un'equazione di Fredholm per la dipendenza della K(x, x′) dalla seconda variabile x′; la dipendenza dalla prima variabile, x, è invece parametrica, dovuta all'esplicita presenza di questa variabile nella 17); infine, a partire dalla K(x, x′) si ottiene la u(x) dalla semplice formula

u(x) = − 2 dK(x, x)/dx. (18)

È importante osservare che vi è una diretta connessione fra la trasformata spettrale e la trasformata di Fourier. Infatti nel limite di campi deboli (se cioè la funzione u(x) è così piccola da permettere di trascurare ogni effetto non lineare, ivi compresa la presenza dello spettro discreto) le (16) e (17) implicano

sicché dalla (18) segue

û(k) ≈ ikR(k/2), (21)

dove û(k) è la trasformata di Fourier della u(x). Ecco dunque che la trasformata spettrale (che in questo limite si riduce alla funzione R(k)) si identifica essenzialmente (a meno di banali trasformazioni) con la trasformata di Fourier.

L'analogia della trasformata spettrale con la trasformata di Fourier può inoltre essere evidenziata dalle formule esatte

In queste formule ψ(k, x) e ψ(ip_n, x) sono le soluzioni della equazione di Schròdinger (11) caratterizzate dalle condizioni (12) e (13), laddove f(k, x) è la soluzione (detta ‛di Jost') della stessa equazione, caratterizzata dalla condizione asintotica

Queste equazioni evidenziano il carattere non lineare della trasformata spettrale, dovuto alla dipendenza delle autofunzioni ψ(k, x) e f(k, x) dalla u(x) (nello spirito del problema diretto) o dai parametri spettrali R(k), p_n e ρ_n (nello spirito del problema inverso). D'altronde è facile vedere che, se si trascurano tutti gli effetti non lineari (nonché ogni contributo dello spettro discreto), poiché in prima approssimazione (v. 11, 12 e 24)

ψ(k,x) ≈ exp(− ikx), f(k, x) ≈ exp(ikx), (25)

le (22) e (23) riproducono precisamente, usando la (21), le (4) e (3).

Questi risultati chiariscono in che senso la trasformata spettrale può essere considerata una generalizzazione non lineare della trasformata di Fourier, cui si riduce nel limite di ‛campi deboli', in cui vengano trascurati tutti gli effetti non lineari. Allo stesso modo il metodo di soluzione di equazioni non lineari di evoluzione mediante la trasformata spettrale (v. sotto) si ridurrà precisamente al metodo della trasformata di Fourier (v. cap. 2), nel limite di campi deboli, in cui ogni effetto non lineare venga trascurato (come vedremo, in tale limite la classe di equazioni non lineari risolubili mediante la trasformata spettrale si riduce precisamente alla sottoclasse delle equazioni (1) corrispondente al caso non dissipativo, in cui ω(z) nella (1) è un polinomio dispari).

Concludiamo questa parte osservando che i risultati qui descritti suggeriscono un ruolo speciale per quelle funzioni u(x) aventi trasformata spettrale particolarmente semplice. In particolare è possibile determinare esplicitamente la classe delle funzioni u(x) la cui trasformata spettrale contiene N autovalori discreti (caratterizzati dai 2N parametri p_n e ρ_n) e un coefficiente di riflessione identicamente nullo, R(k) = 0; infatti in tal caso l'equazione di Fredholm (17) si sa risolvere, essendo il nucleo M(x′′ + x′) separabile (di rango N). Particolarmente semplice (e, come vedremo, importante) è la funzione u(x) la cui trasformata spettrale contiene un solo autovalore discreto (caratterizzato dai parametri positivi p e ρ) e R(k) = 0:

u(x) = − 2p²/cosh²[p(x − ξ)], ξ = (2p)^-1 ln(ρ/2p). (26)

b) Relazione fra cambiamenti della funzione u(x) e cambiamenti della sua trasformata spettrale.

L'analogia con la tecnica di Fourier avrà già suggerito al lettore quale sia l'idea base del metodo di risoluzione di equazioni non lineari di evoluzione mediante la trasformata spettrale: identificare evoluzioni temporali della funzione u(x) (che diverrà dunque u(x, t)) tali che l'evoluzione temporale della corrispondente trasformata spettrale sia semplice. A tal fine occorre un formalismo che permetta di correlare dei cambiamenti della funzione u con i corrispondenti cambiamenti della trasformata spettrale. Uno strumento assai conveniente per effettuare tale analisi è fornito dalle seguenti relazioni:

In queste equazioni u₁(x) e u₂(x) sono due diverse funzioni, ψ₁(k, x) e ψ₂(k, x) le corrispondenti soluzioni del problema spettrale (11)-(12) e R₁(k), R₂(k) i corrispondenti coefficienti di riflessione; f(z) e g(z) sono due arbitrari polinomi, e infine Λ e Γ sono due operatori integro-differenziali, dipendenti da u₁(x) e u₂(x), e definiti dalle seguenti formule, che specificano la loro azione su due generiche funzioni F(x) e G(x) (F(x) deve ovviamente annullarsi per x → + ∞):

Queste equazioni implicano che, se due funzioni u₂(x) e u₁(x) sono legate da un'equazione del tipo

f(Λ)[u₂(x) − u₁(x)] + g(Λ)Γ • 1 = 0, (31)

i corrispondenti coefficienti di riflessione sono connessi dalla formula

f(−4k²)[R₂(k) − R₁(k)] + 2ikg(−4k²)[R₂(k) + R₁(k)] = 0 (32a)

ovvero

si osservi come una complicata relazione integro-differenziale non lineare fra u₁ e u₂, qual è la (31), si sia trasformata nella assai semplice relazione lineare (32).

Molti e notevoli risultati si possono ricavare dalle equazioni che abbiamo scritto (e dalle equazioni analoghe che si possono scrivere per i parametri di quella parte della trasformata spettrale che corrisponde allo spettro discreto); in questa sede occorrerà però limitarsi a considerarle nel caso più semplice, in cui la differenza fra u₂ e u₁ è infinitesima, e precisamente corrispondente a una (infinitesima) evoluzione temporale.

c) Evoluzione temporale; classe delle equazioni integrabili.

Consideriamo dunque una funzione u che dipenda anche da una seconda variabile t: u = u(x, t). Naturalmente la corrispondente trasformata spettrale, e in particolare il coefficiente di riflessione, dipenderà a sua volta da t: R = R(k, t). Poniamo ora, nelle equazioni (27)-(30) u₁(x) = u(x, t) e u₂(x) = u(x, t + dt) (e dunque anche R₁(k) = R(k, t), R₂(k) = R(k, t + dt)), ottenendo nel limite dt → 0 le formule

In queste equazioni f e g sono ancora due arbitrari polinomi (che potrebbero anche dipendere da t, sebbene, per semplicità, questo verrà escluso nel seguito), e l'operatore integro-differenziale L- è il limite di Λ (v. eqq. 29-30), per u₁(x) = u₂(x) = u(x, t), sicché la sua definizione esplicita è data dalla formula

che specifica l'azione dell'operatore integro-differenziale L- sulla generica funzione F(x) (annullantesi per x → + ∞).

Ponendo ora f = 1 (per semplicità) e g(z) = − a(z) nelle (33) e (34), e sommandole, si conclude immediatamente che, se la funzione u(x, t) soddisfa l'equazione di evoluzione

u_t(x, t) = α(L-) u_x(x, t), (36)

il corrispondente coefficiente di riflessione R(k, t) evolve secondo la semplice equazione

R_t(k, t) = 2ikα(−4k²)R(k, t), (37)

che può essere immediatamente integrata in modo esplicito:

R(k, t) = R₀(k) exp[2ikα(−4k²)t]; (38)

ovviamente la funzione R₀(k) è fissata dalle condizioni iniziali

R₀(k) = R(k, 0). (39)

La (36) è un'equazione non lineare di evoluzione per la funzione u(x, t); o, meglio, si tratta di una classe di tali equazioni, ciascuna delle quali corrisponde a una specifica scelta della funzione α(z). Nonostante la presenza dell'operatore integrale nella definizione (35) dell'operatore L-, è possibile dimostrare che la (33) è una pura equazione differenziale (purchè α(z) sia un polinomio, il che verrà sempre assunto nel seguito); infatti, qualunque potenza dell'operatore L-, applicata a u_x(x, t), produce solo una combinazione non lineare della u stessa e delle sue derivate (tutte le integrazioni si possono effettuare esattamente; si noti che questo implica che qualunque potenza di L-, applicata a u_x, produce in effetti una combinazione della u e delle sue derivate, avente la forma di un differenziale esatto, che risulta dunque automaticamente già predisposto per una integrazione esatta nel caso di ulteriore applicazione dell'operatore L-). In particolare

L- u_x = u_xxx − 6u_xu = (u_xx − 3u²)_x, (40)

L- ²u_x = (u_xxxx − 10u_xxu − 5ux² + 10u³)_x. (41)

Abbiamo dunque visto che all'evoluzione temporale descritta nello spazio delle configurazioni dall'equazione alle derivate parziali (36) per la u(x, t) corrisponde, nello spazio della variabile spettrale k, la semplice equazione (37) per il coefficiente di riflessione R(k, t), equazione che ammette la soluzione esplicita (38). Non meno semplice è l'evoluzione temporale della componente di spettro discreto della trasformata spettrale associata alla u(x, t), che può essere determinata in modo analogo, ed è data dalle formule esplicite

p_n(t) = p_n(0) = p_n, (42)

ρ_n(t) = ρ_n(0) exp[−2p_nα(4pn²)t]. (43)

Si noti, per inciso, che la prima di queste equazioni implica che, quando il campo u evolve nel tempo secondo la (36), gli autovalori dell'operatore lineare differenziale di Schrödinger − ∂²/∂x² + u(x, t) restano invariati: siamo dunque in presenza di una trasformazione isospettrale (questa osservazione svolge un ruolo fondamentale in altre formulazioni di questi stessi risultati).

In conclusione, se u(x, t) evolve secondo l'equazione non lineare alle derivate parziali (36), la corrispondente trasformata spettrale evolve in modo lineare e assai semplice, come specificato dalle formule esplicite (38)-(39) e (42)-(43). La soluzione del problema di Cauchy per la (36) (data la u(x, 0), calcolare la u(x, t)) si può dunque effettuare in 3 passi: 1) al tempo t = 0, passare dalla u(x, 0) alla sua trasformata spettrale (problema spettrale diretto); 2) lasciare evolvere la trasformata spettrale fino al tempo t, secondo quanto esplicitamente specificato dalle (38)-(39) e (42)-(43); 3) al tempo t, ritornare dalla trasformata spettrale alla funzione u(x, t) (problema spettrale inverso). L'analogia di questa procedura con quella, basata sulla trasformata di Fourier, applicabile a equazioni di evoluzione lineari (v. cap. 2) è del tutto evidente. È forse anche il caso di sottolineare che tanto il problema spettrale diretto che quello inverso comportano la soluzione di equazioni lineari: nel primo caso l'equazione di Schrödinger (11), nel secondo caso l'equazione di Gel′fand-Levitan-Marčenko (17).

La più semplice equazione non banale della classe corrisponde alla scelta a(z) = − z, e si scrive dunque

u_t(x, t) + u_xxx(x, t) − 6u_x(x, t)u(x, t) = 0; (44)

ecco per l'appunto l'equazione KdV (i fattori numerici di fronte ai diversi termini sono convenzionali: possono essere cambiati a piacere con dei banali cambiamenti di scala delle variabili indipendenti x e t o della variabile dipendente u). Le corrispondenti formule per l'evoluzione temporale della trasformata spettrale sono dunque in questo caso

R(k, t) = R(k, 0) exp[−(2ik)³t], (45)

ρ_n(t) = ρ_n(0) exp[(2p_n)³t]. (46)

5. Solitoni e solitroni

Nel capitolo precedente abbiamo identificato una classe di equazioni non lineari di evoluzione e abbiamo mostrato come queste equazioni possano essere risolte mediante la trasformata spettrale associata al problema di Schrödinger. Come nel caso della soluzione mediante trasformata di Fourier di equazioni di evoluzione lineari, il principale messaggio che si evince da questa analisi è che, per le equazioni di questa classe, l'evoluzione temporale è assai più semplice nello spazio delle variabili spettrali che nello spazio delle configurazioni. Pertanto, per comprendere il comportamento delle soluzioni di queste equazioni (e di conseguenza i fenomeni naturali schematizzati dalle equazioni stesse, quali che essi siano), occorre distinguere diverse componenti di ogni soluzione, rifacendosi alle proprietà del problema spettrale. Effettuiamo qui succintamente tale analisi, facendo prevalentemente riferimento, per semplicità, all'equazione KdV (9) (anche se evidentemente molte delle considerazioni che seguono valgono per l'intera classe (36), anzi per una classe anche più vasta: v. cap. 8).

La distinzione principale è fra la componente della trasformata spettrale associata allo spettro discreto e quella associata al continuo. Il contributo separato di queste due componenti è particolarmente evidente nella definizione (16) del nucleo M dell'equazione di Gel′fand-Levitan-Marčenko (17); naturalmente nella funzione u(x), ottenuta risolvendo tale equazione integrale e usando la (18), i due contributi risultano mescolati in modo non lineare, salvo quei casi - si veda più avanti - in cui essi sono sensibilmente diversi da zero solo in zone separate.

Consideriamo anzitutto il continuo; il contributo di questa componente alla u(x, t) viene generalmente chiamato ‛fondo' (background). Questa parte è presente anche se tutti gli effetti non lineari sono trascurabili, come avviene per esempio nell'approssimazione di campi deboli; in tal caso (si veda anche la trattazione dopo l'equazione (18)) il comportamento della soluzione corrisponderà a quello delle soluzioni dell'equazione lineare ottenuta trascurando tutte le parti non lineari: per esempio, nel caso dell'equazione KdV, tale equazione linearizzata si scrive

u_t(x, t) + u_xxx(x, t) = 0, (47)

ovvero

con

ω(k) = − k³; (49)

il comportamento delle sue soluzioni sarà al solito caratterizzato dal fenomeno della dispersione, regolato dalla (49), cui è associata la velocità di gruppo

v_g = ω′(k) = − 3k². (50)

Si noti che questa velocità è sempre negativa (o al più nulla); pertanto asintoticamente le soluzioni della (47), oltre a disperdersi (delocalizzandosi), tenderanno a sfuggire nel verso delle x negative. Più generalmente, come conseguenza della definizione (35) dell'operatore L-, nel limite in cui tutti gli effetti non lineari vengono trascurati, la classe (36) di equazioni non lineari si riduce precisamente alla classe (1) di equazioni lineari, con l'identificazione

ω(z) = − zα(− z²) (51)

(dunque, se α(y) è un polinomio in y di grado m, ω(z) è un polinomio ‛dispari' di grado 2m + 1). Perciò, per tutte le equazioni della classe (36) linearizzate (il che è giustificato quando la soluzione è localmente piccola ovunque), il comportamento qualitativo delle soluzioni è essenzialmente caratterizzato dal fenomeno della ‛dispersione' regolato dalla funzione di dispersione ω(k) definita dalla (51). Si noti la consistenza fra la validità del regime lineare nel caso di ‛campo debole' e il fatto che il fenomeno della dispersione assicura per l'appunto che l'evoluzione temporale causi un affievolimento locale del campo ovunque.

Si è discusso finora il comportamento delle soluzioni delle equazioni linearizzate; la motivazione di questa analisi, nel contesto delle equazioni non lineari, è che, grosso modo, la componente della soluzione corrispondente alla parte di spettro continuo della trasformata spettrale evolve come le soluzioni dell'equazione linearizzata; il suo comportamento è cioè qualitativamente caratterizzato dal fenomeno della dispersione: dunque questa parte della soluzione tenderà a delocalizzarsi e a viaggiare con la velocità di gruppo associata alla funzione di dispersione caratteristica dell'equazione di evoluzione linearizzata; per esempio nel caso della KdV la componente corrispondente al continuo tenderà, per la (50), ad allontanarsi asintoticamente nel verso delle x negative.

Gli effetti essenzialmente non lineari si manifestano invece nell'altra componente delle soluzioni delle equazioni non lineari di evoluzione che stiamo considerando, nella componente cioè che è associata alla parte di spettro discreto della trasformata spettrale e che, come ora vedremo, dà conto della comparsa dei solitoni.

Per analizzare il comportamento di questa componente cominciamo dal caso più semplice, quello cioè di una soluzione la cui trasformata spettrale sia caratterizzata dalla presenza di un solo autovalore discreto e da un coefficiente di riflessione nullo (si noti che le (38), (42) e (43) implicano che, se questa condizione è valida inizialmente, essa resta valida sempre). La forma esplicita della corrispondente soluzione nello spazio delle cotifigurazioni segue dalla (26) e dalle (42) e (43):

u(x, t) = − 2p²/cosh²{p[x − ξ(t)]}, (52)

con

ξ(t) = (2p)^-1 ln[ρ(t)/2p] = ξ₀ + vt,

ξ₀ = (2p)^-1 ln[ρ(0)/2p], (52a)

v = − α(4p²). (52b)

Questa soluzione descrive dunque un'onda localizzata che si muove, senza cambiare di forma, con la velocità v, data, in funzione del parametro p che caratterizza tanto l'altezza che la larghezza dell'onda, dalla formula (52b), in cui entra la funzione a caratterizzante la particolare equazione non lineare di evoluzione della classe (36). Ecco dunque il solitone!

Nel caso dell'equazione KdV che, come abbiamo visto, corrisponde ad α(z) = − z, l'espressione della velocità (52b) diventa

v = 4p²; (53)

dunque in questo caso il solitone si muove nel verso positivo dell'asse x con una velocità che è direttamente proporzionale alla sua altezza (ricordiamo ancora che questa è - a meno di una trasformazione galileiana a un sistema di riferimento in moto con velocità costante - proprio la rappresentazione analitica del fenomeno osservato da J. Scott Russell, la cui bella descrizione è riportata all'inizio dell'articolo; naturalmente in questo casò la funzione u(x, t) rappresenta il profilo della superficie dell'acqua nel canale, misurata in un sistema di riferimento diretto verso il basso).

Oltre alla soluzione solitonica testé descritta, possono darsi soluzioni multisolitoniche, la cui trasformata spettrale è ancora caratterizzata dall'annullarsi del coefficiente di riflessione, mentre la parte di spettro discreto contiene un numero finito, N, di autovalori, ciascuno dei quali dà origine a un diverso solitone. Nel caso dell'equazione KdV, tanto nel remoto passato che nel remoto futuro tale soluzione si riduce essenzialmente alla somma di N solitoni ben separati: nel remoto passato essi sono ordinati in modo che i più grandi sono più a sinistra; nel remoto futuro, viceversa, i più grandi, e perciò più veloci, si sono portati più a destra. L'unico effetto dello scavalcamento è l'aver determinato uno sfasamento (calcolabile in modo esplicito) rispetto alla posizione che ciascun solitone avrebbe avuto se non ne avesse scavalcati altri (o non fosse stato scavalcato da altri).

Nella fig. 2, A e B, si vede l'evoluzione temporale di due soluzioni a due solitoni dell'equazione KdV; i parametri dei solitoni sono scelti in modo che in un caso la collisione suggerisca l'interpretazione di una perdita di identità dei due solitoni durante la collisione, nell'altro piuttosto quella di uno scambio di identità.

Accenniamo infine, sempre facendo riferimento al caso dell'equazione KdV, al comportamento qualitativo di una soluzione generica, la cui trasformata spettrale conterrà dunque tanto un contributo di spettro continuo (coefficiente di riflessione R(k, t) non nullo) che di spettro discreto; l'entità di tali contributi è chiaramente fissata dalle condizioni iniziali (si osservi che solo la fase del coefficiente di riflessione varia nel tempo, laddove il suo modulo rimane costante, come anche costanti nel tempo sono gli autovalori discreti: v. eqq. (45) e (42)). Tale comportamento si ottiene combinando insieme quelli fin qui descritti. Dunque nel remoto futuro ogni soluzione si scomporrà in un certo numero di solitoni, che si allontanano nel verso positivo dell'asse x, e in un contributo di fondo, che tende a delocalizzarsi e ad andarsene in verso opposto; il numero e le proprietà dei solitoni sono determinati precisamente dalle caratteristiche della parte di spettro discreto della trasformata spettrale corrispondente alle condizioni iniziali.

Prima di concludere questo capitolo, è forse il caso di sottolineare che la classe di equazioni alle derivate parziali non lineari che posseggono soluzioni che viaggiano senza cambiare di forma è assai vasta. Si consideri per esempio la più generale equazione di evoluzione, nella forma

u_t = F[u, u_x, u_xx, ...], u = u(x, t); (54)

ebbene, è chiaro che essa ammetterà una soluzione del tipo

u(x, t) = f(x − vt), (55)

che descrive per l'appunto un'onda che trasla con velocità v, se l'equazione alle derivate ordinarie

vf ′ + F[f ′, f ′′, ...] = 0 (56)

ammette (magari solo per qualche opportuno valore di v) una soluzione f(y) che è regolare per ogni valore reale di y e che si annulla per y → ± ∞. Evidentemente questa non è una condizione molto restrittiva. Ma in generale ‛onde solitarie' di questo tipo, se collidono l'una con l'altra, daranno luogo a una fenomenologia assai più complicata che nel caso solitonico precedentemente descritto.

Per esempio la cosiddetta ‛equazione regolarizzata delle onde lunghe',

u_t + u_x − u_xxt − 6u_xu = 0, u = u(x, t), (57)

che è da certi punti di vista analoga all'equazione KdV scritta nella forma

u_t + u_x + u_xxx − 6u_xu = 0, u = u(x, t) (58)

(in effetti, le due equazioni coincidono nell'approssimazione u_t ≈ − u_x), ammette la soluzione

u(x, t) = A/cosh²[p(x − x₀ − vt)], (59)

con

A = A(p) = − 2p²/(1 − 4p²), (60a)

v = v(p) = 1/(1 − 4p²) (60b)

(si noti che la (59) è anche soluzione dell'equazione KdV (58), purché le (60) siano rimpiazzate dalle relazioni A = − 2p², v = 1 + 4p², che del resto coincidono approssimativamente con le (60) se il numero 4p² è sufficientemente piccolo). Ma non esistono soluzioni analiticamente note della (57) analoghe alle soluzioni multisolitoniche della (58) e, per un'opportuna scelta dei parametri p₁ e p₂, si può vedere (v. fig. 3) che la collisione di due soluzioni di tipo (59) della (57) dà luogo a una fenomenologia assai più complicata.

Alcuni puristi desidererebbero che il termine ‛solitone' fosse riservato esclusivamente a quegli oggetti che subiscono solo collisioni ‛elastiche', come, per esempio, quelli corrispondenti alle soluzioni delle equazioni della classe (36), e in particolare dell'equazione KdV; si ritiene, del resto, che tutte le equazioni non lineari di evoluzione che danno luogo a tale caratteristica fenomenologia solitonica siano anche integrabili mediante una qualche variante del metodo della trasformata spettrale. Questi puristi suggerirebbero di usare invece il termine ‛onda solitaria' oppure, forse meglio (v. Calogero e Degasperis, 1982-1987, vol. I), ‛solitrone' per identificare qualunque soluzione di un'equazione di evoluzione non lineare alle derivate parziali che abbia la caratteristica di mantenersi localizzata nel tempo e di comportarsi in sostanza come una particella (il termine ‛solitrone' è appunto proposto per la sua più diretta assonanza con i nomi delle particelle elementari: elettrone, positrone, ecc.). Secondo questa convenzione, tutti i solitoni sarebbero dunque solitroni; ma non viceversa, in quanto il termine ‛solitoni' resterebbe riservato a quei casi speciali nei quali queste soluzioni localizzate hanno la notevole proprietà di subire solo collisioni ‛elastiche'; dunque quei casi in cui le equazioni di evoluzione sono risolubili (esattamente linearizzabili) mediante la tecnica della trasformata spettrale o un metodo analogo. Occorre però avvertire che queste convenzioni sono largamente disattese, sicché frequentemente si usa, nei più svariati campi applicativi, il termine ‛solitone' per denotare qualunque ente esteso che in qualche modo si mantenga localizzato e abbia una qualche persistenza temporale.

6. Leggi di conservazione.

Le equazioni non lineari di evoluzione della classe (36) hanno molte altre notevoli proprietà, oltre quelle fin qui descritte. Ne ricorderemo qui solo una, ed è l'esistenza di un numero infinito di leggi di conservazione. Una formula compatta per esprimere queste quantità conservate (cioè indipendenti dal tempo) è

dove l'operatore integro-differenziale L- è quello definito dalla (35). Nonostante la presenza dell'operatore integrale in questa definizione di L-, e nonostante la presenza esplicita della variabile x nell'espressione su cui agisce l'operatore L- a secondo membro della (61), queste quantità conservate risultano tutte espresse come un singolo integrale su una combinazione della funzione u e delle sue derivate, senza che la variabile x compaia esplicitamente; per esempio, come è facile verificare con un calcolo esplicito a partire dalla (61),

7. Altre tecniche per lo studio di equazioni di evoluzione integrabili

Nei capitoli precedenti si è descritta in qualche dettaglio la tecnica della trasformata spettrale per la risoluzione della classe di equazioni non lineari di evoluzione (36); merito precipuo di questo approccio è quello di mettere in luce, tramite l'analogia con la trasformata di Fourier, il ruolo della scomposizione di una funzione u(x, t) nelle sue ‛componenti spettrali' (v. la 23) e, in tale ambito, il significato della componente solitonica.

È però importante sottolineare che vi sono numerose altre tecniche per lo studio di queste equazioni (nonché per l'analisi e l'identificazione di altre equazioni integrabili: v. cap. 8). Del resto, come la trasformata di Fourier, o più generalmente l'analisi armonica, influenza molti altri campi della matematica applicata e della matematica pura, oltre allo studio delle equazioni lineari di evoluzione alle derivate parziali, così la ‛rivoluzione solitonica' degli anni settanta ha investito molti altri campi della matematica applicata e pura, dalla topologia alla geometria differenziale e algebrica, allo studio dei sistemi hamiltoniani a un numero finito e infinito di gradi di libertà, alla teoria dei campi classici e quantistici, alle algebre di Lie e di Kac-Moody, all'analisi funzionale, ecc. Non è evidentemente possibile in questa sede dar conto di questi sviluppi e del resto non esiste al momento attuale una trattazione comprensiva di questa materia, che è ancora in fieri. Esistono però moltissimi articoli di ricerca, articoli di rassegna e libri; per una rassegna di questi lavori si rinvia, per esempio, al trattato di Calogero e Degasperis (v., 1982-1987).

8. Altre equazioni risolubili.

Come abbiamo già osservato nell'introduzione, se la tecnica della trasformata spettrale avesse permesso di risolvere solo l'equazione KdV, o solo l'intera classe di equazioni non lineari di evoluzione (36), la sua importanza sarebbe stata modesta. Ma, a partire dall'inizio degli anni settanta, si è visto che numerose altre equazioni non lineari di evoluzione, comprese alcune equazioni di grande interesse applicativo e teorico, sono risolubili esattamente con tecniche analoghe. Esempi di queste equazioni sono la cosiddetta ‛equazione non lineare di Schrödinger',

iu_t + u_xx + c ∣ u ∣² u = 0, u = u(x, t), (65)

la cosiddetta ‛equazione di seno-Gordon', che si presenta in due versioni,

la cosiddetta ‛equazione KdV modificata',

u_t + u_xxx − 6u_xu² = 0, u = u(x, t), (67)

e molte altre (una lista senza pretese di completezza, pubblicata nel 1982, elenca 37 equazioni risolubili, quasi tutte di notevole interesse applicativo o teorico: v. Calogero e Degasperis, 1982-1987, vol. I).

L'equazione non lineare di Schrödinger descrive l'evoluzione di un campo complesso ed è particolarmente importante dal punto di vista applicativo, essendo generalmente appropriata per descrivere l'evoluzione temporale di un'onda quasi monocromatica che si propaga in un mezzo debolmente lineare e dispersivo. Anche l'equazione di seno-Gordon è molto importante, sia per il suo interesse teorico (per esempio nella teoria delle superfici) sia come prototipo di equazione relativisticamente invariante, quindi particolarmente appropriata come equazione-modello per lo studio della teoria relativistica dei campi classici e quantistici, e pertanto della fisica teorica delle particelle elementari. Ma vi sono anche altre equazioni integrabili che presentano un particolare interesse per la fisica delle particelle elementari: per esempio le equazioni ridotte di Yang e Mills,

dove U- è una matrice di SU(n), det U- = 1, U- = U- (x, y, t).

La maggioranza delle equazioni non lineari di evoluzione, risolubili mediante il metodo della trasformata spettrale o tecniche analoghe, sono equazioni alle derivate parziali in due variabili, generalmente una spaziale e una temporale; ma vi sono anche esempi di equazioni in più variabili (per esempio le equazioni di Yang e Mills ridotte (68) contengono due variabili spaziali e una temporale), anche se l'estensione della tecnica della trasformata spettrale al caso di più variabili spaziali presenta ancora dei difficili problemi; è anzi dubbio che tale estensione possa risultare altrettanto fruttuosa e naturale quanto l'analoga estensione nel caso della trasformata di Fourier (è questo, attualmente, uno dei principali argomenti di ricerca).

Oltre alle equazioni alle derivate parziali, vi sono anche importanti esempi di equazioni integro-differenziali che sono risolubili con tecniche di questo tipo, nonché equazioni alle differenze finite, generalmente associate a una discretizzazione delle variabili spaziali e/o temporali, risolubili attraverso un opportuno adattamento della tecnica della trasformata spettrale o delle altre tecniche usate per la soluzione e lo studio delle equazioni alle derivate parziali.

Terminiamo questo capitolo ricordando la possibilità - ovviamente molto interessante dal punto di vista applicativo - di studiare anche equazioni che non sono esattamente risolubili mediante queste tecniche, partendo dalla soluzione di un'equazione integrabile che assomigli a quella che si vuol studiare e applicando tecniche perturbative. È chiaro che questo approccio può presentare degli importanti vantaggi rispetto alla tecnica più usuale, che consiste nello scegliere come punto di partenza per trattamenti di tipo perturbativo delle equazioni lineari (che fino a qualche anno fa erano essenzialmente le uniche a essere considerate risolubili esattamente); in questo modo si apre la prospettiva di tener conto in modo esatto, anziché perturbativo, di alcuni aspetti non lineari caratterizzanti la fenomenologia del sistema in studio. Occorre però sottolineare che lo sviluppo, in questo contesto, di tecniche perturbative efficienti e ben controllate è ancora lungi dall'esser stato realizzato; anche questo è, attualmente, uno dei principali campi di ricerca, insieme all'esplorazione di nuove famiglie di equazioni non lineari di evoluzione risolubili, per esempio quelle associate ad altre trasformate spettrali, basate cioè su nuovi problemi spettrali.

9. Applicazioni

Il nome di Fourier resta legato, nella storia della matematica, alla tecnica che porta il suo nome; eppure egli, scrivendo il suo famoso trattato, attribuiva assai maggior peso al contributo che esso portava alla comprensione del fenomeno della propagazione del calore - evidentemente di grande interesse applicativo - che all'introduzione di un artificio matematico per risolvere alcune delle equazioni originate dalla formulazione matematica di tale problema fisico. Ricordiamo questo episodio per sottolineare che l'importanza di una nuova tecnica matematica richiede una lunga prospettiva temporale per poter essere valutata appieno; sarebbe dunque da miopi attribuire troppa importanza alle applicazioni cui è associata la sua introduzione. Per questa ragione intendiamo limitarci in questa parte a un'esposizione stringata e succinta; anche perché l'altra alternativa richiederebbe una dettagliata trattazione di numerosi problemi in disparati campi, il che non è ovviamente possibile in questa sede.

È importante anzitutto chiarire in che senso la disponibilità di una tecnica matematica (quale quella precedentemente descritta) per l'esatta risoluzione di alcune equazioni non lineari di evoluzione contribuisca alla comprensione di quei fenomeni naturali che possono essere schematizzati - eventualmente in base ad appropriate approssimazioni - da tali equazioni. Infatti assai di rado è possibile utilizzare appieno le tecniche di risoluzione, cioè ottenere esplicitamente, in forma analitica, la soluzione che interessa; per esempio, anche nel caso delle equazioni di evoluzione lineari risolubili mediante la tecnica di Fourier, è raramente possibile effettuare esplicitamente le integrazioni associate alla trasformata di Fourier, diretta e inversa. Ma, come si è già indicato precedentemente, l'esistenza di una tecnica matematica di esatta risoluzione fornisce la chiave per la comprensione del comportamento qualitativo delle soluzioni, suggerisce cioè il linguaggio appropriato per capirne l'andamento. Grosso modo, sia per le equazioni lineari risolubili mediante la tecnica di Fourier sia per le equazioni non lineari risolubili utilizzando la trasformata spettrale, la regola generale è che l'evoluzione temporale è assai più semplice nello spazio delle k che nello spazio delle x. In termini fenomenologici, nel caso delle equazioni lineari risolubili mediante la tecnica di Fourier, ciò porta all'analisi del comportamento delle soluzioni - e dunque dei fenomeni naturali descritti da tali equazioni - in termini di dispersione, velocità di gruppo, ecc.; e inoltre suggerisce la metodologia più appropriata all'analisi sperimentale (per esempio, l'uso di radiazioni monocromatiche, corrispondenti a soluzioni aventi la più semplice struttura nello spazio delle k). In modo analogo, per tutti quei casi in cui l'evoluzione temporale è caratterizzata da equazioni non lineari risolubili mediante la trasformata spettrale, l'analisi fenomenologica andrà fatta anzitutto sulla base della presenza dei solitoni e del loro comportamento, del quale si darà, a seconda del particolare fenomeno naturale in considerazione, una specifica interpretazione fisica.

Nel precedente capitolo abbiamo accennato alla possibilità di risolvere, con il metodo della trasformata spettrale o mediante tecniche analoghe, numerose equazioni non lineari di evoluzione. La lista dei fenomeni che risultano, in appropriata approssimazione, riconducibili a queste equazioni è già assai vasta; è forse il caso di sottolineare a questo proposito che alcune delle equazioni succitate hanno, in qualche senso, un'importante caratterizzazione strutturale, che le fa emergere come naturale prima approssimazione (in cui si tiene però ancora conto dei principali effetti non lineari) per intere classi di equazioni non lineari di struttura più complessa (è questo il motivo matematico che giustifica la loro apparizione - specie per l'equazione KdV e l'equazione non lineare di Schrödinger - in un così gran numero di diversi contesti applicativi).

I campi di applicazione di queste tecniche sono dunque numerosi e in continua espansione: spaziano dall'idrodinamica all'ottica non lineare (fig. 4), dalla teoria della superfluidità alla fisica dei plasmi (fig. 5), dalla teoria delle reti elettriche alle generalizzazioni dei modelli alla Volterra di equilibrio ecologico, di dinamica delle popolazioni, di epidemiologia, alla cosmologia (le stesse equazioni della relatività generale di Einstein sono, in alcuni casi speciali ma non banali, risolubili con queste tecniche) (v. Calogero e Degasperis, 1982-1987).

Un discorso a parte richiedono le prospettive di utilizzazione di questi concetti nell'ambito della teoria delle particelle elementari, anche per sgombrare il campo da possibili equivoci. È chiaro che la scoperta di un meccanismo per cui, a partire da una teoria non lineare di campo, si generano entità localizzate - i solitoni - aventi caratteristiche di stabilità che permettono da molti punti di vista di identificarne il comportamento con quello di particelle, appare assai suggestiva. È importante osservare a questo proposito che ciò accade nell'ambito di teorie classiche, senza cioè che vi sia alcuna quantizzazione; sembra così realizzarsi la speranza di Einstein di poter trattare in modo naturale, senza bisogno della quantizzazione (con tutte le implicazioni filosofiche legate agli elementi non deterministici di tale teoria), particelle localizzate nell'ambito di una teoria non lineare di campo. D'altronde, anche nell'ambito di una teoria quantistica dei campi, ci si deve ben chiedere, nel caso esistano soluzioni di tipo solitonico delle corrispondenti equazioni classiche, se esse abbiano una controparte nella teoria quantizzata; fino a ipotizzare che esse diano luogo, anche nell'ambito di una teoria quantizzata, a una famiglia di particelle diversa da quelle che corrispondono ai quanti associati al campo mediante le usuali tecniche di quantizzazione.

Queste questioni sono invero assai interessanti, e ancora attendono risposta; ma occorre qui notare che, in questa problematica (che deve di necessità calarsi, per essere davvero realistica, nel contesto dello spazio tridimensionale, 0vvero dello spazio-tempo relativistico quadridimensionale), quello che gioca un ruolo essenziale è l'esistenza di soluzioni localizzate e, in qualche senso, stabili, delle equazioni classiche di campo, a prescindere dal fatto che queste corrispondano alla più stringente definizione di solitone (in quanto distinto da ‛solitrone') che abbiamo formulato sopra, e che è legata alla tecnica della trasformata spettrale (che del resto resta finora essenzialmente limitata, salvo qualche generalizzazione un poco artificiosa, a problemi ambientati in uno spazio unidimensionale). Dunque il gran parlare che si fa di solitoni nell'ambito della teoria delle particelle elementari si riferisce prevalentemente a qualcosa di diverso da quel che è stato discusso qui; e noi riteniamo che il futuro sviluppo della tecnica della trasformata spettrale (sarà esso davvero paragonabile per importanza a quello della trasformata di Fourier?) sia legato alle sue proprietà matematiche e alle sue applicazioni nella fisica matematica classica e nella matematica applicata, indipendentemente dal successo o meno delle idee solitoniche nell'ambito della teoria delle particelle elementari.

BIBLIOGRAFIA

Calogero, F., I solitoni, in Enciclopedia della scienza e della tecnica, Milano 1979.

Calogero, F., Degasperis, A., Spectral transform and solitons: tools to solve and investigate nonlinear evolution equations, 2 voll., Amsterdam 1982-1987.

Fermi, E., Pasta, J.R., Ulam, S.M., Studies of nonlinear problems, (1955), in Collected papers of Enrico Fermi, vol. II, rist., Chicago 1965, pp. 978 ss.

Fourier, J.-B., Théorie analytique de la chaleur, Paris 1822.

Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M., Method for solving the Korteweg-de Vries equation, in ‟Physical review letters", 1967, XIX, pp. 1095-1097.

Ikezi, H., Taylor, R.J., Baker, D.R., Formation and interaction of ion-acoustics solitons, in ‟Physical review letters", 1970, XXV, p. 11.

Korteweg, D.G., Vries, G. de, On the change of form of long waves advancing in a rectangular canal, and a new type of long stationary waves, in ‟Philosophical magazine", 1895, XXXIX, pp. 422-443.

Santarelli, A.R., Numerical analysis of the regularized longwave equation: anelastic collision of solitary waves, in ‟Nuovo Cimento", 1978, XLVI-B, pp. 179-188.

Scott, A.C., Chu, F.Y.F., McLaughlin, D.W., The soliton: a new concept in applied science, in ‟Procedings of the Institute of Electrical and Electronics Engineers", 1973, LXI, pp. 1443-1483.

Scott Russell, J., Report on waves, in Report of the fourteenth meeting of the British association for the advancement of science, London 1945, pp. 331-390.

Slusher, R.E., Gibbs, H.M., Self-induced transparency in atomic rubidium, in ‟Physical review", 1972, V-A, p. 1634.

Zabusky, N.J., Kruskal, M.D., Interaction of ‛solitons' in a collisionless plasma and the recurrence of initial states, in ‟Physical review letteres", 1965, XV, pp. 240-243.