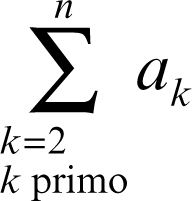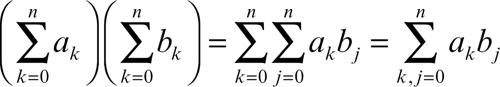sommatoria
sommatoria
sommatoria addizione di un numero finito o di un’infinità numerabile di termini, elencabili attraverso un indice. Se gli addendi sono in numero finito e sono indicizzati come a1, a2, ..., an, si scrive allora
(che si legge «sommatoria di ai, per i variabile da 1 a n»), utilizzando l’apposito simbolo di sommatoria. Questa scrittura abbreviata, caratterizzata dalla lettera sigma maiuscola e dall’indicazione sopra e sotto di essa della variabilità di uno o più indici interi, equivale alla scrittura estesa a1 + a2 + … + an e indica l’addizione degli n termini che si ottengono dal termine generale ai dando successivamente a i tutti i valori che vanno da 1 a n: l’indice i può essere equivalentemente contrassegnato con un qualsiasi altro simbolo formale senza alterare il senso della notazione (variabile muta). Spesso si usano varianti del simbolo di sommatoria, come
o, quando non vi siano ambiguità,
o, più semplicemente ancora,
Nel caso di più indici interi, per esempio,
il simbolo indica la somma di tutti i possibili addendi del tipo akbj al variare sia dell’indice k sia dell’indice j, indipendentemente l’uno dall’altro, da 0 al valore n. Convenzionalmente
Mentre l’indice di sommatoria è una variabile muta, nel senso che può essere sostituito da un’altra lettera senza alterare il valore della sommatoria, il primo e il secondo estremo della sommatoria sono essenziali. Essi possono essere assegnati (come nei precedenti esempi i valori 1 o 0) o variabili (come n); in tal caso la sommatoria è funzione delle variabili da cui dipendono gli estremi variabili. Per esempio,
dipende da m e da n. Se il secondo estremo è infinito si parla di → serie. A volte si aggiungono condizioni sull’indice: per esempio
indica che la somma va estesa solo ai valori primi dell’indice compresi tra 2 e n.
Proprietà della sommatoria
Poiché le sommatorie sono somme, valgono per esse tutte le proprietà dell’addizione, per esempio, applicando la proprietà commutativa e la proprietà associativa, si avrà:
Invece per il prodotto si avrà:
(l’ultima espressione è una forma sintetica della seconda). Ne consegue che per il simbolo di sommatoria vale la proprietà di linearità: