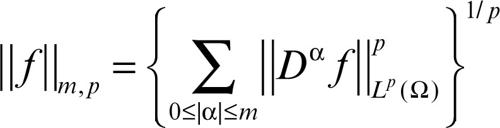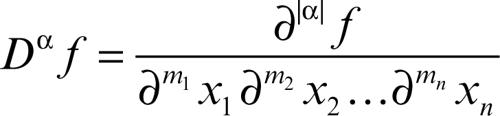Sobolev, spazi di

Sobolev, spazi di

Sobolev, spazi di spazi W^m,p(Ω), con m ∈ N, p ∈ [1, ∞], Ω ⊂ Rⁿ, costituiti dalle funzioni appartenenti a → spazi L^p(Ω) dotati di derivate (nel senso delle → distribuzioni) di ogni ordine α, con |α| ≤ m, che siano a loro volta funzioni appartenenti a L^p(Ω). Essi sono spazi di → Banach con la norma

per p < ∞,

dove la derivata D^αƒ, corrispondente al multiindice α = (m₁, m₂, …, m_n) di lunghezza

è

Numerosi teoremi (detti di immersione e dovuti a S.L. Sobolev e al matematico americano Ch.B. Morrey) stabiliscono relazioni di immersione, dipendenti dai parametri m, n, p, q, k, tra W^m+j,p(Ω) e W ^j,q(Ω^k), o la continuità di ƒ e delle sue derivate, essendo Ω^k una sezione k-dimensionale di Ω. Analoghi teoremi (dovuti principalmente al matematico tedesco F. Rellich, come il cosiddetto teorema di Rellich-Kondrachov) legano W^m+j,p(Ω) e W ^j,q(Ω₀^k), dove Ω₀ è un sottoinsieme di Ω, specificando quando l’immersione è compatta, cioè quando una successione limitata nel primo spazio è convergente (a meno di estrarre sottosuccessioni) nel secondo. Sono stati introdotti, per le applicazioni alle equazioni differenziali alle derivate parziali, anche spazi di interpolazione corrispondenti a valori non interi di m.