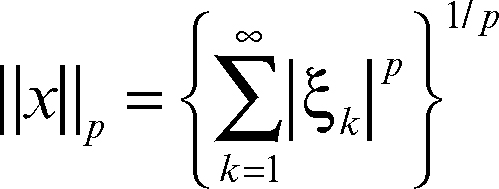spazio l p

spazio l p

spazio l ^p spazio vettoriale delle successioni x = {ξ_k} per cui la serie

è convergente. Se p ≥ 1, lo spazio è normato, con norma

e completo in tale norma; è quindi uno spazio di → Banach. Se p ∈ (0, 1), lo spazio è ancora vettoriale, ma non è normato. Lo spazio l ^∞ costituito dalle successioni limitate è di Banach con norma

Se 1 ≤ p ≤ q ≤ ∞, risulta l ^p ⊂ l ^q, con immersione continua. Se p e p′ soddisfano l’uguaglianza

essi si dicono esponenti coniugati; per p < ∞, il duale di l ^p è l ^p′ e quindi, se 1 < p < ∞, gli spazi l ^p sono riflessivi. Se y = {η_k} ∈ l ^p′, risulta

(→ Hölder, disuguaglianza di). In particolare, lo spazio l ² è uno spazio di → Hilbert.