Archimede, spirale di
Archimede, spirale di
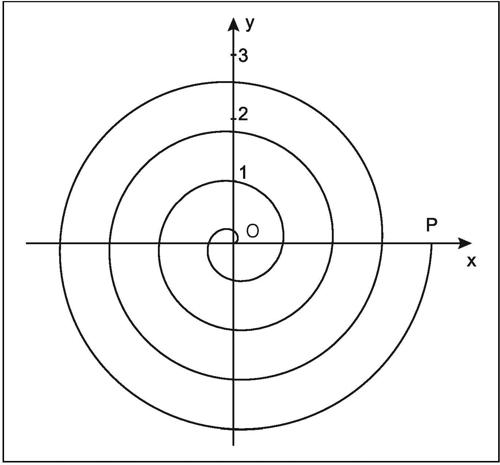
Archimede, spirale di curva piana aperta che si ottiene componendo il moto uniforme di un punto P su una semiretta avente come origine un punto O con la rotazione uniforme della semiretta stessa nel piano attorno al suo estremo. La distanza ρ di P da O è ogni volta direttamente proporzionale all’ampiezza θ dell’angolo di cui è ruotata la semiretta; in coordinate polari, l’equazione della spirale di Archimede è perciò
dove l’ampiezza θ è espressa in radianti e k è una costante non nulla. In figura è rappresentato l’arco di spirale di equazione
e si nota come il punto P della spirale sia a distanza π dall’origine proprio al compimento della quarta spira (θ = 4 · 2π).
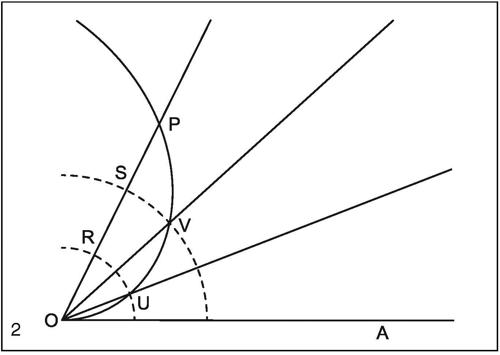
La spirale di Archimede è legata a due classici problemi di costruzione: quello della divisione di un angolo in tre parti uguali (→ angolo, trisezione di un) e quello della → quadratura del cerchio. Per dividere un angolo AÔP in tre parti uguali, si considera l’arco di spirale che va da O a P; si divide quindi in tre parti uguali (OR, RS e SP) il segmento OP (→ costruzione con riga e compasso) e, con il compasso, si tracciano gli archi di circonferenza di raggi OR e OS che intersecano rispettivamente la spirale nei punti U e V. Le semirette OU e OV dividono l’angolo dato in tre parti uguali.
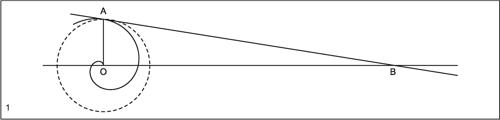
Per il problema della quadratura del cerchio, che consiste nel tracciare un segmento rettilineo di lunghezza uguale a una circonferenza data, Archimede considera due assi perpendicolari per O, l’arco di spirale OA che si ottiene con un giro completo (0 ≤ θ ≤ 2π), e la tangente alla spirale nel punto A: tale tangente interseca l’asse orizzontale nel punto B e il segmento OB ha lunghezza uguale alla circonferenza di raggio OA.