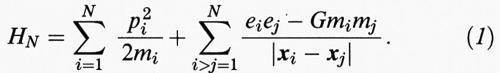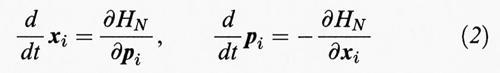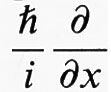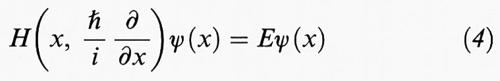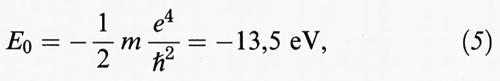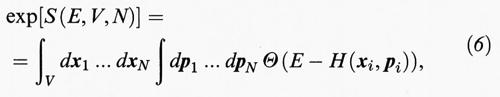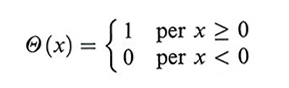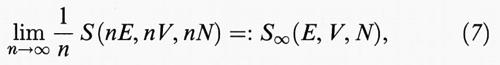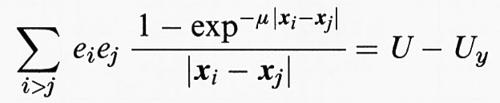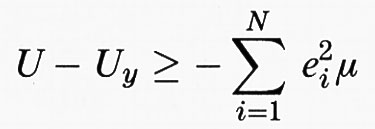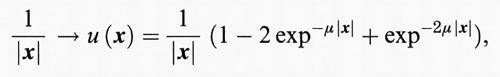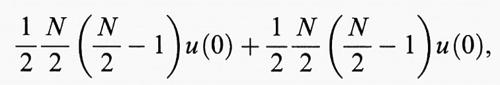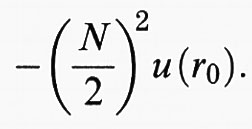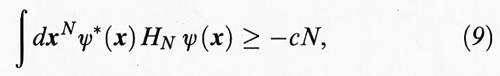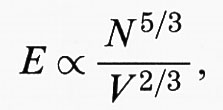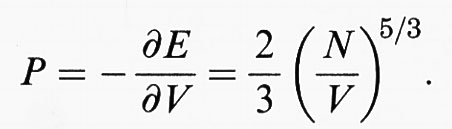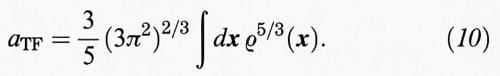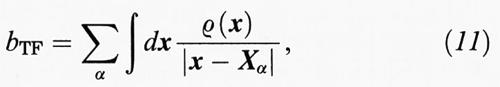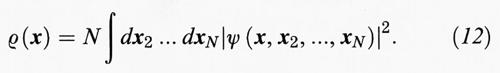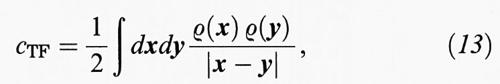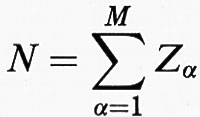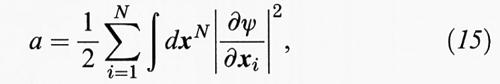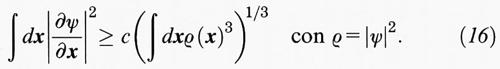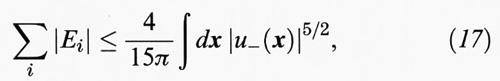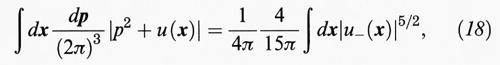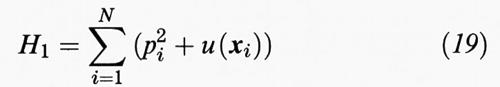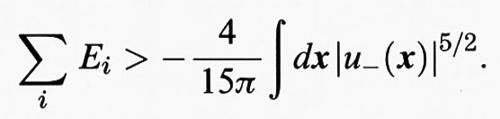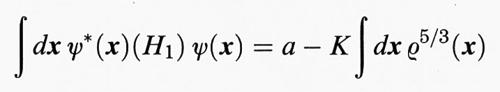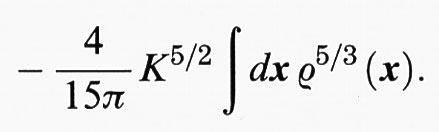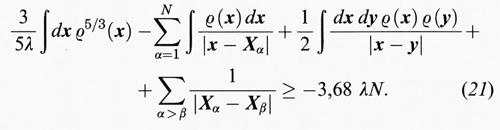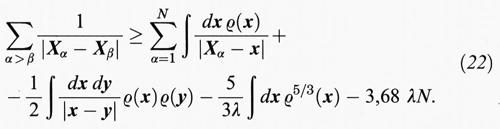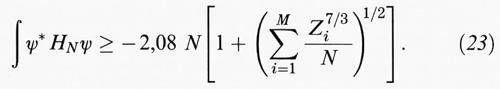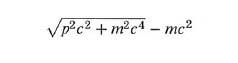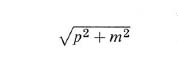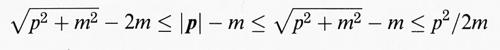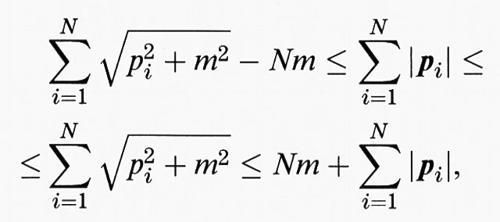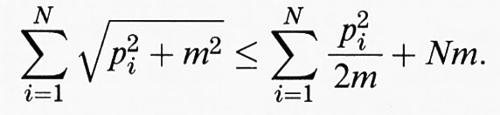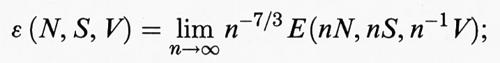Materia, stabilita della

Materia, stabilità della

sommario: 1. Introduzione storica. 2. Argomenti euristici. 3. La dimostrazione. 4. Conseguenze. a) Stabilità relativistica. b) L'esistenza di dinamiche locali. c) Stabilità termodinamica. □ Bibliografia.

1. Introduzione storica

Nel XX secolo si è avverato un antico sogno degli scienziati. Dai tempi di Democrito fino a Boltzmann è esistita la convinzione che le leggi che governano la materia che ci circonda discendessero da quelle più fondamentali che regolano il comportamento degli elementi costituenti la materia stessa, cioè gli atomi. Si deve a Ernest Rutherford la scoperta, avvenuta in questo secolo, della struttura degli atomi che, secondo il suo modello, risultano costituiti da elettroni con carica negativa che ruotano a una distanza di circa 10^-8 cm intorno a un nucleo positivo estremamente piccolo, circa 10^-12-10^-13 cm. Rutherford scoprì anche che la forza di Coulomb F = x e₁e₂/∣x∣³ tra due cariche e₁ ed e₂ aventi la posizione relativa x (∣x∣ denota la lunghezza del vettore x), è valida anche a queste piccole dimensioni e che non vi è alcun segno che esistano altre forze se non quelle che agiscono nel nucleo. Per la prima volta si ebbe la possibilità di dedurre le proprietà degli atomi e anche di corpi di dimensione maggiore dalle leggi della meccanica, che a quel tempo erano quelle della meccanica hamiltoniana: secondo tali leggi le equazioni del moto discendono dall'energia H (x_i, p_i) come funzione della posizione x_i e della quantità di moto p_i della particella i-esima (i = 1, 2, ..., N, dove N è il numero totale delle particelle). Tale energia è composta dall'energia cinetica - che vale p²/2m per una particella di massa m - e dall'energia potenziale che, nel caso di interazione elettrostatica fra due cariche e₁ ed e₂ a distanza relativa ∣x∣, è uguale a e₁e₂/∣x∣. La forza è uguale al gradiente dell'energia potenziale cambiato di segno - il che corrisponde esattamente alla forza di Coulomb menzionata in precedenza - ed è attrattiva per cariche di segno opposto, e₁e₂ 〈 0, e repulsiva se e₁e₂ > 0. Questa forza ha la stessa forma algebrica della forza gravitazionale di Newton tra due masse m₁ e m₂, ma questa è sempre attrattiva e ha pertanto un'energia potenziale - Gm₁m₂/∣x∣, dove G è la costante gravitazionale. All'inizio del secolo erano note solo queste due forze e la forza magnetica, che si pensava avesse un'importanza minore. Poiché queste energie sono additive, l'energia totale (‛hamiltoniana') di N particelle cariche che interagiscono elettrostaticamente e gravitazionalmente equivale esattamente alla somma delle singole energie

Secondo le regole della meccanica hamiltoniana, l'evoluzione temporale del sistema è determinata dalle equazioni del moto

(t rappresenta il tempo), e perciò il comportamento di un simile sistema può in teoria essere previsto. Purtroppo (o per fortuna) questa teoria non ebbe successo per due ragioni. Le equazioni risultanti possono essere risolte facilmente per N = 2, ad esempio nel caso di un protone e di un elettrone che costituiscono l'atomo di idrogeno. La soluzione era già stata trovata da Newton quando spiegò il moto dei pianeti intorno al Sole che possono descrivere orbite ellittiche di qualsiasi diametro, ma in questa equazione non c'è nulla che spieghi perché un atomo di idrogeno debba sempre avere una dimensione di circa 10^-8 cm. La seconda obiezione deriva dal fatto che l'equazione non tiene conto di un fenomeno, già noto a quel tempo, consistente in un accoppiamento fra sistema atomico e campo elettromagnetico per cui quest'ultimo può sottrarre energia al sistema. Questa cosiddetta radiazione elettromagnetica si manifesta quando le cariche sono accelerate, come accade nel caso delle orbite ellittiche menzionate sopra. Pertanto l'elettrone, ruotando intorno al protone nell'atomo di idrogeno, dovrebbe continuamente perdere energia per effetto della radiazione elettromagnetica, e ciò potrebbe avvenire solo a spese della sua energia potenziale che determinerebbe un suo progressivo avvicinamento al nucleo. L'elettrone finirebbe così per cadere sul nucleo e il raggio dell'atomo si ridurrebbe a zero. Poiché tale catastrofe non si manifesta in natura, apparve evidente che le leggi conosciute all'inizio del secolo non potevano applicarsi alla scala atomica. Il primo passo verso la spiegazione di questo misterioso raggio minimo di 10^-8 cm fu fatto da Niels Bohr, il quale postulò che il momento della quantità di moto dell'elettrone rispetto al nucleo corrispondesse a un numero intero moltiplicato per il quanto di azione ℏ di Planck (ℏ = h/2π, in cui h è la costante di Planck); si ottiene in tal modo che solo orbite con raggi particolari sono possibili e il più piccolo dei raggi possibili è il famoso ‛raggio di Bohr', a₀ = ℏ²/m e² = 0,51 • 10^-8 cm, che corrisponde a un momento della quantità di moto pari a ℏ. La meccanica quantistica di Bohr non era una teoria completa, ma un insieme di regole per casi particolari: si dovettero attendere oltre dieci anni prima che W. K. Heisenberg ed E. Schrödinger riuscissero a trovare una teoria generale. Heisenberg postulò che x e p dovessero essere considerati non come numeri ma come elementi di un'algebra non commutativa e cioè tali da soddisfare la regola

x p - px = i ℏ (3)

(i è l'unità immaginaria).

Schrödinger spiegò l'equazione (3) interpretando p come l'operatore differenziale

e postulò che i valori permessi dell'energia E fossero quelli per i quali l'equazione

ha una soluzione tale che la ‛funzione d'onda' ψ (x) è una funzione a quadrato sommabile ∫ dx ∣ψ (x)∣² 〈 ∞. Questa condizione fissò l'energia minima di un atomo d'idrogeno

che corrisponde esattamente all'energia di ionizzazione dell'idrogeno. Inoltre, la ψ corrispondente è concentrata intorno al protone entro una distanza a₀; ciò suggerì a Max Born di interpretare ∣ψ (x)∣² come la probabilità di trovare l'elettrone nel punto x. Inoltre, Schrödinger riuscì a dedurre matematicamente dall'equazione (3) che le incertezze Δx e Δp di x e p per una tale distribuzione di probabilità soddisfano la relazione di indeterminazione

come era stato già trovato con considerazioni euristiche da W. K. Heisenberg. La (5a) rende plausibile il fatto che l'elettrone non cada sul nucleo. Infatti, poiché il valore medio di p² è sempre maggiore di (Δp)², l'energia cinetica p²/2m è maggiore di ℏ²/8m (Δx)² e, se il valore medio di 1/∣x∣ è dell'ordine di 1/Δx, ne segue che l'energia è maggiore di h²/8m (Δx)² - e²/Δx. Se calcoliamo il minimo rispetto a Δx, otteniamo (a meno di un fattore 4) E₀ per Δx ≅ a₀ (lo ‛stato fondamentale'). Ciò spiega perché l'elettrone non cada nel nucleo; in seguito, lo sviluppo della teoria quantistica del campo elettromagnetico chiarì anche come mai l'elettrone nello stato fondamentale non irradi: infatti esso non ha energia da spendere.

Una volta compreso il comportamento dell'atomo di idrogeno fu possibile concentrarsi su strutture più grandi, come gli atomi più pesanti, le molecole o addirittura la materia macroscopica. Si scoprì così un'altra caratteristica dell'elettrone, cioè il fatto che esso soddisfa la statistica di Fermi. Secondo la meccanica quantistica, lo spazio delle fasi (lo spazio di x e p) acquista una struttura discreta in cui la cella elementare ha un volume Δx • Δp ~ ℏ. Le particelle che obbediscono alla statistica di Fermi (i cosiddetti fermioni, cioè elettroni, protoni e neutroni) non ‛vogliono' condividere tali celle con altre particelle dello stesso tipo, diversamente dall'altro tipo di particelle (cioè i bosoni, come i fotoni o le particelle α). Questa idea euristica è espressa dalla condizione che la funzione d'onda ψ deve cambiare segno quando si scambiano le coordinate di due fermioni identici. Poiché per un'energia cinetica data l'impulso p è dell'ordine di ~ √−m e perciò Δx ~ 1/√−m, sono i fermioni più leggeri, cioè gli elettroni, a risentire maggiormente della granularità dello spazio delle fasi (e della statistica di Fermi). Proprio grazie alla statistica di Fermi fu possibile spiegare strutture più complesse e addirittura la struttura di certi corpi macroscopici, come fece Sommerfeld con la teoria elettronica dei metalli. Sembrò quasi possibile realizzare il sogno di Boltzmann e dedurre le proprietà dei corpi dall'equazione di Schrödinger (4) utilizzando l'espressione (1) per H; si scoprì però che restava da percorrere ancora una lunga strada.

Le leggi della termodinamica, che sono state dedotte fenomenologicamente nel secolo scorso, valendo indipendentemente dalla loro forma, dimensione e composizione chimica dei corpi macroscopici, mostrano una certa universalità nel comportamento di tali corpi. Ci si aspetta che queste proprietà discendano dalle leggi microscopiche nel cosiddetto limite termodinamico, cioè quando il numero delle particelle N → ∞. L'esistenza di tale limite non è assolutamente banale, ma presuppone che tutti i sistemi macroscopici abbiano delle caratteristiche comuni nonostante la complessa natura delle dinamiche microscopiche. Ciò che dovrebbe tendere a un limite finito nel limite termodinamico, N → ∞, è l'energia per particella E/N, la densità di particelle N/V (dove V rappresenta il volume nel quale sono confinate le particelle), e la densità di entropia S/V. L'entropia è definita classicamente da

dove Θ è la funzione gradino

e l'integrale è esteso allo spazio 6N-dimensionale (‛spazio delle fasi') con coordinate x₁, ..., x_N, p₁, ..., p_N. In realtà, se H è data dall'espressione (1), l'integrale è infinito poiché l'energia potenziale può arrivare a - ∞; nella teoria quantistica, invece, l'espressione corrispondente, che rappresenta il numero dei valori permessi di energia inferiore a E, è finita. Perciò l'esistenza del limite termodinamico richiede che esista il limite

il che matematicamente significa che, per grandi valori degli argomenti, S diventa una funzione omogenea di grado 1 dei suoi argomenti. Inoltre, il sistema deve essere termodinamicamente stabile, e ciò richiede che il calore specifico e la compressibilità devono essere maggiori di zero. Perché queste quantità, legate alle derivate seconde di S, risultino di segno positivo occorre che la funzione E_∞ (S, V, N), definita implicitamente dall'equazione (6), sia convessa (cioè curva verso l'alto) nei suoi argomenti. Questa proprietà è legata all'omogeneità dal seguente teorema.

Sia F (x) una funzione R^d → R tale che F (0) = 0. Allora, ciascuna coppia delle tre proprietà:

O (omogeneità): F (lx) = lF (x) ∀ l ∈ R⁺,

C (convessità): F (lx₁ + (1 - l) x₂) ≤ lF (x₁) + (1 - l) F (x₂) ∀ 0 ≤ l ≤ 1,

S (subadditività): F (x₁ + x₂) ≤ F (x₁) + F (x₂),

implica la terza. Se ora poniamo in particolare d = 3, F = E_∞ (S, V, N) (che soddisfa F (0) = 0), le tre proprietà acquistano il seguente significato fisico.

(O): questo requisito è equivalente all'esistenza del limite nell'equazione (7) e significa che nello stato di equilibrio l'energia per particella tende a un limite (‛estensività' di E, V e S). Tradotto in linguaggio comune, ciò vuol dire che l'energia contenuta in due litri di benzina è il doppio di quella contenuta in un litro. Se questa proprietà non fosse soddisfatta, il sistema guadagnerebbe energia collassando; in altre parole, (O) rappresenta la stabilità contro l'implosione.

(C): significa che il valore di F per un valore di x compreso tra x₁ e x₂ è inferiore alla media dei valori di F calcolati in x₁ e x₂. Ne consegue che la funzione F è curva verso l'alto e perciò ha derivate seconde positive. Poiché queste sono legate al calore specifico e alla compressibilità, (C) è equivalente alla stabilità termodinamica.

(S): significa che E_∞ (S₁, N₁, V₁) + E_∞ (S₂, N₂, V₂) ≥ E_∞ (S₁+S₂, N₁+N₂, V₁+V₂); perciò si ottiene un guadagno di energia combinando due sistemi che abbiano, rispettivamente, N₁ e N₂ particelle. Quindi S rappresenta una condizione di stabilità contro l'esplosione. Ciò evidentemente è vero se si ha solo attrazione, come nel caso della gravitazione, mentre non si manifesta nel caso della sola repulsione, come nel caso di cariche elettriche di segno uguale. Non è detto che questa proprietà valga anche nel caso di repulsione e attrazione, come nei sistemi elettricamente neutri. In meccanica quantistica i sistemi neutri si attraggono per effetto della cosiddetta forza di van der Waals (v. Lieb e Thirring, 1986) e perciò in questo caso la condizione (S) è soddisfatta.

In base al teorema sopra enunciato, una coppia qualunque di queste condizioni di stabilità implica la terza o, inversamente, quando una è violata le altre due non possono essere entrambe soddisfatte. In termodinamica sono necessarie tutte e tre queste condizioni e si dava per scontato che si verificassero. Nel 1965, M. Fisher e D. Ruelle (v., 1966) sottolinearono per la prima volta che per la materia reale, dominata dalle forze coulombiane, non esisteva una dimostrazione della validità delle tre condizioni e perciò l'intero edificio della termodinamica mancava di fondamenta.

La prima dimostrazione dell'omogeneità per lo stato fondamentale della materia reale (in assenza di gravità) fu data da F. J. Dyson e A. Lenard (v., 1967) con un procedimento molto complesso. Come vedremo fra poco, il fatto che valga l'omogeneità è un'eccezione piuttosto che la regola, e una dimostrazione di ciò non poteva che essere matematicamente complessa visto che era necessario prendere in considerazione circostanze speciali. E. H. Lieb e W. Thirring (v., 1975) dimostrarono in seguito che la brillante intuizione fisica di Thomas e Fermi aveva aperto la strada per una dimostrazione molto più semplice dell'omogeneità.

Nel 1969, J. L. Lebowitz e Lieb (v., 1969) dimostrarono anche la subadditività e quindi, in base al teorema enunciato sopra, tutte e tre le condizioni di stabilità venivano a essere soddisfatte per la materia costituita da elettroni e nuclei. Il sogno di Boltzmann - riuscire a dedurre in maniera inequivocabile le leggi della termodinamica dalle leggi della dinamica microscopica che ne sono il fondamento - si era dunque realizzato.

2. Argomenti euristici

Per dimostrare (O) per lo stato fondamentale, bisogna dimostrare che il valore più basso di E per una soluzione a quadrato sommabile dell'equazione

Hψ = Eψ

antisimmetrica nelle coordinate dell'elettrone, è limitato inferiormente da E > - ε₀N, dove l'energia per particella ε₀ è indipendente da N. Poiché ogni grammo di materia contiene circa N = 10²⁴ elettroni, neppure il più potente calcolatore può risolvere questo problema che sembra perciò tanto al di fuori della nostra portata quanto raggiungere le stelle. Nonostante queste difficoltà il problema è stato risolto; tuttavia, prima di illustrarne la soluzione matematica, è utile introdurre alcune argomentazioni di carattere intuitivo che, pur non rappresentando una vera dimostrazione, possono indicare la direzione in cui ricercare la soluzione.

D'ora in poi ci interesseremo solo alla dipendenza da N dei vari contributi all'energia in (1) e abbandoneremo le costanti ℏ e 2m usando unità in cui esse valgono 1; inoltre, talvolta scriveremo α per e o per Gm², poiché considereremo separatamente i contributi coulombiano e gravitazionale.

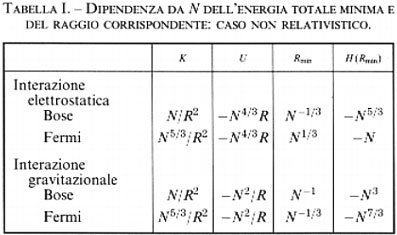
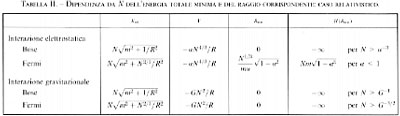
Come abbiamo detto, l'energia cinetica p²/2m è maggiore di 1/(Δx)², dove Δx rappresenta lo spazio disponibile per la particella. Se abbiamo N particelle in un volume V = R³, il valore di Δx dipende in maniera critica dal carattere bosonico o fermionico delle particelle. I bosoni possono condividere il volume con altre particelle e dunque possiamo porre Δx = R. I fermioni, al contrario, non possono occupare la stessa posizione e perciò dobbiamo dividere il volume in N celle, una per ciascun fermione. Ciascuna cella ha la dimensione (V/N)^1/3= RN^-1/3, che rappresenta il valore di Δx da usare per i fermioni. Di conseguenza, per tutte le N particelle abbiamo un'energia cinetica K = N/R² nel caso dei bosoni, e K = N^5/3/R² nel caso dei fermioni. Per valutare l'energia potenziale dobbiamo distinguere tra il caso in cui domina l'energia gravitazionale e il caso in cui è l'energia elettrostatica a dominare. Nel primo, ogni coppia di particelle dà un contributo - α/R, e poiché ci sono N (N - 1)/2 coppie, l'energia potenziale sarà dell'ordine di U = - αN²/R. Nel caso elettrostatico in cui si ha lo stesso numero di cariche negative e positive, l'interazione sarà schermata a grandi distanze; solo le particelle vicine saranno effettivamente in interazione e si disporranno in modo da avere cariche di segno opposto. Poiché la distanza dalla particella più vicina sarà di R/N^1/3 (il valore di Δx per i fermioni), l'energia potenziale per una particella è - ∝ N^1/3/R, e perciò per N particelle l'energia elettrostatica sarà dell'ordine di U = - αN^4/3/R. Nello stato di energia più bassa il sistema occuperà un volume di raggio R in modo da minimizzare l'energia totale H = K + U. La tab. I mostra quale sia nei diversi casi la dipendenza da N del raggio R_min che minimizza l'energia e l'energia corrispondente H (R_min). Come si vede dalla tabella, l'andamento H (R_min) ∝ - N, necessario per la stabilità, si verifica solo una volta nei quattro casi riportati, e cioè nel caso dei fermioni con interazioni elettrostatiche. In tutti gli altri casi, l'energia tende a - ∞ con una potenza di N maggiore di 1 e inoltre R_min decresce al crescere di N; perciò il volume del sistema tende a diminuire e la densità delle particelle N/R³ tende a ∞ per N → ∞. Solo nel secondo caso otteniamo R ∝ N^1/3, in modo che la densità rimane costante per N →∞. È per questo motivo che abbiamo chiamato l'andamento H ∝ - N stabilità contro l'implosione.

Molti dei risultati di queste semplici considerazioni potrebbero essere dimostrati da un'analisi matematica esatta (v. Lieb, 1991); tali risultati sono però inconcludenti per i seguenti motivi.

Per ciò che riguarda l'energia cinetica K, per ottenere un'attrazione netta nel caso elettrostatico ci deve essere una correlazione tra cariche positive e negative con una lunghezza di correlazione proporzionale a RN^-1/3. Ciò richiede un'ulteriore energia cinetica che, per quanto nel caso dei fermioni non possa competere con quella già considerata, può farlo nel caso dei bosoni. Un'analisi esatta dimostra che se i bosoni con carica di un solo segno hanno una massa infinita (e perciò nessuna energia cinetica), la stima precedente è corretta. D'altro canto, se tutte le masse sono finite l'aumento dell'energia cinetica fa sì che H, invece che comportarsi come - N^5/3, va come - N^7/5, ma il sistema non è ancora stabile.

Quanto all'energia potenziale U, in tutte le nostre stime abbiamo usato un potenziale a lunga portata 1/∣x∣, ma ciò che è importante per la stabilità è il potenziale a corta portata. Poiché abbiamo visto che R_min tende a zero con N → ∞, nei casi di instabilità questo risultato vale anche per il potenziale di Yukawa exp^-μ∣x∣/∣x∣, poiché esso ha lo stesso comportamento per ∣x∣ → 0. La singolarità del potenziale 1/∣x∣ all'origine è determinante. In effetti se si cambia U in

si può dimostrare (v. Thirring, 1977-1980) che

e perciò se la carica di tutte le particelle ha lo stesso valore assoluto, cioè se e²_i = e², il potenziale è maggiore o uguale a - Ne²μ e il sistema è stabile anche nel caso dei bosoni. Sorprendentemente questo dimostra che mentre per il potenziale di Yukawa la stabilità richiede una dimostrazione separata e non consegue dalla stabilità per il potenziale coulombiano, quest'ultima è un corollario della stabilità di Yukawa. Questo perché si può scrivere H = (K + U_y) + (U - U_y) e perciò, se la prima parentesi è maggiore o uguale a - cN, si ha stabilità, poiché la seconda parentesi è maggiore o uguale a - Ne²μ. Pertanto, il comportamento del potenziale a corta portata sembra determinare la stabilità. Se tuttavia si rimuove la singolarità in modo che il potenziale sia non monotono, cioè

il sistema diventa instabile anche per i fermioni. Questo perché se u (r₀) >u (0), la configurazione con la minima energia potenziale è quella in cui tutte le N/2 cariche positive sono addensate in una regione con un diametro r_m ≪ r₀, mentre le N/2 cariche negative si addensano in una regione della stessa dimensione a una distanza r₀ dalla prima. In questo caso la repulsione tra cariche positive e tra cariche negative dà un'energia potenziale

mentre l'attrazione tra le due regioni dà

Il risultato complessivo è il seguente:

U ∝ - N² (u (r₀) - u (0))/4;

questa energia negativa proporzionale a - N² non può essere compensata dall'energia cinetica positiva che, anche nel caso dei fermioni, è soltanto proporzionale a N^5/3 e perciò inferiore per N sufficientemente grande. La stessa conclusione vale anche se u è di corta portata e non singolare come u (x) = (1 + 2x) exp^-∣x∣. Ne consegue che non è né la lunga portata né la singolarità del potenziale 1/∣x∣ a produrre l'instabilità; il problema è assai più sottile. La mancanza, nei precedenti ragionamenti qualitativi, di questi più dettagliati aspetti del problema non permette di ottenerne la soluzione; a tal fine è pertanto necessaria una dimostrazione rigorosa che verrà presentata sommariamente nel prossimo capitolo, affinché il lettore possa farsi un'idea del tipo di matematica che deve essere utilizzata.

3. La dimostrazione

Il Faust di Goethe si chiede che cosa tenga il mondo unito nel suo profondo (was die Welt im Innersten zusammenhält?). Come abbiamo visto, questa è la domanda sbagliata, poiché le forze tra elettroni e nuclei sono tali che ogni parte può sempre trovare una nicchia attrattiva. La domanda da porsi è invece che cosa impedisca al mondo di collassare, visto che si è in presenza di tante forze attrattive. Oggi possiamo rispondere a questa domanda: a salvarci dal collasso non è una forza misteriosa, ma una proprietà particolare degli elettroni, la loro statistica di Fermi.

L'equazione di Schrödinger (4) è una legge valida in moltissimi casi. Essa non è però esatta, poiché trascura le correzioni dovute alla teoria della relatività e il campo elettromagnetico; a parte queste correzioni non sono state trovate altre eccezioni a quanto essa predice. Per questo è ragionevole supporre che essa determini non solo il comportamento degli atomi e delle molecole, ma anche quello di oggetti macroscopici e addirittura quello delle stelle. Non c'è da stupirsi che la letteratura fisica sia piena di tentativi di dedurre da questa equazione ogni sorta di curiosa proprietà presentata da sostanze particolari. Per N grande questo compito è solitamente troppo difficile e si ricorre ad approssimazioni incontrollabili o a versioni semplificate della (4), contenenti parametri liberi da aggiustare per accordarsi con i dati sperimentali. Il valore di questi risultati è discutibile e la vera pietra miliare per la scienza fu posta nel 1967, quando Dyson e Lenard (v., 1967) dedussero dalla (4) la seguente disuguaglianza,

H_N > - cN,

valida per ogni valore di N, dove c rappresenta una certa energia. Questo risultato dimostrò la stabilità di tutte le sostanze indipendentemente dal loro stato o dalla loro composizione chimica e tale dimostrazione rappresentò un eroico tour de force, concentrato in 40 pagine di difficile matematica. Purtroppo, se un'analisi diventa troppo complicata difetta anche di precisione: se in ogni pagina si ricorre a una disuguaglianza valida entro un fattore 2, dopo 40 pagine si è perso un fattore 2⁴⁰. In effetti, la costante c che ottennero Dyson e Lenard era di circa 2⁴⁰ volte il valore E₀ della (5), che dovrebbe essere il valore corretto. Riporteremo invece la dimostrazione di Lieb e Thirring (v., 1975), per la quale ci vollero solo tre pagine e che dà il valore di c a meno di un fattore ~ 8, che traduce gli argomenti intuitivi esposti nel capitolo precedente in disuguaglianze matematiche rigorose.

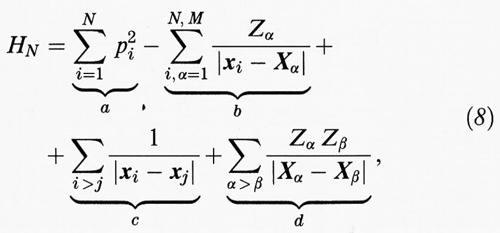
Come primo passo dobbiamo specializzare H_N della (1) per il caso in cui si tratti di corpi macroscopici. Come vedremo, la gravitazione diventa dominante solo per corpi della dimensione di Giove, dopodiché compromette la stabilità; porremo pertanto G = 0. La materia è costituita da elettroni e nuclei. Questi ultimi sono talmente più pesanti che la loro energia cinetica p²/2m non è rilevante, e pertanto la trascureremo. Essa è in ogni caso positiva e, se possiamo dimostrare H_N ≥ - cN supponendo che i nuclei abbiano massa infinita, cioè energia cinetica uguale a zero, l'ineguaglianza varrà a fortiori anche quando in H_N includiamo l'energia cinetica dei nuclei. Inoltre, tutti i nuclei hanno degli isotopi che sono bosoni e perciò la stabilità deve valere anche per essi; peraltro, dal momento che abbiamo tralasciato l'energia cinetica, la struttura isotopica dei nuclei non ha più importanza. Consideriamo allora un sistema di N elettroni con coordinate e quantità di moto (x_i, p_i), i = 1, ..., N, e M ≤ N nuclei con coordinate e cariche X_α e Z_α, α = 1, ..., M (le quantità di moto nucleari non appariranno). Usando ancora unità atomiche, l'hamiltoniana diventa

dove il termine a è l'energia cinetica degli elettroni che va sostituita con l'operatore differenziale - Σ_i ∂²/∂x²_i nell'equazione di Schrödinger; b rappresenta l'attrazione degli elettroni, mentre c e d indicano, rispettivamente, la repulsione elettrica degli elettroni e dei nuclei. La dimostrazione della stabilità si riduce dunque a dimostrare che per qualsiasi funzione ψ (x_i, ..., x^N) con ∫ dx^N∣ψ∣² = 1, e antisimmetrica nelle x_i, esiste una costante c tale che

dove c può dipendere dalle cariche nucleari Z_α ma non dalle loro posizioni X_α e da N. In realtà abbiamo semplificato molto il problema ignorando lo spin degli elettroni, ma questo risulta essere una complicazione inessenziale e pertanto la ignoreremo in questa sede. La chiave per dimostrare la stabilità è la teoria di Thomas-Fermi (TF), secondo la quale la nube di elettroni dovrebbe comportarsi come un liquido la cui pressione P non dipende linearmente, come nel caso di un gas perfetto a temperatura fissata, dalla densità ρ degli elettroni, ma da ρ^5/3. Questo corrisponde alla nostra considerazione euristica in cui abbiamo trovato che nel caso di fermioni

e perciò

Allo stesso modo si assegna al fluido di elettroni un'energia cinetica interna proporzionale a ρ^5/3 e perciò si sostituisce l'energia cinetica del termine a con:

Abbiamo inserito il valore numerico corretto che tiene conto anche dello spin. I termini rimanenti, come risulta evidente nelle ipotesi del modello TF, sono:

dove si vede, paragonando la (8) e la (9), che a causa dell'antisimmetria della ψ dobbiamo identificare la densità degli elettroni con:

La repulsione degli elettroni (termine c) diviene:

che dovrebbe derivare dalla (8) e dalla (9) se in ψ non ci fosse alcuna correlazione tra gli elettroni. Il termine d non contiene le coordinate degli elettroni e rimane perciò inalterato, d = d_TF. Pertanto, nella teoria TF il problema si riduce a cercare il minimo E_TF (Z₁, ..., Z_M) di a_TF + b_TF + c_TF + d_TF al variare di ρ. In questo modello la stabilità diventa banale in conseguenza del seguente teorema enunciato da E. Teller e dimostrato da Lieb e Simon (v., 1977):

E_TF (Z₁, ..., Z_M) ≥ E_TF (Z₁, ..., 0) +

+ E_TF (0, Z₂, 0, ..., 0) + ... + E_TF (0, ..., Z_M) (14)

dal quale si possono trarre alcune osservazioni: 1) il teorema dimostra che nella teoria TF non vi è alcun legame chimico: l'energia del sistema composto è superiore alla somma delle energie degli atomi individuali; 2) mentre il primo membro della (14) dipende dalle X_α, il secondo membro è indipendente da esse e perciò si ottiene un limite inferiore di E indipendente dalle coordinate nucleari; 3) la (14) dimostra la stabilità poiché nella teoria TF il valore minimo di E_TF si raggiunge nel caso di un sistema neutro, in cui cioè

, e quindi anche per N ≥ M, essendo E monotona in Z, si ha:

E_TF (Z₁, ..., Z_M) ≥ - N E_TF (Z_max, 0, ..., 0), se Z_α ≤ Z_max ∀ α.

Senza entrare nei dettagli della dimostrazione della (14), facciamo notare che questa non significa che il fluido di elettroni non ‛preferisca' che le cariche nucleari siano fra loro vicine; gli elettroni in effetti producono una certa attrazione fra i nuclei che tuttavia non è sufficientemente forte da superare la repulsione nucleare (d ). Senza (d ) la disuguaglianza (14) va nell'altra direzione, il che dimostra che l'effetto è davvero sottile.

Pertanto, data la stabilità nella teoria TF, dobbiamo chiederci se questo si verifichi anche per l'equazione di Schrödinger che il modello TF dovrebbe imitare. Abbiamo visto che la sostituzione di b e d con b_TF e d_TF è esatta, cosicché rimangono i due seguenti problemi.

1) Sostituzione a → a_TF: l'energia cinetica per una funzione d'onda ψ (x₁, ..., xN) può essere scritta nella seguente maniera:

che deve essere paragonata al valore a_TF che si ottiene dalla (10). Ciò che si deve dimostrare è che ∫ ρ^5/3 (x) dx non può crescere senza che cresca anche il quadrato della derivata di ψ. La plausibilità di questa affermazione è intuitiva e infatti vi è un'ineguaglianza dovuta al matematico russo L. S. Sobolev che, nel caso di una particella, stabilisce:

Poiché richiediamo che ∫ dx ρ (x) = 1, il secondo membro, per effetto della disuguaglianza di Hölder, è maggiore di ∫ ρ^5/3 (x)x, che è quanto volevamo dimostrare. Nel caso di N particelle non è possibile ottenere tanto facilmente questo risultato, poiché, come abbiamo visto, esso non è valido nel caso dei bosoni. Perciò è essenziale tener conto della natura fermionica, cioè dell'antisimmetria di ψ (x₁, ..., x_N) in tutti i suoi argomenti. Nella derivazione elementare della (16), non vi è spazio per incorporare l'antisimmetria, ma anche in questo caso, con un po' di intuizione fisica, riusciremo a trovare la soluzione. Per una particella in un potenziale esterno u esiste un limite superiore per i valori permessi di energia negativa E_i, e precisamente (v. Lieb e Thirring, 1975):

dove u_- è la parte negativa di u. Questo comportamento è quello che ci dobbiamo aspettare perché, integrando le energie negative nello spazio delle fasi classico, otteniamo:

che, a parte il fattore 4π, coincide con il risultato precedente. Se consideriamo ora N fermioni nel potenziale esterno u, l'autovalore minimo dell'hamiltoniana

si ottiene riempiendo successivamente i valori negativi di p² + u; essa risulta perciò maggiore di

Ora, data una ψ (x₁, ..., x_n) costruiamo ρ (x) per mezzo della (12) e consideriamo il potenziale u (x) = - Kρ (x )^2/3, dove K è un numero da determinarsi in seguito. Sappiamo già che

è un limite superiore dell'autovalore più basso ed è perciò maggiore di

Troviamo così una disuguaglianza del tipo a>c ∫ ρ^5/3. Ottimizzando rispetto a K e prendendo in considerazione lo spin, si ottiene più precisamente:

a ≥ (4π)^-2/3 a_TF. (20)

2) Sostituzione c → c_TF: come già detto, sostituire c con c_TF significa trascurare le correlazioni tra gli elettroni. Per effetto della statistica di Fermi e della repulsione coulombiana, gli elettroni tendono a mantenersi a distanza e occorre perciò chiedersi quanto questo effetto farà diminuire c. Una risposta si ottiene dalla teoria TF, poiché se si applica la (14) al caso di Z_i = 1, i = 1, ..., M = N, otteniamo:

Il parametro λ è proporzionale alla massa dell'elettrone che abbiamo reintrodotto per dare maggiore flessibilità alla disuguaglianza che vale per tutti i λ > 0. Inoltre, abbiamo utilizzato il valore numerico di E (1, 0, ..., 0). Poiché E era il valore minimo del primo membro della (21), la disuguaglianza vale per ogni ρ e si ottiene così per ogni ρ e λ > 0:

Di conseguenza, la repulsione coulombiana delle cariche positive nel punto X_α è sempre maggiore dell'energia potenziale di queste cariche in un potenziale prodotto da una densità di carica ρ alla quale vanno sottratti alcuni termini correttivi. Il primo è la self-energia di ρ, e gli altri sono l'‛energia cinetica' di ρ (con una massa ∝ λ) e un'energia ∝ N. Questa disuguaglianza non dipende dal fatto che la carica nucleare è positiva, e può quindi essere utilizzata per la repulsione degli elettroni nella (8). Perciò H_N è limitato inferiormente da un'hamiltoniana di N particelle in un campo esterno creato dalla densità di carica ρ che possiamo scegliere a piacere. Se calcoliamo ∫ ψ^* Hψ, possiamo scegliere di usare per ρ il valore corrispondente a ψ, nel qual caso i primi due termini a secondo membro della (22) diventano pari a 1/2 ∫ (dx dy ρ (x) ρ (y))/∣x - y∣, che coincide con il valore di c della teoria TF. La correzione ∝ ∫ ρ^5/3 può essere combinata con il termine a e produce solo una variazione del fattore che moltiplica a; l'ultimo termine nella (22) si comporta come N. Così, ∫ ψ^* Hψ è limitato inferiormente da un funzionale del tipo di quello della teoria TF e, se si usa nuovamente la (14), si ottiene un limite inferiore che si comporta come N. La conclusione esatta, usando E (Z, 0, ..., 0) = Z^7/3 E (1, 0, ..., 0) e ottimizzando rispetto a λ, è la seguente:

Benché il numero nella (23) non sia esageratamente grande, non è neppure ottimale per le seguenti ragioni.

1) La (17) è derivata con un metodo non molto raffinato e la costante, che non è certo molto precisa, in effetti è stata leggermente migliorata. Si pensa tuttavia che questa disuguaglianza dovrebbe risultare valida anche con la costante della (18). L'esattezza di questa congettura non è ancora stata dimostrata, ma neppure si è dimostrato il contrario. Se fosse esatta si potrebbe ottenere, anziché la (20), il risultato ottimale a ≥ a_TF. Inoltre, benché il risultato della (14) sia un valore ottimale (il segno uguale si ottiene se ∣X_α - X_β∣ → ∞ per α ≠ β) non è ottimale come limite alla repulsione coulombiana. In effetti, Lieb e Oxford (v., 1981) hanno ottenuto la disuguaglianza c ≥ c_TF - 8,5 ∫ ρ^4/3. Una correzione di questo tipo era già stata proposta da Paul Dirac per tener conto della statistica di Fermi per gli elettroni. Per questo motivo, se la congettura si rivelasse esatta, la teoria TF, con una correzione ∫ ρ^4/3, darebbe un limite inferiore per l'energia dello stato fondamentale di tutte le sostanze. Numericamente l'energia TF è inferiore di circa il 20% al valore delle energie osservate e questo è presumibilmente il miglior risultato ottenibile per un limite di tale generalità.

2) Usando la (14) per trovare un limite a H_N tramite una hamiltoniana di particelle in un campo esterno, occorre soltanto la (17) per ottenere il limite (23) senza dover passare per l'energia cinetica. Ma in questa maniera si otterrebbero gli stessi numeri e non si perderebbe niente passando attraverso l'energia cinetica (v. Thirring, 1975; v. tab. II).

4. Conseguenze

a) Stabilità relativistica

La hamiltoniana (1) descrive correttamente particelle con velocità molto minore della velocità c della luce. Avvicinandosi a c (‛velocità relativistiche'), compaiono dei fenomeni nuovi che sono contenuti nella teoria della relatività di Einstein. Esiste una teoria, detta elettrodinamica quantistica, che combina la teoria della relatività speciale con la meccanica quantistica e include i fenomeni elettromagnetici. Benché tutte le sue predizioni siano state verificate sperimentalmente con un'accuratezza senza precedenti, questa teoria non ha ancora raggiunto un grado di sviluppo matematico tale da consentire di dedurne il teorema della stabilità. Un effetto cinematico della teoria della relatività, cioè la particolare dipendenza dell'energia cinetica dalla quantità di moto, può tuttavia essere incorporato facilmente nella (1). L'energia cinetica è data da

,

il cui primo termine nello sviluppo in serie di potenze di p²/m²c² è il termine non relativistico p^2/2m. Per semplificare la notazione, non useremo come unità di misura del tempo il secondo, ma il tempo impiegato dalla luce per percorrere un'unità di lunghezza, per cui mc² diventa semplicemente m. Ne consegue che per p ≫ m, l'energia aumenta solo in maniera lineare con p, ossia, in meccanica quantistica, con 1/Δx. Per questo il gas di elettroni con velocità vicina a c diventa più ‛soffice' di quanto non sia in una situazione non relativistica; la pressione, cioè, si comporta come ~ ρ^4/3 invece che come ρ^5/3. Di conseguenza, l'instabilità diventa più catastrofica poiché l'energia cinetica si comporta come ~ 1/Δx, cioè come l'energia potenziale. Se quest'ultima ha un coefficiente maggiore, l'energia minima va a - ∞ e si raggiunge per Δx → 0. Perciò, invece di un limite all'energia totale non lineare in N, otteniamo un collasso completo per un N determinato senza alcun limite inferiore all'energia. Infatti, se si ripetono le considerazioni euristiche del cap. 2, sostituendo p²/2m con

si ottengono i quattro casi della tab. II.

Perciò l'unico caso che non dia luogo a una catastrofe è quello dei fermioni con interazioni elettrostatiche e α = Ze² 〈 1. In tutti gli altri casi il sistema collassa completamente per un N sufficientemente grande. Tutti questi risultati disastrosi possono essere avvalorati da un'analisi matematica rigorosa (v. Lieb, 1991) che, tuttavia, è alquanto più complessa della dimostrazione della stabilità delineata nel cap. 3 e non può essere riprodotta in questa sede.

Paragonando le tabb. I e II si può comunque facilmente derivare un'interessante conseguenza: il confronto mette infatti in evidenza come un comportamento non relativistico dell'energia E ∝ - cN^γ, γ > 1, implica che nel caso relativistico E tenda a - ∞ per un dato N. Le disuguaglianze

dimostrano che la stabilità (nel senso di E ∝ N) non dipende dalla massa poiché

cosicché l'energia cinetica, con o senza massa, differisce solo per il termine Nm. Se l'energia cinetica non relativistica p²/2m si comporta come - N^γ, γ > 1, ne consegue che nel caso relativistico per certi valori di N l'energia diventa negativa poiché

In questo caso però l'energia è negativa anche per m = 0 e pertanto si può renderla arbitrariamente negativa facendo tendere Δx → 0. Invero, per m = 0 l'hamiltoniana non contiene alcuna lunghezza e, per effetto della dilatazione x → l^-1x, p → lp si ha H → lH per qualsiasi l > 0. Per questo motivo, se vi è una ψ tale che ∫ ψ^* Hψ = E 〈 0, cambiando ψ (x) in ψ (l^-1x) si ottiene, in luogo di E, lE e quindi, nel limite l → ∞, si ottengono energie negative arbitrariamente grandi.

A questo punto ci si potrebbe domandare dove in natura si abbiano conseguenze tanto catastrofiche dell'instabilità. Nel caso elettrico le cose possono volgere al peggio quando α = Ze² → 1. In unità ℏ = c = 1, abbiamo e² = 1/137 perciò occorre una carica elettrica nucleare maggiore di 137. Finora non è stato trovato nessun nucleo stabile con una carica del genere, ma per un breve tempo si possono raggiungere cariche nucleari anche maggiori. Per esempio, facendo scontrare due nuclei di piombo si ottiene per un breve intervallo di tempo un nucleo con Z = 164. In questo caso, però, si produce un altro effetto previsto dalla teoria della relatività, e cioè la creazione di coppie di elettroni-positroni nel vuoto. I positroni vengono espulsi e gli elettroni schermano la carica nucleare rendendola subcritica.

Nel caso di bosoni carichi, il sistema diventa catastrofico già con Z = 1 se N > α^-3, cioè circa dieci milioni. Tuttavia, non esistono bosoni elementari stabili carichi e perciò questo tipo di fuochi d'artificio non si presenta in natura. Si noti che la nostra discussione non si applica ai nuclei di deuterio o di elio che non possono essere considerati elementari perché composti da protoni e neutroni.

In natura l'instabilità si manifesta solo se entra in scena la gravità; poiché essa è sempre presente, viene da domandarsi come mai si realizzi la stabilità sulla Terra. È facile valutare in che condizioni gli effetti della gravità diventino preponderanti rispetto a quelli dell'elettricità. A tal fine osserviamo che la nostra hamiltoniana originale (1) può essere scritta nella forma:

cosicché, secondo la tab. I, otteniamo un limite inferiore (trascurando i fattori numerici) che si comporta proporzionalmente a - (e⁴N + G²N^7/3). L'instabilità dovuta alla dipendenza da N^7/3 si verifica quando il secondo termine supera il primo; poiché e² ~ 10^-2 e G ~ 10^-38 (ponendo la massa del protone, ℏ e c uguali all'unità) i due termini sono dello stesso ordine quando 10^-2 = 10^-38 N^2/3, cioè quando N ~ 10⁵⁴, che corrisponde più o meno alla massa di Giove. Nel centro di Giove gli atomi si schiacciano e la materia si trasforma in un plasma. All'aumentare di N, la materia si comprime ulteriormente e secondo la tab. II gli elettroni raggiungono la velocità della luce per N ~ G^-3/2 ~ 10⁵⁷, che corrisponde più o meno alla massa del Sole. La materia diventa poi più soffice (quando la pressione si comporta come ρ^4/3) e si apre la strada al collasso completo. Tuttavia, perché ciò si verifichi occorre un meccanismo che liberi tutta l'energia potenziale della gravitazione. La radiazione elettromagnetica è troppo lenta per questo, poiché a causa della diffusione occorrono milioni di anni perché un fotone arrivi alla superficie dal centro del Sole. Tuttavia, quando l'energia degli elettroni è tale che il processo e + p → n + ν_e diventa possibile, i neutrini forniscono un meccanismo efficiente per eliminare l'energia gravitazionale e la situazione diventa drammatica. Infatti, i neutrini possono attraversare il Sole praticamente senza diffondere, cosicché la stella collassa nel giro di secondi come un pallone con tanti buchi dai quali può fuoriuscire il gas. Quando si raggiungono densità nucleari, il che accade quando il raggio della stella si è ridotto a circa 30 km, entrano in azione forze nucleari. A quel punto la materia torna a indurirsi e quel che fuoriesce comincia a rimbalzare creando un'onda d'urto che causa l'espulsione di parte del materiale caldo e l'implosione si trasforma in esplosione. A questo fenomeno, osservato alcune volte da astronomi e amatori, che si manifesta nell'improvviso aumento della luminosità di una stella che la fa splendere quanto una galassia intera, viene dato il nome di ‛supernova'.

A questo punto è opportuno introdurre due osservazioni: 1) il fatto che le stelle siano stabili fino a N = 10⁵⁷ è dovuto alla pressione degli elettroni che sono fermioni; la tab. II mostra infatti che se fossero bosoni l'instabilità gravitazionale interverrebbe per N ~ G^-1 = 10³⁸, che corrisponde più o meno al numero di protoni contenuti in una montagna. La materia bosonica sarebbe talmente soffice che oggetti più grandi sarebbero schiacciati dal loro stesso peso. 2) Qualora la stella di neutroni formata nell'esplosione della supernova abbia una massa corrispondente a diverse masse solari, essa collasserà ulteriormente per sparire in un buco nero di qualche chilometro di diametro. Per lungo tempo si è pensato che un buco nero rappresentasse una sorta di tomba che non rivela cosa sia seppellito al suo interno. In base a questa teoria, una supernova dovrebbe essere l'ultima e spettacolare manifestazione di instabilità termodinamica in un sistema gravitazionale che si conclude in un buco nero. J. Bekenstein (v., 1973) e S. Hawking (v., 1975) hanno però avanzato l'ipotesi che l'entropia S di un buco nero sia proporzionale alla sua superficie. Poiché il raggio è proporzionale alla sua energia E, allora S ∝ E², e questo implica che T = (∂S/∂E)^-1 ∝ 1/E e perciò il calore specifico (∂E/∂T) ∝ - E² diventa negativo. Perciò un buco nero irradierà e, perdendo energia, la sua temperatura aumenterà, aumentando di conseguenza l'irradiazione fino a un ultimo stadio nel quale si dissolverà nel nulla. Questo vuol dire che l'instabilità termodinamica dei sistemi gravitazionali persiste anche dopo la ‛tomba'.

b) L'esistenza di dinamiche locali

La fisica si basa sul presupposto che sia possibile isolare un sistema e considerarlo indipendente dal resto dell'universo. Per questo le equazioni relative alla particella 1 che si ottengono dalla hamiltoniana H_N della (1) dovrebbero tendere a un limite per N → ∞, se tutte le altre particelle sono sufficientemente distanti. Ciò è legato alla stabilità H_N > - cN, senza la quale l'energia di ciascuna particella potrebbe diventare arbitrariamente negativa e pertanto, a un'energia totale fissata, anche l'energia e la velocità di ciascuna particella aumenterebbero indefinitamente con N. Questo vuol dire che per N → ∞ il moto diviene sempre più veloce e l'evoluzione temporale non tende a un limite. Ora, è facile verificare questo andamento poiché i calcolatori attuali possono risolvere e visualizzare le soluzioni delle equazioni hamiltoniane (3) per, ad esempio, N ~ 10³ (v. Compagner e altri, 1989; v. Posch e altri, 1990). Nel caso di interazioni stabili, le particelle si muovono come un nugolo di zanzare e l'impressione visiva non cambia molto anche se si raddoppia N. Nel caso di interazioni instabili, invece, si forma un addensamento caldo che contiene una buona parte (N_c) di tutte le particelle. Raddoppiando N, raddoppia anche l'addensamento e poiché l'energia cinetica per particella è proporzionale a N_c, le particelle nell'addensamento si spostano più velocemente anche se inizialmente tutte le particelle avevano più o meno la stessa energia. Così, in questo caso l'evoluzione temporale tende a un limite solo a condizione che, se N tende all'infinito, si cambi anche la scala temporale in maniera da risolvere un moto ancor più veloce. Resta ancora aperto il problema relativo all'esistenza di una dinamica locale in una situazione stabile di fermioni con interazioni coulombiane. L'unica cosa che è stata dimostrata riguarda le interazioni che vanno a zero quando la quantità di moto relativa di due particelle va all'infinito. Nel caso dei fermioni queste interazioni sono stabili ed esiste il limite N → ∞ per l'evoluzione temporale senza cambiare la scala dei tempi (v. Narnhofer e Thirring, 1990).

c) Stabilità termodinamica

Nel caso delle interazioni che ci interessano, vale la subadditività dell'energia e di conseguenza, in base al teorema illustrato nel cap. 1, (O) e (C) sono equivalenti. In particolare, se domina la gravità il limite (7) non esiste ma va sostituito da

allora anche (O), e di conseguenza anche (C), non valgono, il che significa che il sistema deve avere un calore specifico negativo. Questa è in effetti la caratteristica dominante nell'evoluzione di una stella: alla sua nascita il gas interstellare forma addensamenti caldi come descritto nel precedente § b; quando queste condensazioni divengono così calde da irradiare, perdono energia e di conseguenza diventano ancora più calde a causa del calore specifico negativo. Questo fenomeno continua fino a che al centro dell'addensamento si raggiungono i 20 milioni di gradi e il combustibile nucleare inizia a bruciare; la perdita di energia allora si ferma, poiché la quantità di energia sviluppata nel centro è uguale a quella irradiata dalla superficie. Poiché l'energia rimane costante, si stabilizza anche la temperatura. Per quanto strano possa apparire, ciò significa che il combustibile nucleare non è la causa del riscaldamento ma, al contrario, diventa la causa del raffreddamento di una stella, perché in sua assenza la temperatura continuerebbe a crescere. Questo avviene quando il combustibile nucleare è consumato e, se la stella è abbastanza pesante, si verificherà la manifestazione spettacolare descritta nel cap. 2, § a.

Per corpi più piccoli, come la Terra, nei quali la materia è dominata dalle forze elettrostatiche, la condizione (O) è soddisfatta e il teorema descritto nel cap. 1 asserisce che tutte le sostanze, indipendentemente dalla loro composizione chimica, devono avere un calore specifico positivo. Benché le sostanze con calore specifico negativo siano pericolose, dobbiamo la nostra esistenza all'interscambio fra stabilità su scala terrestre e instabilità su scala cosmica; infatti, ciò che rende possibile la vita è fondamentalmente la luce solare, che è ricca di energia ma a basso contenuto di entropia. L'entropia della radiazione elettromagnetica è data essenzialmente dal numero di fotoni, la cui energia è proporzionale alla temperatura del luogo da cui sono stati emessi. Perciò i fotoni della luce solare hanno un'energia di circa 6.000 K, quella della superficie del Sole, e da ciascuno di essi si possono ottenere 20 fotoni con un'energia di 300 K, equivalente alla temperatura terrestre, senza violare il principio della conservazione dell'energia. In tal modo, l'entropia della luce solare aumenta di un fattore 20 ed è possibile perciò creare delle strutture ordinate con entropia inferiore, quali gli esseri umani, senza diminuire l'entropia totale e cioè senza violare la seconda legge della termodinamica. La nostra vita dipende dunque dalla differenza di temperatura tra il Sole e la Terra, e se la morte termica avesse stabilito l'equilibrio in tutto l'universo, la vita non esisterebbe. È lecito domandarsi come mai l'universo non sia in equilibrio perfetto, visto che la radiazione di fondo di 3 K testimonia che, nelle sue fasi iniziali, l'universo aveva una distribuzione di temperatura molto omogenea. La spiegazione sta nel fatto che con l'espandersi dell'universo furono raggiunte regioni dello spazio delle fasi in cui si avevano calori specifici negativi poiché si formavano addensamenti caldi, cioè le stelle. Sebbene questa differenza di temperatura sia solo un fenomeno transitorio e non uno stato stazionario, possiamo nel frattempo goderci sia il Sole sia la stabilità locale.

Bibliografia

Bekenstein, J. D., Black holes and entropy, in ‟Physical review. D", 1973, VII, pp. 2333-2346.

Compagner, A., Bruin, C., Roelso, A., Collapsing systems, in ‟Physical review. A", 1989, XXXIX, pp. 5989-6002.

Dyson, F. J., Lenard, A., Stability of matter I, in ‟Journal of mathematical physics", 1967, VIII, pp. 423-434.

Fisher, M., Ruelle, D., The stability of many-particle systems, in ‟Journal of mathematical physics", 1966, VII, pp. 260-270.

Hawking, S., Particle creation by black holes, in ‟Communications in mathematical physics", 1975, XLIII, pp. 199-200.

Lebowitz, J. L., Lieb, E. H., The existence of thermodynamics for real matter with Coulomb forces, in ‟Physical review letters", 1969, XXII, pp. 631-634.

Lieb, E. H., Stability of matter, in Atoms to stars (a cura di W. Thirring), Berlin-New York 1991.

Lieb, E. H., Oxford, S. J., Improved lower bound on the indirect Coulomb energy, in ‟International journal of quantum chemistry", 1981, XIX, pp. 427-439.

Lieb, E. H., Simon, B., The Thomas-Fermi theory of atoms, molecules and solids, in ‟Advances in mathematics", 1977, XXIII, pp. 22-116.

Lieb, E. H., Thirring, W., Bound for the kinetic energy of fermions which proves the stability of matter, in ‟Physical review letters", 1975, XXXV, pp. 687-689.

Lieb, E. H., Thirring, W., Universal nature of van der Waals forces for Coulomb systems, in ‟Physical review. A", 1986, XXXIV, pp. 40-46.

Narnhofer, H., Thirring, W., Quantum field theories with Galilei invariant interactions, in ‟Physical review letters", 1990, LXIV, pp. 1863-1866.

Posch, H. A., Narnhofer, H., Thirring, W., Dynamics of unstable systems, in ‟Physical review. A", 1990, XLII, pp. 1880-1890.

Thirring, W., Berechenbare Eigenschaften der Materie, in ‟Physikalische Blätter", 1975, XXXI, pp. 582 ss.

Thirring, W., Lehrbuch der mathematischen Physik, 4 voll., Wien-New York 1977-1980.