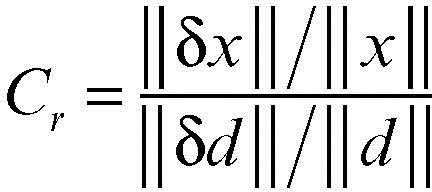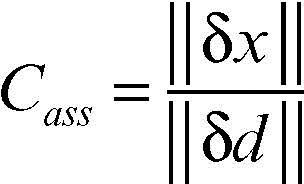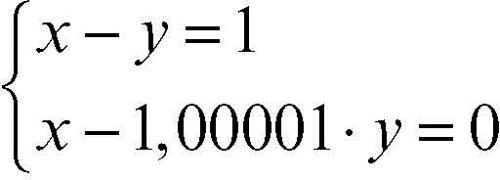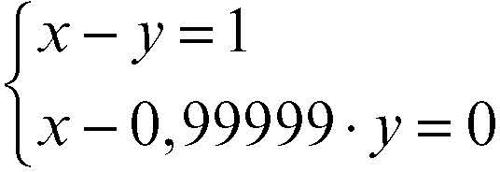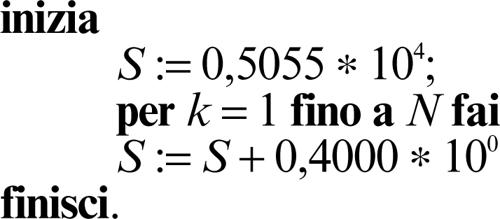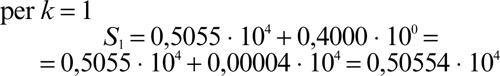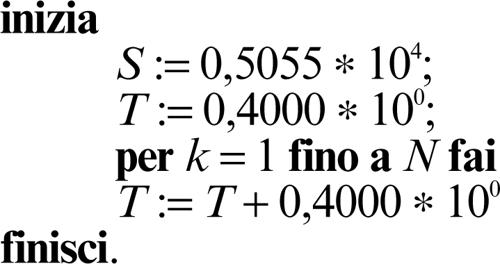algoritmo, stabilità di un
algoritmo, stabilita di un
algoritmo, stabilità di un capacità di un algoritmo di fornire in output risultati attendibili quando l’insieme dei dati in input cambia, sia come valori sia come quantità di dati iniziali. Si supponga di dover trovare la soluzione x del problema generale P(x) = d, dove d rappresenta genericamente un dato numerico del problema e P la relazione funzionale, caratteristica del problema in esame, che lega x e d. Si tratta di un → problema ben posto se per un certo dato d la soluzione di P(x) = d esiste, è unica e dipende con continuità da d. Quest’ultima proprietà implica che piccole modifiche del valore di d diano origine a piccole variazioni della soluzione x, sia percentualmente sia in valore assoluto.
Tenendo conto delle caratteristiche dell’aritmetica finita propria di un automa esecutore (→ aritmetica finita (di macchina)) e degli errori di approssimazione, un algoritmo si dice stabile se la propagazione degli errori dovuta ai calcoli è limitata e controllabile a priori. Un algoritmo è più stabile di un altro se l’influenza degli errori nel primo è minore che nel secondo. In generale si può affermare che la stabilità di un algoritmo dipende da due fattori concomitanti: il primo è l’alterazione della soluzione in funzione dell’alterazione dei dati iniziali; il secondo è la modalità di propagazione degli errori.
Il primo fattore è direttamente connesso con la proprietà di dipendenza continua della soluzione dai dati, e non dipende dall’uso dell’aritmetica finita di macchina ma dal problema stesso e dalla sua implementazione algoritmica. Formalmente, se si opera una variazione ∗d del dato ci si può chiedere quanto valga la variazione ∗x della soluzione che risolve il problema P(x + ∗x) = d + ∗d.
Si può effettuare una stima quantitativa di questa dipendenza introducendo l’indice di condizionamento relativo del problema
Se x = 0, d = 0 si può calcolare l’indice di condizionamento assoluto del problema tramite la relazione
Se Cr è grande, il problema P è mal condizionato forse perché mal posto; ma se P è ben posto e Cr è grande, occorre riformulare il problema in altro modo.
Per esempio, si consideri il problema di trovare la soluzione del seguente sistema
La soluzione è x = 100.001; y = 100.000. Se si opera una piccola variazione nel coefficiente della y scrivendo al posto di −1,00001 il valore −0,99999
si trova la soluzione x = −99.999; y = −100.000.
La variazione sui dati è ∗d = −0,99999 + 1,00001 = 2 · 10−5, ma ha causato un’alterazione molto grande nella coppia di numeri soluzione del sistema
Infatti l’indice di condizionamento relativo in questo caso è molto grande e vale Cr = 2 · 1010.
Oltre alla dipendenza della soluzione dai dati, gioca un ruolo importante nella stabilità la propagazione degli errori dovuti all’aritmetica finita della macchina. Si consideri, per esempio, un algoritmo per il calcolo della successione delle seguenti somme parziali, avendo a disposizione 4 cifre per la mantissa; successione che si può scrivere in forma ricorsiva:
Utilizzando questa formula si scrive l’algoritmo di somma
Tuttavia se si esegue, passo dopo passo, il calcolo effettivo, senza considerare le limitazioni sulla mantissa si ottiene
che viene approssimato a 0,5055 · 104;
e così via. Il risultato è costante, sempre uguale al primo termine della sommatoria. Questo esempio estremo mostra che l’algoritmo così definito è notevolmente instabile, in quanto l’aritmetica finita della macchina a disposizione non permette di effettuare la corretta sommatoria desiderata, fornendo sempre un risultato costante, pur aggiungendo un termine diverso da 0 a ogni iterazione. Si può modificare l’algoritmo nel modo seguente per ottenere il risultato corretto:
A ogni passo il calcolo viene effettuato efficacemente perché coerente con l’implementazione numerica a disposizione (4 cifre per la mantissa). Per N = 10 si ottiene per esempio T = 0,0004 · 104 e il risultato finale non risulta affetto dall’errore precedente:
Questa è una regola generale per la somma di numeri macchina; infatti, per minimizzare la propagazione degli errori, è necessario eseguire la somma dal più piccolo al più grande.