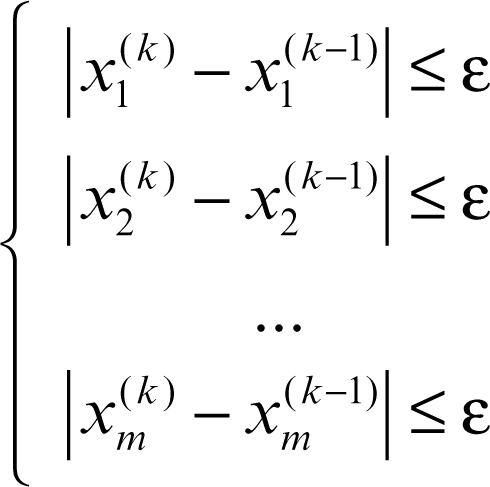soluzione, stabilita di una
soluzione, stabilita di una
soluzione, stabilità di una proprietà della soluzione approssimata di una equazione ƒ(x) = 0 nel caso in cui tale soluzione venga ottenuta con un → metodo numerico iterativo convergente. La soluzione così calcolata si definisce stabile se, fissato il passo n dell’iterazione in cui vale |x(n) − x(n−1)| < ε (cioè il valore assoluto della differenza tra i valori approssimati, ottenuti in due passi di calcolo successivi, è minore di una quantità ε positiva prefissata), la disuguaglianza rimane verificata per tutti i passi ulteriori: ∀k ≥ n, |x(k) − x(k−1)| < ε.
Si osservi che in apice tra parentesi è indicata l’iterazione a cui ci si riferisce. Questa definizione si generalizza anche al caso dei sistemi di equazioni lineari di m equazioni in m incognite. In questo caso la soluzione, ottenuta con metodi opportuni, come il metodo di → Jacobi o il metodo di → Gauss-Seidel, è una m-pla di valori che dalla n-esima iterazione in poi soddisfa le condizioni:
Questo sistema di condizioni generalizza la condizione precedente, riferita a una equazione, indicando che, per ciascuna delle variabili xi con i = 1, …, m, la differenza tra un’iterazione e la precedente è, da una certa iterazione in poi, minore di ε positivo prefissato.
La stabilità di una soluzione non coincide sempre con la convergenza della soluzione, perché quest’ultima dipende da alcune ulteriori condizioni necessarie che devono verificarsi contemporaneamente: a) la convergenza del metodo numerico usato (→ algoritmo, convergenza di un); b) la stabilità dell’algoritmo implementato nel metodo numerico; c) la scelta opportuna della condizione di arresto delle iterazioni.
Il valore ε che compare nelle condizioni precedenti è un numero reale positivo che indica il grado di precisione desiderato, ossia quante cifre decimali esatte si desidera ottenere: ε è perciò in genere molto piccolo, ma non lo può essere arbitrariamente, perché può accadere che, a causa degli errori di arrotondamento dovuti all’→ aritmetica finita di macchina, le condizioni sulla precisione di calcolo non si verifichino mai per alcun indice n. Si vedano anche → approssimazione (di una soluzione); → equazione, metodo numerico per la risoluzione di una; → algoritmo, stabilità di un.