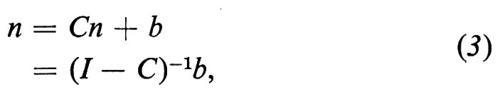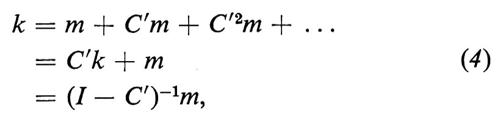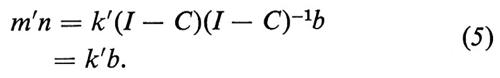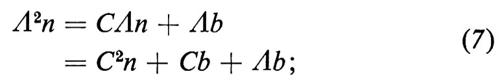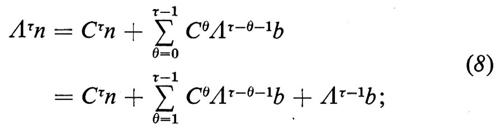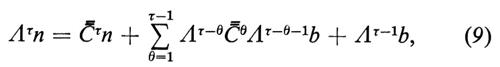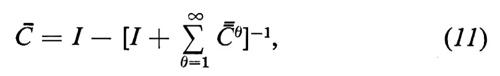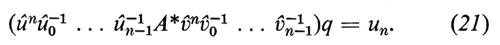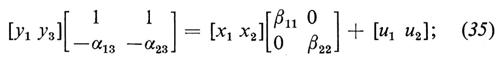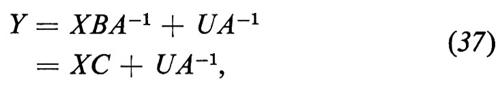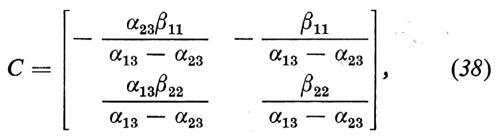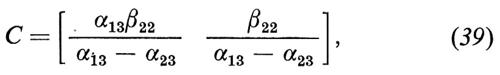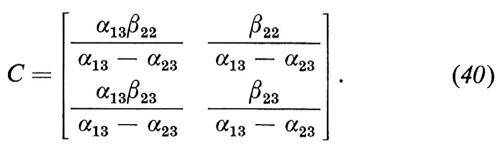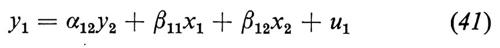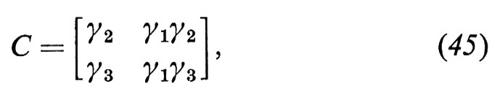Statistica

Statistica

di Richard Stone

sommario: 1. Introduzione. 2. Economia, società e ambiente. 3. Economia: il sistema dei conti nazionali. 4. Sistemi alternativi. 5. Benessere e sistema dei conti nazionali. 6. Demografia sociale: verso un sistema di statistiche sociali e demografiche. 7. L'ambiente: un futuro sistema di statistiche dell'ambiente? 8. Problemi di applicazione. 9. Classificazione, raggruppamento e aggregazione. 10. Coerenza, aggiustamento delle osservazioni e aggiornamento. 11. Identificazione, sistemi e stima. 12. Previsioni e proiezioni. 13. Politica, ottimizzazione e controllo. 14. Conclusioni. □ Bibliografia.

1. Introduzione

Il termine ‛statistica' viene usato in molteplici accezioni. In primo luogo esso può indicare un corpo di dati quantitativi, come nel caso delle statistiche dell'istruzione o delle statistiche sociali in genere. In secondo luogo, quando si parla, per es., di statistica matematica, può denotare un insieme di tecniche fondate principalmente, ma non esclusivamente, sulla teoria della probabilità, tecniche che sono utili nell'analisi di molte specie di dati numerici. In terzo luogo può indicare, in riferimento a stime campionarie, una misura che abbia una qualche ben definita e desiderabile proprietà, come quando parliamo, con R.A. Fisher (v., 1925), di statistiche efficienti o di statistiche sufficienti. Pertanto il termine statistica può essere impiegato sia per indicare i dati osservati oppure gli strumenti usati nella loro analisi, sia per distinguere misure che abbiano raggiunto un buon livello di precisione da altre che non lo hanno raggiunto.

La rilevazione di dati statistici interessa quasi tutti i rami della scienza: a parte quelle relative all'economia e alle altre scienze sociali, esistono statistiche che riguardano la fisica, la chimica, la meteorologia, la biologia, l'archeologia e la letteratura, per citare soltanto alcuni esempi. La statistica matematica si avvale di una vasta gamma di metodi di analisi e di misura: dalle misure della tendenza centrale e della dispersione, all'analisi dei sistemi complessi e delle decisioni razionali da prendere in riferimento a essi, attraverso lo studio delle forme delle distribuzioni, delle misure di correlazione, del campionamento, della significatività delle differenze osservate, della varianza, della covarianza e della regressione. Alle misure si richiedono proprietà diverse a seconda dei casi: le ipotesi che giustificano l'impiego del metodo semplice dei minimi quadrati non sono sempre valide; non lo sono, per esempio, quando si tratti di operare su un sistema generale di relazioni interdipendenti. Questo richiamo alle ipotesi prova che spesso, e forse di norma, lo statistico non sa quale sia il miglior metodo da adottare, anche perché nella scelta deve tenere sempre presente il rapporto tra i costi e i vantaggi connessi all'applicazione di metodi più sofisticati, che, se da un lato lasciano sperare in risultati migliori, dall'altro sono di certo più costosi.

Quanto abbiamo detto è sufficiente a far comprendere come la statistica sia una disciplina caratterizzata da una vasta area di applicazioni; saremo dunque costretti, anche limitandoci a illustrarne soltanto gli sviluppi più moderni, a operare una severa selezione degli argomenti da trattare. Ci limiteremo quindi a prendere in esame i problemi statistici relativi al campo delle scienze sociali, ivi inclusa naturalmente l'economia. In questo ambito considereremo gli sforzi più recenti compiuti per dare sistematicità alle statistiche economiche, sociodemografiche e dell'ambiente; analizzeremo però varie metodologie che trovano applicazione non soltanto in questi, ma anche in molti altri campi d'indagine.

2. Economia, società e ambiente

Alla luce degli avvenimenti che si sono verificati negli ultimi vent'anni, appare abbastanza chiaro che condizione per comprendere i problemi della società è la conoscenza del comportamento economico, dei processi sociali e delle condizioni ambientali. Questa conoscenza dipende dalla possibilità di disporre, in ciascuno di questi tre campi, di una solida base di dati statistici e dalla nostra capacità di stabilire tra essi delle connessioni. Comportamento economico, processi sociali e condizioni ambientali sono quindi per noi i tre pilastri, di importanza più o meno uguale, su cui dovrebbe reggersi un'analisi soddisfacente dei problemi delle società umane, anche se lo sviluppo dei sistemi statistici in questi tre campi di ricerca non è proceduto con pari rapidità.

Nella seconda metà del sec. XVII nacque in Gran Bretagna una nuova disciplina: l'aritmetica politica. Questa disciplina, che M.G. Kendall (v., 1960) considera come la vera precorritrice della statistica moderna, si sviluppò per merito di studiosi come Petty, Graunt, King e Davenant, il cui interesse era rivolto agli effetti sociali della politica dello Stato. Sebbene a quel tempo le fonti di dati fossero molto più povere di quanto lo siano attualmente, questi studiosi si sforzarono di raccogliere e ordinare il materiale necessario per i loro studi: fecero così la loro apparizione stime relative all'economia, alle condizioni sociodemografiche e all'ambiente. Alcuni di questi lavori hanno un tono sorprendentemente moderno: Deane e Cole (v., 1962) hanno dimostrato che le stime di grandezze economiche effettuate nel 1696 da King (v., 1936) per il 1688 possono essere riesposte sotto forma di cinque conti di bilancio del tipo cui ci si è abituati in quest'ultima generazione; lo stesso si può dire per la tavola di mortalità di Graunt (v., 1662), che è fra le più antiche, se non la più antica, e anticipa le moderne tavole di sopravvivenza.

Nei tre secoli che ci separano dagli aritmetici politici la quantità di dati statistici riguardanti la società e i suoi problemi si è accresciuta enormemente. Non c'è dubbio che, specialmente in epoca recente, siano stati compiuti i più grandi sforzi per elaborare e sistematizzare i dati economici. I sistemi di contabilità economica nazionale costruiti negli ultimi decenni sono stati elaborati nell'intento di dare una base alla politica economica. Sarebbe quindi auspicabile che essi non presentassero discontinuità nell'informazione, che il sistema di definizioni e i criteri di classificazione adottati fossero uniformi, che i dati raccolti fossero coerenti e tali da soddisfare le identità aritmetiche e contabili e inoltre abbastanza disaggregati e abbondanti da dare solido fondamento a modelli accettabili dei processi economici. Sono stati fatti notevoli progressi verso l'attuazione di questi modelli ideali, ma a tutt'oggi non si può dire che esista un paese ove il processo di perfezionamento sia giunto al termine.

3. Economia: il sistema dei conti nazionali

Risale agli anni trenta la tendenza a perfezionare le statistiche economiche e a organizzarle in un sistema di conti. Questa tendenza ricevette un forte impulso, almeno in Gran Bretagna, dalla politica seguita, in larga misura sotto la guida di Keynes, nell'affrontare i problemi della finanza di guerra, e divenne generale durante il periodo della ricostruzione postbellica. Da allora in poi hanno svolto un ruolo importante in questo processo due organizzazioni internazionali - l'Organizzazione Europea per la Cooperazione Economica e le Nazioni Unite - che hanno proposto sistemi di conti standardizzati nel duplice intento di fornire ai paesi membri criteri generali, dettati dall'esperienza, di perfezionamento dei loro conti nazionali, e di rendere più omogenei e confrontabili i sistemi di conti di paesi differenti. Si deve a Stone (v., 1963) una rassegna breve, ma abbastanza completa e documentata, relativa a questa fase, che va dalla fine degli anni trenta agli inizi degli anni sessanta.

I sistemi proposti in origine dalle due organizzazioni - OECE (v., 1950 e 1958), ora OCSE, e Nazioni Unite (v. U.N., Statistical Office, 1953) - non erano mai stati molto diversi e vennero resi quasi del tutto omogenei con una serie di revisioni effettuate tra il 1953 e il 1964. Tuttavia queste revisioni non previdero mai l'ampliamento dello schema originario, cosicché divenne sempre più difficile inserire e integrare nei due sistemi le molte nuove forme di statistiche economiche emerse in campi come l'analisi delle interdipendenze strutturali (input-output), dei flussi di fondi e dei bilanci nazionali e settoriali. Di conseguenza, nel 1964 l'Ufficio Statistico delle Nazioni Unite intraprese un lavoro di ampliamento del sistema dei conti nazionali, di norma abbreviato in SNA (System of National Accounts). Dopo un ampio dibattito condotto in ogni parte del mondo, le Nazioni Unite pubblicarono (v. U. N., Statistical Office, A system..., 1968) un nuovo e più ampio sistema di conti.

L'intento di coloro che avevano elaborato il nuovo SNA non era stato di cambiare le linee generali dello SNA originario, ma piuttosto di rielaborarne la struttura. Tuttavia, come è spiegato nella pubblicazione delle Nazioni Unite (ibid., pp. 14-16), alcuni dei problemi in discussione furono lasciati aperti con l'idea di riprenderli in considerazione in futuro. Si individuarono così tre gruppi distinti di problemi.

Il primo comprendeva i seguenti quattro argomenti sui quali si era già lavorato: a) bilanci nazionali e settoriali; b) stime a prezzi costanti; c) statistiche della distribuzione del reddito, del consumo e della ricchezza; d) elaborazione dettagliata di parti del sistema. Per quanto riguarda il punto a), mentre i bilanci sono già parte integrante del nuovo SNA, occorre ancora: 1) definire in modo esauriente i problemi concettuali cui essi danno luogo; 2) elaborare criteri generali di raccolta e sistemazione dei dati; 3) redigere bilanci tipo con le relative tavole. Per quanto concerne il punto b), il problema è stato affrontato nei suoi aspetti generali nella pubblicazione delle Nazioni Unite (ibid.), ma è necessario ancora: 1) elaborare criteri unificatori relativi a questioni particolari; 2) valutare i pro e i contro dei vari metodi e procedimenti alla luce delle esperienze accumulate in ogni parte del mondo; 3) collegare al sistema i tradizionali indici delle quantità e dei prezzi. Per quanto concerne il punto c), è in corso di elaborazione un sistema complementare di statistiche della distribuzione, di cui la versione più recente si trova in una pubblicazione delle Nazioni Unite edita nel 1977. Infine, per quanto riguarda il punto d), commissioni di specialisti delle Nazioni Unite stanno lavorando all'ulteriore elaborazione di alcuni settori del sistema, quali l'agricoltura, la sanità e l'istruzione, in modo da stabilire un legame tra lo SNA e le informazioni disaggregate riguardanti attività e settori specifici.

Il secondo gruppo si componeva di due argomenti al cui riguardo - al momento della pubblicazione - non si era andati oltre lo stadio delle discussioni preliminari: a) i conti regionali e b) i flussi e gli stock di capitale umano. Circa il primo punto, si prese atto che negli ultimi anni molti paesi si erano impegnati nell'elaborazione di conti regionali, ma si decise che, considerando i molti altri problemi sui quali era necessario lavorare ancora, non era il caso di attribuire importanza prioritaria all'obiettivo d'introdurre nello SNA una dimensione regionale. Circa il secondo punto, venne messa in rilievo la necessità di una più stretta integrazione fra statistiche sociali e demografiche e statistiche economiche, ma il problema fu alla fine accantonato e la sua soluzione rimandata. In realtà esso venne ripreso quasi immediatamente e i progressi finora compiuti verranno descritti più avanti nel cap. 6.

Anche il terzo gruppo si componeva di due argomenti sui quali la discussione fu piuttosto limitata: a) la classificazione funzionale degli inputs e b) la definizione di un preciso criterio di distinzione fra spese correnti e spese in conto capitale. Circa il punto a), si riconobbe che nelle fabbriche gli inputs primari e intermedi non sono usati soltanto per far fronte alle necessità essenziali della produzione, ma in parte servono per assicurare al personale determinati servizi, quali, per esempio, assistenza medica e attrezzature ricreative, e in parte sono destinati al settore della ricerca e dello sviluppo, da cui è difficile potersi attendere un contributo alla produzione corrente; si decise comunque di rimandare il problema a una fase successiva. Circa il punto b), si indicarono tre problemi principali: 1) l'opportunità di considerare la spesa per beni di consumo durevoli, come la spesa in beni capitali; 2) il riesame del modo di trattare la spesa per la ricerca e lo sviluppo; 3) il problema di un modo corretto di considerare alcune spese, come quelle per l'istruzione, al momento trattate interamente come spese correnti. Si finì tuttavia per lasciare immutati i metodi e i procedimenti esistenti.

Perciò, quando si arrivò alla formulazione definitiva del nuovo SNA, ci si rese conto del fatto che numerosi problemi, di cui molti erano ben consapevoli, non avevano avuto soluzione. Eppure questi problemi sono particolarmente importanti per gli obiettivi che in origine si intendeva conseguire con la creazione dei sistemi di conti nazionali: la costruzione di modelli econometrici e l'attuazione di una politica economica.

La maggior parte degli economisti è perfettamente consapevole di quanto sia difficile anche solo definire il benessere, per non parlare dei problemi che insorgono qualora si voglia determinarne il grado e la misura. Eppure, probabilmente, essi preferirebbero che nel loro paese il reddito nazionale, o il prodotto nazionale lordo pro capite, fosse elevato e crescente a ritmo costante, piuttosto che basso e stagnante o fluttuante. In altri termini, tendono ad attribuire un qualche valore di misura del benessere agli indici fondamentali che esprimono i risultati conseguiti dall'economia a livello aggregato e che figurano nei conti nazionali. Essi potrebbero giustificare il loro modo di vedere sostenendo che non esiste un nesso ovvio tra livello di sviluppo economico e uguaglianza sociale e che i problemi dell'ambiente e la considerazione per la qualità della vita hanno acquistato importanza soltanto in tempi recenti, in parte come conseguenza dell'esplosione demografica e in parte a causa dell'alto livello dei consumi e dei mutamenti tecnologici che l'hanno reso possibile.

I tempi cambiano e un'eccezione al generale consenso di cui godono gli indicatori economici tradizionali, come il PNL (un'eccezione connessa al rilievo che oggi viene dato ai problemi della giustizia sociale e dell'ambiente), è rappresentata da alcuni studiosi che ritengono che molti aspetti del benessere umano sfuggano agli indicatori sunnominati. E chiaro che si tratta di critiche di portata e di natura molto diversa da quella dei problemi, di cui si è detto sopra, lasciati insoluti nella progettazione del nuovo SNA. Torneremo su questo argomento nel cap. 5, ma prima riteniamo importante fare una breve digressione su una questione di diversa natura.

4. Sistemi alternativi

La maggior parte dei paesi che elaborano conti nazionali fanno uso del modello fornito dallo SNA o di qualcosa di molto simile. I paesi comunisti però adottano un sistema diverso: il sistema dei bilanci della produzione materiale (Material Product System, di norma abbreviato in MPS). I due sistemi differiscono sotto diversi aspetti, di cui il più importante è forse quello relativo al problema di quali grandezze economiche includere nella voce ‛produzione'. Parlando in generale, nello SNA la voce produzione comprende tutti i beni e i servizi, a eccezione di quelli prodotti su scala familiare o per hobby, mentre nell'MPS comprende solo l'output dei prodotti materiali, cioè l'output dei beni e i servizi dei trasporti, delle comunicazioni e della distribuzione.

Fino a poco tempo fa si è fatta una notevole confusione circa le relazioni esistenti fra i due sistemi, che spesso venivano considerati irriducibilmente opposti l'uno all'altro. Recentemente, grazie agli sforzi compiuti da un gruppo di lavoro della Conferenza degli statistici europei, queste relazioni sono state in gran parte chiarite. In una pubblicazione delle Nazioni Unite (v. U.N., Statistical Office, 1971), il Consiglio per la mutua assistenza economica espone autorevolmente le norme metodologiche fondamentali seguite nella costruzione dell'MPS. Stone ha dimostrato, con l'aiuto di un esempio numerico semplificato, che la matrice contabile di entrambi i sistemi può essere derivata da una sola matrice contabile pre- e postmoltiplicando per matrici di raggruppamento alternative (v. Stone, Porównanie..., 1968). È perciò chiaro che il punto essenziale in discussione non è la correttezza o meno dell'uno o dell'altro sistema, ma la loro relativa utilità a fini di analisi e di politica economica nelle condizioni specifiche dei diversi paesi.

Árvay (v., 1969) espone la variante ungherese dell'MPS sotto forma di una matrice di forma simile a quella che appare nell'introduzione al nuovo SNA curata dalle Nazioni Unite (v. U.N., Statistical Office, A system..., 1968).

5. Benessere e sistema dei conti nazionali

Nel cap. 3 abbiamo visto il sistema dei conti nazionali come un sistema in continuo sviluppo, nel cui ambito vengono gradualmente coordinate e perfezionate le statistiche economiche. In molti paesi il prodotto nazionale lordo pro capite a prezzi costanti è aumentato un po' più rapidamente e con fluttuazioni un po' meno ampie nel periodo postbellico che nel periodo fra le due guerre. Sarebbe assurdo individuare la causa di questi miglioramenti nel fatto che le statistiche economiche sono più perfezionate o che le analisi basate su di esse sono più raffinate, ma, al tempo stesso, è difficile immaginare che questi mutamenti nel flusso di informazioni economiche non abbiano avuto alcuna importanza.

Le categorie analitiche usate in questo stadio di sviluppo della contabilità nazionale sono quelle ritenute valide per lo studio di sistemi economici altamente organizzati, in cui sono largamente sviluppati l'uso della moneta e la divisione del lavoro. Questo fatto può essere illustrato analizzando il concetto di produzione. Se iniziamo col dire che produzione significa creazione di beni e di servizi, dobbiamo domandarci quale possa essere il criterio distintivo, se tale criterio esiste, fra la produzione che tenteremmo di registrare nei conti nazionali e la produzione che non dovrebbe essere registrata; per esempio, dobbiamo contabilizzare il prodotto di coloro che hanno l'hobby del giardinaggio o i servizi delle casalinghe? Di norma si procede concentrandosi in prima istanza sui beni e sui servizi prodotti per la vendita e prendendo poi in considerazione, eccezionalmente, un limitato numero di altre voci. Fra le eccezioni più importanti figurano i servizi della pubblica amministrazione in settori quali l'istruzione e la sanità. Questi servizi non vengono prodotti per essere venduti, anche se a coloro che ne usufruiscono può venir richiesto di contribuire a sostenerne il costo; ma nella maggior parte dei paesi servizi simili possono essere acquistati, sono istituzionalizzati e non vi sono difficoltà a definirli e a valutarli in termini di costi. Al contrario, i servizi delle casalinghe e i beni e i servizi prodotti per hobby non sono contabilizzati, perché di norma non sono registrati e non hanno prezzo, sono molto diversificati e rappresentano infine aspetti non isolabili del complesso modo di essere e di vivere della gente.

Si tratta di convenzioni che non ostacolano, anzi facilitano il raggiungimento dell'obiettivo, se l'obiettivo è quello di studiare l'economia intesa come un intreccio di relazioni tra famiglie, istituzioni pubbliche e imprese; mentre ci sarebbe da guadagnare ben poco se le categorie della produzione e del consumo fossero estese per comprendervi altre entità vaste e imprecise. Tuttavia, se ci poniamo dal più ampio punto di vista del benessere umano e vogliamo considerare tutte le risorse che possono contribuire ad accrescerlo, le conclusioni sono diverse: è chiaro che le casalinghe danno un grande contributo alla produzione, anche se molto di ciò che esse producono non è facilmente valutabile e nemmeno definibile, e appare assurdo allora escludere il risultato della loro attività produttiva dalla produzione, soltanto perché il loro posto di lavoro è anche la loro casa.

Se allarghiamo la nostra prospettiva per includervi un sempre maggior numero di aspetti del problema del benessere, dobbiamo affrontare molte e diverse questioni, alcune vecchie e altre nuove. Ne daremo ora alcuni esempi.

In primo luogo, c'è la questione della misurazione e della valutazione dei servizi che non sono prodotti per la vendita, come quelli offerti da enti pubblici. La prassi generalmente seguita nella contabilità nazionale è quella di utilizzare come indice dell'output gli inputs ponderati con i rispettivi costi unitari relativi a un anno base. Dato che attualmente le nostre capacità di misura e di stima sono piuttosto limitate, questo è forse il miglior procedimento possibile, ma esso presenta l'ovvio inconveniente di rendere impossibile il confronto tra inputs e outputs sia rispetto al valore che rispetto alle variazioni nel corso del tempo.

In secondo luogo, esistono alcuni tipi di beni e di servizi che sono comunemente considerati come ‛spiacevoli necessità'. I vari studiosi non sono d'accordo nell'indicare quali beni e servizi debbano essere inclusi in questa categoria; alcune spese di questo tipo comunemente accettate dagli esperti sono comunque, per esempio, le spese per la difesa, per i pendolari e per il condizionamento d'aria. Questi beni andrebbero esclusi dal prodotto totale perché, si sostiene, non sono desiderati per se stessi, ma soltanto per difendersi da circostanze esterne mutevoli.

Per quanto possa essere utile, nel caso di studi specifici riguardanti argomenti particolari, escludere queste voci dal concetto di produzione, il farlo sistematicamente non ci sembra un modo di procedere raccomandabile. Ciò non soltanto perché spesso gli individui e anche le comunità effettuano queste spese in conseguenza di una qualche scelta, ma anche perché nella vita quasi tutte le attività presentano i loro lati negativi che, se evidenziati di proposito, potrebbero essere usati come argomento a sostegno della loro esclusione dal concetto di produzione. Si potrebbe così sostenere che è un peccato che gli esseri umani siano fatti in modo da aver bisogno di mangiare regolarmente, cosa che comporta la fatica e la spesa di produrre e distribuire i cibi, di portarli a casa, cucinarli e infine mangiarli per poi lavare i piatti; oppure si potrebbe sostenere che è un peccato che gli esseri umani, a differenza di altri esseri impellicciati o pennuti, sentano la necessità di indossare degli abiti, o che si ammalino e abbiano così bisogno di cure mediche; o che alcuni di essi siano turbolenti e aggressivi rendendo così necessarie istituzioni per la difesa della legge e dell'ordine. Procedendo su questa strada potremmo pareggiare i conti nazionali mettendo uno zero su entrambi i lati, ma questi conti non riguarderebbero più il mondo in cui viviamo, bensì un mondo immaginario, popolato da creature mitiche tutte virtualmente, se non di fatto, morte.

Nel costruire un sistema di conti nazionali è bene pertanto evitare la riduzione arbitraria del concetto di produzione. Ciò non vuol affatto dire che, nel progettare una città nuova o nel rimodellarne una vecchia, non si debba fare tutto il possibile per minimizzare le ‛necessità spiacevoli', quali appunto il traffico pendolare o gli impianti di aria condizionata; in breve, per non perpetuare nel futuro gli errori commessi nel passato.

In terzo luogo, l'importanza che è venuta assumendo negli ultimi anni la tematica dell'ambiente ha posto agli studiosi della contabilità nazionale un gran numero di problemi. Secondo le convenzioni al momento attuale generalmente accolte, si contabilizzano i beni creati dal sistema di produzione, ma non gli scarti dei processi produttivi, come i materiali inquinanti e i rifiuti, a meno che non siano ricidati dall'azienda interessata o da enti pubblici. Anche quando sia effettuato il riciclaggio, il che non è la norma, questi prodotti non vengono contabilizzati in modo omogeneo: gli inputs richiesti dalle imprese per il riciclaggio sono considerati come beni intermedi, mentre gli inputs richiesti da enti pubblici sono considerati come beni finali. Questi diversi metodi di registrazione si riflettono in maniera diversa sui valori unitari nonché sulle variazioni nel tempo del prodotto finale.

Leontief (v., 1970) ha dimostrato che, disponendo di informazioni sull'emissione di prodotti inquinanti nei differenti rami di produzione e sulle strutture degli inputs dei processi capaci di eliminarli, è possibile effettuare una contabilizzazione completa dei vantaggi e dei danni entro uno schema allargato input-output. Occorre soltanto aggiungere un appropriato numero di righe e di colonne per i processi produttivi o le attività attraverso cui si riducono o si eliminano i prodotti inquinanti. Sulle righe aggiunte figurano le quantità dei vari prodotti inquinanti eliminati nei diversi rami di produzione, mentre le colonne aggiunte danno la struttura degli inputs impiegati nelle attività antinquinamento. Stone ha ampliato quest'analisi; infatti egli: 1) tratta esplicitamente la questione della misura ottimale di riduzione dell'inquinamento, tenendo conto che maggiore è la quantità di risorse destinata alla riduzione dei danni, minore sarà la quantità di risorse disponibile per la produzione di beni; 2) dà un'indicazione delle diverse conseguenze che si hanno sulla misura dei prezzi e sull'andamento della produzione, a seconda che si considerino i servizi antinquinamento come beni intermedi oppure come beni finali (v. Stone, The evaluation..., 1972). Nello stesso anno Meade (v., 1972) ha riformulato il problema in modo da mettere in evidenza che quel che importa al consumatore non è tanto la riduzione della quantità di prodotti inquinanti, quanto il grado di pulizia dell'aria, della terra e dell'acqua, che ne consegue.

Alcuni autori vorrebbero andare oltre e tener conto delle trasformazioni prodotte dall'inquinamento, dall'accumulo dei rifiuti, dall'esaurimento delle risorse naturali e così via, sia nei casi in cui siano state prese delle contromisure, sia nei casi in cui non siano state prese contromisure. Questi autori ritengono che prima o poi si dovrà trovare un rimedio per arrestare il processo di deterioramento e che quindi sarebbe il caso di seguire l'evolversi della situazione in modo da avere sempre un quadro aggiornato e una cognizione precisa della dimensione del compito che si ha davanti. Tutto ciò diverrebbe possibile ampliando lo schema dei conti nazionali, e in una pubblicazione dell'OECE (v., 1971) si dimostra che i conti possono essere riorganizzati in modo tale da non dover rinunciare alle informazioni tradizionali per far luogo alle nuove.

La discussione circa la rilevanza delle misure in campo economico per la difesa e l'accrescimento del benessere non è un fatto nuovo, tuttavia essa si è ampliata negli ultimi anni in conseguenza della crescente importanza attribuita ai fattori sociali e ambientali. Il lavoro che gli statistici ufficiali di tutto il mondo sono ora chiamati a intraprendere in questo campo è nuovo, di vasta portata e difficile, e perché sia coronato da successo non si potrà che procedere lentamente rispettando una serie di pri orità pratiche; altrimenti si corre il rischio che vadano perdute, con le illusioni degli entusiasti, molte delle informazioni preziose, per quanto limitate, di cui disponiamo attualmente. L'entusiasmo è molto utile come stimolo a prendere coscienza dell'esistenza dei problemi, ma è molto meno utile allorquando si tenta di risolverli.

Lasciamo ora da parte per un momento l'economia e torniamo agli aspetti statistici della demografia sociale e dell'ambiente. In primo luogo tracceremo il quadro generale, poi passeremo a considerare alcuni dei problemi che s'incontrano nella realizzazione di questo complesso programma statistico.

6. Demografia sociale: verso un sistema di statistiche sociali e demografiche

Le Nazioni Unite pubblicarono alla fine del 1968 il sistema riveduto dei conti nazionali. Poco tempo dopo l'Ufficio Statistico delle Nazioni Unite cominciò a considerare la possibilità di sistematizzare le statistiche sociali e demografiche. Un primo documento di lavoro venne discusso da un gruppo di esperti riuniti a Ginevra nell'estate del 1970. Questo documento e gli scritti successivi, a esso connessi, furono discussi nei centri statistici regionali delle Nazioni Unite. Una versione riveduta, dal titolo Towards a system of social and demographic statistics, venne discussa dal suddetto gruppo di esperti nella primavera del 1973 e, con alcune ulteriori modifiche, pubblicata dalle Nazioni Unite (v. U. N., Statistical Office, 1975) come rapporto provvisorio sul livello raggiunto dal sistema di statistiche sociali e demografiche (di norma abbreviato in SSDS: System of Social and Demographic Statistics).

La caratteristica essenziale di ogni sistema è data dalla struttura delle interconnessioni; in questo caso tale struttura assume le seguenti forme.

1. Consideriamo, all'inizio di un dato periodo di tempo, una popolazione suddivisa in categorie, secondo vari criteri di classificazione; a ogni categoria apparterrà un determinato numero di individui, che, in generale, sarà diverso alla fine del periodo considerato a causa degli spostamenti fra le varie categorie (o stati) verificatisi durante l'intervallo di tempo considerato: gli individui dello stock iniziale possono sopravvivere, morire o emigrare, mentre gli individui dello stock finale possono essere i sopravviventi dello stock iniziale o i nuovi nati o gli immigrati.

2. Queste informazioni sociodemografiche circa la numerosità di gruppi d'individui classificati secondo vari criteri sono messe in relazione con informazioni di carattere economico relative alla produzione. Ai differenti possibili stati degli individui sono abbinati dei costi unitari: per esempio, se si classificano gli individui della popolazione considerata secondo la loro posizione scolastica, ciascun individuo può o appartenere a uno dei diversi indirizzi del sistema scolastico o esserne escluso; è allora possibile assegnare un costo a ogni presenza nei diversi indirizzi del sistema. Se la classificazione dei dati contabili corrisponde a quella dei dati demografici, allora i due sistemi possono essere collegati tra loro mediante le equazioni di quantità e di prezzo di un sistema di input-output aperto.

3. Le informazioni sociodemografiche sono messe in relazione anche con informazioni economiche riguardanti il consumo. In questo caso i dati demografici sono abbinati ai dati che esprimono i benefici unitari in denaro e in natura percepiti dagli individui appartenenti alle diverse categorie. Il metodo per stabilire la connessione è anche in questo caso lo stesso descritto nel precedente capoverso.

Illustriamo queste connessioni con un semplice esempio. Indichiamo con n il vettore di stock di una popolazione supposta in equilibrio stazionario, cioè composta dallo stesso numero di individui all'inizio e alla fine di un intervallo di tempo; indichiamo con b il vettore dei nuovi entrati (nati e immigrati) e indichiamo con S la matrice dei sopravviventi, nella quale gli individui presenti sia nello stock iniziale sia in quello finale sono classificati secondo il loro stato iniziale nelle colonne e secondo il loro stato finale nelle righe. Allora, poiché lo stock finale è costituito dai sopravviventi dello stock iniziale e dai nuovi entrati, possiamo scrivere

n≡Si+b, (1)

dove i è il vettore unitario (1, 1, ..., 1), cosicché Si indica il vettore i cui elementi sono le somme degli elementi delle righe di S.

Possiamo costruire una matrice dei coefficienti, supposta costante nel tempo, dividendo gli elementi di ciascuna colonna di S per il corrispondente elemento di n. Questi coefficienti sono di norma chiamati rapporti di transizione e la loro matrice, che indichiamo con C, è data da

C=Sí^-1, (2)

dove í^-1 indica l'inversa della matrice diagonale ricavata dal vettore n. Se sostituiamo l'espressione di S ricavata dalla (2) nella (1), otteniamo

perché íi≡n e I rappresenta la matrice unità. L'equazione (3) è identica nella forma all'equazione di quantità di un modello input-output aperto; in essa figura l'inversa (I−C)^-1, cioè la matrice che trasforma il vettore dei nuovi entrati nel vettore degli stati della popolazione.

Supponiamo di dover studiare un sistema scolastico, così che la maggior parte degli elementi di n sia associata a indirizzi del sistema d'istruzione. Consideriamo un vettore, chiamiamolo m, basato sulla stessa classificazione di n, i cui elementi siano costi unitari per l'istruzione sostenuti nell'intervallo di tempo tipo, diciamo un anno. Allora le spese globali per l'istruzione che in media un individuo, attualmente in una certa posizione scolastica, dovrà sostenere in futuro costituiscono gli elementi di un vettore, k, tale che

che è l'equazione di prezzo corrispondente alla (3). Combinando la (3) con la (4) possiamo vedere che

In altri termini, per un sistema in equilibrio stazionario che operi a costi unitari costanti, la spesa annuale per l'istruzione è uguale al costo totale sostenuto per istruire i nuovi entrati durante l'anno.

Finora abbiamo considerato il sistema come un sistema input-output basato su una matrice, C, di rapporti di transizione. Se possiamo definire gli stati del sistema in modo da considerare gli elementi di C come delle probabilità, allora possiamo interpretare la matrice inversa (I - C)^-1 come la matrice fondamentale di una catena di assorbimento di Markov e il processo come un processo di Markov. La condizione che permette quest'interpretazione è che ogni elemento c_jk di C, cioè la probabilità di spostarsi con un solo passo dallo stato k allo stato j, si applichi a tutti gli individui che si trovano nello stato k. Questo implica che il percorso attraverso il quale un individuo ha raggiunto lo stato k è irrilevante per il suo spostamento futuro.

Se la matrice C può essere interpretata come una matrice di probabilità, allora gli elementi dell'inversa (I−C)^-1 ci danno molte informazioni utili. In primo luogo, gli elementi della diagonale rappresentano il tempo medio che un individuo il quale stia per raggiungere unp stato può attendersi di restarvi; se l'intervallo di tempo è un anno, questo tempo medio sarà espresso in anni. In secondo luogo, l'elemento della riga j e della colonna k, che non sta sulla diagonale, rappresenta il tempo medio di permanenza nello stato j moltiplicato per la probabilità di passare dallo stato k allo stato j. In terzo luogo, la somma degli elementi della colonna k rappresenta la speranza di vita di un individuo che pervenga allo stato k. E, infine, consultando una tavola di sopravvivenza possiamo risalire all'età alla quale corrisponde tale speranza di vita, che è poi l'età alla quale gli individui in media raggiungeranno lo stato k.

Le ipotesi su cui si basa questo semplice esempio sono fortemente restrittive, ma, come ha dimostrato Stone (v., 1971; A Markovian..., 1972; Transition..., 1973) e come risulta da una pubblicazione delle Nazioni Unite (v. U.N., Statistical Office, 1975), in linea di principio queste restrizioni possono essere nella maggior parte rimosse, sebbene in pratica l'operazione possa risultare molto difficile.

Nelle situazioni reali si ha a che fare con popolazioni che non sono in equilibrio stazionario e in questo caso ci si presenterà spesso la necessità di proiettare il numero di individui che si troveranno nei vari stati a diverse scadenze future. Se definiamo l'operatore di ritardo, Λ, tramite l'equazione Λ^θn(τ)≡n(τ+θ), allora, nel caso non stazionario, dobbiamo sostituire la (3) con la

Λn=Cn+b, (6)

la quale mostra che il vettore di stock all'inizio dell'anno successivo è uguale al vettore di stock all'inizio dell'anno in corso, trasformato una volta dalla matrice C, più il vettore esogeno dei nuovi entrati nell'anno in corso. Applicando Λ alla (6) e sostituendo Λn con Cn+b, otteniamo

se procediamo in questo modo fino al tempo τ, otteniamo

abbiamo dato anche la notazione che compare nella seconda riga della (8) soltanto per renderne possibile il confronto con la (9) che segue. La prima riga dell'equazione (8) rappresenta il vettore di stock al tempo τ diviso in due componenti, la prima delle quali rappresenta i sopravviventi dall'inizio del periodo, mentre la seconda rappresenta i sopravviventi dei successivi nuovi entrati. Per valori di τ più grandi della durata della vita umana, C^τ è una matrice nulla e così scompare il primo termine del lato destro della (8).

Per poter applicare la (8) occorre stimare Λ^θb per θ=0, 1, ..., τ−1, ma non discuteremo qui le possibili fonti di queste stime. È anche necessario ipotizzare che C sia una matrice fissa, il che non è molto plausibile. Si possono tuttavia indicare dei metodi per proiettare gli elementi di C e, se indichiamo con Λ^βC il valore di questa matrice proiettato in un futuro anno β, allora non è difficile dimostrare (v. Stone, A Markovian..., 1972 e Transition..., 1973) che la (8) è sostituita dalla

dove

Questo ci permette di sostituire (I−C)^-1 con (I−Å)^-1, dove

e quindi di fare uso delle proiezioni di C e di calcolare un'inversa che ne tenga conto.

Il modello può essere modificato e generalizzato in vari modi. Per esempio, si può ammettere che una società non sia omogenea e che gruppi differenti possano avere differenti probabilità di transizione, come nel modello di mobilità-permanenza (mover-stayer model) introdotto da Blumen, Kogan e McCarthy (v., 1955): in esso si fa l'ipotesi che un gruppo non cambi il suo stato mentre l'altro gruppo lo cambia secondo una matrice di transizioni fisse. Inoltre, Stone ha ideato un esempio attinente al campo della salute, nel quale estende lo spazio degli stati determinando gli stati stessi secondo caratteristiche sia passate che presenti (v. Stone, Transition..., 1973). Le matrici di transizione che ne risultano tendono a divenire molto grandi, ma esse sono di un tipo speciale e l'inversa può essere calcolata combinando l'inversione di matrici diagonali con la moltiplicazione di matrici.

Il modello descritto è essenzialmente orientato verso il futuro: esso riguarda gli stati verso i quali è probabile che la gente si sposti. Formando una matrice di coefficienti basata sulle righe anziché sulle colonne di S, è possibile costruire un modello orientato verso il passato, che consideri gli stati dai quali è probabile che la gente provenga. Caratteristica abbastanza interessante di questo modello è che esso può anche essere visto come orientato verso il futuro considerando il movimento dei posti vacanti anziché il movimento della popolazione. Così ha fatto White (v., 1970) nel suo studio sulle gerarchie della Chiesa.

Sebbene, come ha messo in rilievo Bartholomew (v., 1967), siano state già realizzate alcune esperienze nell'applicazione ai processi sociali di modelli basati sulle catene di Markov, specialmente nei campi della mobilità dell'occupazione e della mobilità sociale, si dovrà studiare ancora molto prima di poter affermare di essere in grado di costruire modelli soddisfacenti di questi processi. Si possono individuare subito due problemi tecnici.

1. Si deve fare ogni sforzo possibile per assicurare che gli stati del sistema siano definiti in modo tale che i rapporti di transizione a essi relativi possano venir trattati come probabilità.

2. Poiché i dati disponibili per stimare queste probabilità sono normalmente lontani da quelli ideali, sorge il problema, analizzato a fondo da Lee, Judge e Zelluer (v., 1970), dell'uso ottimale dei dati disponibili per la stima.

Finora abbiamo descritto in termini molto generali alcune delle principali forme di interconnessione che il sistema di statistiche sociali e demografiche (SSDS) tende a stabilire. In teoria, lo schema statistico proposto potrebbe adattarsi a fornire una descrizione di rapporti umani comunque complessa, vale a dire che potremmo lasciare interagire un numero qualsiasi di classificazioni. In pratica, però, non possiamo farlo, perché gli stati diverrebbero in breve così numerosi che sarebbe impossibile organizzarli in qualche modo. È necessario perciò distinguere vari aspetti della vita umana che per molte indagini possono essere considerati separatamente dagli altri, stabilendo poi tra essi delle connessioni quando se ne presenti la necessità.

Come abbiamo visto, la struttura dell'SSDS è dinamica e mette in relazione gli stock all'inizio di un intervallo con gli stock all'inizio dell'intervallo successivo. Conseguentemente, i vari aspetti della vita umana sono detti sequenze, accentuandone così il carattere longitudinale. Per ogni sequenza si dà la relativa descrizione, si espone la serie dei dati desiderati, si dà un insieme di classificazioni, si suggeriscono altre possibili classificazioni utili e si propongono alcuni indicatori sociali.

Si possono distinguere le seguenti sequenze. La prima è una sequenza demografica generale che tratta la dimensione e la struttura della popolazione: nascite, morti e migrazioni. La seconda è una sequenza che riguarda la formazione della famiglia, le famiglie e i nuclei familiari. A questo punto sorge un nuovo problema: se le famiglie costituiscono le unità di una matrice di transizione, si rendono necessarie alcune regole per determinare un unico mutamento di stato conseguente a un qualsiasi cambiamento, comunque determinatosi, della loro composizione. Inoltre, a proposito di questa sequenza, sorgono una serie di questioni diverse, ma strettamente connesse tra loro, che riguardano: abitazioni e loro ambiente; tempo libero e attività ricreative; mobilità sociale; distribuzione del reddito, dei consumi, dell'accumulazione e della ricchezza; servizi relativi alla sicurezza e al benessere sociali. La terza sequenza riguarda le attività di apprendimento e i servizi scolastici; la quarta le attività a scopo di guadagno, le prestazioni di lavoro e le persone inattive. Queste ultime due sequenze possono essere combinate a formare quella che possiamo chiamare una sequenza attiva, perché tratta il processo che va dalla nascita alla morte in termini di apprendimento e di guadagno, che sono le attività principali della maggior parte delle persone durante quasi tutto il corso della loro esistenza. Infine, una quinta sequenza riguarda la salute e i servizi sanitari e una sesta concerne la delinquenza e comprende ordine pubblico, criminali e vittime.

Concentrandosi sulle statistiche di una singola sequenza, o sottosistema, del sistema complessivo si può dare soluzione a molti problemi che interessano la collettività in generale e in particolare gli uomini politici e i funzionari della pubblica amministrazione. Per esempio, in una società in lenta evoluzione, il metodo sopra descritto di proiettare il numero delle unità presenti nei vari rami di un sistema scolastico può funzionare abbastanza bene. D'altro lato, se siamo interessati a capire le cause per le quali alcuni ragazzi vanno bene e altri male a scuola, probabilmente avremo bisogno di dati che normalmente non figurano nelle statistiche sull'istruzione: dati riguardanti la classe sociale, le dimensioni della famiglia, la salute, la razza e la religione. Orr (v., 1972) e Tuck (v., 1974) hanno tentato di misurare l'effetto che hanno sul profitto scolastico alcuni fattori quali il sesso, la classe sociale, il grado attitudinale e il tipo di scuola secondaria.

Questa necessità di combinare classificazioni tratte da sequenze differenti, ma in modo non arbitrario e tale da evitare la già ricordata escalation delle combinazioni, solleva la questione di come raccogliere le informazioni. È difficile, se non impossibile, raccoglierle su base rigida, regolare e codificata presso enti come le scuole e gli ospedali, oppure per mezzo di questionari obbligatori riempiti direttamente dalle singole persone, come in un censimento della popolazione. E per questa ragione che si sente sempre più l'esigenza di inchieste a carattere generale per campioni di famiglie.

In molti casi, quando si devono classificare gli individui in base a caratteristiche passate e presenti, è necessario, come abbiamo già rilevato, disporre di informazioni longitudinali che ci consentano lo studio di una particolare annata (o coorte). Un'interessante rassegna degli studi longitudinali nel campo delle scienze sociali si trova in Wall e Williams (v., 1970) e una rassegna dei più recenti sviluppi dello studio delle coorti è apparsa in U.K. Office of Population Censuses and Surveys (v., 1973).

Merita un accenno un'ultima questione connessa con l'SSDS: si sta lavorando allo sviluppo di un metodo che prevede l'uso del tempo come unità di misura e della tecnica dei bilanci temporali come mezzo per raccogliere le informazioni. Sulla scia di Tomlinson e altri (v., 1971) si è delineato un modello di distribuzione del tempo basato sui principî della meccanica statistica. Si dovrà tuttavia lavorare ancora molto prima di poter affermare di essere riusciti a integrare questa informazione nel resto del sistema.

Da questa rassegna relativamente breve risulta che gli statistici avranno molto lavoro da fare prima di darci un SSDS piano e ben articolato che possa essere confrontato con lo SNA, che a sua volta non è affatto perfetto. La raccolta di dati sui flussi, l'uso di nuovi metodi di raccolta, la stima dei parametri, il controllo di modelli alternativi dei processi sociali sono problemi che presentano tutti degli aspetti interessanti per il futuro. Comunque, in questo campo, il lavoro di sistematizzazione è andato più avanti che non nel campo delle statistiche dell'ambiente, il terzo pilastro dell'analisi sociale, al quale ora ci volgeremo.

7. L'ambiente: un futuro sistema di statistiche dell'ambiente?

In molti paesi sono disponibili, spesso in forma cartografica anziché statistica, informazioni relative a determinati aspetti dell'ambiente. In particolare, in molti paesi sono state condotte indagini sull'uso del territorio e si dispone di dati concernenti vari aspetti del sistema dei trasporti, l'approvvigionamento idrico e le abitazioni; tuttavia mancano in genere informazioni complete e significative sull'inquinamento. Attualmente in parecchi paesi si stanno compiendo sforzi per raccogliere dati al riguardo e in questo contesto possiamo fare riferimento al lavoro di Leontief e Ford (v., 1972), in cui gli autori danno alcune stime delle emissioni di cinque fonti d'inquinamento atmosferico per ognuna delle novanta industrie statunitensi da loro considerate.

Come abbiamo visto, nell'SSDS alle statistiche dell'ambiente si dà uno spazio limitato e le si considera in rapporto a quelle relative alle abitazioni e alle attrezzature disponibili per le attività del tempo libero. A suo tempo si discusse il problema se nell'SSDS si dovessero o meno inserire tutti i tipi di statistiche dell'ambiente, ma alla fine si decise di fare di queste statistiche l'oggetto di un lavoro a parte. Le ragioni principali di questa decisione furono, in primo luogo, il fatto che l'SSDS copre già un campo molto vasto, anche se ragionevolmente omogeneo, e, in secondo luogo, che le statistiche dell'ambiente sono qualcosa di diverso dalle statistiche sociali e demografiche e pongono differenti problemi di raccolta e di analisi.

Di conseguenza si assiste alla nascita di un sistema di statistiche dell'ambiente che si affianca agli altri due, anche se è ancora troppo presto per dire quale forma esso assumerà.

8. Problemi di applicazione

Ciò che abbiamo illustrato finora è un immenso programma di sistematizzazione e perfezionamento delle statistiche relative alle scienze sociali, alla politica sociale e all'amministrazione pubblica. I tre sistemi principali e le loro componenti devono essere caratterizzati da un alto grado di interconnessione; si riferiscono a processi dinamici e in essi assumono grande rilevanza le questioni della controllabilità e del controllo. Quali che siano i risultati che col nostro lavoro scientifico potremo raggiungere in questo campo, dobbiamo prendere atto del fatto che i processi sociali, per quanto concerne la loro conoscibilità, sono stocastici, perché l'incertezza è un dato ineliminabile nella maggior parte dei casi in cui occorre prendere delle decisioni.

Nel considerare i problemi di applicazione pratica di questi sistemi statistici conviene assumere come punto di riferimento gli obiettivi fondamentali cui essi tendono. Il primo obiettivo è di stabilire dei criteri generali che i singoli paesi possano utilizzare per sviluppare i loro sistemi statistici. E cosa riconosciuta che gli ordini di priorità sono diversi nelle diverse parti del mondo, che gli ordinamenti istituzionali sono anch'essi diversi e che il perfezionamento delle statistiche costa tempo e denaro. Perciò non dobbiamo aspettarci che si possa arrivare alla completezza e all'uniformità in un breve periodo. Può tuttavia essere utile disporre di un elenco di serie statistiche, su cui vi sia accordo generale, con le quali ogni paese possa confrontare le statistiche che effettivamente raccoglie; come pure è utile che vi sia uno schema di collegamento, completo di definizioni e classificazioni, entro cui si possano sistemare i dati provenienti dalle varie parti del mondo.

Nella misura in cui si metteranno in pratica queste raccomandazioni sarà possibile realizzare un secondo obiettivo, cioè la pubblicazione di dati confrontabili per il maggior numero possibile di paesi. Questo secondo obiettivo è importante per due ragioni: ci consente di vedere molti problemi su scala mondiale e non nell'ambito limitato della situazione di un solo paese; rende possibili analisi in crosssection basate su dati nazionali, analisi che con tutte le loro difficoltà costituiscono un potente strumento di studio della variabilità dei fenomeni sociali.

Il perfezionamento delle statistiche sarà probabilmente un processo lento che forse potrà essere accelerato se si considereranno più attentamente mezzi e fini. Spesso è possibile raccogliere nuove informazioni modificando metodi esistenti già speri mentati e accettati; se si può fare, tanto meglio. Inoltre, nuove informazioni raccolte per uno scopo specifico dovrebbero dimostrarsi utili per quello scopo; di qui l'elaborazione, nella delineazione dell'SSDS, di modelli semplici che indicano come si potrebbero usare le nuove informazioni per dare soluzione a problemi d'importanza generale. Naturalmente questi modelli non costituiscono l'ultima parola sull'argomento, anzi, in generale, sono soltanto la prima parola, ma bastano a dimostrare che in teoria i dati che ci si propone di raccogliere possono servire allo scopo per cui si suppone possano servire: se si raccolgono i dati, si possono risolvere determinati problemi. I modelli possono non essere adatti, ma senza dato non si vede come potrebbero essere migliorati. Non importa se si parte dalla teoria o dalle osservazioni empiriche, purché poi si passi dall'una alle altre e viceversa.

Questa discussione porta a chiedersi se nel progettare un sistema si debba partire da principi generali oppure dall'esigenza concreta di risolvere problemi specifici. Sembra chiaro, posto che il sistema possa trattare problemi specifici, che esso dovrebbe basarsi su principi generali, perché in tal caso è più probabile che i dati raccolti in base a esso siano utili anche per la soluzione di altri problemi. Un esempio può essere tratto dall'economia. Lo SNA originale (1953) si basava quasi completamente su principi generali: si deve distinguere fra transazioni correnti e operazioni in conto capitale; i conti devono essere in pareggio; le somme delle voci componenti devono essere uguali ai totali aggregati. Nello SNA riveduto (1968) s'introdussero molte altre considerazioni riguardanti specifiche forme di analisi, come, per esempio, l'analisi delle interdipendenze strutturali (input-output) del sistema produttivo, che poterono essere incorporate senza difficoltà nello schema originario. Fin qui abbiamo considerato i dati statistici riguardanti le scienze sociali e la loro sistematizzazione. Ora dobbiamo rivolgere l'attenzione ai vari aspetti della metodologia statistica.

9. Classificazione, raggruppamento e aggregazione

Le classificazioni, di cui sopra abbiamo dato alcuni esempi, sono importanti in tutti i campi di studio. In termini generali, si è in presenza di un certo numero di elementi ognuno dei quali possiede una serie di attributi o caratteristiche. Il nostro compito consiste nel costruire, in base a tutte queste informazioni, un insieme di categorie, tra le quali si possano ripartire gli oggetti della ricerca secondo un criterio significativo. La significatività dipende dagli scopi per i quali si effettua la classificazione. Per esempio, la classificazione internazionale standard dell'industria (v. U.N., Statistical Office, International..., 1968), che riguarda le aziende che producono beni e servizi, è una classificazione gerarchica a quattro livelli: le unità produttive sono raggruppate in sottoclassi, le sottoclassi in classi, le classi in rami e i rami in settori. Questa classificazione ha soprattutto lo scopo di raggruppare le unità produttive in categorie omogenee rispetto alla gamma dei prodotti. Per stabilire l'omogeneità di più prodotti si può fare riferimento, applicando due criteri ovvi anche se contrastanti, o all'uso cui sono destinati o al tipo di processo produttivo che richiedono. Per esempio, uno stabilimento tessile appartiene al settore ‛manifatturiero' e al ramo dell'industria tessile, dell'abbigliamento e del cuoio; fa parte della classe ‛industria tessile' e della sottoclasse ‛filatura, tessitura e finissaggio'. In contrasto con questa classificazione, la maggior parte dei lavori di riparazione (eccezion fatta per la riparazione di navi) è compresa nel settore dei servizi sociali e personali anziché nel settore manifatturiero.

Le unità rilevate possono essere classificate e ripartite fra le varie categorie in vari modi, che dipendono dal grado di formalizzazione del processo di classificazione, da quanto sono esplicite le caratteristiche cui si fa riferimento e dalla forma della funzione che esprime il criterio di classificazione scelto. È probabile che, per la maggior parte, le classificazioni standard attualmente in uso si debbano al lavoro di una singola persona o di un piccolo gruppo di persone e che siano state gradualmente perfezionate senza ricorrere tanto a metodi formali, quanto piuttosto alle conoscenze e all'esperienza. Nel caso delle imprese industriali, è necessario apportare cambiamenti ai criteri di classificazione ogniqualvolta appaiono nuove tecniche e nuovi prodotti. Per motivi diversi, si potrebbe dire lo stesso per altre classificazioni.

Mentre continuano a fiorire metodi informali, si sono fatti dei tentativi, almeno a partire dagli anni venti, per sviluppare metodi formalizzati, come ha fatto per es. Mahalanobis (v., 1927), il cui contributo ha condotto al concetto di distanza generalizzata e alla sua misurazione. La rassegna delle classificazioni, dovuta a Cormack (v., 1971), mette in evidenza la varietà degli obiettivi e dei criteri che sono stati proposti come base per una classificazione formalizzata. Si deve a Jardine e Sibson (v., 1971) una rassegna dettagliata dei problemi e dei procedimenti di tassonomia matematica, illustrata da esempi relativi a numerosi campi di indagine; Sibson (v., 1972) ha anche dimostrato l'importanza dei metodi a ordine invariante.

L'analisi dei raggruppamenti (cluster analysis) consiste nel tentare di assegnare gli oggetti d'indagine a diversi gruppi in modo tale che gli elementi di un gruppo siano simili tra loro, ma dissimili dagli elementi appartenenti ad altri gruppi. Com'è stato sottolineato da Rao (v., 1952), in questo tipo di analisi s'incontrano molte difficoltà: può essere essenziale standardizzare e normalizzare in vario modo le misure e tener conto delle correlazioni esistenti fra di esse; inoltre i procedimenti da seguire per la formazione dei gruppi variano a seconda che si vogliano formare gruppi semplici, anelli o catene.

Stone (v., 1960), in un lavoro di economia in cui applica l'analisi dei raggruppamenti, ci dà un esempio di questo tipo di difficoltà. Il problema è quello di formare con le dodici regioni statistiche della Gran Bretagna dei gruppi semplici, basati su un insieme di transazioni a livello altamente aggregato volte a riflettere la struttura economica delle regioni stesse. Stone applica molte varianti del metodo considerato, effettuando i relativi calcoli, e ottiene risultati molto simili, che s'accordano in larga misura con le aspettative. Un'applicazione di questo metodo ai rapporti esistenti fra la delinquenza e un certo numero di variabili economiche e sociali è esposta succintamente in un lavoro di M. Flynn, P. Flynn e N. Mellor (v., 1972).

Le analisi di Orr (v., 1972) sulla carriera scolastica, cui si è già fatto riferimento, prendono le mosse da un campione di studenti di cui si considerano diverse caratteristiche: sesso, classe sociale, tipo di scuola secondaria frequentata e così via. Il passaggio da un punto all'altro dell'iter scolastico è analizzato in termini di una gerarchia stratificata di dicotomie. La prima dicotomia viene stabilita in base alla caratteristica rispetto alla quale la proporzione di transizione presenta una variabilità maggiore che non rispetto a qualsiasi altra caratteristica dicotomica. Le seconde dicotomie vengono stabilite ognuna in riferimento a quella caratteristica che spiega la maggior parte della variabilità, e così via. La tecnica usata per arrivare a questi risultati è descritta da Sonquist e Morgan (v., 1964) e i relativi risultati possono venir esposti nella forma di un albero (reticolo semplicemente connesso) o dendrogramma del tipo illustrato da Sibson (v., 1972).

Raggruppando le unità in classi si ottengono degli aggregati statistici: per esempio, raccogliendo dati su inputs e outputs delle aziende, è possibile costruire una tavola input-output per rami di produzione. Possiamo quindi domandarci se si perderebbe molto, oltre naturalmente alle informazioni dettagliate presenti nel materiale disaggregato, raggruppando i rami di produzione come abbiamo in precedenza raggruppato le singole aziende; e possiamo chiederci se esista un metodo di raggruppamento che preservi meglio di altri le informazioni contenute nel materiale non raggruppato. Possiamo osservare che questi interrogativi sono simili a quelli che sorgono quando si vogliano classificare elementi costituiti da gruppi già formati anziché da singole unità.

Si tratta di un problema che ha una sua influenza su molti aspetti della vita economica. Nel campo del comportamento del consumatore è stato discusso da Hicks (v., 1937 e 1939) e in riferimento alle relazioni input-output e ad altri rapporti economici da Theil (v., 1954) e da Malinvaud (v., 1955 e 1956). Se ne può trovare un'interessante trattazione in un lavoro di W. D. Fisher (v., 1969).

L'aggregazione è importante per i modelli basati sulle catene di Markov (v. cap. 6), perché, come hanno dimostrato Kemeny e Snell (v., 1960), gli stati di una matrice di Markov non possono, salvo in casi speciali, essere aggregati in modo da produrre una matrice di Markov più piccola.

10. Coerenza, aggiustamento delle osservazioni e aggiornamento

Nel costruire un sistema di statistiche economiche e sociali si incontrano di norma problemi di coerenza, intesi nel significato ordinario del termine. I dati di base raramente sono omogenei e completi. Un aggregato, come, per esempio, il prodotto nazionale lordo, spesso può essere stimato in base a statistiche del reddito, della produzione o della spesa, e le tre stime possono non coincidere. Il risparmio, sebbene sia di norma stimato come eccesso del reddito sulla spesa, può anche essere stimato come variazione dell'eccesso delle attività sulle passività tenuto conto dei trasferimenti di capitale, e di nuovo le stime possono non coincidere. Ciò significa che il costruttore di modelli che voglia avvalersi di tutti i dati disponibili deve affrontare il problema di ricavare da tali dati un complesso di stime coerente.

In linea di principio si tratta di un problema analogo a quello tipico delle scienze naturali, vale a dire l'aggiustamento delle stime per depurarle dagli errori di misura. Se si misura più volte una lunghezza, oppure un angolo, ci si accorgerà che le diverse misure non coincidono perfettamente e se si misurano i tre angoli di un triangolo si troverà che la loro somma non raggiunge esattamente i 180°. Si richiede quindi uno strumento di aggiustamento delle singole misure che consenta di ottenere stime non distorte, le quali, nel caso del triangolo, soddisfino due tipi di condizioni: 1) ogni stima corretta deve avere un unico valore; 2) la somma delle tre stime corrette deve essere identicamente uguale a 180°.

Potremmo presentare in questa forma anche esempi tratti dalle scienze sociali, tuttavia in pratica i due casi sono differenti. Nell'esempio del triangolo, le misurazioni possono essere ripetute e si può quindi ottenere una misura obiettiva dell'errore, ma il problema tipico nel campo delle scienze sociali è proprio che le misurazioni, di norma, non possono essere ripetute. In queste circostanze, il metodo dell'aggiustamento, sebbene inevitabilmente basato su stime soggettive dell'errore, è meglio che niente, specialmente se le stime sono effettuate dai compilatori stessi.

Se per il momento trascuriamo la questione di come calcolare gli errori, il problema può essere formulato nei termini seguenti. Consideriamo un vettore x* (del tipo ν×1) di stime iniziali, che contiene stime non distorte di un altro vettore, cioè il vettore dei valori veri, x. Supponiamo che gli elementi di x siano soggetti a μ vincoli lineari, cioè che sia

Gx=h, (12)

dove G è del tipo μ×ν e di rango μ e h è del tipo μ×1. Indichiamo con V* la matrice, di ordine ν e di rango maggiore di μ, della varianza degli elementi di x* e supponiamo che ogni vincolo soddisfatto da x* sia linearmente indipendente dalla (12). Allora la migliore stima lineare non distorta x** di x è data da

x**=x*−V*G′(GV*G′)^-1(Gx*−h), (13)

da cui si può vedere che gli elementi di V* devono soltanto essere approssimati a meno di un fattore di proporzionalità, poiché ogni fattore di questo tipo scomparirà nel prodotto di matrici V*G′(GV*G′)^-1. La matrice della varianza di x**, indicata con V**, è

V**=V*−V*G′(GV*G′)^-1GV*. (14)

Le stime finali che soddisfano tutti i vincoli sono date dagli elementi di x** (eq. 13) e la matrice della varianza di queste stime, V** (eq. 14), differisce da V* in quanto tiene conto dei vincoli del sistema come pure delle impressioni iniziali dell'investigatore.

È spesso possibile dividere i vincoli in due insiemi, aggiustare le stime iniziali in modo che soddisfino uno degli insiemi e procedere poi all'aggiustamento delle stime già parzialmente corrette in modo che soddisfino il secondo insieme di vincoli. Il vantaggio di questo procedimento a due stadi consiste nel fatto che esso rende possibile effettuare i calcoli separatamente, cosicché la più grande matrice da invertire è di ordine uguale al numero dei vincoli compresi nell'insieme maggiore.

Per applicare questo metodo sono necessarie due cose: uno strumento per valutare le varianze e le covarianze delle stime iniziali, che sono gli elementi di V*, e uno strumento per scomporre il problema in parti, in modo da evitare le immense matrici che si formerebbero se, ad esempio, tentassimo di aggiustare con un'unica operazione un insieme particolareggiato di conti nazionali.

Per quanto riguarda il problema degli errori, possiamo cominciare dall'ipotesi che sia V*=λΙ (dove, come abbiamo visto, il fattore di proporzionalità λ non ha effetto sui risultati), per poi vedere come questa ipotesi possa essere modificata. Essa implica che le stime iniziali siano indipendenti fra loro, non distorte e con varianza uguale; il che equivale a dire che potremmo correggere ciascuna di esse indipendentemente dalle altre mediante l'aggiunta o la sottrazione di una quantità fissa al fine di equilibrare l'intero sistema.

Poiché probabilmente gli elementi del sistema sono di grandezza notevolmente diversa, potrebbe essere preferibile l'ipotesi che gli errori standard anziché essere tutti uguali siano proporzionali alle stime iniziali. Ma si può andare anche oltre, perché coloro che curano le statistiche sanno che alcune delle loro stime hanno basi solide, mentre altre sono poco più che congetture. Perciò potrebbe essere plausibile aumentare alcune stime dell'errore e ridurne altre rispetto all'errore standard corrispondente all'ipotesi di proporzionalità, anche se neppure l'entità degli aumenti e delle riduzioni potrebbe essere precisa. Infine, considerando le fonti e i metodi di stima applicati, si può dedurre qualcosa circa le intercorrelazioni esistenti fra gli errori di stima. Circa la questione della scomposizione del sistema da correggere in un certo numero di parti di dimensioni più maneggevoli, abbiamo già visto che in molti casi è possibile scomporre l'insieme dei vincoli. Ma ciò non basta e la strategia più promettente sembrerebbe essere la seguente: prima si riduce, per aggregazione, il sistema grande a un sistema piccolo e poi, dopo aver corretto gli elementi del sistema piccolo, si adattano le componenti di questi aggregati ai loro totali.

Il metodo sopra delineato venne proposto da Stone, Champernowne e Meade (v., 1942) come un metodo di aggiustamento dei sistemi di conti nazionali. Sebbene di tanto in tanto tale metodo sia stato applicato a esempi limitati appositamente costruiti, esso non è stato finora accolto da coloro i quali curano le statistiche economiche, anche se, con l'estendersi delle stime dirette, con lo sviluppo dei modelli econometrici e con l'uso sempre più diffuso dei calcolatori, in alcuni istituti statistici esso va conquistandosi un favore maggiore rispetto a una generazione fa.

Stone ha applicato il metodo al problema della proiezione delle tavole input-output nel caso in cui le stime dei prezzi e delle quantità vengano effettuate separatamente (v. Stone, Input-output..., 1968). Questo però non è il problema di aggiustamento che si presenta di norma in relazione all'aggiornamento e alla proiezione di tavole input-output. Il problema nella sua forma consueta consiste nell'aggiustare una matrice nota di coefficienti input-output, in modo che soddisfi i vettori marginali noti di una matrice di flussi di prodotti intermedi per un periodo differente, rispettando i vincoli rappresentati dal vettore noto dei prodotti lordi; si tratta cioè di un metodo di aggiustamento biproporzionale. I metodi biproporzionali sono stati usati per lungo tempo per adattare dati campionari ai totali dei censimenti, come hanno fatto Deming e Stephan (v., 1940) e dopo di loro Friedlander (v., 1961). Quello usato di norma per aggiustare tavole input-output, il metodo RAS, è stato delineato da Stone (v., Multiple..., 1962), sviluppato da Bates e Bacharach (v., 1963) e poi ampiamente analizzato e illustrato ancora da Bacharach (v., 1970). Nell'ultimo decennio è stato applicato a una vasta gamma di problemi di aggiustamento in campo economico.

Il metodo RAS è il seguente: supponiamo di dover aggiornare una matrice dell'anno base, espressa in prezzi dell'anno base, trasformandola in una matrice dell'anno in corso, espressa in prezzi correnti. Indichiamo con u, v, q i vettori relativi all'anno in corso rispettivamente dell'output intermedio, dell'input intermedio e dell'output totale e indichiamo con A la matrice dei coefficienti input-output sempre dell'anno in corso. Allora

Aq=u (15)

æA′i=v. (16)

All'inizio A è incognita, ma abbiamo una matrice nota, A*, ottenuta rivalutando gli elementi della matrice dell'anno base ai prezzi correnti. Usiamo A* per effettuare una stima iniziale, chiamiamola u₀, di u. Si avrà allora

A*q=u₀. (17)

In generale u₀≠u, perciò il passo successivo è costruire un'uguaglianza moltiplicando appropriatamente le righe di A*:

ûû₀^-1A*q=u. (18)

Le condizioni relative alle righe (eq. 15) sono ora soddisfatte, mentre non lo sono le condizioni relative alle colonne (eq. 16); si può fare in modo che lo siano sostituendo nella (16), al posto di A, la sua espressione ricavata dalla (18) e moltiplicando appropriatamente le colonne di A. Si avrà allora

æA*′ûû−₀¹i=v₀ (19)

e

ævv−₀¹A*′ûû−₀¹i=v. (20)

Se continuiamo così, dopo n volte avremo

Le condizioni per la convergenza di questo processo, illustrate da Bacharach (v., 1970), sono soddisfatte nelle applicazioni pratiche: al crescere di n, u_n→u e v_n→v e quindi, per n sufficientemente grande, il termine fra parentesi nella (21) può essere considerato come una stima di A. Così

A=ré*A*sé*, (22)

dove r*=λr e s*=λ^-1s, essendo λ una costante arbitraria. Dai simboli usati nella (22) si capisce perché questo procedimento venga denominato metodo RAS.

I vettori r e s possono essere interpretati come segue. Se coloro che fanno uso di un dato prodotto variassero tutti il loro consumo di una stessa percentuale per unità di produzione, allora A sarebbe uguale a réA*; d'altra parte, se in ciascun ramo della produzione variasse la quantità di inputs primari immessi nel processo produttivo in combinazione con la quantità iniziale di inputs intermedi, allora A sarebbe uguale ad A*sé. Le variazioni del prodotto intermedio sono date dalla (22) in una forma da cui risulta che esse possono essere espresse come combinazione dei due effetti.

Sebbene in molte circostanze questo metodo possa fornire una buona approssimazione, è facile constatare che non sempre esso dà risultati attendibili. Per esempio, nell'ultimo decennio, l'impiego del carbone come combustibile si è andato riducendo e si è preferito usare al suo posto il petrolio e il gas. Tale riduzione non è stata uniforme in tutte le industrie e questa potrebbe essere una considerazione secondaria; esiste però un problema più serio: c e un settore della produzione, l'industria del coke, in cui il carbone entra come materia prima anziché come combustibile e in questo caso l'input per unità di prodotto non è affatto diminuito. Il basso valore del coefficiente r del carbone riduce il coefficiente d'impiego del carbone nell'industria del coke, ma, poiché si tratta di una materia prima di cui si fa un uso massiccio e per la quale l'input necessario alla produzione non è affatto diminuito, il coefficiente s del coke dovra essere elevato per compensare l'errore indotto dal basso valore del coefficiente r. Tuttavia, poiché è improbabile che l'alto valore del coefficiente s sia corretto, il risultato delle ipotesi indebitamente semplici del modello è di disseminare di errori la matrice A stimata. Questo esempio dimostra come non ci si possa attendere che con un metodo di aggiustamento così semplice si possano trattare tutti i complessi problemi dell'evoluzione dell'industria e che esso dovrebbe essere usato come ultima risorsa soltanto se fallissero gli sforzi per ottenere informazioni dirette sulle variazioni dei singoli coefficienti. In tal caso questo metodo può svolgere un utile ruolo.

11. Identificazione, sistemi e stima

Il problema dell'identificazione, come viene comunemente definito, è da lungo tempo ben noto agli economisti. L'esempio classico è dato dalle relazioni fra offerta e domanda: la quantità offerta è, in generale, una funzione crescente del prezzo e la quantità richiesta è, in generale, una funzione decrescente del prezzo. In queste circostanze, che cosa può dedursi, ad esempio, da serie temporali del prezzo e della quantità comprata e venduta di una merce? A questa domanda diede risposta Working (v., 1927), dimostrando che, se variassero i fattori diversi dal prezzo che influenzano l'offerta, mentre i fattori che influenzano la domanda non subiscono alcuna variazione, la dispersione dei punti genererebbe una curva di domanda, e viceversa. Tuttavia, fu soltanto molto più tardi che, con Haavelmo (v., 1943), vennero formalmente enunciate le implicazioni statistiche dei sistemi di equazioni simultanee. Prima di descrivere la situazione di cui si occupò Haavelmo, consideriamo l'identificazione nei termini statistici più semplici. Supponiamo di avere un'equazione di regressione che metta in relazione x e y, ciascuna misurata dalla propria media, della forma

y=βx+u, (23)

dove β è un parametro e u un vettore delle perturbazioni. Supponiamo inoltre che sia

u=αx+e, (24)

dove α è un parametro ed e un vettore delle perturbazioni distribuito in modo indipendente da x con media zero e varianza σ². Se sostituiamo nella (23) u con la sua espressione ricavata dalla (24), otteniamo

y=(α+β)x+e. (25)

In queste circostanze, una regressione coi minimi quadrati di y su x ci dà una stima non distorta di α+β ma non fornisce alcuna informazione su β. In questo caso si dice che β non è identificato. Haavelmo (v., 1943) ha dimostrato che questa situazione s'incontra necessariamente, a meno che non si facciano ipotesi particolari, quando si tenta di stimare i parametri di un sistema di equazioni simultanee, come risulta dal seguente semplice esempio.

Siano y₁, y₂ e y₃ i vettori rispettivamente della quantità richiesta, della quantità offerta e del prezzo di una merce. Consideriamo il seguente modello di domanda e offerta:

y₁=α₁₃y₃+u₁ (26)

y₂=α₂₃y₃+u₂ (27)

y₁=y₂, (28)

dove α₁₃ e α₂₃ indicano rispettivamente un parametro della domanda e un parametro dell'offerta, u₁ e u₂ sono vettori di perturbazioni e ciascuna variabile è misurata dalla sua media. Se isoliamo l'equazione di domanda (26), la stima di α₁₃ secondo il metodo dei minimi quadrati, chiamiamola α*₁₃, è data da

α*₁₃=y1′y₃/y3′y₃. (29)

Se premoltiplichiamo la (26) per y3′, dividiamo per lo scalare y3′y₃ e prendiamo i valori medi, otteniamo

y1′y₃/y3′y₃=α₁₃+ε(u1′y₃/y3′y₃). (30)

L'espressione a sinistra della (30) è uguale ad α*₁₃ e può essere uguale ad α₁₃ soltanto se ε(u1′y₃/y3′y₃)=0, cosa che si verifica se y₃ e u₁ sono distribuiti indipendentemente. Ma in generale ciò non può verificarsi, perché, per la (28), possiamo eguagliare le espressioni a destra della (26) e della (27), ottenendo

y₃=(u₁−u₂)/(α₂₃−α₁₃), (31)

cosicché sarebbe necessario che u₁ e u₁−u₂ fossero distribuiti indipendentemente, condizione questa che imporrebbe severe restrizioni alla distribuzione congiunta di u₁ e u₂.

Vi sono diversi modi di uscire da questo vicolo cieco.

In primo luogo, potremmo disporre di qualche informazione sulla variabilità relativa di u₁ e u₂. Nel caso estremo in cui è u₁={0, 0, ..., 0}, mentre gli elementi di u₂ presentano una considerevole variabilità, i valori dei dati osservati giaceranno sulla curva di domanda e saremo in grado di stimare α₁₃, ma non α₂₃. In un caso meno estremo, in cui gli elementi di u₁ variano molto poco rispetto a quelli di u₂, la stima di regressione, sebbene distorta, si approssimerà a una stima di α₁₃. Questo è in sostanza il genere di situazione affrontato da Working (v., 1927). In casi più complessi, come quelli considerati da Koopmans (v., 1949), potrebbe essere utile imporre qualche vincolo alla distribuzione congiunta di u₁ e u₂.

In secondo luogo, potremmo discutere la specificazione del modello costituito dalle (26), (27) e (28), considerando che l'offerta corrente probabilmente dipende dai prezzi dell'anno precedente, anziché dai prezzi correnti, a causa del ritardo, che si verifica ad esempio in agricoltura, fra la decisione di produrre e l'effettiva produzione di un dato bene. Se sostituiamo y₃ nella (27) con Λ^-1y₃, cioè con il suo valore dell'anno precedente, possiamo stimare ora α₂₃ e, uguagliando l'espressione a destra della (26) alla nuova versione del secondo membro della (27), possiamo stimare α₂₃/α₁₃ e conseguentemente α₁₃. Questo è un semplice esempio di sistema ricorsivo, termine introdotto da Bentzel e Wold (v., 1946), nel quale la simultaneità delle cause dà luogo a una sequenza di cause e i parametri strutturali possono essere stimati in un ordine definito.

In terzo luogo, come avremmo dovuto fare sin dall'inizio, potremmo riconoscere che vi sono altre variabili oltre il prezzo che influenzano sia la domanda che l'offerta. Introduciamo due variabili che tratteremo come esogene: il reddito dei consumatori, x₁, dal lato della domanda, e la piovosità, x₂, dal lato dell'offerta. Allora possiamo sostituire il modello semplice con

y₁=α₁₃y₃+β₁₁x₁+u₁ (32)

y₂=α₂₃y₃+β₂₂x₂+u₂ (33)

y₁=y₂, (34)

oppure, se sostituiamo l'espressione di y₂ ricavata dalla (34) nella (33),

in forma compatta si ha

YA=XB+U, (36)

da cui, se A è non singolare,

dove C≡BA^-1; la (37) si chiama forma ridotta del sistema originale. In termini dei singoli parametri strutturali,

da cui: α₁₃=c₂₁/c₂₂; α₂₃=c₁₁/c₁₂; β₁₁=(c₁₁c₂₂−c₁₂c₂₁)/c₂₂; β₂₂=(c₁₂c₂₁−c₁₁c₂₂)/c₁₂. Gli elementi di C possono essere stimati applicando una regressione basata sui minimi quadrati alle singole equazioni della (37), perciò, dato che è β₁₁≠0 e β₂₂≠0, i quattro parametri strutturali possono essere calcolati univocamente dalle stime di regressi one; in altre parole, i quattro parametri nel modello allargato, dato dalla (32), dalla (33) e dalla (34), sono identificati.

I due modelli finora considerati illustrano casi estremi: il primo rappresenta un sistema completamente non identificato e il secondo un sistema completamente identificato. Questi non sono tuttavia i soli due casi: come si può facilmente dimostrare, un modello può essere sottoidentificato o sovraidentificato.

Supponiamo di sopprimere il termine in x₁ nella (32). Allora la matrice C, corrispondente alla (38), prende la forma

dalla quale possiamo ottenere una stima valida di α₁₃ ma non di α₂₃ o di β₂₂. In altre parole è identificata l'equazione della domanda, ma non l'equazione dell'offerta.

Infine, supposto di aver soppresso il termine in x₁ dalla (32), aggiungiamo un termine alla (33) in una nuova variabile esogena, x₃. In questo caso la matrice C prende la forma

Come nella (39), α₁₃ è di nuovo il solo parametro strutturale che può essere calcolato dalle stime di regressione; ma in questo caso può essere calcolato due volte, una volta dalla prima riga e una volta dalla seconda riga della (40). Non vi è ragione perché queste due stime siano uguali e in questo caso l'equazione della domanda è sovraidentificata, mentre l'equazione dell'offerta resta non identificata.

Che cosa si può fare se si presenta uno di questi casi? Consideriamo tre possibilità.

1. Se il sistema di equazioni che abbiamo costituito è completamente identificato sembrerebbe che tutto sia chiaro; tuttavia, vi sono due possibili difficoltà che dobbiamo tenere presenti. Prima: se alcune delle variabili supposte predeterminate sono variabili casuali, la cui misura è soggetta a errore, esse non saranno in generale distribuite indipendentemente dalle perturbazioni e quindi le stime che entrano nei nostri calcoli, al contrario dei loro veri valori, non possono propriamente venir considerate come predeterminate. Seconda difficoltà: le variabili determinanti che figurano nelle equazioni trasformate, le (37) di cui sopra, in tali equazioni devono essere distribuite indipendentemente dalle perturbazioni e queste dipendono a loro volta dalle perturbazioni che figurano in molte equazioni originali, se non in tutte. In pratica questa condizione è probabilmente troppo restrittiva.

2. Problema della sovraidentificazione. I metodi per trattare questo problema vennero sviluppati negli anni quaranta e possono trovarsi nei lavori curati da Koopmans (v., 1950) e da Hood e Koopmans (v., 1953). Questi metodi il metodo dei minimi quadrati con informazione limitata e il metodo di massima verosimiglianza con informazione completa - sono alquanto complicati e qui non li considereremo. Del resto, almeno per campioni grandi, si possono ottenere risultati simili con il più semplice metodo dei minimi quadrati a due stadi, che può essere illustrato nel seguente modo. Supponiamo di avere un sistema di due equazioni,

nel quale tutte le variabili esogene sono nella (41). Se effettuiamo la regressione di y₁ su x₁ e x₂, otteniamo le seguenti stime contrassegnate con gli asterischi:

y*₁=β*₁₁x₁+β*₁₂x₂. (43)

Questo è il primo stadio. Ora, se effettuiamo la regressione di y₂ su y*₁ otteniamo

y*₂=α*₂₁y*₁. (44)

Questo è il secondo stadio. Il metodo è descritto da Theil (v., 1958 e 1971) e permette di ottenere una stima di α₂₁ che è coerente e non affetta da distorsione, come sarebbe se si ricavasse col metodo dei minimi quadrati semplici.

Sebbene non riguardi direttamente il problema dell'identificazione, vogliamo qui accennare a un teorema dimostrato da Frisch e Waugh (v., 1933), secondo il quale non fa alcuna differenza, per quanto concerne i risultati, che la regressione coi minimi quadrati sia basata su deviazioni da trends lineari oppure che un termine con trend lineare venga aggiunto all'insieme originario di variabili. Questo teorema può essere generalizzato, come ha dimostrato Stone; ciò apre un altro campo di applicazione per il metodo dei minimi quadrati a due stadi (v. Stone, Uogolnienie..., 1962).

Un'altra possibilità, nel caso in esame, è quella di minimizzare, rispetto ai parametri strutturali, la somma dei quadrati non spiegata dalla regressione. La matrice C, per la (41) e la (42), può essere scritta nella forma

dove y₁=α₂₁, y₂=β₁₁/(1−α₁₂α₂₁) e y₃=β₁₂/(1−α₁₂α₂₁), e per stimare i γ si può applicare una tecnica di stima non lineare, come fa Marquardt (v., 1963).

Ciò condurrà a una stima unica di α₂₁; non si può far nulla per α₁₂, β₁₁ e β₁₂, tranne che stimare il rapporto β₁₁/β₁₂, cosa che, in qualche caso, può essere utile. Un metodo generale per trattare problemi non lineari in econometria è illustrato da Goldfeld e Quandt (v., 1972).

3. Il caso della sottoidentificazione è un caso in cui non si può fare molto, perchè, per quanto grande sia il numero delle osservazioni, è impossibile stimare parametri che non possono essere identificati. Abbiamo accennato alla possibilità d'incorporare nel modello vincoli imposti alla distribuzione congiunta delle perturbazioni, ma in pratica ciò non sarebbe facile. Un'altra possibilità, illustrata da H. R. Fisher (v., 1966), consiste nel basare la scelta di un insieme accettabile di valori dei parametri su restrizioni ragionevoli che si suppone essi possano soddisfare. Nel caso considerato da Fisher, la gamma dei valori accettabili era notevolmente ristretta, ma non ci si può attendere che ciò si verifichi nella generalità dei casi.

Sebbene sia possibile formulare in teoria le condizioni per l'identificazione, non ne consegue che si sappia come procedere in pratica. Nel caso di modelli piccoli, come quelli illustrati sopra, si tratta soltanto di ricavare algebricamente la matrice C, ma nel caso di modelli grandi ciò è praticamente impossibile. Uno studio approfondito di questo argomento si trova in un'opera di F. M. Fisher (v., 1966), ma il problema continua ad assorbire l'attenzione degli econometrici ed è probabile che sarà così ancora per molti anni.

12. Previsioni e proiezioni

Se fosse possibile rappresentare una parte del mondo reale per mezzo di un modello deterministico dinamico completo, con parametri esattamente noti e immutabili, le previsioni sarebbero relativamente semplici. Questa possibilità è così lontana dalla realtà che diviene importante indagare come e quanto la nostra capacità di previsione risenta di limiti di vario genere e vedere che cosa si può fare, eventualmente, per migliorare la situazione.

Iniziamo con una singola equazione stocastica nella quale una variabile dipendente è in relazione lineare con un insieme di variabili esogene linearmente indipendenti, che sono distribuite congiuntamente indipendentemente da un termine di errore con media zero e varianza σ². Questa equazione può essere scritta nella forma

y=Xb+e, (46)

dove y indica un vettore di osservazioni della variabile dipendente, le colonne della matrice X contengono corrispondenti osservazioni di ciascuna delle variabili esogene, b indica un vettore di parametri ed e un vettore di errori. Allora la stima di b secondo il metodo dei minimi quadrati, chiamiamola b*, è

b*=(X′X)^-1X′y. (47)

Supponiamo ora di voler prevedere il valore che y assumerà in un qualche periodo futuro τ. Se indichiamo il valore previsto con y*_τ, allora si avrà

dove X_τ′ indica un vettore riga dei valori delle variabili esogene nel periodo τ. Il corrispondente valore effettivo, y_τ, è

dove e_τ indica l'errore effettivo nel periodo τ. La differenza, y_τ−y*_τ, è

ed è facile dimostrare, come è stato fatto nel lavoro di Stone e altri (v., 1954), che la varianza dell'errore di previsione, ε(y_τ−y*_τ)², è

Dalla (50) risulta che, anche se potessimo prevedere con esattezza i valori delle variabili esogene nel periodo τ (gli elementi del vettore X_τ′), vi sarebbero ancora due fattori che entrerebbero nell'errore di previsione: 1) la differenza, b−b*, fra i valori effettivi dei parametri e le nostre stime; 2) l'errore, e_τ, al quale è soggetta l'equazione effettiva nel periodo τ. Dalla (51) si ricava che il rapporto tra la varianza dell'errore di previsione e la varianza dell'errore dell'equazione, cioè σ², è [X_τ′(X′X)^-1X_τ+1].

Supponiamo ora che gli elementi di e siano autocorrelati e, in particolare, che sia

e=Λ^-1e+f; (52)

gli elementi di f hanno media zero e varianza σ². Se indichiamo con Δ*≡(1−Λ^-1) l'operatore a ritroso delle differenze prime e applichiamo questo operatore alla (46), otteniamo

Δ*y=Δ*Xb+f (53)

e così possiamo evitare i problemi associati agli errori autocorrelati sostituendo a y e X, Δ*y e Δ*X.

Data la (52), la (53) costituisce uno strumento valido per stimare b e σ² e, se la usiamo per prevedere un periodo successivo al periodo iniziale 0, otteniamo, corrispondentemente alla (50),

y₁−y*₁=(X1′−X0′(b−b*)+f₁; (54)

mentre se la usiamo per previsioni relative a τ periodi dopo il periodo iniziale, otteniamo

Se confrontiamo i secondi termini sul lato destro della (50) e della (55), possiamo vedere che, mentre nella (50) è σ² che contribuisce alla varianza dell'errore di previsione, nella (55) questo contributo diviene τσ². In altre parole, nella (55) questa varianza cresce col tempo, mentre ciò non si verifica nella (50). Questa circostanza non costituisce un motivo per abbandonare la (53) quale equazione stimante, perché, se vale la (52), la (46) non vale più.

Se sostituiamo la (52) con la

e=αΛ^-1e+f, (56)

dove 0≤α〈1, allora, come hanno dimostrato Stone e Prais (v., 1953), τσ² basato sulla (55) è sostituito da

e, quando α→0, la varianza →σ². Ciò era prevedibile, poiché, se è α=0, allora si ha e=f e si torna alla (46).

Certamente conviene, e probabilmente è in molti casi giustificabile, rappresentare i termini di errore come nella (52). Tuttavia, ciò implica un'ipotesi molto particolare e, anche se non ricorriamo a qualcosa di più complicato della (56), resta il problema di decidere circa il valore di α. In generale, non vi è ragione perché non vi siano parecchi termini ritardati nella (56), ciascuno col suo coefficiente da stimare, sebbene sia dubbio, dato il numero di osservazioni normalmente disponibili nell'analisi delle serie temporali, che sia possibile determinare più di due, o al massimo tre, di tali termini. Un metodo per effettuare tali stime è stato proposto da Champernowne (v., 1948 e 1969).

L'ulteriore difficoltà, cui abbiamo già accennato, di dover prevedere le variabili esogene suggerisce che dovremmo esaminare le possibilità di sistemi di equazioni stocastiche lineari alle differenze finite, in cui le sole variabili predeterminate siano variabili endogene ritardate.

Le variabili in tali sistemi possono essere organizzate in due forme diverse: la forma ridotta, nella quale i valori correnti delle variabili sono espressi in termini dei valori passati di ognuna delle variabili del sistema, e la forma autoregressiva, nella quale ogni variabile è espressa in termini dei propri valori passati. In entrambi i casi, in ciascuna delle equazioni appaiono termini di errore più o meno complicati. Un'interessante caratteristica dei sistemi lineari è che, a parte i termini di errore, tutte le equazioni nella forma autoregressiva sono identiche.

In base a tali equazioni è possibile calcolare la varianza delle previsioni, ivi incluso il valore finale di queste varianze se il processo continua indefinitamente. Stone (v., 1951) ha dimostrato che per l'equazione

y+α₁Λ^-1y+a₂Λ^-2y=e, (58)

nella quale gli elementi di e sono distribuiti indipendentemente con varianza σ², il rapporto, chiamiamolo ϕ, tra la varianza finale della previsione e σ² è dato da

Perciò ϕ è uguale a uno se α₁=α₂=0 e cresce da questo punto attorno ai contorni di un triangoloide, finché si approssima a ∞ sui bordi di un triangolo con vertici α₁=−2, α₂=1; α₁=2, α₂=1; α₁=0, α₂=−1. È stato suggerito che i parametri strutturali del sistema potrebbero essere stimati dalla forma ridotta, che in base a essi si potrebbero costruire le stime nella forma autoregressiva e che queste potrebbero essere usate per calcolare il valore di ϕ per ciascuna equazione. La conclusione che si possono fare previsioni soltanto per periodi futuri brevi, a meno che non sia possibile, in qualche modo, rendere le perturbazioni molto piccole, conferma un risultato cui pervenne molti anni fa Yule (v., 1927) a proposito del numero delle macchie solari: "Le perturbazioni che si verificano in ogni intervallo implicano un elemento di imprevedibilità che cresce molto rapidamente con il tempo".

Finora abbiamo parlato delle difficoltà che si incontrano nell'effettuare delle previsioni, ma ciò non significa che non si possano ottenere risultati positivi. L'esempio seguente, tratto da Stone (v., Personal..., 1973), riguarda le previsioni condizionali o proiezioni, come possiamo chiamarle, delle variazioni annuali della spesa pro capite per consumi privati in Gran Bretagna, valutata a prezzi costanti prendendo come base l'anno 1963. I dati erano disponibili per il periodo che va dal 1948-1949 al 1969-1970. Usando le informazioni relative ai primi diciotto anni, si stimarono le costanti di un'equazione di regressione lineare che vennero poi combinate con i valori delle variabili predeterminate, come apparivano nei dati iniziali, al fine di proiettare la variabile dipendente per i rimanenti quattro anni, dal 1966-1967 al 1969-1970. La serie dei valori calcolati era 5,57, 6,53, −0,23, 10,43, mentre la serie dei valori osservati era 5,64, 7,04, −0,55, 10,62. Le differenze, 0,07, 0,51, −0,32, 0,19 illustrano la (55), nell'ipotesi che i valori futuri delle variabili esogene, (X_τ′−X0′), siano noti. Naturalmente in pratica non lo sono e questo fatto spiega perché sia auspicabile lavorare con modelli completi. Inoltre è probabile che i dati riguardanti il passato siano soggetti a revisione e questo introdurrà ulteriori errori nelle previsioni in tempo reale.

Nel campo delle previsioni basate su serie temporali si presentano molti altri problemi ed esistono molti altri modi di affrontarli. Se le serie disponibili sono abbastanza lunghe, è possibile applicare i metodi dell'analisi spettrale illustrati da Granger e Hatanaka (v., 1964). Box e Jenkins (v., 1970) ci danno una succinta rassegna dei metodi disponibili per effettuare previsioni con modelli stocastici basati su serie temporali.

13. Politica, ottimizzazione e controllo

Di norma lo scopo delle previsioni è di formulare aspettative circa il futuro e di creare quindi la possibilità di prendere, se occorre, opportuni provvedimenti. In alcuni casi si costruiscono modelli di previsione indipendentemente da eventuali politiche che potrebbero essere adottate in base a essi, perché queste politiche non avrebbero un effetto apprezzabile sulle variabili considerate. Ad esempio, nel caso delle previsioni meteorologiche, più che di provvedimenti da prendere si può parlare di azioni da evitare, perché è difficile supporre che allo stato attuale delle conoscenze esista la possibilità di intervenire in qualche modo sulle condizioni del tempo. In altri casi, previsioni e politiche sono legate molto più strettamente, perché è probabile che cambiamenti di politica influenzerebbero proprio le variabili oggetto di previsione. In questi casi una previsione sfavorevole porterà a prendere misure intese a far sì che essa non si avveri. Ciò vale particolarmente per le scienze sociali. Per esempio, la gente era abituata a pensare che il livello della disoccupazione fosse un fenomeno simile al tempo e che non si potesse far nulla in proposito se non alleviare la condizione di miseria del disoccupato con sussidi di disoccupazione o altre forme di assistenza sociale. Oggigiorno agli uomini politici è affidato un compito più ambizioso: di fronte alla previsione di un alto livello di disoccupazione, essi non devono limitarsi a proporre dei palliativi, ma possono tentare, adottando una politica idonea, di far sì che le previsioni non si avverino. Naturalmente nell'elaborare una politica intesa a scongiurare la disoccupazione si deve tenere conto anche di altre grandezze economiche, come lo stato della bilancia dei pagamenti e il tasso di inflazione; ma queste sono complicazioni prevedibili e non escludono la possibilità di adottare una politica che raggiunga l'obiettivo prefissato.

Una teoria della politica economica legata a un modello econometrico di previsione fu sviluppata da Tinbergen (v., 1952 e 1956), che mise l'accento sulla necessità di specificare chiaramente gli obiettivi e sul fatto che il numero degli strumenti politici impiegati deve essere uguale al numero degli obiettivi, se s'intende conseguirli con una specifica regolazione degli strumenti. Questa linea generale di pensiero fu ampliata da Theil (v., 1964), il quale formulò le norme ottimali di decisione nell'intento di massimizzare una funzione quadratica di utilità soggetta a vincoli lineari. All'incirca nello stesso periodo si cominciò a considerare, come fecero Tustin (v., 1953) e Phillips (v., 1954-1958), la possibilità di applicare i metodi della progettazione dei sistemi di controllo alla regolamentazione dei sistemi economici; ne dà un esempio Livesey (v., 1971). Attualmente si stanno compiendo sforzi per integrare in questo campo le idee degli ingegneri e degli economisti.

Qui sorgono due nuovi problemi: 1) formulare una funzione di utilità accettabile; 2) escogitare un metodo agevole per calcolare i valori mutevoli che le variabili-strumento devono assumere al fine di massimizzare la funzione. Come avviene comunemente anche in altri campi, le opinioni divergono al momento di stabilire fino a che punto possa arrivare la formalizzazione dell'intero processo, specialmente quando si prende in considerazione il ruolo dell'incertezza. Anche se l'obiettivo finale è la formalizzazione completa, ci sono pur sempre da risolvere numerosi e difficili problemi, così che è quasi inevitabile partire da un metodo meno formalizzato che proceda per tentativi e si fondi sull'analisi di sensibilità.

14. Conclusioni

Come si è detto, nello stendere questo articolo non solo abbiamo operato una selezione drastica degli argomenti, ma abbiamo anche dovuto tralasciare molti aspetti degli argomenti che abbiamo trattato. Speriamo comunque di aver detto abbastanza per dare un'idea dell'immensa gamma di problemi che lo statistico deve affrontare nel campo delle scienze sociali: dai progetti di programmi per la raccolta di dati alla stima dei parametri dei sistemi di controllo ottimale. La generazione passata ha risolto molti problemi, ma molti altri restano in attesa di una soluzione che dovrà venire dalla prossima generazione (v. anche biometria, demografia, economia e popolazione).

bibliografia

Árvay, J., Development of the national accounting system in Hungary, in "The review of income and wealth", 1969, XV, pp. 185-195.

Bacharach, M., Biproportional matrices and input-output change, Cambridge 1970.

Bartholomew, D. J., Stochastic models for social processes, New York 1967.

Bates, J., Bacharach, M., Input-output relationships, 1954-1966, in A programme for growth, vol. III, London 1963, pp. VIII e 1-81.

Bentzel, R., Wold, H., On statistical demand analysis from the viewpoint of simultaneous equations, in ‟Skandinavisk Aktuarietidskrift", 1946, XXIX, pp. 95-114.

Blumen, I., Kogan, M., McCarthy, P. J., The industrial mobility of labor as a probability process, Ithaca 1955.

Box, G. E. P., Jenkins, G. M., Time series analysis, forecasting and control, San Francisco 1970.

Champernowne, D. G., Sampling theory applied to autoregressive sequences, in "Journal of the Royal Statistical Society", series B (methodological), 1948, X, pp. 204-231.

Champernowne, D. G., Estimation and uncertainty in economics, 3 voll., Edinburgh-London 1969.

Cormack, R. M., A review of classification (with discussion), in "Journal of the Royal Statistical Society", series (general), 1971, CXXXIV, pp. 321-367.

Deane, Ph., Cole, W. A., British economic growth 1688-1959, Cambridge 1962, 1967².

Deming, W. E., Stephan, F. F., On a least-squares adjustment of a sampled frequency table when the expected marginal totals are known, in "The annals of mathematical statistics", 1940, XI, pp. 427-444.

Fisher, F. M., The identification problem in econometrics, New York 1966.

Fisher, H. R., A unitary interpretation of Professor Stone's equations for savings and expenditure, in "L'industria", 1966, 4, pp. 500-509.

Fisher, R. A., Statistical methods for research workers, Edinburgh-London 1925.

Fisher, W. D., Clustering and aggregation in economics, Baltimore 1969.

Flynn, M., Flynn, P., Mellor, N., Social malaise research: a study in Liverpool, in "Social trends", H. M. S. O., 1972, pp. 42-52.

Friedlander, D., A technique for estimating a contingency table, given the marginal totals and some supplementary data, in "Journal of the Royal Statistical Society", series A (general), 1961, CXXIV, pp. 412-420.

Frisch, R., Waugh, Fr. V., Partial time regressions as compared with individual trends, in "Econometrica", 1933, I, pp. 387-401.

Goldfeld, S. M., Quandt, R. E., Nonlinear methods in econometrics, Amsterdam 1972.

Granger, C. W. J., Hatanaka, M., Spectral analysis of economic time series, Princeton 1964.

Graunt, J., Natural and political observations mentioned in a following index, and made upon the bills of mortality, London 1662.

Haavelmo, T., The statistical implications of a system of a simultaneous equations, in "Econometrica", 1943, XI, pp. 1-12.

Hicks, J. R., Théorie mathématique de la valeur en régime de libre concurrence, Paris 1937.

Hicks, J. R., Value and capital, Oxford 1939.

Hood, W. C., Koopmans, T. C. (a cura di), Studies in econometric method, New York 1953.

Jardine, N., Sibson, R., Mathematical taxonomy, New York 1971.

Kemeny, J. G., Snell, J. L., Finite Markov chains, Princeton 1960.

Kendall, M. G., Where shall the history of statistics begin?, in ‟Biometrika", 1960, XLVII, pp. 447-449.

King, G., Natural and political observations and conclusions upon the state and condition of England (1696), in Two tracts by Gregory King, Baltimore 1936, pp. 1-76.

Koopmans, T. C., Identification problems in economic model construction, in ‟Econometrica", 1949, XVII, pp. 125-144.

Koopmans, T. C. (a cura di), Statistical inference in dynamic economic models, New York 1950.

Lee, T. C., Judge, G. G., Zellner, A., Estimating the parameters of the Markov probability model from aggregate time series data, Amsterdam 1970.

Leontief, W., Environmental repercussions and the economic structure: an input-output approach, in A challenge to social scientists (a cura di Sh. Tsuru), Tokyo 1970, pp. 114-134.

Leontief, W., Ford, D., Air pollution and the economic structure: empirical results of input-output computations, in Input-output techniques, Amsterdam 1972.

Livesey, D. A., Optimising short-term economic policy, in "The economic journal", 1971, LXXXI, pp. 525-546.

Mahalanobis, P. C., Analysis of race mixture in Bengal, in "Journal and proceedings of the Asiatic society of Bengal", 1927, XXIII, pp. 301-333.

Malinvaud, E., Aggregation problems in input-output models, in The structural interdependence of the economy, New York 1955, pp. 189-202.

Malinvaud, E., L'agrégation dans les modèles économiques, in "Cahiers du séminaire d'économétrie", 1956, IV, pp. 69-146.

Marquardt, D. W., An algorithm for least squares estimation of nonlinear parameters, in "Journal of the Society of Industrial and Applied Mathematics", 1963, XI, pp. 431-441.

Meade, J. E., Citizens' demands for a clean environment, in "L'industria", 1972, 3-4, pp. 145-152.

OECE (Organizzazione Europea di Cooperazione Economica), A simplified system of national accounts, Paris 1950, 1951.

OECE (Organizzazione Europea di Cooperazione Economica), A standardised system of national accounts, Paris 1958.

OECE (Organizzazione Europea di Cooperazione Economica), Environment and growth in national accounts, in "DES/NI/70.3", 1971, pp. 1-31.

Orr, L., The dependence of transition proportions in the education system on observed social factors and school characteristics, in "Journal of the Royal Statistical Society", series A (general), 1972, CXXXV, pp. 74-95.

Phillips, A. W., Stabilisation policy in a closed economy, in "The economic journal", 1954, LXIV, pp. 290-323.

Phillips, A. W., Stabilisation policy and time-forms of lagged responses, in "The economic journal", 1957, LXVII, pp. 265-277.

Phillips, A. W., La cybernétique et le contrôle des systèmes économiques, in ‟Cahiers de l'Institut de Science Économique Appliquée", 1958, LXXII, pp. 41-48.

Rao, R. C., Advanced statistical methods in biometric research, New York-London 1952.

Sibson, R., Order invariant methods for data analysis (with discussion), in "Journal of the Royal Statistical Society", series B (methodological), 1972, XXXIV, pp. 311-349.

Sonquist, J. A., Morgan, J. N., The detection of interaction effects, Ann Arbor 1964.

Stone, R., Prediction from autoregressive schemes and linear stochastic difference systems, in Proceedings of the International Statistical Conferences 1947, Calcutta 1951, vol. V, pp. 29-38.

Stone, R., A comparison of the economic structure of regions based on the concept of distance, in "Journal of regional science", 1960, II, pp. 1-20.

Stone, R., Multiple classifications in social accounting, in "Bulletin de l'Institut International de Statistique", 1962, XXXIX, pp. 215-233.

Stone, R., Uogolnienie twierdzenia Frischa i Waugha, in "Przeglad Statystyczny", 1962, IX, pp. 401-403.

Stone, R., Contabilidad social y cuentas nacionales normalizadas, in "Información comercial española", 1963, CCLVI, pp. 31-39.

Stone, R., Mathematics in the social sciences and other essays, London 1966.

Stone, R., Input-output projections: consistent prices and quantity structures, in "L'industria", 1968, 2, pp. 212-224.

Stone, R., Porównanie systemów SNA i MPS, in Bilanse Gospodarski Narodowej, Warszawa 1968, pp. 283-307.

Stone, R., Mathematical models of the economy and other essays, London 1970.

Stone, R., Demographic accounting and model building, Paris 1971.

Stone, R., A Markovian education model and other examples linking social behaviour to the economy (with discussion), in "Journal of the Royal Statistical Society", series A (general), 1972, CXXXV, pp. 511-543.

Stone, R., The evaluation of pollution: balancing gains and losses, in "Minerva", 1972, X, pp. 412-425.

Stone, R., Personal spending and saving in post-war Britain, in Economic structure and development (a cura di H. C. Bos e altri), Amsterdam 1973, pp. 75-98.

Stone, R., Transition and admission models in social demography, in "Social science research", 1973, II, pp. 185-230.

Stone, R., Champernowne, D. G., Meade, J. E., The precision of national income estimates, in "The review of economic studies", 1942, IX, pp. 111-125.

Stone, R. e altri, The measurement of consumers' expenditure and behaviour in the United Kingdom, 1920-1938, vol. I, Cambridge 1954.

Stone, R., Prais, S. J., Forecasting from econometric equations: a further note on derationing, in "The economic journal", 1953, LXIII, pp. 189-195.

Theil, H., Linear aggregation of economic relations, Amsterdam 1954.

Theil, H., Economic forecasts and policy, Amsterdam 1958, 1961².

Theil, H., Optimal decision rules for government and industry, Amsterdam 1964.

Theil, H., Principles of econometrics, New York-Amsterdam 1971.

Tinbergen, J., On the theory of economic policy, Amsterdam 1952.

Tinbergen, J., Economic policy: principles and design, Amsterdam 1956.

Tomlinson, J. e altri, A model of daily activity patterns: development and sample results, in Land use and built forms studies, W. P. n. 43, Cambridge 1971, pp. 1-78.

Tuck, M. G., The effect of different factors on the level of academic achievement in England and Wales, in "Social science research", 1974, III, pp. 141-149.

Tustin, A., Economic regulation through control-system engineering, in "Impact of science on society", 1953, IV, pp. 83-110.

Tustin, A., The mechanism of economic systems, London 1953.

U. K. Office of Population Censuses and Surveys, Cohort studies: new developments. Studies on medical and population subjects, n. 25, H. M. S. O., London 1973.

U. N., Statistical Office, A system of national accounts and supporting tables. Studies in methods, series F, n. 2, New York 1953; rev. 1, New York 1960; rev. 2, New York 1964.

U. N., Statistical Office, A system of national accounts. Studies in methods, series F, n. 2, rev. 3, New York 1968.

U. N., Statistical Office, International standard industrial classification of all economic activities. Statistical papers, series M, n. 4, rev. 2, New York 1968.

U. N., Statistical Office, Basic principles of the system of balances of the national economy. Studies in methods, series F, n. 17, New York 1971.

U. N., Statistical Office, Towards a system of social and demographic statistics. Studies in methods, series F, n. 18, New York 1975.

U. N., Statistical Office, Provisional guidelines on statistics of the distribution of income, consumption and accumulation of households, in "Statistical papers", series M, 1977, LXI, pp. X e 1-97.

Wall, W. D., Williams, H. L., Longitudinal studies and the social sciences, London 1970.

White, H. C., Chains of opportunity, Cambridge, Mass., 1970.

Working, E. J., What do statistical ‛demand curves' show?, in "The quarterly journal of economics", 1927, XLI, pp. 212-235.

Yule, G. U., On a method of investigating periodicities in disturbed series, with special reference to Wolfer's sunspot numbers, in "Philosophical transactions of the Royal Society", series A, 1927, CCXXVI, pp. 267-298.