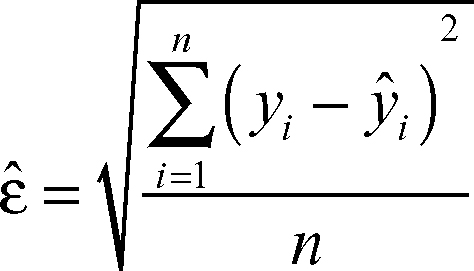stima
stima
stima in statistica, assegnazione sulla base dei dati campionari di uno o più valori numerici a un parametro ignoto, solitamente indicato con θ, che caratterizza una popolazione (per esempio, la statura media della popolazione italiana in un dato periodo). Nell’inferenza statistica si distingue tra i valori della popolazione (detti appunto parametri) e i corrispondenti valori numerici che si ricavano dal campione (che rappresentano le stime dei parametri stessi). Quindi, sulla base di un campione casuale si vuole trovare un valore, o un insieme di valori, per θ che sia la migliore approssimazione possibile del valore incognito della popolazione. Quando è assegnato un unico valore si parla di stima puntuale; se è assegnato un insieme di valori, si parla di stima per intervallo. In tali casi si cerca di stimare a quale intervallo appartiene, con una probabilità solitamente molto elevata (95%), il parametro cercato (→ confidenza intervallo di; → significatività).
Compiti della teoria della stima sono la individuazione di metodi di stima e la definizione di proprietà che essi devono possedere e che devono guidare nella scelta della stima migliore. I metodi più impiegati sono: il metodo dei momenti (→ momento), che consiste nello stimare i momenti di una popolazione con gli analoghi momenti campionari; il metodo della massima → verosimiglianza, consistente nello scegliere come stima del parametro il valore più verosimile, cioè quello che con maggior verosimiglianza avrebbe dato il risultato campionario ottenuto; il metodo dei → minimi quadrati, usato per la stima dei parametri di una funzione, che lega una variabile dipendente a una o più variabili indipendenti e consistente nell’assumere come stima dei parametri i valori che rendono minima la somma dei quadrati delle differenze fra i valori osservati della variabile dipendente e quelli risultati dalla funzione stimata. Qualunque sia il metodo impiegato, la stima ottenuta dipende dai dati campionari e varia solitamente con essi.
I metodi di stima possono essere applicati anche per stimare i parametri di un modello di → regressione e, in particolare, la componente casuale di tale modello. Nello specifico, gli scostamenti tra le osservazioni e le ordinate dei punti della retta di regressione (yi − ŷi) rappresentano una misura dell’errore di previsione e una stima dell’errore è data dallo scostamento quadratico medio tra queste due quantità:
Più in generale e in diversi ambiti della matematica si parla di stima dal basso (rispettivamente stima dall’alto) in presenza di una disuguaglianza in cui si minora (rispettivamente maggiora) una data quantità.