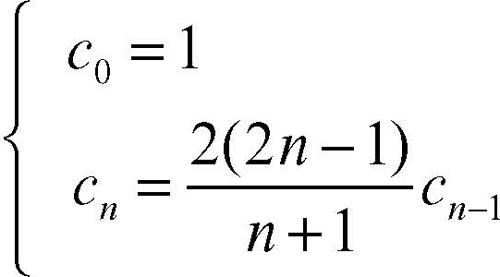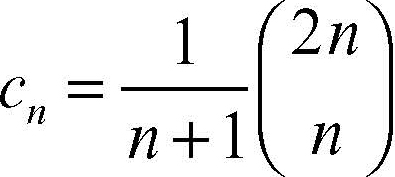Catalan, successione di

Catalan, successione di

Catalan, successione di successione numerica così definita per ricorrenza:

In modo equivalente la successione è definita dalla formula:

dove

indica il coefficiente binomiale.

I primi dieci numeri della successione sono: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862. Il numero c_n−1 fornisce la risposta al seguente problema: dato un prodotto di n fattori in un dato ordine, x₁ · x₂ · … · x_n, in quanti modi possono essere disposte le parentesi affinché siano indicate differenti priorità di moltiplicazioni tra due fattori adiacenti? Per esempio, dato il prodotto ordinato di 4 fattori, a, b, c, d, si hanno le seguenti c₄₋₁ = c₃ = 5 possibilità: ((ab)c)d; (a(bc))d; a((bc)d); a(b(cd)); (ab)(cd). La formula appare in molti problemi di combinatoria: il problema precedente può per esempio essere riformulato in termini di teoria dei grafi chiedendosi quanti diversi alberi binari possono essere costruiti con 4 nodi terminali in un dato ordine.