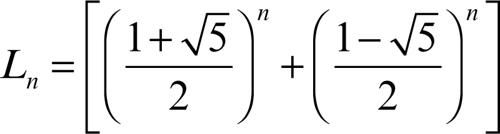Lucas, successione di
Lucas, successione di
Lucas, successione di successione i cui termini, indicati con Ln (detti numeri di Lucas), sono definiti dall’equazione alle differenze Ln = Ln−1 + Ln−2 a partire dalle condizioni iniziali L0 = 2, L1 = 1. I primi numeri di Lucas sono dunque 2, 1, 3, 4, 7, 11, 18, 29, 47, 78 ecc. L’espressione generale di Ln è data da
Per n → ∞ il rapporto Ln+1/Ln tende al numero aureo
perchè l’equazione alle differenze è la stessa dei numeri di Fibonacci Fn (→ Fibonacci, successione di). Tra le due successioni vale la relazione F2n = Fn ⋅ Ln; si ha inoltre L2n = Ln 2 − 2(−1)n, relazione che permette di calcolare rapidamente i numeri di Lucas di indice n = 2k, utili nella verifica della primalità dei numeri di Mersenne (→ Mersenne, successione di).