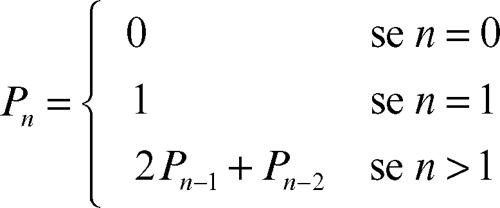Pell, successione di
Pell, successione di
Pell, successione di successione di numeri interi definita per ricorrenza a partire dai suoi primi due termini mediante la formula
L’n-esimo termine di tale successione è detto n-esimo numero di Pell; i primi numeri di Pell sono 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741. I numeri di Pell sono noti sin dall’antichità e nascono in relazione alla ricerca di buone approssimazioni razionali di √(2). Data infatti l’equazione diofantea (detta equazione di Pell) x 2 − 2y 2 = ±1, per ogni naturale n, le coppie di numeri interi (Pn−1 + Pn, Pn) risolvono tale equazione. Segue da ciò che, per n grande, il numero razionale (Pn−1 + Pn)/Pn fornisce una buona approssimazione razionale di √(2). Tali approssimazioni coincidono con quelle ottenibili a partire dalla successione delle ridotte dello sviluppo in frazione continua di √(2) e forniscono quindi le migliori approssimazioni razionali di tale numero. Più in generale è detta equazione di Pell ogni equazione diofantea del tipo x 2 − dy 2 =±1 dove d > 0 è un qualsiasi numero intero non quadrato perfetto.