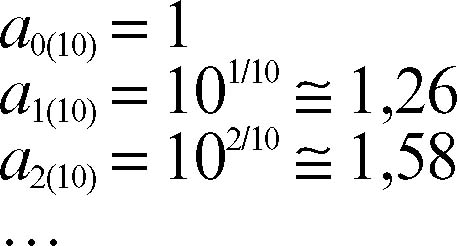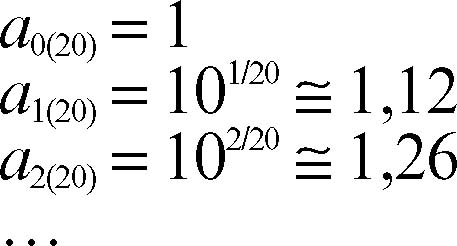Renard, successione di
Renard, successione di
Renard, successione di successione numerica finita {an(k)} formata da elementi in progressione geometrica, il cui primo elemento è 1 e l’ultimo è 10. Il termine an(k) della successione differisce dal precedente an−1(k) per un fattore uguale alla radice k-esima di 10. Quindi il termine an(k) della successione di Renard di ordine k è 10n/k. Per esempio, per k = 10 i termini della successione sono i seguenti:
L’ultimo termine è a10(10) = 1010/10 = 10. Se si sceglie k = 20, la successione è la seguente:
L’ultimo termine, il (20 + 1)-esimo, è a20(20) = 1020/20 = 10. Caratteristica di questa successione è che i prodotti, i quozienti, le potenze intere positive e negative di tali numeri sono ancora numeri di Renard. La successione fu introdotta intorno al 1870 dal colonnello francese Charles Renard (1847-1905), ed è utilizzata in problemi di meccanica applicata.