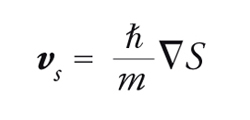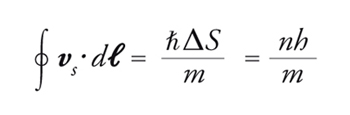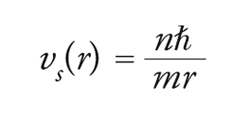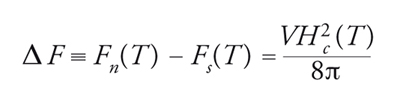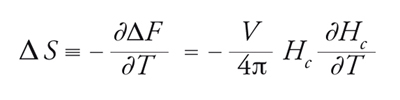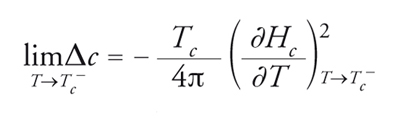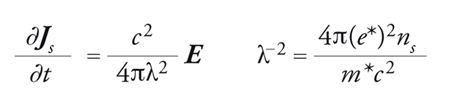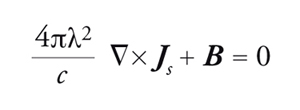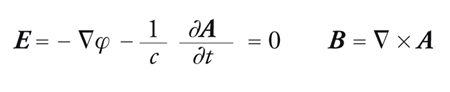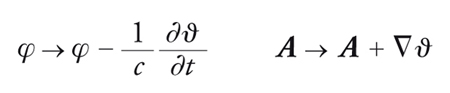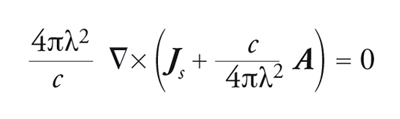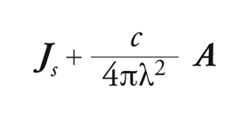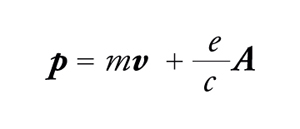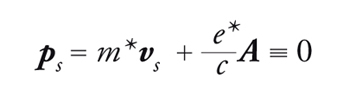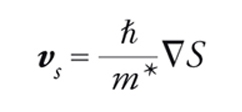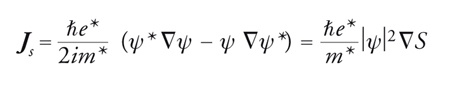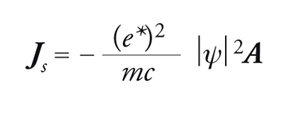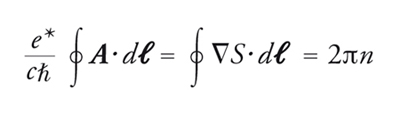Superconduttivita e superfluidita

Superconduttività e superfluidità

La superfluidità è il fenomeno per cui alcuni sistemi presentano viscosità nulla e possono quindi fluire senza dissipare energia. La superfluidità si manifesta per velocità di flusso e temperature inferiori a determinati valori critici, specifici di ciascun sistema. Partendo dall'osservazione sperimentale di anomalie nelle proprietà termodinamiche e di trasporto, si scoprì che l'elio liquido con numero isotopico 4 (⁴He) diventa superfluido (elio II) alla temperatura critica T_λ=2,17 K. La superfluidità dell'elio con numero isotopico 3 (³He) si manifesta a temperature molto più basse e fu scoperta solo nel 1971, perché il raggiungimento di temperature così basse richiedeva l'impiego di tecnologie più avanzate. La transizione, vicino alla curva di coesistenza con la fase solida, avviene alla temperatura critica T_c=2,7 mK.

All'assenza di viscosità nei superfluidi corrisponde l'assenza di resistenza elettrica per il moto degli elettroni di molti metalli, al di sotto di temperature critiche con valori tipici T_c≈1÷10 K, che risultano inversamente proporzionali alla radice della massa isotopica degli ioni che costituiscono il reticolo cristallino (effetto isotopico). Il fenomeno, detto superconduttività, fu scoperto da Heike Kamerlingh Onnes nel mercurio, con T_c=4 K. Temperature critiche più elevate sono state ottenute in leghe metalliche e successivamente in alcuni ossidi di rame che, normalmente isolanti, presentano il fenomeno della superconduttività ad alta temperatura (T_c≈30÷150 K) se opportunamente trattati. Lo stato superconduttivo, oltre che dalla resistenza elettrica nulla, è caratterizzato dall'espulsione del campo magnetico: il campo d'induzione magnetica B all'interno d'un superconduttore immerso in un campo magnetico H, d'intensità inferiore a un valore critico H_c, è nullo (effetto Meissner-Ochsenfeld).

L'elio è il più semplice elemento dopo l'idrogeno e presenta un'interessante varietà di comportamenti a bassa temperatura. A causa della piccola massa e della debolezza della parte attrattiva dell'interazione di van der Waals tra gli atomi, con diametro d=2,7 Å, l'He condensa nella fase liquida a temperature molto basse (l'⁴He è liquido al di sotto di 4,2 K) ed è l'unico elemento che resta liquido fino alle più basse temperature raggiunte e solidifica solo sotto alte pressioni. I due isotopi ³He ed ⁴He hanno comportamenti molto diversi che non possono essere ricondotti alla sola differenza di massa isotopica. Infatti, l'³He ha spin semintero e obbedisce, come gli elettroni, alla statistica di Fermi-Dirac: ogni stato quantistico di particella singola può essere occupato al più da una sola particella (principio d'esclusione di Pauli). L'⁴He, invece, ha spin zero e obbedisce alla statistica di Bose-Einstein: ogni stato quantistico può essere occupato da un numero arbitrario di particelle e ciò può dar luogo, in opportune condizioni, alla condensazione di Bose-Einstein. In questo caso, si ha un'occupazione macroscopica d'uno stato di particella singola.

Per comprendere la superfluidità e la superconduttività dobbiamo dapprima spiegare perché i rispettivi stati di flusso siano stabili (o meglio metastabili su tempi estremamente lunghi), anche se, per esempio nell'He, le interazioni tra gli atomi del liquido e le pareti del tubo in cui avviene il flusso sono più intense delle forze intermolecolari e dovrebbero tendere a frenare il moto ordinato. Deve esistere un meccanismo che impedisce il processo viscoso o resistivo, ossia la conversione dell'energia cinetica, associata al moto ordinato del fluido, in energia termica del moto disordinato dei singoli costituenti. Nel 1941 Lev Davidovič Landau stabilì un criterio di superfluidità sotto l'ipotesi che i sistemi in questione potessero scambiare energia con l'esterno solo attraverso la creazione o la distruzione d'eccitazioni elementari (quasi particelle) con energia ε e quantità di moto p ben definite e legate tra loro da una determinata relazione ε=ε(p) (legge di dispersione), specifica di ciascun sistema. Nei liquidi isotropi l'energia delle eccitazioni dipende solo dal modulo della quantità di moto p≡|p|. Le leggi di conservazione d'energia e quantità di moto associate alla possibilità d'eccitazione delle quasi particelle implicano che il moto del fluido possa essere attenuato solo se la velocità del flusso è maggiore d'una velocità critica v_c = [ε(p)/p]_min cioè pari al minimo della funzione ε(p)/p sulla curva di dispersione di quasi particella. L'esistenza d'un valore minimo non nullo costituisce una condizione necessaria di superfluidità. Un sistema gassoso non può essere un modello di superfluido, in quanto per lo spettro d'eccitazione di particella singola ε(p)=p²/2m, si ha v_c=0, dove m è la massa delle particelle.

Fenomenologia dell'4He

Cominciamo a discutere la superfluidità dell'⁴He, perché in questo caso la corrispondenza tra fenomenologia e interpretazione teorica è più diretta. Per molto tempo, l'⁴He è stato l'unico elemento atomico per cui si è sperimentalmente dimostrata la condensazione di Bose-Einstein e la conseguente superfluidità. Tuttavia, di recente nuove tecniche di raffreddamento, fino ai nK, e d'intrappolamento di atomi, hanno permesso di studiare il fenomeno della condensazione in gas rarefatti di atomi alcalini (agli inizi, nel 1995, solo Na e Rb). Ma dopo la scoperta iniziale, il campo si è espanso enormemente grazie all'individuazione dei vari aspetti del comportamento quantistico macroscopico di questi atomi intrappolati. Diverse questioni fondamentali sono state studiate e risolte in questi sistemi, in cui grandezze quali la densità e l'interazione interatomica sono direttamente manipolabili. Lo stato condensato, tuttavia, è metastabile e richiede bassissima densità per evitare la formazione d'aggregati. L'⁴He resta dunque il sistema principe per lo studio e la comprensione della condensazione e della superfluidità a densità ordinarie e per sistemi estesi.

Il calore specifico dell'⁴He aumenta quando la temperatura si avvicina al valore critico per la transizione superfluida, acquistando la forma peculiare della lettera greca λ, da cui la denominazione T_λ per la temperatura critica. Al punto critico, il calore specifico tende a divergere debolmente con l'andamento proprio delle transizioni di fase disordine-ordine di seconda specie: scendendo al di sotto della temperatura T_λ il sistema si ordina. Infatti, dall'andamento della curva di coesistenza tra il liquido superfluido e il solido, in base all'equazione di Clausius-Clapeyron, si deduce che l'entropia del superfluido è circa la stessa di quella del solido. L'interpretazione probabilistica dell'entropia suggerisce, quindi, che il liquido superfluido è ordinato quanto il solido. Tuttavia, quest'ordine non si forma nello spazio ordinario come per il solido, perché esperimenti di diffusione di raggi X non mostrano differenze tra la struttura della fase liquida sopra T_λ e quella della fase superfluida sotto T_λ. I valori della viscosità dinamica η dell'⁴He al di sotto di T_λ, misurati in esperimenti di flusso attraverso tubi capillari sottili (η〈10⁻¹¹ poise = 10⁻¹² Pa·s), sono almeno un milione di volte più piccoli di quelli misurati dallo smorzamento delle oscillazioni di un pendolo di torsione immerso nel liquido (η≈10⁻⁵ poise). Quest'enorme differenza, insieme a tante altre evidenze sperimentali, ha portato, nel 1940, alla proposta del modello a due fluidi di László Tisza, secondo il quale il liquido è costituito da due componenti compenetrantisi, di cui quella detta normale è viscosa e portatrice d'entropia, mentre quella superfluida è non viscosa, con entropia nulla e quindi altamente ordinata. Nel tubo capillare passa solo la componente superfluida e si misura, quindi, una viscosità bassissima; con il pendolo di torsione, invece, si misura la viscosità della componente normale. La densità ϱ_n della componente normale aumenta fino a coincidere con la densità totale ϱ a T_λ. Viceversa, la densità del superfluido ϱ_s si annulla al punto critico e coincide con la densità totale a T=0 K. La superfluidità è, dunque, caratterizzata da: (a) ordine a lungo raggio di tipo non spaziale; (b) eccitazioni elementari che soddisfano il criterio di Landau. Per quanto riguarda il punto (a), se potessimo considerare l'⁴He in prima approssimazione come un gas di bosoni non interagenti, a seguito della condensazione di Bose-Einstein avremmo un'occupazione macroscopica di uno stato di particella singola a temperature inferiori a un valore critico T_c che dipende solo dalla densità. A T=0 K tutte le particelle sarebbero nel condensato. A questo punto sarebbe naturale seguire il suggerimento di Fritz London e identificare la componente superfluida dell'⁴He sotto T_λ con la frazione di particelle nel condensato che si annulla alla temperatura critica, anche se in modo diverso da ϱ_s. Per di più, inserendo la densità dell'⁴He nella formula per la temperatura critica d'un gas di Bose, si ottiene T_c=3,4 K, non lontano, data la semplicità del modello, dal valore sperimentale di T_λ. La condensazione di Bose-Einstein promuoverebbe così l'ordinamento del sistema nello spazio delle quantità di moto e non nello spazio ordinario, in accordo con le evidenze sperimentali. Tuttavia, come si è detto, un gas di Bose non è un modello di superfluido perché non soddisfa il criterio di Landau. È quindi necessario tener conto dell'interazione tra le particelle oltre che della loro statistica. Lo stato fondamentale degli atomi di ⁴He interagenti deve produrre eccitazioni di quasi particelle compatibili con il criterio di Landau e, allo stesso tempo, dar luogo alla condensazione di Bose-Einstein. Quest'ultimo concetto deve essere, però, generalizzato al caso di particelle interagenti, in cui non è evidente il significato d'attribuire al concetto di stato di particella singola. Questa generalizzazione fu realizzata da Oliver Penrose nel 1951, riferendosi alla matrice densità di particella singola, i cui autovalori, per il gas, coincidono con i numeri di occupazione negli stati a quantità di moto fissata: si ha condensazione se esiste un autovalore macroscopico di tale matrice.

L'ordine che si realizza nella fase superfluida è rappresentato dalla comparsa dell'autovalore macroscopico. Il parametro d'ordine che Landau introdusse negli anni Trenta per caratterizzare le transizioni di fase disordine-ordine di seconda specie è dato, in questo caso, dall'autofunzione associata a tale autovalore, ossia da una funzione d'onda di particella singola occupata macroscopicamente.

Per quanto riguarda il punto (b) sul criterio di superfluidità di Landau, lo spettro dell'eccitazioni dell'⁴He è stato determinato sperimentalmente mediante diffusione di neutroni. A bassa energia esistono solo eccitazioni con grandi lunghezze d'onda λ, associate alla propagazione del suono nel liquido. I quanti di suono (fononi) hanno uno spettro ε(p)=up, con velocità del suono u e quantità di moto p=h/λ, dove h è la costante di Planck. Nikolaj Nikolaevič Bogoljubov nel 1947 aveva trattato un gas di bosoni rarefatto debolmente interagente, trovando questo spettro per le eccitazioni di bassa energia rispetto allo stato fondamentale condensato. Tuttavia, aumentando p, lo spettro sperimentale ε(p) passa attraverso un massimo per raggiungere una zona, detta zona rotonica, intorno a un valore di minimo locale Δ₀ (gap rotonica), per quantità di moto p₀≈ℏ/d_, dove d_ è la distanza interatomica media e ℏ=h/2π. Questo spettro delle eccitazioni di quasi particelle per l'⁴He superfluido era stato previsto da Landau, prima che fosse determinato sperimentalmente, a partire dall'andamento del calore specifico con la temperatura: c_v∼T³ (e non ∼T^3/2 come risulta per un gas di Bose) per basse temperature, è il comportamento proprio di un gas di fononi, mentre la comparsa di un termine esponenziale di tipo boltzmanniano a temperature più alte è dovuta alla popolazione di stati al di sopra del gap rotonico. Richard P. Feynman aveva derivato, negli anni 1953-1954, lo stesso spettro sotto l'ipotesi che le eccitazioni di un sistema di bosoni interagenti fossero associate a fluttuazioni di densità con una frequenza d'eccitazione fissata per ogni quantità di moto p, a partire da uno stato fondamentale con condensazione. Landau stesso, nel 1947, superò, inoltre, il paradosso dei due fluidi reciprocamente compenetrantisi, costituiti l'uno dalle particelle nel condensato (superfluido) e l'altro dalla frazione restante (normale), individuando nelle quasi particelle le molecole eccitate di Tisza. Landau mise in corrispondenza la componente normale con il gas di quasi particelle presenti a temperatura finita come eccitazioni spontanee del sistema e la componente superfluida con il substrato atomico o, meglio, con lo stato fondamentale di cui le quasi particelle costituiscono le eccitazioni, senza più distinguere tra i singoli atomi di ⁴He. Lo spettro sperimentale soddisfa il criterio di Landau con il valore di v_c dato dalla pendenza della tangente alla curva ε(p) passante per l'origine: si trova v_c≈60 m/s. Tale valore, però, è molto più alto del valore sperimentale, che è caratteristico di altri tipi di eccitazioni, associate al moto vorticale del sistema, del quale tratteremo nella sezione seguente, nell'ambito della proprietà di coerenza macroscopica dell'⁴He.

Coerenza quantistica su scala macroscopica nell'4He

Come abbiamo visto, il parametro d'ordine è una funzione d'onda di particella singola ψ=∣ψ∣exp(iS) che attraverso il fenomeno di condensazione descrive il comportamento globale del superfluido. In base ai principî generali della meccanica quantistica la fase S della funzione d'onda coincide con il potenziale di velocità, per cui la velocità del superfluido è

[1] formula.

A causa dell'occupazione macroscopica dello stato corrispondente, il modulo quadro della funzione d'onda descrive la densità vera e propria piuttosto che una densità di probabilità. Tuttavia nell'⁴He la relazione tra la densità di superfluido ϱ_s e la densità di condensato ∣ψ∣² è complicata a causa delle forti interazioni.

Avendo associato la transizione al punto T_λ con la comparsa del condensato e avendo considerato la fase della funzione d'onda del condensato come una variabile macroscopica, si manifestano effetti quantistici su scala macroscopica, come la quantizzazione della circuitazione della velocità. La funzione d'onda, infatti, deve essere in ogni punto univocamente definita e, quindi, la variazione della fase lungo un percorso chiuso deve essere un multiplo di 2π, cioè ΔS=2πn. Calcolando l'integrale di linea di v_s lungo un percorso chiuso, ossia la circuitazione del campo di velocità, la [1] può dar luogo a una circuitazione finita anche se il suo rotore è nullo (il rotore d'un gradiente è identicamente nullo). Usando l'epressione [1] si trova, infatti, per la circuitazione

[2] formula,

che risulta quantizzata in unità h/m, come verificato sperimentalmente. Ponendo in rotazione un contenitore cilindrico contenente elio a temperatura inferiore a T_λ intorno all'asse di simmetria, al disopra di un valore critico della velocità di rotazione, il superfluido acquista una velocità che dipende solo dalla distanza r dall'asse di rotazione; la [2] è soddisfatta se assumiamo un campo di velocità con componente tangenziale

[3] formula.

Infatti, in tal caso, in coordinate polari (r,φ), dℓ=rdφ coincide con l'arco di circonferenza a distanza r dall'asse di rotazione e la velocità è tangente all'arco stesso; v_s è singolare in r=0, dando luogo a linee vorticali con momento angolare quantizzato in unità ℏ. Il termine cinetico v_s² associato a questa velocità singolare divergerebbe, se la densità del superfluido non si annullasse nel punto di singolarità. Al nucleo delle linee vorticali è quindi associata la componente normale del liquido. Chiudendo su se stesse le linee vorticali, si possono generare gli anelli vorticali, eccitazioni del sistema dotate d'energia e di quantità di moto ben definite che, usate nel criterio di Landau, danno valori della velocità critica molto più vicini al valore sperimentale di quanto non si ottenga in base al solo spettro fononico-rotonico.

Fenomenologia dei superconduttori tradizionali

In modo analogo a quanto fatto per l'⁴He, procediamo in questo paragrafo a un'analisi della fenomenologia dei superconduttori che ci permetterà di determinare i requisiti generali di una teoria della superconduttività e in particolare come, anche per gli elettroni, possa realizzarsi la condensazione. La persistenza di correnti elettriche indotte in anelli superconduttori permette di stabilire un limite inferiore assai elevato per la conducibilità elettrica σ che può essere estrapolato all'infinito. In tal caso, in base alla legge di Ohm e alle equazioni di Maxwell per l'elettromagnetismo, segue che all'interno di un superconduttore il campo elettrico E è nullo e il campo d'induzione magnetica B è costante. L'effetto Meissner-Ochsenfeld mostra che il valore costante di B è B=0 indipendentemente dall'ordine con cui si eseguono i processi d'inclusione del campo magnetico e di raffreddamento sotto T_c per raggiungere lo stato finale. Per una categoria di superconduttori, detti di prima specie, B è nullo fino a un valore critico H_c del campo magnetico esterno, al di sopra del quale il sistema ridiventa normale; H_c è funzione della temperatura e si annulla al punto critico con pendenza finita e negativa: (dH_c/dT)_T=Tc〈0. In realtà, sia il cam-po elettrico che il campo magnetico, penetrano fino a una profondità λ, che, a T=0 K, è dell'ordine di qualche centinaio di Å: quando la temperatura si avvicina al valore critico a cui il sistema diventa normale, λ cresce secondo la legge

[4] λ ∼ (T_c − T)^−1/2

per T≲T_c. Al diminuire della temperatura, il calore specifico elettronico si annulla esponenzialmente piuttosto che seguire l'andamento lineare dei metalli normali. Come per i rotoni nell'⁴He, l'andamento esponenziale indica l'esistenza di un gap nello spettro d'eccitazioni. Quindi gli stati di energia più bassa risultano separati dallo stato fondamentale da un valore finito (gap) di energia Δ. Vari esperimenti, per esempio quelli di assorbimento di microonde, confermano l'esistenza di un gap che dipende dalla temperatura e si annulla alla temperatura critica con un andamento

[5] Δ∼ (T_c − T)^1/2

in prossimità di T_c. Uno spettro di eccitazioni con gap ha necessariamente un valore finito per il minimo di ε(p)/p e soddisfa quindi il criterio di superfluidità di Landau. L'andamento del calore specifico vicino a T_c è discontinuo. Ciò trova un riscontro immediato dal punto di vista teorico. In base all'effetto Meissner-Ochsenfeld, lo stato superconduttivo è indipendente dall'ordine con cui si realizza l'inclusione del campo e l'abbassamento della temperatura, per cui si possono applicare le leggi della termodinamica all'equilibrio. Per T〈T_c, dove è stabile la fase superconduttiva, l'energia libera del superconduttore F_s(T) a campo magnetico nullo è minore di quella, F_n(T), che il sistema avrebbe se fosse nella fase normale. La differenza deve essere compensata dall'energia magnetica associata al campo magnetico critico a quella temperatura, perché, per tale valore del campo, il sistema torna normale, ossia si ha

[6] formula,

dove V è il volume del superconduttore e abbiamo assunto la permeabilità magnetica del mezzo nello stato normale uguale a 1.

La differenza di entropia tra la fase normale e la fase superconduttiva è

[7] formula.

Da questo segue che ΔS è sempre positiva per T〈T_c (in quanto ∂H_c/∂T〈0) e si annulla a T=T_c, dove H_c=0. Il superconduttore è quindi più ordinato del metallo normale. La differenza nel calore specifico, che è data da Δc≡TV−∂ΔS/∂T , permane finita alla temperatura critica e assume il valore

[8] formula,

dato che H_c(T) ha pendenza finita per T→T_c−. La discontinuità del calore specifico è una proprietà caratteristica delle transizioni di fase disordine-ordine di seconda specie quando vengono trattate in approssimazione di campo medio.

Nei superconduttori dobbiamo individuare il tipo di ordinamento che si produce nel passare da sopra a sotto T_c. Come avviene per l'⁴He, esperimenti di diffusione di raggi X indicano che l'ordinamento non avviene nello spazio ordinario, dato che non si ha nessun cambiamento di configurazione spaziale degli elettroni. Saremmo portati a concludere che, anche nei superconduttori, il passaggio dalla fase normale a quella superconduttiva avviene con un ordinamento nello spazio delle quantità di moto, legato cioè a un fenomeno di condensazione, come risultato di una semplice teoria fenomenologica dovuta ai fratelli London (1933), che caratterizza i superconduttori e dà conto dell'effetto Meissner-Ochsenfeld.

Abbiamo caratterizzato un superconduttore ideale come un perfetto conduttore (σ=∞) e un perfetto diamagnete (B=0). La prima proprietà è assicurata da un moto privo d'attrito dei portatori di carica, la cui carica efficace e* sarà determinata nel seguito. L'inerzia dei portatori è caratterizzata da una generica massa efficace m*. L'equazione del moto è allora m*v∙_s=e*E, in cui il prodotto della massa per l'accelerazione è uguale alla forza esercitata dal campo elettrico E che agisce sulla carica e*. In termini della densità di corrente J_s=e*n_sv_s, l'equazione del moto diventa

[9] formula,

dove c è la velocità della luce nel vuoto e n_s è il numero di portatori di carica superconduttori per unità di volume; λ ha le dimensioni di una lunghezza e, come vedremo tra breve, coincide con la profondità di penetrazione del campo magnetico, introdotta in precedenza. Per descrivere la seconda proprietà dei superconduttori, cioè l'effetto Meissner-Ochsenfeld, i fratelli London postularono (in analogia con l'effetto pelle relativo alla penetrazione di un campo elettrico alternato in un conduttore) un'equazione aggiuntiva alle equazioni di Maxwell per l'elettromagnetismo

[10] formula.

Il prefattore è stato scelto in modo da rendere la [9] e la [10] compatibili con l'equazione di Maxwell c∇×E=−∂B/∂T. Eliminando la densità di corrente J_s dalla [10] con l'ausilio dell'equazione di Maxwell c∇×B=−4πJ_s, si trova l'equazione per il solo campo d'induzione magnetica

[11] ∇ × ∇ × B + λ²B = 0.

Risolvendo quest'equazione per un superconduttore seminfinito con un campo magnetico esterno applicato parallelamente alla superficie di separazione con il vuoto, si trova che il campo decade esponenzialmente all'interno del superconduttore in uno spessore λ, che coincide, quindi, con la profondità di penetrazione e l'effetto Meissner-Ochsenfeld risulta coerentemente descritto.

Il campo elettrico E e quello magnetico B sono in genere espressi attraverso un potenziale scalare φ e un potenziale vettore A mediante le relazioni:

[12] formula.

Senza cambiare i valori dei campi fisici, si possono cambiare i potenziali con una trasformazione, detta di gauge, caratterizzata da una funzione ϑ(r,t) arbitraria,

[13] formula.

In meccanica quantistica, sotto trasformazione di gauge, è necessario anche trasformare la funzione d'onda del sistema, ψ→exp(ieϑ/ℏc)ψ. Se esprimiamo B attraverso il potenziale vettore A, otteniamo che la [6] diventa

[14] formula.

Scegliamo una gauge per cui ∇∙A=0; in un superconduttore isolato dove non ci sono sorgenti di corrente e quindi anche ∇∙J_s=0, si ottiene che il vettore J_s+cA/(4πλ²), oltre ad avere rotore e divergenza nulli, ha componente normale alla superficie del campione nulla ed è perciò identicamente nullo. Questa caratterizzazione dell'effetto Meissner-Ochsenfeld comporta, quindi, una relazione precisa tra densità di corrente e potenziale vettore

[15] formula.

Ricordiamo che, in presenza di campo magnetico, le equazioni del moto implicano che la quantità di moto del singolo elettrone sia modificata in

[16] formula.

Considerando ora la quantità di moto associata alla supercorrente come valore medio associato al singolo portatore di carica, si ha

[17] formula,

secondo la [15]. Quindi, mentre in un metallo normale, in assenza di potenziale scalare, si annulla la corrente e la quantità di moto varia con A da punto a punto, in un superconduttore si annulla la quantità di moto e la corrente varia spazialmente con il potenziale vettore e scherma il campo esterno dando luogo all'effetto Meissner-Ochsenfeld. Se ne deduce che le equazioni fenomenologiche che schematizzano nelle linee essenziali il comportamento dei superconduttori implicano, almeno nelle condizioni poste, un ordine nello spazio delle quantità di moto con occupazione macroscopica di un singolo stato con quantità di moto totale nulla da parte dei portatori di carica.

In conclusione, sia la fase superfluida dell'⁴He sia la fase superconduttiva corrispondono a fasi ordinate con condensazione nello spazio delle quantità di moto. Gli elettroni, tuttavia, sono fermioni e, in base al principio di esclusione di Pauli, possono condensare solo se preventivamente formano stati legati a coppie che si comportano come pseudo bosoni con carica e*=2e e massa m*=2m. La distanza relativa tra i due elettroni legati in una coppia introduce nella descrizione un'ulteriore lunghezza caratteristica ξ, detta distanza di coerenza. In analogia con quanto detto per l'⁴He, il parametro d'ordine sarà l'autofunzione con autovalore macroscopico della matrice densità a due particelle, opportunamente pesata. Quest'interpretazione del parametro d'ordine come funzione d'onda dei portatori di carica superconduttori fu ipotizzata da Vitalij Lazarevič Ginzburg e Landau nel 1950, ancor prima della teoria microscopica della superconduttività e costituì la base della teoria fenomenologica della superconduttività vicino al punto critico.

Prima di trarre le conseguenze generali dell'esistenza di questo particolare parametro d'ordine associato alla funzione d'onda di coppie superconduttrici, ricordiamo che stati legati di coppia possono essere generati nei superconduttori tradizionali dall'interazione tra elettrone e oscillazioni del reticolo: un elettrone in moto distorce il reticolo e un secondo elettrone a una certa distanza dal primo può risentire di tale distorsione. In particolare, se le fluttuazioni di carica del reticolo dovute alla distorsione sono tali da schermare positivamente il primo elettrone, il secondo elettrone sarà attratto dal primo con il risultato netto di un'interazione efficace attrattiva tra i due elettroni. Leon N. Cooper mostrò, nel 1956, che un'interazione efficace attrattiva comunque debole conduce a un'instabilità della superficie di Fermi con formazione di stati legati di coppie di elettroni con quantità di moto e momento angolare orbitale nulli e spin opposto, dette coppie di Cooper. John Bardeen, Cooper e J. Robert Schrieffer individuarono la struttura dello stato fondamentale di un sistema di N fermioni legati in coppie di Cooper che condensano (teoria BCS, 1957) e calcolarono tutte le grandezze fisiche caratteristiche di questo stato. In particolare, la temperatura critica è in accordo con l'effetto isotopico e l'andamento del gap di eccitazione dallo stato fondamentale è in ottimo accordo con i dati sperimentali. La funzione d'onda relativa a tali coppie, proporzionale al parametro d'ordine sopra introdotto, nella teoria BCS è a sua volta proporzionale al gap superconduttivo, dando ragione del comportamento del gap al variare della temperatura vicino al punto critico, dato dall'espressione [5], che è caratteristico del parametro d'ordine per le transizioni di fase di seconda specie in approssimazione di campo medio.

Invece di seguire la formulazione più complicata della teoria microscopica BCS, utilizzereremo nella prossima sezione la formulazione fenomenologica basata sulla funzione d'onda delle coppie, per ricavare le proprietà dei superconduttori.

Coerenza quantistica su scala macroscopica nei superconduttori

Il flusso della supercorrente, come per l'⁴He, si associa al gradiente della fase della funzione d'onda del condensato di coppie di Cooper

[18] formula,

calcolata nel centro di massa della coppia r=(r₁+r₂)/2, dove r₁e r₂ sono i raggi vettori che determinano la posizione dei due elettroni.

Tenendo conto della normalizzazione della funzione d'onda del condensato e ponendo il parametro d'ordine ψ(r)=^∣ψ^∣exp(iS), la densità di corrente superconduttiva è data da:

[19] formula.

In presenza di un campo magnetico (espresso mediante il potenziale vettore A definito nella [12]) la densità di corrente diventa

e* ℏ e*

[20] J_s = ____{ψ* (__ ∇ − __ A)ψ +

2m* i c

ℏ e* ℏ e*

+[(__ ∇ − __ A)ψ]*ψ} = ___ ^∣ψ^2∣(∇S − ___ A)..

i c m* cℏ

Se si assume (come proposero fenomenologicamente i London) che la funzione d'onda non cambia in presenza di campo magnetico esterno [ψ(A≠0)=ψ(A=0)] e, poiché in assenza di campo esterno un superconduttore isolato ha correnti nulle al suo interno 〈ψ(A)^∣v_s^∣ψ(A)〉=〈ψ(0)^∣v_s^∣ψ(0)〉=0, si ottiene che

[21] formula.

La stessa equazione si può ricavare considerando che in un superconduttore isolato non ci può essere una sorgente di corrente, per cui ∇∙J_s=0. Con una scelta opportuna della gauge [13] si può sempre porre ∇∙A=0, per cui, in base alla [20], la fase S soddisfa l'equazione ∇²S=0 ed è perciò costante su tutto il campione. In tal caso, il gradiente della fase si annulla e la relazione tra corrente e potenziale si riduce alla [21]. Questa è analoga alla relazione [15] della teoria fenomenologica dei London, vista precedentemente, che dava conto dell'effetto Meissner-Ochsenfeld, purché, come abbiamo già detto, il parametro d'ordine sia normalizzato in modo che ^∣ψ^∣2=n_s. Questa rigidità della funzione d'onda (in particolare della sua fase S), che non risponde all'introduzione del campo esterno, è un tratto distintivo della superconduttività e dà un fondamento microscopico alla relazione [21] da cui discende l'effetto Meissner-Ochsenfeld. La profondità di penetrazione λ, data dalla [9], è ora espressa in termini del modulo quadrato del parametro d'ordine. Dato l'andamento sperimentale di Δ in funzione della temperatura vicino a T_c ([3]), si ha una conferma ulteriore che il parametro d'ordine è stato scelto in modo appropriato e che la transizione superconduttiva è ben descritta dalla relazione n_s∼T_c −T, valida in approssimazione di campo medio.

Anche per i superconduttori la funzione d'onda del condensato deve essere a un solo valore e quindi la circuitazione del gradiente della fase deve essere, come per l'⁴He, un multiplo di 2π. In presenza di campo magnetico, se scegliamo il percorso ben all'interno del superconduttore, dove la corrente è nulla (la corrente circola solo in uno strato superficiale di spessore λ), in base alla [20] si ha

[22] formula.

Ricordando la relazione matematica per cui la circuitazione di un vettore è uguale al flusso del suo rotore, si ha che nei superconduttori il flusso del campo magnetico Φ(H) risulta quantizzato in unità hc/e*: questo risultato è l'analogo della quantizzazione della circuitazione della velocità nell'⁴He superfluido e comporta l'annullamento del parametro d'ordine nel nucleo della linea di vortice. La verifica sperimentale della quantizzazione del flusso ha mostrato che la carica efficace e* è il doppio della carica elettronica, in perfetto accordo con l'idea della formazione di coppie che condensano. London, con un argomento analogo a quello dato, aveva previsto la quantizzazione del flusso, ma con carica pari a quella dell'elettrone.

Fin qui abbiamo assunto implicitamente che la distanza ξ su cui varia la funzione d'onda del condensato sia molto maggiore della profondità di penetrazione λ del campo magnetico. Questo implica che sia svantaggioso creare variazioni locali della fase S su distanze d'ordine λ e creare singoli quanti di flusso. L'espulsione del campo magnetico sarà quindi totale fino a un valore critico del campo (effetto Meissner-Ochsenfeld completo, superconduttori di tipo I). In molti superconduttori (tipo II; a questo tipo appartengono, per es., tutti i superconduttori ad alta temperatura critica descritti nella prossima sezione) si verifica la condizione opposta, il che rende negativa l'energia di creazione di una superficie che separa lo stato normale dallo stato superconduttore. Al di sopra di un campo critico H_c1 (analogo al valore critico della velocità di rotazione per la comparsa dei vortici nell'elio superfluido), diventa allora vantaggiosa la penetrazione parziale del campo magnetico sotto forma di filamenti con parametro d'ordine nullo, che portano ciascuno un quanto di flusso (vortici). Questi filamenti si dispongono secondo una geometria reticolare che dipende dalle caratteristiche dell'interazione tra i singoli vortici, come fu dimostrato da Aleksej Alekseevič Abrikosov nel 1952.

Poiché la funzione d'onda di un superconduttore isolato è caratterizzata da una fase macroscopica, se realizziamo una giunzione fra due superconduttori, separati da un sottile strato isolante di spessore d, si genererà un accoppiamento tra i due superconduttori con un'energia funzione periodica della differenza delle due fasi ∼cos(S₂−S₁), con S₂−S₁ ∼d ^∣∇S^∣. In base alla sostituzione minimale [16], la derivata dell'energia rispetto al gradiente della fase dà la corrente. Si può quindi creare una supercorrente attraverso la giunzione anche in assenza di differenza di potenziale, in quanto le coppie possono passare da un lato all'altro della giunzione. Sfruttando l'invarianza di gauge si dimostra facilmente che la presenza di una differenza di potenziale costante Δφ=V tra i capi della giunzione dà luogo a una variazione aggiuntiva della differenza di fase ∼Vt e quindi a una corrente alternata con frequenza pari a S∙=−e*V/h. I fenomeni di quantizzazione e d'interferenza alla base di questo e di altri effetti, osservati sperimentalmente nelle più diverse circostanze, sono strettamente legati alle variazioni della fase della funzione d'onda del condensato e costituiscono l'esempio più evidente del manifestarsi di fenomeni quantistici su scala macroscopica.

Superconduttori ad alta temperatura

È chiaro che se si potessero realizzare superconduttori a temperatura ambiente diventerebbero più economiche e facilmente accessibili le applicazione tecnologiche basate sui superconduttori, come per esempio la trasmissione di energia elettrica senza perdite, o l'uso generalizzato di elettromagneti superconduttori. È quindi naturale che, nel corso dei decenni, si tentasse di trovare materiali superconduttori capaci di sostenere valori elevati di supercorrenti in presenza di forti campi magnetici e a temperature critiche elevate. Mentre la ricerca di materiali adatti alla realizzazione di magneti superconduttori aveva dato buoni risultati, la ricerca di materiali con alte temperature critiche era stata meno fruttuosa (il record era, fino al 1986, di 23 K in una lega di Nb-Ge scoperta nel 1973). La scoperta nel 1986 da parte di Johannes Georg Bednorz e Karl Alexander Müller di composti ossidi di rame e terre rare (cuprati) con temperature critiche superconduttive molto superiori a quelle dei composti tradizionali (il record attuale si aggira intorno ai 160 K) ha aperto scenari nuovi nel campo della superconduttività. Da un punto di vista pratico e applicativo è molto importante che T_c sia superiore alla temperatura di liquefazione dell'azoto liquido (77 K) perché il raffreddamento dei materiali diventa molto più semplice ed economico rispetto a quello ottenuto con l'elio, usato come refrigerante per i superconduttori tradizionali.

I cuprati si raggruppano in diverse famiglie, per esempio La_2−xSr_xCuO₄ (con 0≤x≲0,3 e T_c massima di circa 42 K per x≈0,15), YBa₂Cu₃O_6+x (con 0,6≤x≤1 e T_c massima di circa 92 K per x≈0,95), Bi₂Sr₂CaCu₂O_8+x (con T_c massima di circa 92 K per x≈0) e molte altre. Il record attuale è stato raggiunto in HgBa₂Ca₂Cu₃O_2−x, con una T_c massima di 164 K sotto pressione. Tutti questi sistemi hanno in comune una struttura piuttosto complessa, caratterizzata da piani debolmente accoppiati di atomi di rame circondati da atomi di ossigeno. Questo fatto conferisce alla struttura elettronica un carattere quasi bidimensionale. In assenza di drogaggio, la cella unitaria CuO₂ dei piani rame-ossigeno contiene una lacuna elettronica. In base alla teoria delle bande, quindi, il sistema dovrebbe essere metallico. Tuttavia, a causa della forte correlazione elettrone-elettrone, il sistema è isolante, le lacune sono localizzate e i loro spin sono ordinati antiferromagneticamente. La fase metallica (e quella superconduttiva per temperature inferiori a T_c) compaiono quando questi sistemi vengono drogati chimicamente, in modo da introdurre lacune aggiuntive (sostituendo, per es., il La con lo Sr) o elettroni nei piani rame-ossigeno. Nel caso di drogaggio con lacune le temperature critiche sono solitamente più elevate. Una forte anisotropia nella resistività, che sui piani rame-ossigeno è di ordini di grandezza più bassa che in direzione perpendicolare ai piani, indica che i piani rame-ossigeno sono le strutture rilevanti per i fenomeni di conduzione .

Tre sono le caratteristiche principali della fase metallica ottenuta sotto drogaggio: (a) nella fase normale (non superconduttiva) si hanno comportamenti anomali che deviano da quelli usuali della teoria di Landau dei liquidi di Fermi. Secondo questa teoria, le eccitazioni di bassa energia di un metallo sono ottenute sostituendo le particelle vere (elettroni o lacune fortemente interagenti) con un gas di quasiparticelle debolmente interagenti, anch'esse con statistica di Fermi-Dirac. Si può dimostrare che con un'accensione lenta dell'interazione, le particelle si rivestono dando luogo a quasiparticelle con alcuni parametri efficaci (come la massa efficace invece della massa vera). Le proprietà restano quelle di un gas debolmente interagente (superficie di Fermi, calore specifico per basse temperature lineare in temperatura, contributo elettronico alla resistività quadratico in temperatura). Questi comportamenti standard nei metalli sono violati nella fase normale dei cuprati: per esempio, intorno alla zona di drogaggio ottimale dove la T_c è massima, la resistività nei piani è lineare in temperatura da T_c fino alle temperature più elevate; (b) per drogaggi inferiori a quello ottimale si apre uno pseudogap (gap incompleto) nella struttura elettronica a temperature molto più elevate di T_c. Si ipotizza che questo pseudogap possa essere dovuto alla formazione di uno stato normale ordinato il cui carattere, al momento, resta elusivo. Alternativamente, lo pseudogap potrebbe essere dovuto alla formazione di coppie di Cooper senza coerenza di fase. La superconduttività comparirebbe a temperature più basse, quando le coppie quasibosoniche condensano. In questo caso la superconduttività ad alta temperatura sarebbe un fenomeno intermedio tra la condensazione di coppie di Cooper (come nella teoria BCS), in cui le coppie condensano non appena si formano, e la condensazione di Bose di bosoni preformatisi a temperature superiori a T_c; (c) il parametro d'ordine superconduttivo è associato a stati di coppia con momento angolare non nullo: il numero quantico associato è l=2 e pertanto si parla di coppia con simmetria di onda d.

Il meccanismo attrattivo che provoca la formazione di coppie resta al momento elusivo. C'è un consenso diffuso, favorito dal fatto che l'effetto isotopico sulla T_c in questi materiali è debole o assente, sul ruolo fondamentale giocato dalla forte correlazione elettrone-elettrone. Secondo una linea di pensiero, questa correlazione è responsabile di correlazioni magnetiche a corto raggio e della conseguente formazione di coppie di elettroni in stati di singoletto. Una possibilità alternativa è che la correlazione favorisca instabilità di vario genere (magnetiche, di ordinamento di carica, ecc.) in prossimità delle quali le forti fluttuazioni possono mediare l'accoppiamento tra gli elettroni. La successiva osservazione di effetti isotopici di vario genere (per es., sulla temperatura di formazione dello pseudogap) in questi sistemi ha rilanciato anche la possibilità che le fluttuazioni reticolari giochino un ruolo importante. Tuttavia al momento, è generalmente riconosciuto che, anche in questo ultimo caso, non si può prescindere dal considerare la forte correlazione elettrone-elettrone e le conseguenti anomalie dello stato normale come ingredienti essenziali della fisica di questi sistemi.

La novità delle problematiche relative a questi materiali è stata e sarà di stimolo per ripensare a fondo concetti fondamentali della fisica dello stato solido e, probabilmente, faciliterà la progettazione e la fabbricazione di nuovi materiali con temperature critiche più elevate e con requisiti più adatti alle applicazioni.

Fenomenologia dell'3He e formazione di coppie superfluide

Essendo gli atomi di ³He dei fermioni, questo sistema è l'esempio classico di un liquido normale di Fermi che obbedisce alla teoria di Landau. Studiando le proprietà magnetiche della fase solida lungo la curva di solidificazione, si scoprì nel 1972 che, nel liquido a campo magnetico nullo, si verifica una transizione di fase dal liquido normale a una prima fase superfluida (fase A) a T_A=2,7 mK, seguita da un'altra fase superfluida (fase B) a T_B=2,0 mK. A T_A si ha una discontinuità del calore specifico che, come già detto per i superconduttori, è propria delle transizioni di fase disordine-ordine di seconda specie quando la teoria di campo medio è valida, mentre a T_B si ha un picco molto stretto anch'esso indizio di transizione di fase di seconda specie. La superfluidità delle due fasi è stata dimostrata sperimentalmente con lo smorzamento delle oscillazioni di un filo percorso da corrente in campo magnetico trasverso. La densità della componente normale decresce rapidamente al di sotto di T_A. Lo stato legato di coppia, in questo caso, deve essere il risultato delle forze di van der Waals, che sono attrattive a grandi distanze, ma diventano fortemente repulsive tra atomi di ³He troppo vicini. Ciò dà luogo a una funzione d'onda che si annulla al tendere a zero della distanza tra gli atomi della coppia e impone un valore non nullo del momento angolare totale. Decomponendo l'interazione in onde parziali si trova attrazione per momento angolare l=1 (coppie con simmetria di onda p). Data l'antisimmetria spaziale della funzione d'onda di coppia, i due atomi di ³He si accoppiano nello stato di tripletto di spin (S=1).

Informazioni più specifiche si ottengono in presenza di un campo magnetico, con fenomeni che sono assenti negli altri superfluidi e caratterizzano l'³He come un superfluido magnetico. Il valore di T_B è ridotto quadraticamente con il campo magnetico, mentre per la fase A si ha uno sdoppiamento in due fasi con una separazione delle due temperature critiche ΔT_A centrata intorno al valore di T_A a campo nullo e lineare rispetto all'intensità del campo. La suscettività magnetica è indipendente dalla temperatura. Nella fase A è simile a quella del liquido normale, mentre nella fase B risulta ridotta.

Questi effetti sono dovuti alla presenza di coppie in stato di tripletto (coppie in stato di singoletto, come nei superconduttori, sono sempre distrutte dal campo magnetico). Nella transizione alla fase A si formano coppie in due dei tre possibili stati di tripletto. In campo magnetico, gli stati con proiezione di S concordi con il campo (preso lungo l'asse z) S_z=1 aumentano il loro numero e condensano a una T_A maggiore, mentre quelli con S_z=−1 sono ridotti e condensano a una T_A minore. Il passaggio dalla fase A alla fase B viene invece associato a un cambiamento verso uno stato di coppie che si formano in una miscela coerente delle tre componenti di spin del tripletto (S=±1,0).

Bibliografia

Barone, Paternò 1982: Barone, Antonio - Paternò, Gianfranco, Physics and applications of the Josephson effect, New York-Chichester, Wiley, 1982.

De Gennes 1966: de Gennes, Pierre-Gilles, Superconductivity of metals and alloys, New York, Benjamin, 1966.

Gorter 1940: Gorter, Cornelis J., Superconductivity until 1940 in Leiden and as seen from there, ‟Reviews of modern physics", 36, 1964, pp. 7-11.

London 1950-1954: London, Fritz, Superfluids, New York, Wiley, 1950-1954, 2 v.

Müller, Bednorz 1988: Müller, Karl A. - Bednorz, Johannes G., Perovskite-type oxides. The new approach to high-T_c superconductivity, ‟Reviews of modern physics", 60, 1988, pp. 585-600.

Schrieffer 1964: Schrieffer, J. Robert, Theory of superconductivity, Reading (Mass.), Benjamin, 1964.

Thomas 1990: Thomas, Harry, Some remarks on the history of superconductivity, in: Earlier and recent aspects of superconductivity: lectures from the international school, Erice, Trapani, Sicily, 1989, edited by Johannes G. Bednorz, Karl A. Müller, Berlin-New York, Springer, 1990, pp. 2-44.

Tilley, Tilley 1986: Tilley, David R. - Tilley, John, Superfluidity and superconductivity, 2. ed., Bristol, Hilger, 1986.