Cayley, tabella di

Cayley, tabella di

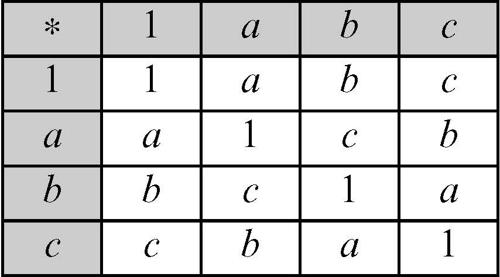
Cayley, tabella di tabella mediante la quale può essere definito un gruppo finito. Se G è un gruppo di ordine n con operazione ∗, allora la tabella di Cayley di G è la tabella moltiplicativa (di fatto la sua tavola pitagorica), con n + 1 righe e n + 1 colonne, nella quale vengono indicati tutti i prodotti tra gli elementi del gruppo come segue: si etichettano gli elementi del gruppo con i numeri da 1 a n, con la convenzione che g₁ sia l’elemento neutro, che si indica con 1, e quindi sia G = {1, g₂, …, g_n}. Dopo aver indicato l’operazione ∗ nella prima casella in alto a sinistra, si etichettano le restanti celle della prima colonna con tutti gli elementi di G nell’ordine fissato; similmente si etichettano le restanti celle sulla prima riga. Si scrivono dunque tutti i prodotti tra gli elementi di G, ponendo l’elemento g_i ∗ g_j all’incrocio della riga relativa all’elemento g_i (la (i + 1)-esima) con la colonna relativa all’elemento g_j (la (j + 1)-esima). Per esempio, se G è il gruppo di Klein, G = {1, a, b, c}, allora la sua tabella di Cayley è:

Per determinare l’inverso di un dato elemento di G posto sulla prima colonna, basta cercare sulla prima riga l’elemento in corrispondenza del quale si ha l’elemento neutro. Molte proprietà di un gruppo possono essere dedotte dalla sua tabella di Cayley: per esempio, se la tabella è simmetrica rispetto alla diagonale che va dall’angolo in alto a sinistra a quello in basso a destra, allora il gruppo è commutativo. La tabella di Cayley di un gruppo è un → quadrato latino.